刚性接触网悬挂结构刚度识别方法

2021-12-22张玲芳黄国君杨国伟程桂军纪占玲

铁道科学与工程学报 2021年11期

张玲芳，黄国君，杨国伟，程桂军，纪占玲

(1. 中国科学院力学研究所，北京 100190；2. 中国科学院大学工程科学学院，北京 100190)

刚性接触网-受电弓系统[1]是目前城市地铁主要受流方式，与柔性接触网相比，刚性接触网具有坚固耐用、运行安全、安装方便、防火性好、维护成本低、隧道净空要求低、抗风性能好等优点。刚性接触网已在我国广州、成都、上海、北京等地铁工程中得到广泛应用。在弓网关系的研究中[2-4]，模型的准确建立是十分重要的。一些建模参数如刚性接触网的密度、截面几何参数、杨氏模量和跨度等都易于获得。关金发等[5-6]研究发现：悬挂结构刚度对弓网受流质量会产生较大影响，是建立模型的重要结构参数。但是不同于其它结构参数，悬挂结构刚度的影响因素较多，包括支撑底座类型、悬挂结构的高度、刚性接触网与支座之间的连接位置等，不易直接获得。代洪宇等[6-8]利用能量守恒将悬挂结构等效成弹簧，建立刚性接触网模型，这是目前被广泛接受的力学简化模型(如图1)。BAUTISTA等[9]也提出了一种有限元刚性接触网模型和多体连杆受电弓模型的建模方式，但这些工作都未对所建模型进行验证。目前，弓网耦合的模型验证[10]主要基于2 个方法：一是参照标准EN50318[11]对弓网耦合仿真方法进行确认，但标准中给出的模型参数是柔性接触网，对刚性接触网模型的适用性有待考究。二是将弓网接触力的仿真结果与实车实验测量结果进行对比[12]，此种验证方法成本较高。此外，进行模型验证的文献也并未提及如果验证结果不好的情况下如何修正仿真模型。本文提出一种利用刚性接触网的固有频率识别悬挂结构刚度的方法，提供了一种测量实际刚性网悬挂刚度的方法。该问题属于结构动力学反问题的范畴，并应用遗传算法[13]求解，将从刚性接触网模态信息识别建模结构参数的反问题转化成参数寻优问题，识别到的刚度值可用于模型的修正和验证。此外，由于固有频率对悬挂结构刚度变化的敏感性，本方法还可用于悬挂结构的损伤识别。在损伤识别[14-15]方面，一般固有频率和阵型信息同时采用才能得到相对准确的结果，但是本方法能够仅使用刚性接触网的固有频率就能识别到悬挂结构弹簧的损伤位置，并能得到损伤后的弹簧刚度，这在很大程度上减少了模态实验的测点数量。

图1 传统的悬挂结构等效示意图Fig.1 Traditional equivalent method of suspension structure

1 刚度识别方法

1.1 力学原理

忽略阻尼时经有限元法离散后的刚性接触网自由振动控制方程见式(1)。

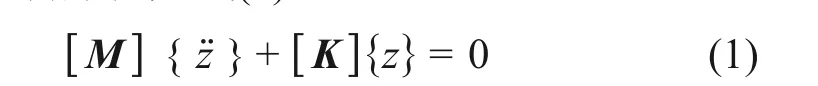
式中：[M]，[K]分别为有限单元的质量矩阵、刚度矩阵；{z}和{z¨ }为垂向位移和加速度。

将{z}写成振型坐标形式，可由式(1)得到式(2)：

其中：[Φ]为振型矩阵；[Ω]为频率矩阵。

式中：ωi为第i阶固有频率。

由式(2)和式(3)及振型向量的正交性可得：

式中：{Φi}为第i阶振型向量。

结构的模态特性ωi和{Φi}由结构的质量分布和刚度分布决定，这些结构特性分别由质量矩阵[M]和刚度矩阵[K]表征。通过结构特性进行理论模态分析得到模态特性ωi和{Φi}，这构成结构动力学正问题。由式(4)可见：悬挂结构刚度值的变化会使刚度矩阵发生变化，进而影响刚性接触网的模态信息。利用试验模态分析得到的模态信息可对刚性接触网的悬挂结构刚度参数进行识别，这构成上述结构动力学正问题的反问题。本文将研究仅用试验模态分析得到的固有频率信息识别刚性接触网的各悬挂结构等效刚度的方法。由于固有频率相比振型向量容易测得。如果该方法被证明可行，将大大减少实验测点和工作量。

1.2 基于遗传算法的优化识别方法

求解本文结构动力学反问题就是通过式(4)以ωi求解各悬挂结构等效刚度，它包含在刚度矩阵[K]中，它也影响振型向量{Φi}，所以方程组(4)是隐式、高度非线性的。为此采用优化算法进行求解，将反问题求解转化为正问题的迭代优化求解，该方法简单有效且可避免直接求解反问题常出现的求逆非适定性问题[16]。该优化问题的目标函数如式(5)所示：

式中：ωexpi为试验模态分析测得的刚性网固有频率值，ωindi为识别出的刚性网固有频率值，它由解式(1)～(4)的正问题求出；n为模态频率总个数。将仿真模型中的待求的各悬挂结构刚度值作为优化变量，最终得到Objv的极小值，若该极小值趋于零，则最终的优化变量即为识别出的各悬挂结构等效刚度。

采用遗传算法求解上述优化问题，通过选择、交叉、变异等操作优化仿真模型悬挂结构刚度值，计算的代数达到最大代数，获得仿真模型最优刚度值。刚性接触网悬挂结构刚度值识别方法流程如图2所示。

图2 刚性接触网悬挂结构刚度识别方法流程图Fig.2 Flow chart of rigidity identification method for suspension structure of overhead conductor rail

具体计算步骤如下。

Step 1：在刚性接触网实物上进行模态试验，获得刚性接触网固有频率ωexpi；

Step 2：随机创建悬挂等效刚度向量初始种群Kindj,j= 1…N，N为悬挂结构总数；

Step 3：将初始种群(随机生成)的刚度向量Kindj输入ANSYS 软件，对刚性接触网在有限元软件中进行有限元模态分析(正问题求解)，获得种群中每一个候选模型个体的固有频率值ωindi；

Step 4：检测和评估step 2 中所产生的候选模型的质量，即根据式(5)计算目标函数；

Step 5：候选模型刚度值的选择、重组与变异，产生新个体，重复Step 3 和Step 4 计算，直到繁殖到最大代数MAXGEN，输出Kindj为悬挂等效刚度向量的最终识别值。

2 刚性接触网模型

刚性接触网由悬挂结构、汇流排、内部接头等部分组成。两端汇流排之间用内部接头连接。汇流排的结构简单，将其力学模型简化为欧拉梁模型，悬挂结构简化为弹簧支撑模型，内部接头的长度与汇流排的长度相比可忽略不计，简化成结点。根据力学模型建立有限元模型，刚性接触网的π 型汇流排与接触线一起等效为beam188 单元，悬挂结构采用弹簧单元等效模拟，弹簧的上端的节点为完全约束节点，下端节点为梁单元节点。内部接头采用质量块单元。各单元类型及其参数详见表1，实物模型、力学模型、有限元模型见图3。

表1 单元类型及参数Table 1 Element type and parameters

图3 刚性接触网模型Fig.3 Model of overhead conductor rail

3 可行性仿真研究

为了从理论上验证本识别方法的可行性，本文采用数值仿真实验进行悬挂等效刚度识别，将试验模态分析用有限元模态分析代替。首先预先给定刚性网的结构特性包括悬挂等效(弹簧)刚度向量Kexpj作为已知的实验结构参数；然后由ANSYS进行正问题分析，计算结构的固有频率作为“试验测量值”ωexpi，这也是正问题的解。然后应用本文刚度识别方法将ωexpi作为已知输入量进行反问题分析，识别悬挂等效刚度Kbestj，若它与Kexpj一致，则证明正反问题的输入和输出一致，亦及从理论上证明本刚度识别方法的可行性。

本节对刚性接触网悬挂结构刚度值识别方法从工况选取、具体收敛过程、刚度识别效果、损伤识别探究方面进行了研究。本节选取了11 种工况对刚性接触网悬挂结构的刚度进行识别。

3.1 工况选取

悬挂结构刚度值识别的搜索范围、跨数、弹簧间等因素都会影响本方法的准确性，因此根据上述不同因素参数的组合选取了11 个工况考察本算法刚度识别的可行性。各种模拟工况参数如表2所示。

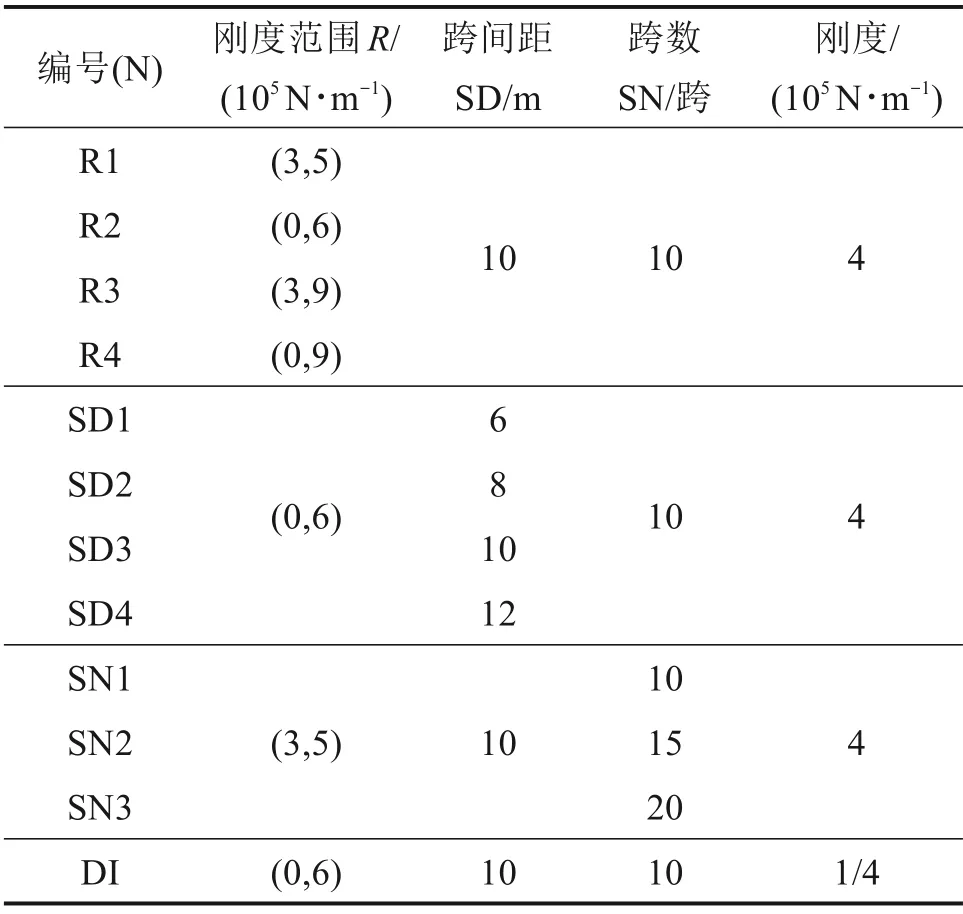
表2 工况参数Table 2 Case parameters

3.2 收敛过程分析

为探究固有频率对弹簧刚度值改变的敏感程度和目标函数收敛状况，选取了工况SD3，研究了其固有频率随着代数的增加而发生的变化(如表3)，各频率的相对误差计算方法如式(6)所示。在前50阶固有频率中，悬挂弹簧的刚度值变化对某些特定阶数的频率影响较大。

表3 SD3情况下频率变化Table 3 Frequency variation in SD3

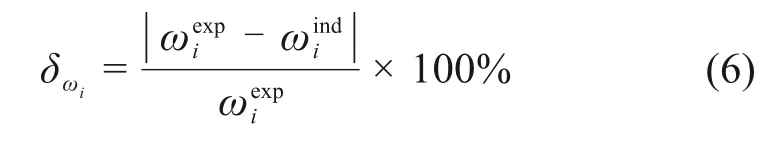
图4 为工况SD2 悬挂弹簧刚度值的收敛情况。在前100 代刚度值的波动较为剧烈，100 代到200代趋于稳定，200 代以后基本收敛到4 × 105N/m 附近，这正是实验模型的悬挂弹簧刚度设定值。由此可见，该方法能够使悬挂弹簧刚度值逐渐收敛到正问题预先给定的悬挂弹簧刚度。

图4 SD2工况悬挂弹簧刚度收敛图Fig.4 Convergence diagram of suspension spring stiffness in case SD2

3.3 刚度值识别效果分析

图5为弹簧刚度识别平均相对误差的变化。平均相对误差δK计算方法如式(7)所示，Kexpi为正问题给定的第i根弹簧的刚度，Kindj为每一代候选仿真模型识别的弹簧刚度值，N为弹簧的个数，亦即优化变量个数。图6 为目标函数Objv 随代数的变化(图例所代表的工况具体含义见表2)。图5 表征刚度识别效果，图6表示识别得到的固有频率与给定值的一致程度。

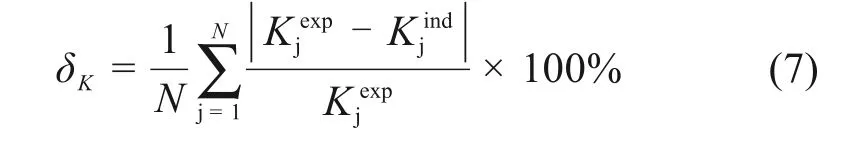
图5(a)和图6(a)选取了不同刚度搜索范围的工况。悬挂结构刚度值得平均误差最终都收敛到10%以内，识别效果最好的R1 工况最终收敛到误差为2.3%。频率的平均相对误差接近0。图5(b)和图6(b)选取了不同悬挂结构弹簧间距，刚度搜索范围为(0，6×105N/m)、总跨数为10跨的工况。悬挂结构结构的间距为10 m 的情况下的弹簧刚度值平均相对误差和目标函数的收敛效果都为最优；间距为6 m 最差；间距为8 m 时弹簧刚度的平均相对误差可减小到4.3%。图5(c)和图6(c)的工况选取了不同跨数10跨，15跨，20跨，刚度搜索范围为(3×105N/m，5×105N/m)，弹簧间距为10 m。图5(c)呈现出跨数越多，优化后的刚度值平均相对误差越差，这是因为随着刚性接触网的跨数越多，总长度越大，弹簧间距不变的情况下，弹簧数量越多，在一次优化识别过程中，同时优化的参数越多，搜索难度越大。在总长度为200 m 时，平均相对误差可以减小到4.2%。

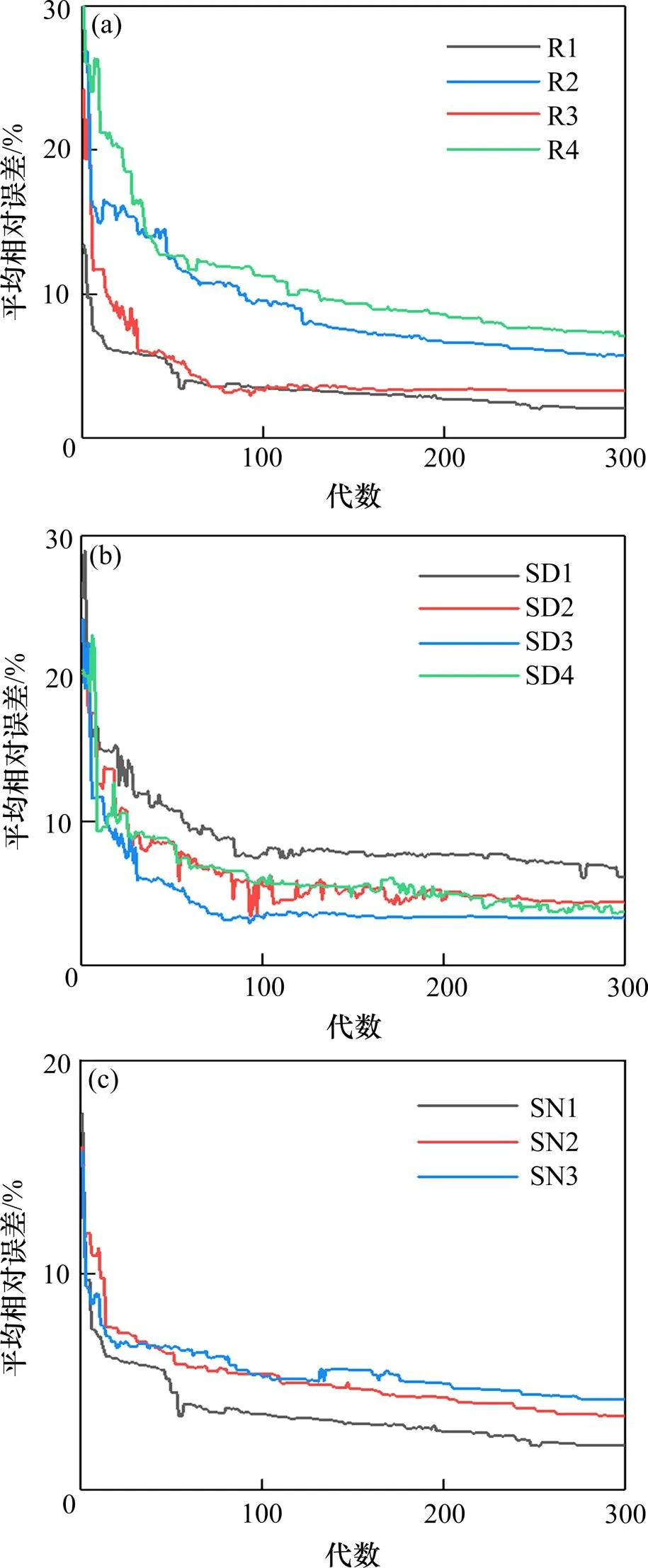
图5 弹簧刚度值的平均相对误差Fig.5 Average relative errors of spring stiffness value

图6 频率(目标函数Objv)相对误差Fig.6 Relative errors of frequency(objective function)

以上仿真结果表明对悬挂弹簧刚度的识别精度大多工况下能控制在5%以内，从而从理论上验证了本文刚度识别方法的可行性。对新建实际刚性网结构进行模态实验后，可应用本文方法识别出实际悬挂刚度，并与设计刚度进行比较，从而检验设计时建立的刚性网仿真模型，并可进行模型修正(用实际刚度代替设计刚度)。传统的弓网模型验证是将仿真模型计算出的弓网接触力与实测弓网接触力进行比较，如果其方差超出标准允许的范围，则认为仿真模型被验证不合格，需要进行模型修正，但验证过程本身并不能指明如何修正。因此传统的弓网模型验证方法是基于结构的动力学响应比较，间接地、笼统地考察受电弓和接触网仿真模型；而本方法是基于模态特性识别刚性网悬挂结构等效刚度，直接地检验刚性网仿真模型的刚度特性，并且刚度识别的优化过程可自动实现仿真模型的修正，这显示出本文方法的优越性。

3.4 损伤识别探究

本刚度识别方法除了上述模型验证和修正功能以外，还可识别损伤弹簧的位置。为探究损伤识别效果，选取了DI 工况，弹簧间距为10 m、跨数为10 跨、刚度搜索范围为(0,6 × 105N/m)。用刚度值减小的方式模拟悬挂结构损伤程度。

图7为悬挂结构弹簧损伤的情况下，刚性接触网的弹簧刚度及其相对误差随代数的变化。正问题中第6 根弹簧的刚度值设置为1×105N/m，其它刚度值设置为4×105N/m。由图可见，第6 根损伤弹簧刚度在第30 代左右已经基本被识别，刚度值迅速下降到1×105N/m，其他弹簧刚度基本在4×105N/m 附近。所以，本算法不但能对损伤弹簧位置进行识别，还能识别到损伤弹簧的实际刚度值，损伤弹簧刚度值的识别误差可小于到0.05%。本刚度识别方法可用于实际服役中的刚性网结构的悬挂结构刚度识别，并与4.3 小节中识别出的新结构或维修后结构的刚度比较，可确定损伤位置和损伤程度，从而确定维修方案。因此本方法可用于实验室刚性网的损伤识别研究和实际线路刚性网检测，提升运维技术水平。