整体浇筑梁预应力束自动布置的分步算法

张德旺，秦寰宇，宋旭明

(1. 中铁第四勘察设计院集团有限公司，湖北武汉 430063；2. 中南大学土木工程学院，湖南长沙 410075)

PC 梁桥中预应力束的布置直接影响桥梁的承载能力和使用性能。目前，预应力束的布置主要依靠设计者反复调索来实现，较为耗费时间和精力，由于设计者经验和水平的差异，同样桥梁的预应力钢束布置可能差异很大。因此，探索预应力束布置的优化算法，依此编制预应力束自动布置的软件是一项亟需展开的工作。对于预应力钢束的优化设计，国内外学者开展了许多研究[1-2]。UTRILLA 等[3]基于线性规划的最快速下降方法得到了结构几何学上的最佳布索位置和最小索力。楼卓[4]运用多元罚函数法和多元包维尔法对某T 形简支梁进行了优化设计。何雄君等[5]按a-水平解集解法对预应力进行模糊优化决策。赵新[6]利用复形法对变截面连续箱梁进行优化，证明预应力束比混凝土优化的潜力更大。HEMANDEZ 等[7]以预应力钢束最少为目标函数，采用单纯形法对某工字型梁进行优化设计。刘桂林[8]建立了不同设计变量的优化模型，并以此开发连续箱梁桥优化系统。AYDLN等[9-13]以梁体总造价最低为目标函数，运用了遗传算法、梯度搜索法等方法求解设计变量。MARTÍ 等[14]引入能量作为目标函数对PC 梁进行优化设计。以上预应力的优化算法多为局部优化，无法实现预应力束在程序中的全自动布置，或者将预应力束线形和数量同步计算，忽略预应力束线形的构造要求，得到的线形无法应用于工程。本文针对整体浇筑施工的简支或连续梁，提出预应力束全自动设计的分步算法。将预应力束线形和数量分步计算，在优化全梁弯曲能量的基础上，根据规范要求控制主梁应力并考虑预应力束的构造要求，弥补了传统优化算法的不足。基于Matlab平台已经开发的“跨座式单轨设计程序”，在其中嵌入“预应力设计”模块对柳州跨座式单轨桥梁进行自动布束研究，结果表明桥梁的各项指标控制良好，布束方案可行。

1 预应力钢束布置的分步算法

分步算法的主要步骤：首先根据主梁弯矩包络图形状确定预应力束的线形；然后利用弯曲能量最小的决策系数法计算各类型束的数量，最后根据各截面应力状态进行预应力束的局部调整。

1.1 预应力束线形计算

整体现浇梁预应力束线形设计基于结构设计荷载组合下的弯矩包络图，钢束线形基本与弯矩包络图形状一致，图1为某四跨连续梁的弯矩包络示意图。

图1 四跨连续梁的弯矩包络示意图Fig.1 Bending moment envelope diagram of a four-span continuous beam

将预应力束布置在构件的最佳界限区内[15]，正弯矩区段预应力束布置在主梁下部受拉区，负弯矩区段预应力束布置在上部受拉区。图1的弯矩包络图中ab，ac段为边跨正弯矩钢束的最小、最大布索范围；be，cd段为支座2负弯矩索最大、最小布索范围…，依此类推，可基本确定全桥预应力束的布置范围。

纵向预应力束通常分为腹板束、顶板束和底板束。预应力束线形的计算首先需要识别各种类型束，其次每种类型束由导线点坐标、曲线半径描述，其中曲线半径依规范取值。

1.1.1 区分预应力类型束

由于腹板束可以较好地适应弯矩图变化，效率高，通常布置多排。图2 是某梁段第2 支座处腹板束的布置图，图中有3种腹板类型束。

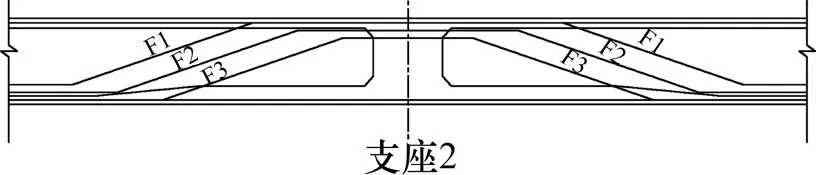
图2 腹板束局部布置图Fig.2 Local layout drawing of web prestressed steel strands

根据图1，腹板钢束与梁中性轴相交的节点分布在bc，de之中，设布置n排腹板束，bc,de,fg…区间长分别为l1,l2,…,l2m(m为中支座数)，每个区间n排腹板束的间距分别为d1,d2,…,d2m，则n排腹板束布置的约束公式为：

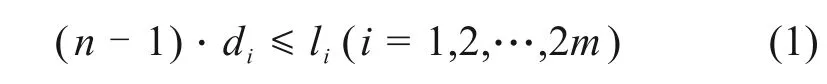
根据弯矩包络图计算li，令di取预设常量d，由此得到腹板类型束数量n的计算公式：

顶板束和底板束主要为短束，根据弯矩包络图分别布置于支点上缘和跨中下缘，对于全梁应力的调整，可布置少量通长顶、底板束。通长束的布置相对单一，顶、底板短束的类型束计算方法同腹板束。

1.1.2 描述各预应力类型束

对于腹板束，确定类型束种类时，已知各类型束与中性轴交点，通过计算弯起角度，结合对应位置梁高，即可确定所有导线点坐标。图3为中间支座局部弯矩包络图，腹板束弯起部分在梁中性轴上半部的轴向区间为[bc,ac]。

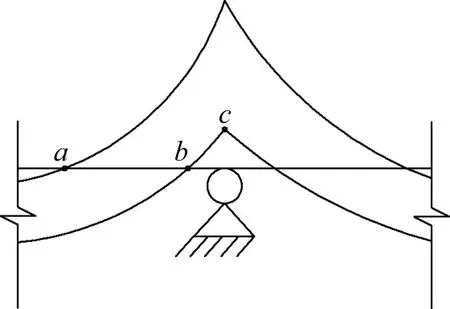
图3 中间支座局部弯矩包络图Fig.3 Local bending moment envelope diagram of the intermediate support

设梁高为h，令钢束中心与梁边缘最小距离为h0，中性轴距梁底高度为h1，预应力束管道在竖直方向的间距为hj，则n排腹板束，第i种类型束在中性轴上半部的弯起高度为：

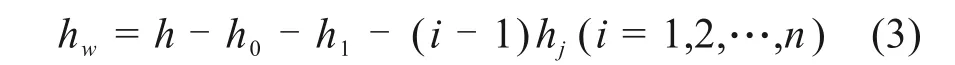
设bc=p，ac=q，已知腹板类型索有n组，彼此间距为d，则腹板束弯起部分在梁中性轴上半部的轴向区间为[p,q- (n- 1)·d]。弯起角度的取值范围见式(4)：

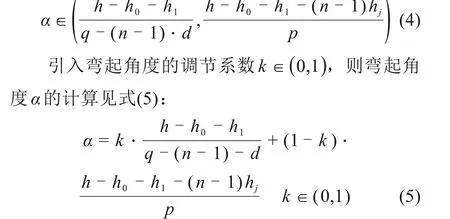
同理，梁端部腹板束弯起，先确定弯起范围，最后在范围内尝试不同取值方案。对于顶、底板束，其线形分别随梁顶、底部线形变化，在张拉及锚固端根据规范及张拉空间要求设置弯起段。确定起止点、张拉端和锚固端即可确定顶底板各导线点坐标。

1.2 预应力束数量计算

钢束布置分为2 类：第1 类钢束跟随弯矩包络图的走势布置，如腹板束和部分顶底板短束；第2类钢束根据全梁应力计算结果进行局部调整，如顶底板通长束。基于贪心算法[16]的思想逐步计算2类钢束数量：首先调整第1类钢束数量使梁体达到当前弯曲能量最小的状态，在此基础上适当调整第2类钢束数量，使主梁上、下缘应力控制在设计规范容许范围。软件实施过程中，分别采用决策系数法和应力控制法计算第1 类和第2 类钢束数量。

1.2.1 决策系数法

取梁中抗弯刚度为EI的微段dx，计算该微段内弯矩M引起的应变能[17]dVε：

式中：针对i单元，MLi，MRi为单元两端弯矩；Ei为弹性模量；Ii为弯曲惯性矩；li为单元长度。

不计预应力作用进行有限元分析，得到结构初始弯矩状态ML0和MR0，基于线性规划[18]的思想，假设通过调整第1 类钢束数量{e}得到最终的目标弯矩分布状态ML，MR，表示为式(8)：

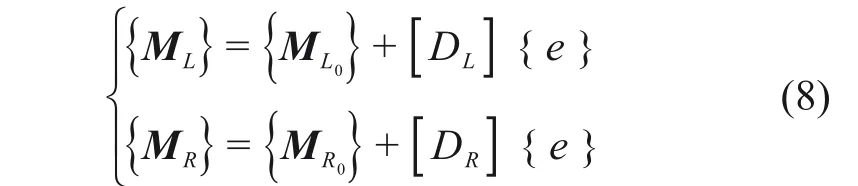
式(8)中{e}为决策变量，[DL]，[DR]为决策系数。决策系数表示对应单位预应力束的数量变化导致的结构弯矩变化。

式(7)中Vε作为决策目标用矩阵运算表示为：

{e}即第1 类钢束数量，依此布置钢束可使梁在当前状态下有最小弯曲能量，对应较为合理的弯矩分布状态。

融资难是制约科技型创业企业发展的主要因素。根据对54家样本科技型创业企业的调查结果，其中有融资需求的达47家，占比87.04%，其中有5家已经或正在进行众筹融资，其余的企业虽然有融资需求，但因为对众筹融资渠道和流程缺乏了解，难以及时获得创业所需资金。部分企业表示虽然听说了国家鼓励众筹融资的相关政策，但是不知道如何设计众筹融资方案和选择合适的众筹平台，导致无法有效发挥众筹对科技创业的支持作用。

1.2.2 应力控制法

全预应力混凝土梁在预加力和使用荷载作用下，截面正应力按照规范取约束条件。若设计不仅要求结构截面上、下缘不出现拉应力，还要求σp应力富余，则约束条件可表示为：

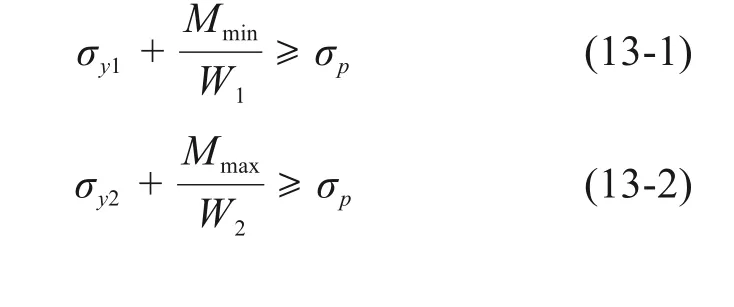
式中：σy1，σy2为预加力在截面上下缘产生的应力；W1，W2为截面上下缘的抗弯模量；Mmax，Mmin为设计荷载组合下的截面内力。

若布置第2类钢束在梁上、下缘产生的预加力分别为N1，N2，计算应力为：

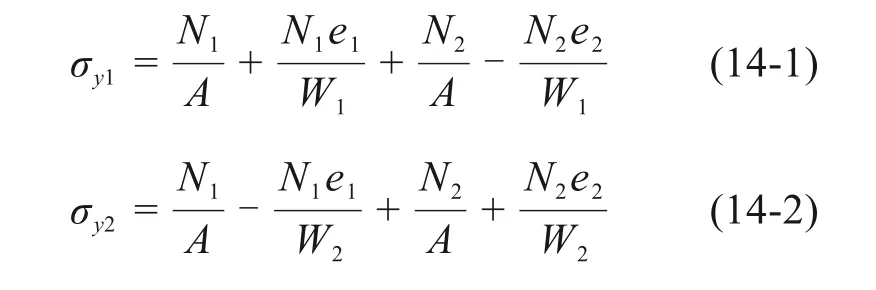
设每束钢束面积为sy，永存预应力为σy。联立式(13)～(14)，计算可得截面上、下缘布置第2 类钢束数目n1，n2为：

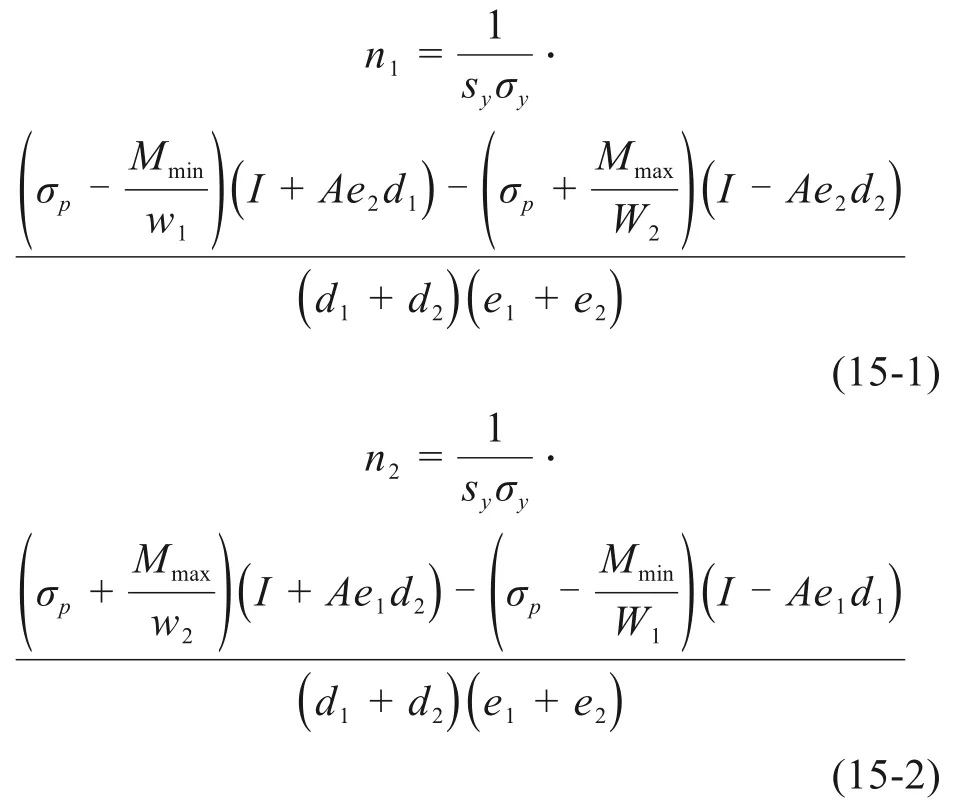
式中：e1，e2为上下缘钢束重心距截面重心的距离；I为弯曲惯性矩；A为混凝土截面面积，d1，d2为截面上下缘距截面重心的距离。

2 预应力束自动布置的软件实现

基于预应力束自动布置的分步算法，在“跨座式单轨设计程序”中开发“预应力设计”模块，程序计算流程和GUI 界面分别如图4 和图5 所示，计算步骤如下：

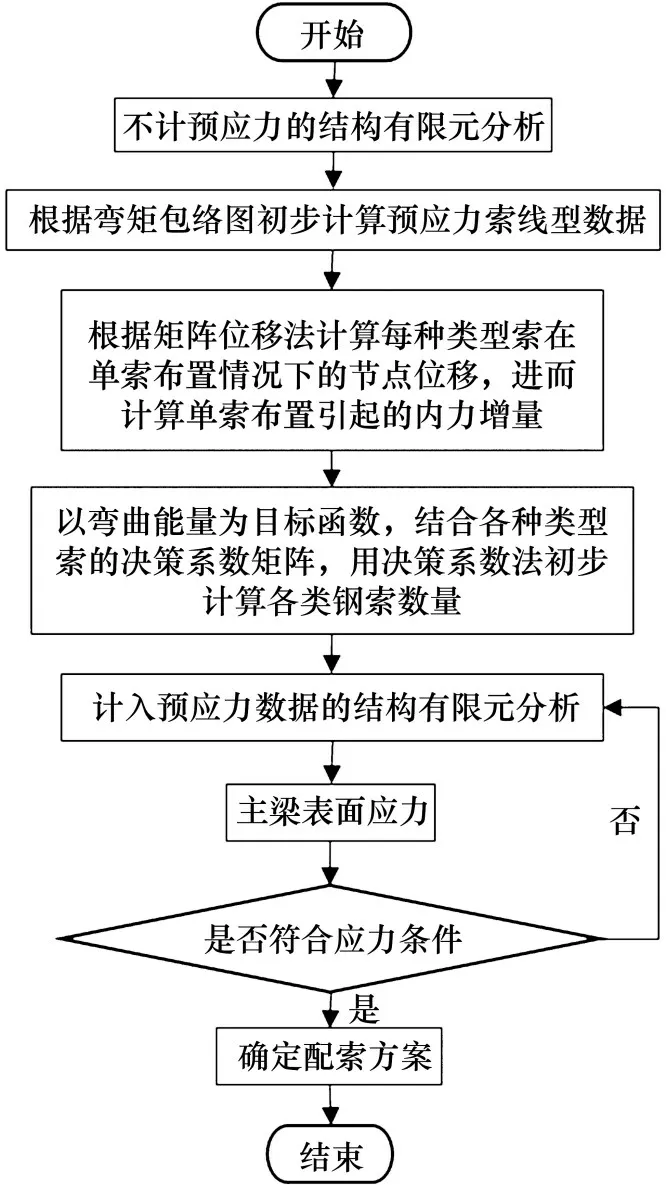
图4 程序计算流程图Fig.4 Flow chart of program calculation

图5 “跨座式单轨设计程序”图形用户界面Fig.5 Graphical user interface of“Straddle Monorail Design Program”

2) 依据初始弯矩包络图及桥梁的构造尺寸计算预应力束的各种线形方案；

3) 依据预应力束面积、张拉控制力等初始设计条件，计算每种类型束作用下结构弯矩内力增量，形成决策系数矩阵。其中，运用矩阵位移法进行有限元分析时，包含预应力束刚度矩阵、预应力损失和等效节点荷载矩阵的计算；

4)依据决策系数法初步计算第1类钢束数量；

5) 将初步确定的钢束线形、数量等数据代入模型，重新进行有限元分析；

6) 提取主梁上、下缘应力，运用应力控制法计算第2类钢束数量；

7)重复步骤5 和6，直至主梁应力结果符合控制条件；

8)确定最优配束方案。

在软件的使用过程中，可直接获得推荐的配束方案，也可以通过2种人机交互的方式得到不同的配束方案：第1种是调整初始参数，例如式(5)中的调节系数k，曲线半径和应力控制条件等；第2种是修改计算的线形，包括第1类钢束的类型束种类和导线点坐标。

3 跨座式单轨连续梁自动布束算例

3.1 工程背景及计算模型

柳州跨座式单轨采用多固定连续梁体系，一侧边墩采用纵向活动支座，其余支座均采用固定铰支座，纵向水平力由多个墩柱共同承担。轨道梁采用C60混凝土，截面为矩形，梁宽0.69 m，跨中梁高1.8 m，支点梁高2.2 m，采用圆曲线过渡，曲线半径51.4 m。设计活载为CMR2 型车辆荷载，远期8 辆编组。以3×30 m 梁为例，实际施工方法是将预制梁简支后再变连续，为探究分步算法的实用性，此连续梁拟采用整体现浇法完成。分别用Midas Civil 和“跨座式单轨设计程序”建立计算模型，每跨梁分为22个单元，几何模型见图6。

图6 柳州单轨三跨梁有限元模型Fig.6 Finite element model of a three-span part of Liuzhou monorail

3.2 计算结果

根据图4 的计算流程，步骤1 计算的初始弯矩包络图如图7，步骤2 计算各类型束线形，考虑单轨梁的箱体内部狭小，无法张拉预应力短束，除去程序自动计算的顶板短束和中跨底板短束，得到线形如图8。预应力束线形有多种备选方案，限于篇幅，图8 为式(5)中k= 0.5 的计算方案。腹板束为F1～F3，边跨底板短束为B1和B2，顶、底板通长束为T0和B0。

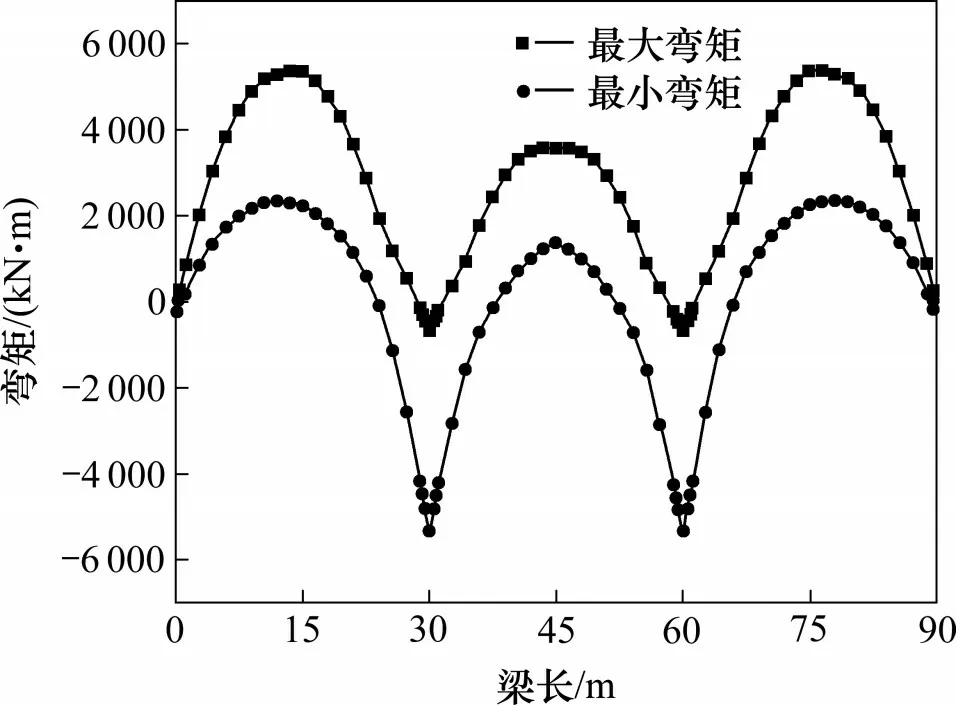
图7 设计荷载组合的弯矩包络图Fig.7 Bending moment envelope diagram under the design load combination

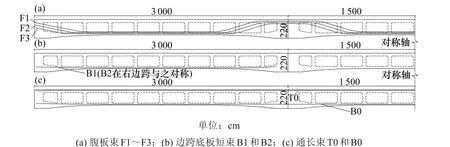
图8 各类型束线形Fig.8 Geometry of various prestressed steel strands

设计钢束类型为5-7φ5，张拉控制应力取1 270 MPa。步骤3 计算各种类型束的决策系数在主梁各单元节点的分布如图9。

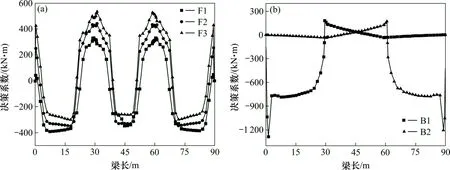
图9 各类型索的决策系数Fig.9 Decision coefficient of various prestressed steel strands

步骤4 依据式(12)计算F1～F3 和B1 和B2 的数量，布置完以上钢束后，由步骤5 计算主梁正应力，步骤6 取应力约束区间为(0,22)MPa，依据式(15)计算T0 和B0 的数量，最终确定的各类预应力束数量如表1所示。

表1 各类型索数量Table 1 Number of various prestressed steel strands

“跨座式单轨设计程序”依据该配束方案，计算主梁上、下缘应力极值分布如图10。

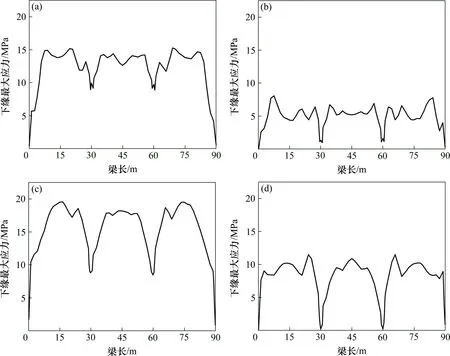
图10 主梁上、下缘应力Fig.10 Stress on the upper and lower edges of the beam

在Midas Civil 模型中输入计算的配束方案，由于Midas 和“跨座式单轨设计程序”在本构模型、预应力损失计算等方面存在偏差，两者的应力结果也存在偏差。在主梁的关键截面处，两者计算的正应力结果，以及本程序相对Midas的应力结果的最大偏差见表2。

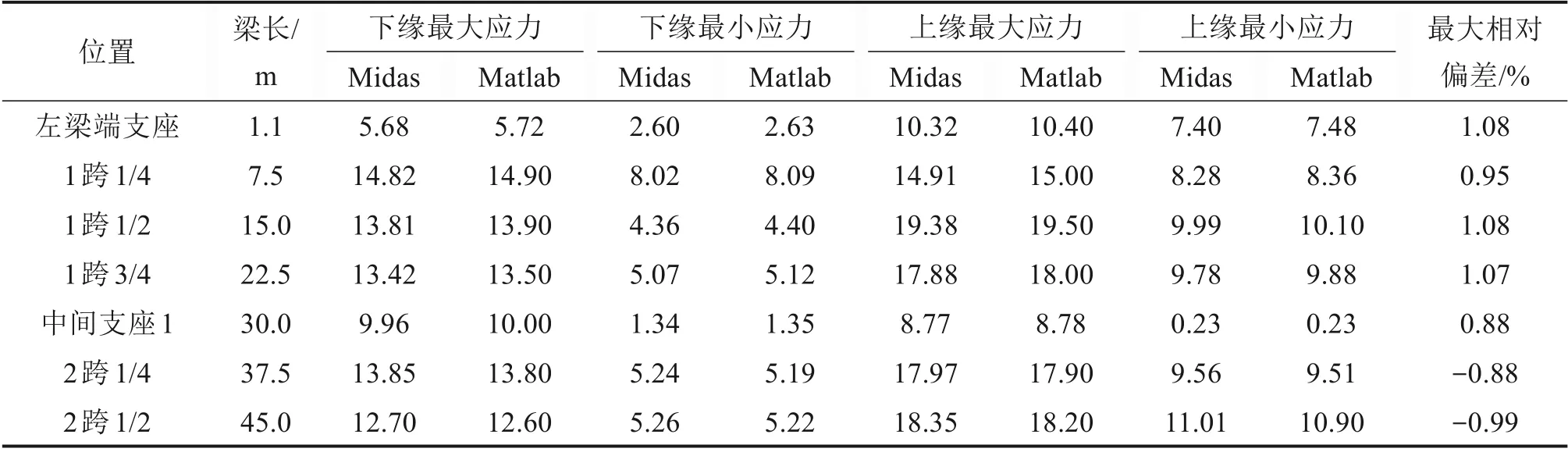
表2 Midas和“跨座式单轨设计程序”计算应力对比Table 2 Comparison of calculated stress between midas and straddle monorail design programMPa

从表2 可知，Midas Civil 和“跨座式单轨设计程序”计算应力最大偏差为1.08%，表明“跨座式单轨设计程序”的有限元计算模块有良好的准确性。计算的配束方案中各类预应力束的数量合理，正截面应力指标符合规范要求，证明预应力束自动布置的分步算法可应用于工程实践。

4 结论

1) 分步算法中计算的预应力束线形组合是多元化的，可以给设计者提供方案比选。

2) 在“跨座式单轨设计程序”基础上开发“预应力设计”模块，使预应力计算考虑了预加力的损失和钢索刚度对单元的影响，让预应力设计由粗略估束转变为相对精确的计算。

3) 分步算法弥补了传统优化算法的缺陷：传统的整体优化算法，将预应力束线形和数量同步优化，忽略钢束线形的构造要求；传统的局部优化算法，无法对预应力进行全体系设计，因此无法实现程序化全自动布束。

4) 预应力索自动布置的分步算法目前不考虑其他复杂施工过程，可在整体浇筑桥梁的设计中推广使用。