成层软土地基中轴横向组合受荷桩内力与位移分析
2021-12-22雷皓程赵炼恒张鹏鹏龙秋亮
雷皓程,赵炼恒,2,张鹏鹏,龙秋亮
(1. 中南大学土木工程学院,湖南长沙 410075;2. 湖南铁院土木工程检测有限公司,湖南长沙 410075;3. 湖南路桥建设集团有限责任公司,湖南长沙 410007)
成层软土地基中,其物理力学性质沿深度的较大差异性难以用简单均一的荷载传递模型进行描述,导致计算桩基础的竖向与横向力学响应均为复杂的非线性问题,而同时分析桩基础的竖向与横向力学响应及其耦合效应更为复杂。因此,有必要对成层软土地基中轴、横向荷载联合作用下桩的力学响应及其承载变形的耦合效应进行深入探讨。LU 等[1]研究了砂土中的单桩在组合荷载下的影响机理和规律,研究表明竖向荷载将使桩侧土产生致密效应同时使桩身产生附加弯矩,最终的影响效果是上述2 种效应的叠加;KARASEV等[2]通过现场试验观察到水平荷载将使单桩产生附加沉降,其原因可归结为水平荷载的存在减小了桩侧摩阻力[3];三维有限元分析表明[4-5],竖向荷载对砂土中桩基横向承载力有一定程度的增大作用,但降低了黏土中桩基的横向承载力。以上研究表明,组合荷载下单桩的耦合效应极其复杂,轴、横向荷载对竖向承载力与横向承载力相互影响。HAZZAR 等[6]利用FLAC3D 对竖向荷载下单桩的横向响应进行了三维建模分析,具体分析了垂直荷载对桩侧承载力和抗弯承载力的影响;赵明华等[7-10]基于m法假定,假设轴力和侧阻线性分布,采用解析法、幂级数法、有限杆单元法、有限差分法对轴横向受荷桩的P-Δ 效应进行了定量分析;张磊等[11]等基于地基反力法获得了单桩轴横向荷载下内力的半解析解;竺明星等[12]则通过矩阵位移法求解了轴横向受荷单桩的内力位移。但现有理论分析方法中,未能将单桩的竖向力学响应分析和横向力学响应分析统一起来,忽略了单桩竖向力学响应计算精度对单桩横向力学响应的影响,虽也能较准确计算出单桩P-Δ效应的大小,但难以同时准确计算出桩顶各向位移,从而不能准确计算单桩在轴横向同时受荷时的各向刚度,导致无法直接推广至群桩计算。尤其在成层软土地基中,因其荷载传递的非线性,使上述问题更明显。本文根据成层软土地基的力学性质,采用能较真实反映软土地基桩-土界面的荷载传递模型,将荷载传递法和p-y曲线法结合,建立轴横向荷载同时作用下的单桩分析模型以及挠曲线微分方程,以基于荷载传递法计算所得的桩身轴力和桩侧摩阻力,利用有限差分求解挠曲线微分方程以计算桩身内力位移,最终获得单桩在轴横向联合荷载作用下的桩顶竖向位移与水平位移以及耦合效应大小。
1 桩-土界面接触模型
1.1 桩侧阻力模型
本文采用一种考虑初始极限剪应力的分段双曲线模型描述桩-土荷载传递性状[13]:
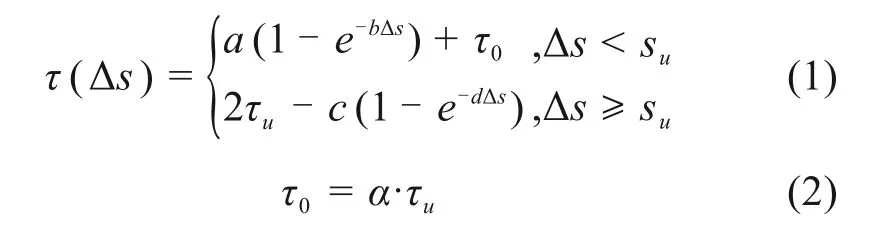
式中:τ(Δs)为某一深度处的桩侧摩阻力;α是初始临界侧摩阻力与极限侧摩阻力之比;τu是极限侧摩阻力;τ0是初始临界侧摩阻力;a,b,c,d是4个经验系数,其值由文献[13]中的方法确定。
1.2 桩端阻力模型
采用一种直线+双曲线的分段函数模型模拟软土地基中单桩桩端荷载传递特性[14]:

式中:fb(s)是桩端沉降为s时的桩端阻值;sb,k,j,l为4 个经验参数,其值由文献[14]中的方法确定。
1.3 横向土抗力模型
本文采用一种经验p-y曲线模拟单桩受横向荷载时桩周土横向力与横向位移间的非线性关系[14]:
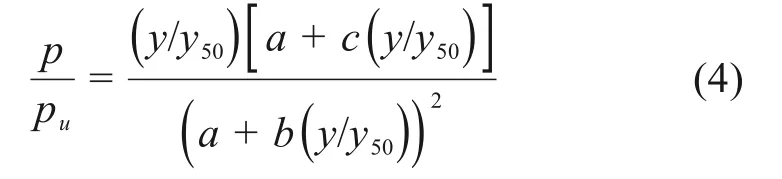
式中:P为某深度处土的水平土抗力;y为某深度处土的水平位移;Pu为某深度处土的极限水平土抗力,y50为土反力是极限水平土抗力一半时的水平位移,a,b和c为待定参数。以上所有参数求解均由文献[14]中的方法确定。
2 单桩分析模型和微分方程建立
2.1 单桩分析模型
以单桩地面处截面中心为原点,水平方向为y轴,竖直方向为x轴建立直角坐标系。单桩埋深为L,截面面积A,弹性模量E,截面惯性矩I均为定值,桩侧土的弹性模量为Es。将地面以下桩身等分为n段,每分段长度为h。桩身轴力、桩侧摩阻力、水平土反力、剪力、弯矩的正方向如图1所示。其中-1,-2,n+1和n+2为虚拟点。

图1 单桩受力分析模型Fig.1 Stress analysis model of single pile
在桩顶竖向荷载P,水平力Q和弯矩M作用下取桩身任一单元,可知单元体受竖向的轴力、侧摩阻力以及横向的剪力、弯矩、桩侧土水平反力。
2.2 微分方程建立
由力矩平衡有:


式(10)即为轴横向受荷桩的挠曲线微分方程,式(10)中含有EI,N,f3 个常量,其中抗弯刚度EI已知,因此,需求解x和y,必须先求解桩身轴力N和侧摩阻力f。
2.3 利用荷载传递法[15]求解轴力N和侧摩阻力f
步骤1:计算桩端荷载Nbn
假设桩端沉降sbn,由式(3)计算桩端荷载Nbn。步骤2:计算桩段n的等效位移Smn

步骤8:向上递推求解
重复步骤2~步骤7,即可获得桩顶荷载P,桩顶位移S,桩身各节点处的轴力N和侧摩阻力f。
3 微分方程求解
1) 差分方程的建立
利用中心差分理论将式(10),式(7)~式(9)展开,可得到式(17)~式(19):

2)边界条件
假设桩端剪力Qn,桩端弯矩Mn为0,已知桩顶剪力Q0,桩顶弯矩M0,则由式19(b)和19(c)可得:

3) 求解y值
步骤1:求解yn+2和yn+1联立式20(c)和20(d)可得:


4) 迭代求解
步骤1:求解第1组A,B,C的值
假设A0~An的值,由式(29)求解B0~Bn,C0~Cn的值;由式(31)、式(33)求解A-1,B-1与A-2,C-2。至此,第1组A,B,C的值已求出。
步骤2:求解y-1和y-2
将相关A,B,C的值代入式(31)和式(33)中,可求得y-1和y-2的值。
步骤3:求解y0~yn+2
将各节点A,B值依次代入式(29)中,求解各节点y值。至此,第1组所有所有y值已得出;
步骤4:求解pi与Esi
将各节点的y值代入式(4)求得各节点的p值,进而由Es=p/y求得各节点Es值。
步骤5:求解新的一组A,B,C的值
将各节点Es值代入式(18)求得新的一组A值,由式(29)求解B0~Bn,C0~Cn的值;进而由式(31),式(33)求解A-1,B-1与A-2,C-2。至此,新的一组与计算有关的A,B,C的值已求出。
步骤6:重复步骤2~步骤5,直至满足精度。
4 算例分析
选取2 根试桩作为本文研究对象,其中M1 试桩[9]为某桥梁桩基,其地基土物理力学性质参数及计算参数见表1;M2 试桩[16]位于某软土地区,地基土物理力学性质参数及计算参数取值见表2。

表1 M1试桩桩身参数与地基土物理力学性质参数Table 1 M1 test pile body parameters and foundation soil physical and mechanical properties parameters
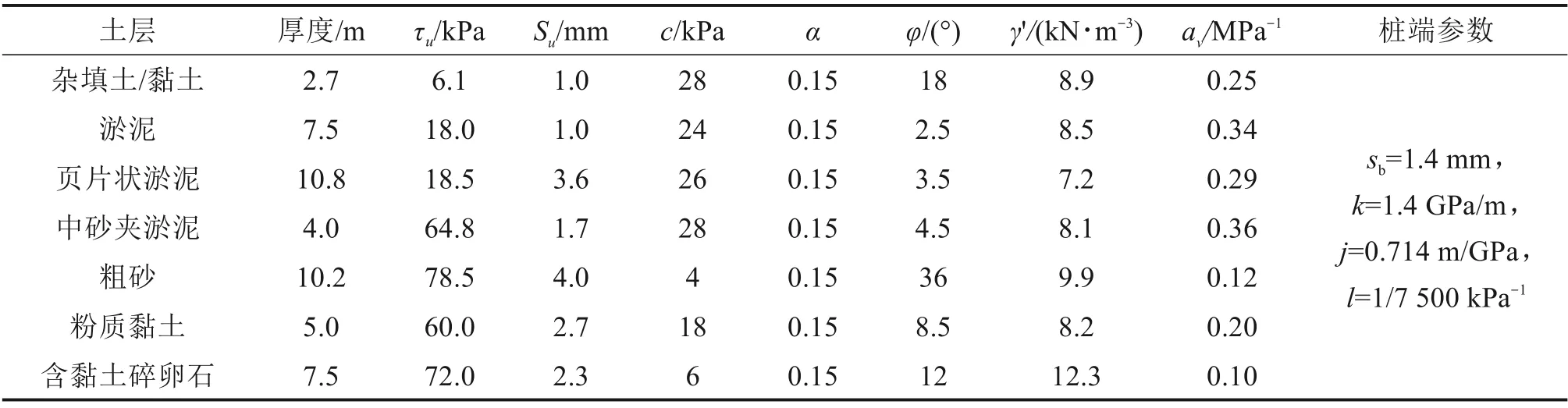
表2 M2试桩桩身参数与各层土物理力学参数Table 2 M2 test pile body parameters and physical and mechanical parameters of each layer of soil
4.1 P-Δ效应计算方法验证
利用本文结合荷载传递法与p-y法的轴横向受荷桩内力位移计算方法对M1 试桩进行分析。本文计算结果与文献[9]结果如表3 所示,其中方法1,方法2 和方法3 所示数据为文献[9]所记录。由表3可知,由本文计算方法所计算得的桩顶位移以及附加桩顶位移与文献[9]计算值大致相同,表明本文方法应用于轴横向受荷桩的内力位移分析是合理可行的。

表3 桩身位移计算结果Table 3 Calculation results of pile displacement
4.2 轴横向受荷桩桩顶各向位移计算
利用本文方法与采用经验侧阻分布的方法对M2试桩各向位移进行计算,结果如图2所示。

图2 桩顶各向位移Fig.2 Displacement of pile top in all directions
由图2 可知,由本文结合荷载传递法与p-y曲线法计算所得的桩顶水平位移与根据经验桩身侧阻分布计算所得的桩顶水平位移存在差异,其中水平位移最大差值可达20%,此差异即由侧阻分布大小与分布形式的不同使竖向荷载计算不够准确导致的。因此如竖向荷载计算不准确,也将导致水平位移计算不准确。而对于成层软土地基,因其土层分布较为复杂、荷载传递性质多为非线性,经验的常数侧阻分布形式难以准确描述其荷载传递机理而不能准确计算桩身竖向力学响应,从而导致桩身各向位移计算均不准确,进而影响群桩各向刚度计算。而本文轴横向受荷桩内力位移分析方法则能考虑竖向力学响应的计算精度。
4.3P-Δ效应大小及影响因素分析
以M2 试桩为例,对轴横向受荷桩P-Δ 效应大小及影响因素进行分析,计算结果如图3~5所示。

图3 桩身水平位移对比Fig.3 Comparison of pile horizontal displacement
由图3~5 可知,当桩顶竖向荷载为12 000 kN时,桩身位移、弯矩、剪力都较桩顶竖向荷载为0时有显著变化,表明在轴横向荷载联合作用下,桩身将产生附加内力与位移,即存在P-Δ效应。轴横向荷载联合作用下,桩身地面处水平位移、桩身最大弯矩分别增大约24%和4%,桩身最大剪力无显著变化,但最大剪力产生的深度略有下移。但不论竖向荷载是否存在,桩身水平位移、弯矩、剪力几乎都在同一深度处(埋深21 m 处)趋近于0。以上差异表明,单桩在轴横向荷载联合作用下将产生附加位移与内力,即竖向荷载的存在会增大单桩的横向力学响应。如不考虑P-Δ效应,计算结果将与实际结果产生较大偏差,尤其是桩身位移,但竖向荷载几乎不会影响桩身内力位移沿深度的分布情况。

图4 桩身弯矩对比Fig.4 Comparison of pile bending moment

图5 桩身剪力对比Fig.5 Comparison of pile shear force
以图3 中桩身内力位移刚好趋近于0 的深度为界,本文定义其以上土层为上部土层,以下为下部土层。由图6可知,对桩身位移产生影响的主要为上部土层,而下部土层对桩身内力位移几乎无影响。上部土层抗剪强度指标越小,桩身水平位移越大,且当上部土层越“软”时,桩身水平位移随竖向荷载的变化非线性程度越大。以上分析表明,对水平荷载作用下桩身内力位移响应影响较大的为上部土层(桩身内力位移零点以上的土层),且上部土层也对桩身P-Δ效应程度存在影响。

图6 土工参数分析(Q=600 kN)Fig.6 Geotechnical parameter analysis(Q=600 kN)
由图7 可知,相同竖向荷载与水平荷载作用下,桩身泥面处水平位移随竖向荷载增加的幅度随桩径的增大而减小,表明增大桩径可显著减小P-Δ 效应。由图8 可知,在桩长分别为47.7,57.7,67.7 m时,桩身泥面处水平位移随竖向荷载增加的曲线几乎重合,桩长对单桩P-Δ 效应影响不明显,表明在多层软土地基中,增加桩长对减小桩身水平位移作用极其有限。
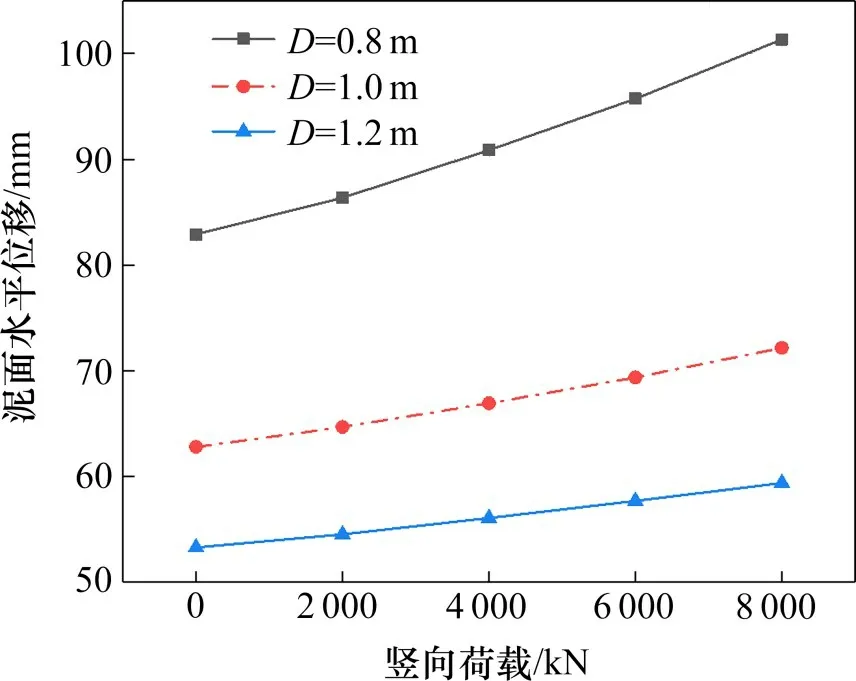
图7 桩径分析(Q=600 kN)Fig.7 Pile diameter analysis(Q=600 kN)
5 结论
1)本文提出的将荷载传递法与p-y曲线法统一结合的方式应用于轴横向受荷桩P-Δ效应分析是合理可行的,能较准确计算出轴横向受荷桩因竖向荷载的存在而产生的桩身附加位移附加内力。
2) 成层软土地基中,若忽略了轴横向受荷桩竖向力学响应的计算精度,将会导致桩身横向力学响应计算出现偏差,从而不能同时准确计算桩身各向位移。
3)对桩身横向力学响应以及P-Δ效应存在影响的主要为上部土层(桩身内力位移零点以上的土层),下部土层(桩身内力位移零点以下的土层)对其几乎无影响,即上部土层越“硬”,桩身横向力学响应与P-Δ效应越小。
4) 增大桩径可显著减小桩身横向力学响应与P-Δ 效应,而增加桩长对减小桩身横向力学响应与P-Δ效应作用极其有限。
