基于BRGWO算法和滤波Smith预估器的气弹系统时滞控制
2023-02-27李迺璐范瑞杰骆紫薇曹智广
李迺璐,范瑞杰,骆紫薇,曹智广
(扬州大学 电气与能源动力工程学院,江苏 扬州 225100)
翼型气弹系统广泛存在于飞行器、风力机和直升机等,在实际气弹控制系统不可避免的存在的时滞环节,如来自驱动器、闭环信号传输的时滞等。一方面,气弹系统工况通常较为复杂,存在风速不确定变化、负载干扰等;另一方面,气弹系统的颤振特性对于系统参数变化较为敏感,严重时会在短时间内极速恶化[1]。由于气弹敏感性和工作环境复杂性, 时滞带来的气弹控制迟延,易导致颤振特性恶化,严重时会造成系统毁坏[2]。因此,需要研究在不确定工况下,可以克服时滞影响的气弹系统控制方法,从而保证气弹系统的安全高效运行。
目前,翼型气弹系统最常应用的控制器为比例-积分-微分(proportional integral derivative,PID)控制器和线性二次型(linear quadratic regulator,LQR)控制器。PID 控制器由于结构简单、可靠性高和应用性强,应用最广泛。文献[3]设计了PID控制器,有效减少了翼型气弹系统的挥舞位移; 文献[4]基于尾缘襟翼结构,利用PID控制器,实现了风力机叶片翼型的气弹控制。 LQR控制器考虑了驱动限制问题,基于气弹系统的状态量设计状态反馈控制器,可以在保证气弹控制效果的同时进一步降低驱动器劳损[5]。近年,多种先进控制器方法应用于翼型气弹系统控制,在多种工况下可以改善动态特性、提高气弹控制的鲁棒性。文献[6]在风况下设计了预测控制振动器,有效减小了翼型挥舞和扭转运动;文献[7]利用鲁棒控制器,在周期时变干扰下保持了良好的气弹控制效果;文献[8]设计了自适应内模控制器,在多种不确定工况下增强了翼型气弹控制的鲁棒性。
上述文献的气弹控制器设计主要基于理想非时滞系统,并未充分考虑实际系统中可能存在的时滞环节及其影响。在不确定工况下,迟延的控制信号难以及时有效地控制气弹系统,易会造成系统失稳。因此,针对时滞和不确定工况,需要提高气弹控制器的有效性和鲁棒性,核心在于解决时滞下的气弹控制问题。
针对系统时滞问题,Smith预估器在各类系统及工程问题中得到了广泛的应用[9-12]但当系统或环境发生变化时,Smith预估器易存在预估模型失配的问题,导致其无法充分发挥时滞补偿的作用,造成时滞控制效果恶化,模型失配较大时甚至出现系统振荡。 为此,国内外学者提出了一系列针对Smith预估器的优化方案。文献[13]针对炼油控制时滞系统,设计了PI改进型Smith预估器控制结构,在系统变参数和干扰工况下明显改善控制的鲁棒性;文献[14]针对工业对象滞后控制问题,将PI和PD作为主副控制器,提出了一种改进型Smith预估器结构,在模型失配严重时保持了较好的控制效果;文献[15]利用一阶滤波器设计Smith预估器,针对一阶时滞稳定系统、一阶时滞不稳定系统和多输入多输出不稳定系统具有良好的控制性能。上述文献研究大多针对具有较长时滞的工业过程,而翼型气弹系统具有不确定小时滞、系统参数敏感、气弹特性变化快和干扰多等特点,目前,针对这类系统的Smith预估器控制研究还较少。
Smith预估器的应用还依赖于选择合适的控制参数。Smith预估控制参数的整定方法主要包括经验法[16-17]、神经网络算法[18-19]和智能优化算法[20-21]等,其中,智能优化算法由于智能化程度高、寻优效果好和整定效率高受到关注。Mirjalili等[22]在2014年提出了一种灰狼优化算法(grey wolf optimization, GWO),该算法根据大自然中灰狼的等级制度,模拟灰狼合作捕猎行为,达到寻优的目的。 相比传统启发式智能算法,GWO算法具有调整参数较少、结构简单、易于实现和优化性能好等特点。传统GWO算法的寻优结果与各等级狼的位置有极大关系,如果位置不理想,易陷入局部最优和过早收敛。
为了有效实现时滞下的翼型气弹系统控制,本文提出了一种基于双向随机灰狼优化算法和滤波Smith预估器的时滞控制方法,该方法设计了改进型滤波Smith预估器控制器,设计了双向随机灰狼优化算法,进行时滞下气弹控制参数的全局寻优,主要创新点包括以下3个方面:
(1)针对翼型气弹系统的有界时滞,设计基于双向随机灰狼优化算法和滤波Smith预估器的气弹控制方法,在时滞和多工况下保持气弹控制的良好动态特性;
(2)引入二阶滤波器,改进传统Smith预估器,增强时滞下的翼型气弹控制性能、在不确定时滞、系统变参数和干扰下增强鲁棒性和抗干扰能力;
(3)创新设计了双向随机灰狼优化算法(bidirectional random grey wolf optimization,BRGWO),来搜索时滞下气弹控制器的全局最优参数。 该算法通过改进不同社会等级灰狼的位置更新机制,增强狼群的多样性,提高跳出不理想位置的几率,避免陷入局部最优,从而提高全局最优值的寻优质量。
本文在通过以下算例对翼型气弹控制进行研究,即不确定时滞、固定时滞下的不确定工况(风速变化、结构刚度变化和负载干扰),将创新设计的BRGWO算法与传统智能优化算法进行对比,将本文方法与已有控制方法进行比较分析,验证其优越性和鲁棒性。
1 双向随机灰狼优化算法设计
1.1 传统灰狼优化算法
灰狼优化算法GWO是一种启发式种群智能优化算法,灵感来自于灰狼种群的狩猎和社会等级行为。狼群分为不同等级的四类,其中:α狼拥有最高等级并领导整个狼群,β狼尊重α狼并领导δ狼和Ω狼,δ狼只领导Ω狼。在传统灰狼优化算法中,α狼、β狼和δ狼一起领导Ω狼的狩猎行为,即优化过程。
灰狼种群的猎物包围策略为
D=|CXj(t)-μjX(t)|
(1)
X(t+1)=Xj(t)-A·D
(2)
(3)
式中:Xj猎物矢量位置;X灰狼矢量位置;A和C为系数矢量;μj为狩猎策略因子向量;rand1和rand2为0~1的随机向量;a为收敛因子;t为迭代次数;tmax为最大迭代次数。
α狼、β狼和δ狼的狩猎策略可表示为
(4)
1.2 双向随机灰狼优化算法的创新设计
本文首次创新设计了一种改进型的灰狼优化算法,即双向随机灰狼优化算法,其引入狩猎策略因子μ,采用基于狩猎策略因子矢量和系数矢量的双向随机机制来改进α狼、β狼和δ狼的狩猎方式,使得社会等级较高的狼能够跳出不理想的位置、寻找更多潜力位置,从而提高迭代后期的搜索能力、避免整个狼群陷入局部最优、避免算法过早收敛。
利用狩猎策略因子,BRGWO算法的α狼、β狼和δ狼的改进型狩猎策略可表示为
(5)
(6)
式中:μα,μβ和μδ分别为α狼、β狼和δ狼的狩猎策略因子向量;Dα,Dβ和Dδ分别为α狼、β狼和δ狼的包围步长向量;rand3,rand4和rand5为0~1的随机向量。
BRGWO算法的灰狼种群位置更新公式表示为
(7)
(8)
相比传统灰狼优化算法,创新设计的BRGWO算法具有以下优点:①利用式(7)~式(8)可对α狼、β狼和δ狼的狩猎策略进行不同程度的调节;②针对社会等级最高的α狼,采用较为保守的策略,在较小范围内增加狩猎包围的多样性;③针对社会等级第二优和第三优的狼,采用更加开放的策略,不断扩大狩猎包围的探索范围;④利用系数矢量和狩猎策略因子向量的双向随机机制,及时跳出α狼、β狼和δ狼的不理想位置,增强搜索能力、避免过早收敛和陷入局部最优。 BRGWO算法的流程如图1所示。

图1 BRGWO算法流程图Fig.1 Flow chart of BRGWO algorithm
2 翼型气弹系统
翼型气弹系统的结构示意如图2所示,其中包括来流风速、气动力、叶片弹性体和尾缘襟翼驱动器[23],翼型气弹系统的振动量为扭转角α和挥舞位移h,c为翼型弦长,b为半弦长,ab为中心点到弹力轴的距离,在气动力作用下的振动系统模型可表示为[24]
(9)
式中:mT为翼型气弹系统和支撑部分总质量;mW为翼型气弹系统质量;xa为质心和弹性轴之间无量纲距离;Iα为弹性轴转动惯量;ch,cα为阻尼系数;kh,kα为结构刚度系数;L,M分别为气动升力和气动力矩。
考虑定常气动力、振动位移以及尾缘襟翼驱动器对气动升力的影响,气动升力可表示为
(10)
式中:U为来流风速;clα为叶片攻角对应的气动升力系数;clβ为尾缘襟翼对应的气动升力系数。
考虑定常气动力、振动量以及尾缘襟翼驱动器对气动力矩的影响,翼型气弹系统承受的气动力矩可表示为
(11)
式中:cmα为攻角对应的气动力矩系数;cmβ为尾缘襟翼对应的气动力矩系数。
联合式(9)~式(11),翼型气弹系统的气动弹性模型可表示为
(12)
(13)

(14)
式中:控制量u为尾缘襟翼角β;τ为不确定时滞时间。本文控制目标为利用尾缘襟翼实现翼型气弹系统的扭转角和挥舞位移控制,根据经验,采用扭转角作为有效反馈量来实现控制目标。翼型气弹系统参数见Strganac等的研究。

图2 翼型气弹模型示意图Fig.2 Diagram of airfoil aeroelastic system
3 最优滤波Smith预估器设计
3.1 传统Smith预估器
传统Smith预估补偿器主要通过与控制器并联的补偿环节来补偿滞后时间,原理如图3所示[23]。

图3 标准Smith预估控制原理图Fig.3 Diagram of standard Smith predictive control
为了克服时滞环节exp(-Ls)的影响,控制结构中添加Gm(s)环节,对应闭环系统的特征方程可表达为
1+Gc(s)[Gm(s)+G(s)exp(-Ls)]=0
(15)
式中:G(s)为被控对象;Gc(s)为主控制器;Gm(s)为Smith预估补偿器。令Gm(s)=G(s)[1-exp(-Ls)] ,式(15)为
1+Gc(s)G(s)=0
(16)
由式(16)可知,经过时滞补偿后,由于exp(-Ls)在整个闭环特征方程之外,不会影响到系统稳定性,从而消除了滞后影响。但是,实际风力机叶片振动系统存在风速、刚度等不确定参数变化、时滞时间变化和负载干扰等影响,会使得G(s)和L发生不确定变化,导致模型失配;而传统Smith预估器对被控对象模型精度有较高要求,在模型失配下易严重的动静态误差,甚至使闭环系统变得非常不稳定,导致系统振荡;同时,翼型气弹系统由于本身颤振特性对于系统参数变化较为敏感,动态特性容易恶化,需要及时有效地克服模型失配并实现振动控制。
3.2 最优改进型滤波Smith预估器设计
针对不确定时滞和多变工况下的翼型气弹系统控制问题,设计基于二阶鲁棒滤波器的Smith预估控制,控制框图如图4所示。 其中:P(s)为控制对象;Gc(s)为主控制器;Gm(s)为Smith预估补偿器;F(s)为鲁棒滤波器;exp(-Lms)为纯滞环节;Y(s)为系统输出;R(s)为参考值;D(s)为驱动负载干扰。
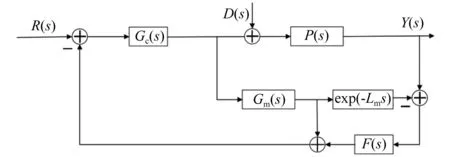
图4 滤波Smith预估控制结构图Fig.4 Diagram of filtered Smith predictive control
考虑翼型气弹系统中存在的有界时滞和不确定工况影响,被控对象可表示为
(17)
式中:ΔG为风力机工况下失配模型;ΔL为时滞变化量。
根据图4可知,单输入单输出闭环系统的传递函数可表示为
(18)
式中,Pm(s)=Gm(s)exp(-Lms)为理想系统模型。
针对翼型气弹系统,设计主控制器Gc(s)为PID控制器
(19)
传统方法多采用一阶滤波器,本文基于滤波参数λ,设计二阶鲁棒滤波器为
(20)
(1)当无系统变化、无时滞时间变化时,存在G(s)=Gm(s),L=Lm,即P(s)=Pm(s),由式(9)可知,闭环系统的特征方程可简化为
1+Gc(s)Gm(s)=0
(21)
(2)当存在不确定时滞和不确定系统参数变化的工况下时,G(s)≠Gm(s),L≠Lm,即P(s) ≠Pm(s)。 根据式(9),闭环系统的特征方程可表示为
1+Gc(s)Gm(s)+Gc(s)F(s)[G(s)e-Ls-Gm(s)e-Lms]=0
(22)
利用式(20),设计滤波Smith预估器为
(23)
将式(17)代入式(23),滤波Smith预估器可变为
(24)
将式(23)代入式(22),得闭环系统特征方程
1+Gc(s)G(s)=0
(25)
由式(21)和式(25)可知,根据设计的主控制器和滤波Smith预估器,在理想情况、时滞变化和多变工况下可在闭环系统的特征方程中消除时滞环节,从而消除时滞对翼型气弹控制系统的影响。式(23)和式(24)可知,所设计滤波Smith预估器可以针对模型失配和时滞变化利用鲁棒滤波器F(s)进行控制。通过获取主控器参数和滤波参数的最优值,可以最大程度上优化不确定时滞和工况下的振动控制效果。
(3)驱动负载干扰对系统输出影响的传递函数可表示为
(26)
高阶翼型气弹系统可等效为二阶阻尼系统
(27)
式中,a2,a1,a0,b1,b0为传递函数系数,均为正值。
将式(19)和式(20)和式(27)代入式(28),整理后可得负载干扰下的闭环系统特征方程
(λs+1)2[(a2+kdb1)s2+(a1+kpb1-kdb0)s+
(a0-kpb0+kib1)]=0
(28)
由式(28)可知,通过选择合适的主控器参数(kp,ki,kd)可以保证干扰下的闭环系统稳定性;通过设计合适的滤波参数λ可进一步优化时滞气弹控制的动态特性和抗扰性能。
3.3 闭环稳定性证明
利用最小增益原理,对所设计闭环系统的稳定性进行证明。假设无时滞的翼型气弹系统G(s)为稳定系统,主控制器Gc(s)和滤波器F(s)也保持稳定。 图3中闭环系统具有稳定性的充分必要条件为
|Gc(s)|H+|Gc(s)||F(s)||ΔP(s)|<1
(29)
式中:ΔP(s)为模型失配;H为模型失配的上界。
|ΔP(s)|=|P(s)-Pm(s)|<1
(30)
根据式(19)和式(20),存在
|Gc(s)|<‖Gc(s)‖∞,|F(s)|<‖F(s)‖∞
(31)
将式(30)和式(31)代入式(29),整理后可得
‖Gc(s)‖∞|ΔP(s)|(1+|F(s)|)<1
(32)
式(32)可进一步整理为
(33)
由式(33)可知,当翼型气弹系统的模型失配上界为1/[‖Gc(s)‖∞(1+‖F(s)‖∞)]时,所设计基于滤波Smith预估器的闭环控制系统具有稳定性。
推论1当系统参数变化,时滞时间不变时,存在G(s)≠Gm(s),L=Lm,模型失配可表示为ΔP(s)=[G(s)-Gm(s)]e-Ls=ΔG(s)e-Ls,代入式(33)可得系统参数变化下的闭环系统稳定条件为
(34)
推论2当时滞时间变化,系统参数不变时,存在G(s)=Gm(s),L≠Lm,模型失配ΔP(s)可表示为
ΔP(s)=G(s)(e-Ls-e-Lms)≈
G(s)(Lm-L)s=G(s)ΔLs
(35)
代入式(33)可得时滞时间变化下的闭环系统稳定条件为
(36)
3.4 时滞下最优气弹控制参数整定
针对基于改进型滤波Smith预估器的翼型气弹控制器,利用所设计的BRGWO算法计算最优控制参数,获取最优气弹控制器,在不确定时滞、不确定风速、刚度变化和驱动干扰4种算例下进行控制试验。控制参数优化计算的目标函数为
(37)
气弹控制器参数kp,ki,kd,μ取值范围分别为[-50,0],[-50,0],[-10,0]和[0,2]。襟翼角的限制为[-60°,60°],时滞时间不超过3 s。灰狼种群规模30,最大迭代次数30。为了验证所设计BRGWO算法的优越性,采用遗传算法(genetic algorithm,GA)和灰狼优化算法进行对比试验,为了公平起见,GA算法和GWO算法的种群规模和最大迭代次数也为30。目标函数的适应度值优化结果如图5所示。可见,GA和GWO容易陷入局部最优,而BRGWO算法显著改善了控制参数的全局寻优性能、具有更快的收敛性,有效避免了局部最优。基于BRGWO算法和滤波Smith预估器的翼型气弹系统控制结构如图6所示。

图5 目标函数的适应度值Fig.5 Fitness value of objective function

图6 基于BRGWO算法和滤波Smith预估器的翼型气弹系统控制结构图Fig.6 Control structure of aeroelastic system based on BRGOW algorithm and filtered Smith predictor
4 仿真算例
本文采用所设计的BRGWO算法和改进型滤波Smith预估器,应用于不确定时滞下的翼型气弹控制、以及多工况下的翼型时滞气弹控制研究。翼型气弹系统参数参见文献[26]。系统时滞为1 s,选择风速值U=6 m/s,刚度参数kα=2.82 N/m,kh=2 844.4 N/m。仿真在2.9 GHz IntelR CoreTMi7 CPU和16 GB RAM配置的计算机上执行,仿真采用MATLAB/Simulink 2020a环境。 为了研究本文方法 (BRGWO-MF-Smith),对比了GWO优化的经典Smith预估控制(GWO-Smith)、GWO优化的PI-PD型Smith预估控制(GWO-PIPD-Smith)、GWO优化的一阶滤波Smith预估控制(GWO-F-Smith)。各控制器参数的优化计算结果如表1所示,气弹控制效果如图7所示。可见,已有经典Smith预估控制和传统GWO算法难以克服时滞的不利影响,气弹控制响应存在较大超调量、较长稳定时间,尾缘襟翼的驱动劳损也较大;而本文提出的改进型滤波Smith预估器和BRGWO算法,显著改善了系统超调量、稳定时间和驱动劳损,在4个控制器中具有优越性。

表1 各控制器的最优控制参数

图7 翼型时滞气弹控制效果Fig.7 Delayed aeroelastic control
4.1 不确定时滞下气弹控制
为了研究不确定时滞下的翼型气弹控制效果,针对时滞时间+20%,+50%的两种案例进行了试验,翼型时滞气弹控制效果如图8和图9所示。可见,GWO-Smith难以适应时滞时间的不确定变化,存在控制性能急剧恶化及系统失稳现象;GWO-PIPD-Smith和GWO-F-Smith可在不确定时滞下保持系统的稳定性,但存在较大超调量或较长稳定时间。然而,本文提出的BRGWO-MF-Smith时滞气弹控制方法,在不确定时滞下,显著减小了超调量、缩短了稳定时间、降低了襟翼控制成本,对比其他3种方法在不确定时滞下具有较强的鲁棒性。

图8 时滞时间+20%下的翼型气弹控制效果Fig.8 Delayed aeroelastic control under delay time+20%
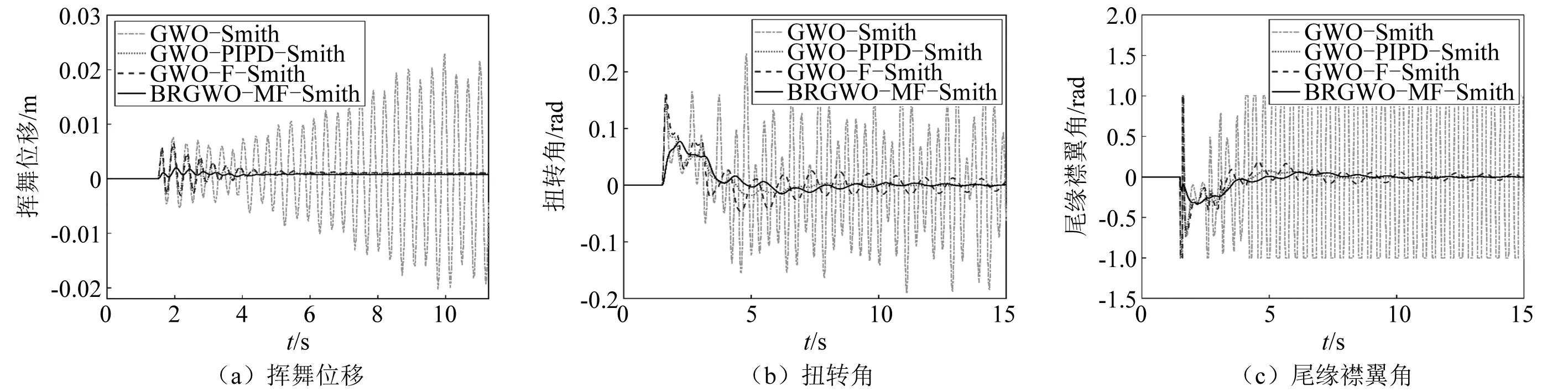
图9 时滞时间+50%下的翼型气弹控制效果Fig.9 Delayed aeroelastic control under delay time+50%
4.2 不确定风速下时滞气弹控制
为了验证本文方法在不确定风速下的时滞气弹控制效果,分别研究了风速变化+20%和-20%的工况,系统时滞时间为1 s,时滞气弹控制响应如图10和图11所示。可见,出现较大风速时,GWO-Smith无法在短时间内实现气弹控制。然而,相比GWO-PIPD-Smith和GWO-F-Smith,本文方法可以最小超调量和最少振荡来实现气弹系统的颤振抑制,针对风速变化保持了良好的时滞气弹控制效果。 仿真结果说明了不确定风况下BRGWO-MF-Smith在4种控制器中具有最强的时滞气弹控制效果和鲁棒性、以及最小的驱动劳损。

图10 风速+20%下的翼型时滞气弹控制效果Fig.10 Delayed aeroelastic control under wind velocity+20%
4.3 刚度变化下时滞气弹控制
为了验证本文方法在系统刚度参数变化下的有效性,分别研究了挥舞刚度和扭转刚度+20%和-20%两种案例,时滞气弹控制响应如图12和图13所示,气弹系统对刚度变化较为敏感,在此情况下,GWO-Smith无法保证系统的稳定性、难以实现有效的气弹控制;PIPD-Smith的超调量较大、GWO-F-Smith的稳定时间较长;而本文设计的BRGWO-MF-Smith方法明显改善了超调量、大幅缩减了稳定时间,在不同刚度变化下保持了良好的鲁棒性和较小的驱动劳损。因此,本文方法具有最佳的翼型时滞气弹控制性能。
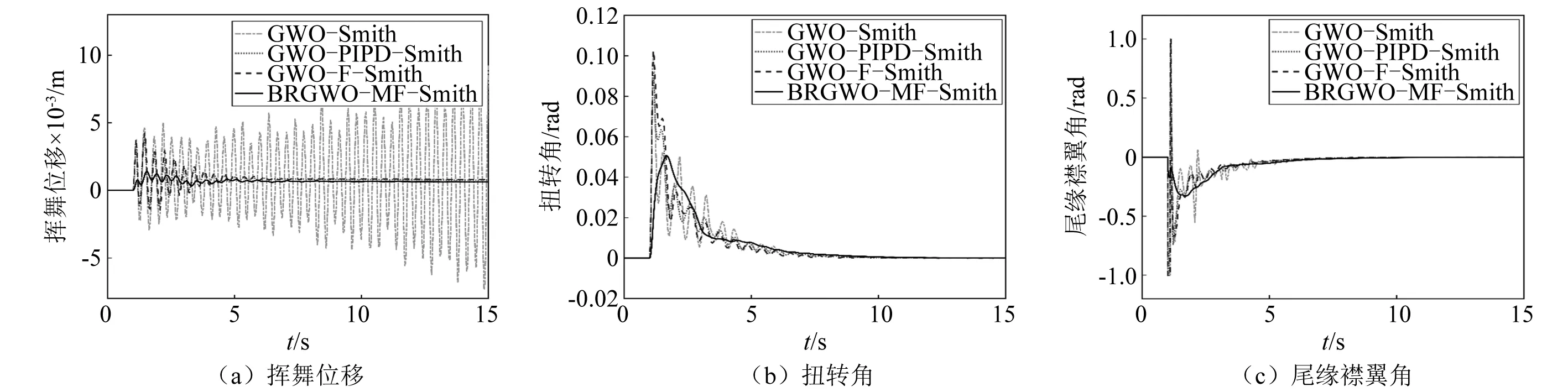
图11 风速-20%下的翼型时滞气弹控制效果Fig.11 Delayed aeroelastic control under wind velocity-20%
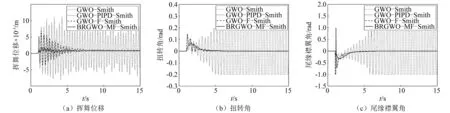
图12 刚度+20%下的翼型时滞气弹控制效果Fig.12 Delayed aeroelastic control under stiffness+20%
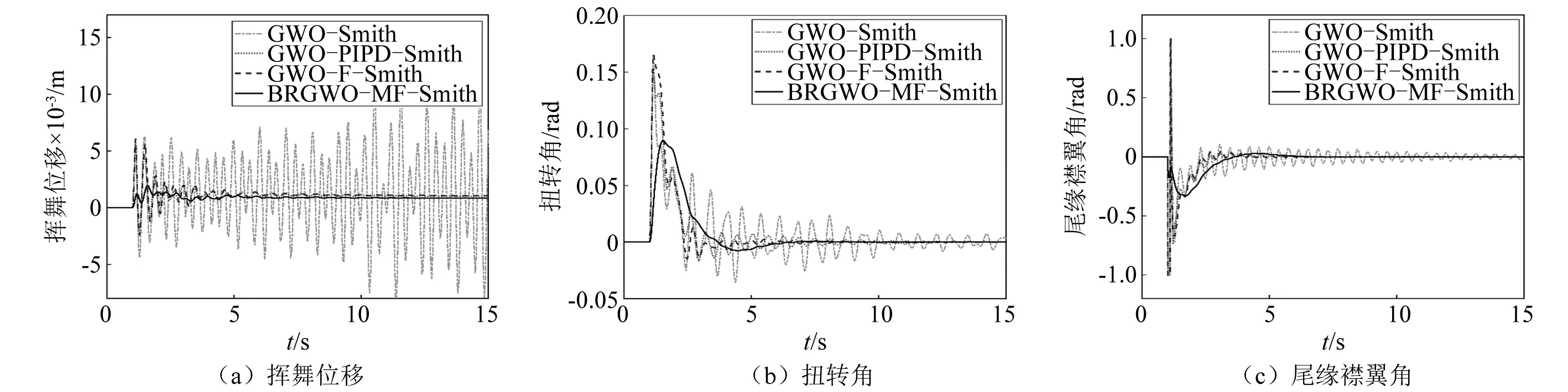
图13 刚度-20%下的翼型时滞气弹控制效果Fig.13 Delayed aeroelastic control under stiffness-20%
4.4 驱动干扰下时滞气弹控制
在实际中还需要考虑来自驱动器的负载干扰,在6 s处加入驱动负载干扰信号,干扰下的翼型时滞气弹控制响应如图14所示。可见,4种控制器都可以克服驱动干扰,但GWO-Smith仍无法在短时间完全抑制系统颤振,PIPD-Smith和GWO-F-Smith存在较大超调量尖峰和较多振荡。对比这些控制器,本文BRGWO-MF-Smith方法的时滞气弹控制具有最佳动态性能、更优越的抗扰性能和襟翼驱动性能。
4.5 定量分析
针对4种气弹控制方法,表2和表3分别给出了7种算例下挥舞位移和扭转角的绝对误差积分指标(integral of absolute error,IAE)。 可知,本文方法在所有7种算例下均具有最小的挥舞位移IAE值和扭转角IAE值。在时滞+50%算例下,BRGWO-MF-Smith控制下的扭转角和挥舞位移IAE值,对比GWO-Smith控制改善了86.5%和90.9%,对比PIPD-Smith控制改善了10.1%和26%,对比GWO-F-Smith控制改善了51%和31%;在风速+20%算例下,本文BRGWO-MF-Smith的挥舞位移IAE值,对比GWO-Smith,PIPD-Smith和GWO-F-Smith,分别改善了90.2%,33.9%和39.7%;在刚度-20%算例下,对比3种已有控制器的扭转角IAE值分别改善了43.5%,26.6%和23%; 在干扰算例下,改善了3种已有控制器的挥舞位移IAE值得分别为57.3% 26.5%和30.4%。这得益于本文创新设计的BRGWO算法和改进型滤波Smith预估器,针对气弹系统具有更为优良的时滞控制补偿效果、可有效寻找全局最优的时滞气弹控制参数。

图14 驱动负载干扰下的翼型时滞气弹控制效果Fig.14 Delayed aeroelastic control under load disturbance

表2 7种算例下翼型时滞气弹控制的挥舞位移IAE性能指标
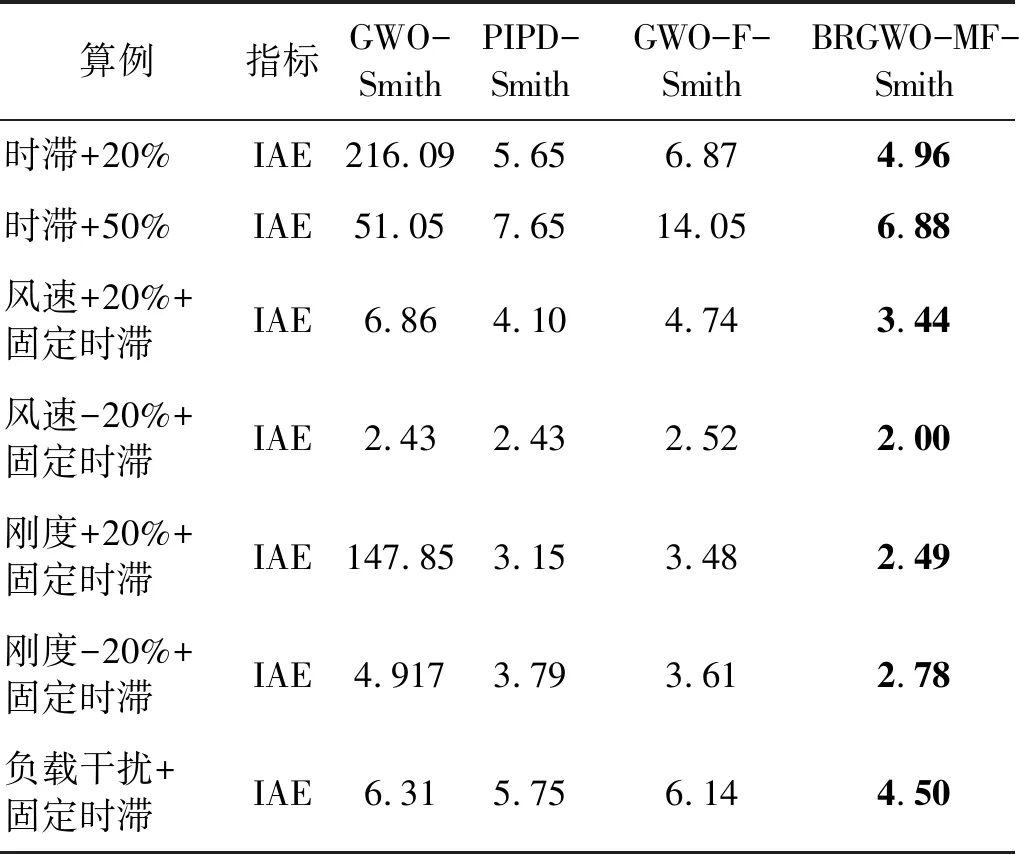
表3 7种算例下翼型时滞气弹控制的扭转角IAE性能指标
5 结 论
本文设计了基于二阶滤波Smith预估器的翼型时滞气弹控制结构,利用本文创新设计的双向随机灰狼优化算法寻找全局最优控制参数,在不确定时滞和多种工况算例下取得了良好的时滞补偿效果和气弹控制效果。主要结论归纳为以下3个方面:
(1)基于Smith预估控制理论,构建了时滞下翼型气弹系统的控制器,引入二阶鲁棒滤波器改进Smith控制结构,增强了不确定时滞下气弹控制的动态性能和鲁棒性。
(2)基于分级制定包围狩猎策略的思想,创新设计了双向随机灰狼优化算法,避免了陷入局部最优、增强了全局最优值的搜索能力、加快了收敛速度,提高了翼型时滞气弹控制参数的全局寻优能力。
(3)仿真结果表明,基于BRGWO算法和改进型滤波Smith的翼型最优气弹控制器,对比已有算法及控制方法,在不确定时滞下显著改善了气弹控制效果,在不确定风速、刚度变化和驱动干扰下,具有优越的是时滞补偿能力和气弹控制性能,鲁棒性较强。
