数形巧结合，培养学生解决问题能力

厉志敏

【摘 要】小学生的思维仍以形象思维为主，而数学的特质决定了这是一门抽象的学科。所以在教学中，我们需要培养学生的抽象思维。数形结合思想便是引导小学生由形象思维转向抽象思维的桥梁。数形巧结合，在帮助学生理解题意解决问题的同时，学生的抽象思维逐步形成，数学能力得以发展。基于此，本文主要介绍了利用数形巧结合来培养学生解决问题能力的必要性，提出了利用數形巧结合来培养学生解决问题能力的有效策略。

【关键词】数形结合;解决问题能力;学生;培养

数学，简单来讲，探究现实世界数量关系以及空间形式的科学。在数学中主要概念体现在两个方面，一方面是数，另一方面是形，是数学发展的重要基础。在客观世界中数与形有着密切的联系。数形结合的思想方式是两个条件决定，一是客观现实，二是数学。尤其是小学学生，其是以形象思维为主，在数学教学过程中要想培养分析问题能力以及解决问题能力，就必须要重点培养学生的数形结合思想，应该有针对性和目的性对学生开展数形结合训练，提高学生学习效率，培养其数学素养。

一、利用数形巧结合来培养学生解决问题能力的必要性

在小学数学教材中涉及到很多数学公式和数学定义，有些学生难以准确理解题意，不能正确解决问题。而数学问题中最为关键的是数和形复杂，倘若学生在分析问题中学会将数与形相结合，这样必定可以事半功倍，帮助学生迅速准确理解题意。因此，作为小学数学教师，在教学过程中不能将数和形当作各自独立的个体，这样不便于学生正确审题解决问题。而应该不断创新和改变，引导学生尝试着将数和形相结合。为了可以进一步提高学生学习效率，教师应该在教学中合理运用各种策略，使学生理解数形结合的方法。数形巧结合，在帮助学生理解题意解决问题的同时，学生的抽象思维逐步形成，进而提高数学学习力，数学素养得以发展。

二、利用数形巧结合来培养学生解决问题能力的有效策略

在小学数学教学中培养学生解决问题能力的途径有多种，其中，数形结合思想是我们一线教师常用的方法，数与形巧妙结合，逐步脱离形象思维到抽象思维，教学效果更加显著。

（一）以形助学

在小学数学教学中很多教师通过图形的直观性使学生掌握数的概念、将数的规律揭示出来、明确数量之间的关系，解决学生认识数的抽象性的问题，有利于学生准确理解数，掌握数量关系，使数学问题得到有效解决。

1.利用图形认识数

不管是认识分数还是整数，都能够利用图形来掌握计数单位以及数的构成，加强学生数感。在认识负数过程中教师可以采用该教学方法，首先要求学生在竖直放置的温度计模型上将零摄氏度的部位清楚标注，再将这些温度标注出来，分别是13摄氏度、5摄氏度、零下6摄氏度、6摄氏度、7摄氏度。学生通过观察发现，得出这样的结论：将0度当做分界线，朝着上面，表示温度高，反之，朝着下面，表示温度低。接着，教师将温度计朝着下端按照顺时针方向旋转90度，便是平放的温度计，将该温度计右端加上相对应的箭头，即数轴。如图1所示（单位是摄氏度）

图1  平放的温度计示意图

从图中学生可以发现，将0当做分界线，左边和右边分别是负数、正数，从左到右数不断变大，从右到左数量不断变小。学生利用数轴以及温度计对正负数有准确的认识，对正数和负数的大小进行对比，构建数和形之间的联系，掌握负数的真正意义。

2.借助图形掌握算理

3.借助图形掌握统计和概率的意义

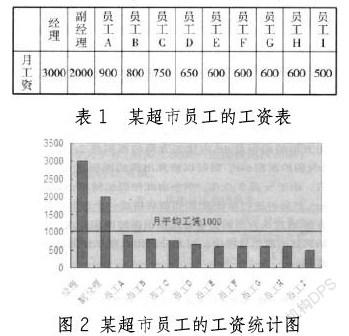
在统计中部分改变，比如：平均数，还有中位数等等，学生很难将其意义充分掌握，在教学过程中能够借助图形进行理解。将中位数以及众数概念引进时，首先教师可以合理创设该情境：小明从学校毕业后到超市应聘工作，超市的应聘广告上这样写到“本超市收银员平均工资2000元。”但是小明工作一个月后实际领取的工资只有1800，那是为何呢？小明找到超市的经理，经理将小明的当月工资单（表1所示）拿出来后。小明经过计算，工资平均有1000元，没有什么问题。那么，请问这里每个月平均工资就是指月工资水平吗？如果统计表不具有直观性。教师可以鼓励学生尝试着画出统计图（如图2所示），将问题直观的解释出来。

学生通过对图2 进行仔细观察，发现很多人的工资都比2000低，只有副经理以及经理的工资超过2000。这就表示该题目中平均数因为受到一些极端数据产生的影响而无法将员工的普通水平表示出来，由此感受到将中位数以及众数引进到课本中十分有必要。并且在开展抛硬币实验时，教师可以要求学生以小组的形式开展实验，将实验中硬币抛出正反面的概率制作成一个折线统计图，学生观察得出，全部数据都约0.5。这就表示硬币不管是抛出正面还是反面，可能性都是一样的。利用条形图以及折线统计图，让学生可以直观认识概率以及统计的意义，也可以对数据进行全面分析，将现象以及事件的大概发展方向科学预测出来。

（二）以数辅形，将模糊转变成清晰

在教学过程中教师往往借助数的准确性使学生掌握关于形的知识，主要包括位置，还有运动变化等等，而且对形的体积以及长度等等进行测算。

1.借助数找到形的特点

一般来说，只是利用个人的直觉想要找到图形的特征，这是非常困难的。在实际教学过程中教师应该鼓励学生利用深入探究数找到形的特点。比如：对《三角形三边的关系》进行讲解时，教师先要将四组小棒展示在学生面前，引导学生尝试着将小棒围起来，看看是否可以围成三角形。学生利用亲自操作后，得出第一组和第二组小棒可以围成三角形，第三组和第四组小棒不能围成三角形。这究竟是什么原因呢？很多学生猜想很有可能与这三边长度有一定的关联。是否存在关系，又有哪些关系呢？接着，教师将各小组的实际长度告知学生。学生利用自己思考以及小组沟通得出，可以围成三角形的三条边都有相同的点，即两条边的和必定比第三条边大。而无法围成三角形的三条边中往往都是两条边的和小于第三条边或者等于第三条边。通过数据的准确性找到图形的特征，这样可以加深学生对图形的认识以及理解。

2.借助数确定形的部位

物体的部位使用文字进行描述通常都非常繁琐复杂，也不具有较强的准确性。比如：对《确定物体的位置》进行讲解时，首先教师将座位圖展示给学生看，要求学生讲讲小红、小明和小李的座位。学生用很多语言进行描述，小红是右起第二组的第6个位置，小明是右起第二组的第4个位置以及小李是左起第一组的第3个位置。然后，教师将坐标图抽出来，这样学生就可以使用数将同学的座位表示出来。将文字描述转变成数对描述，学生可以深刻感受到数对的简洁性以及准确性。实际上，在日常生活有许多数都可以对物体部位进行描述，比如：能够利用经度以及纬度表示出在地球仪上某个地区的位置。通过数的特性使物体位置得到精确的描述，这样学生可以感受到以数辅形的作用。

3.利用数对形的大小估测

形具有较强的全面性以及直观性，然而画上的形的精确性，由于图形能够结合需求根据一定的比例进行缩小和放大。然而只要利用数，人们就可以迅速准确测算形的长度以及面积。比如：对《圆的面积》进行讲解时，教师能够创设该问题情境：一个喷水龙头的最远射程为5米，求出其转动一周可以浇灌的面积。其实，这就是将半径是5米的圆的面积求解出来。然而此时学生尚未学习圆的面积计算公式，首先应该估算。教师要求学生在方格纸上将半径是5米的圆画出来，再将圆的内接正方形以及外切正方形画出来。学生求出外切正方形的面积为10×10=100（平方米），内接正方形面积为10×5÷2×2=50（平方米），该圆的面积估算在50-100平方米。若将方格取消，可以用r表示圆的半径，那么，外切正方形和内接正方形的面积分别为4r2和2r2，获得2r2<圆的面积<4r2，这样一来，就能推算出圆的面积约3r2。因为π为3点多，学生可以大胆提出相应的猜想，S圆为πr2。接着验证：对圆进行切割，拼装成近似的长方形，利用长方形的面积公式将圆的面积公式正确推导出来。对该教学片段进行估算时，能够充分利用数据对圆的面积正确估测。

三、结束语

总而言之，学生在小学阶段就感受到学习数学带来的趣味性，培养学生发现问题能力、分析问题能力和解决问题能力，使学生的学习状态从原来的被动接受转变成主动学习，使学生形成良好的数学素养，在小学数学教学中将素质教育全面落实到位。

【参考文献】

[1]贾爱萍.数形结合，培养学生解决问题的能力[J].新课程导学，2014（35）：46.

[2]贡红华.数形结合，培养学生的问题解决能力[J].启迪与智慧（教育），2013（04）：22.

[3]吴赞棠.数形巧结合，求解高考题[J].数学教学通讯，2010（18）：51-52.

[4]游琼英.数形结合：培养学生解决问题的能力[J].教育科学论坛，2009（10）：52-54.

[5]蒋丽卿.数形结合——培养学生的问题解决能力[J].学生之友（小学版）（上半月），2009（10）：44.