基于信息粒化与支持向量回归机的内河船舶油耗预测

2021-12-17童亮陈雪梅郑朋飞

船海工程 2021年6期

童亮，陈雪梅，郑朋飞

(重庆交通大学航运与船舶工程学院，重庆 400074)

由于不断增长的航运需求，船舶温室气体排放量预计将在2050年前较2018年增加50%[1]。因此，作为《船舶能效管理计划》(ship energy efficiency management plan，SEEMP)的重要组成部分，越来越多的国际规则的制定已集中于船舶能源效率的提高。在船舶实际运营过程中，燃油费用占运营总成本的30%～60%[2]，而内河船舶多变的通航环境使其油耗过程更具复杂性。因此，在一定的航程和有限的时间内使船舶油耗最低是我国内河航运业技术改造和产业升级迫切需要解决的重要问题之一。

船舶油耗预测的建模方法可分为：理论公式建模和统计数据建模。理论建模，模型的建立需要完整的船舶设计参数和实验数据，分析过程中涉及环境因素过多且建模难度相对较大[3-4]，因此理论公式建模无法囊括所有船型，实用性需进一步提高。统计数据的建模主要通过分析船舶油耗相关因素，将数学方法和机器学习相结合，摈弃冗杂的机理分析，建立实测数据的预测模型，准确度高，实用性好。

因此，针对复杂的能耗特征和多变的内河环境，考虑以内河某散货船为例，对目标船舶安装多个传感器测得实船数据，采用多个模型(SVR模型、BP模型和ELM模型)分别对油耗进行预估，对比分析网络模型对实船油耗的预测结果；利用支持向量回归机(support vector regression,SVR)与模糊信息粒化(fuzzy information granulation,FIG)结合的方法对船舶未来一段时间内的油耗进行回归于预测分析。

1 内河船舶能耗主要影响因素

内河运输节能降耗面临着以下问题[5]：①量大面广，船型杂乱；②船龄偏老，信息化不高；③管理水平低较，运输效率有待提高；④能耗管控不力，综合油耗相对偏高，排放高。列举影响船舶油耗的主要因素见表1。

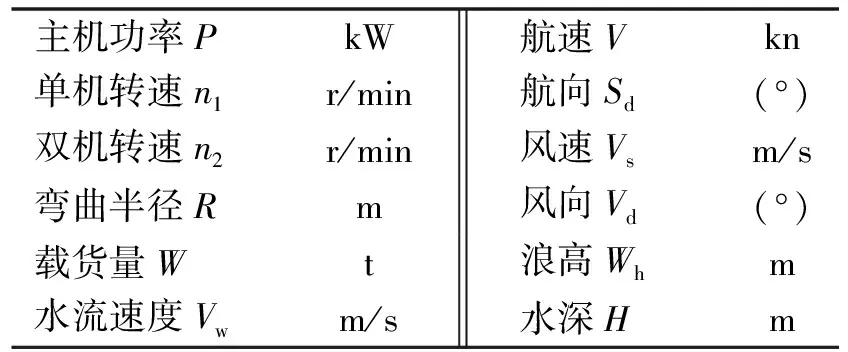
表1 影响船舶油耗的主要因素

2 数据预处理

船舶航行时，系统采集到的多维数据具有样本大、准确度低的特点。为了得到精准的预测模型和有效的预测结果，通常使用区间缩放法将输入数据、输出数据线性压缩至[0，1]区间内的量纲值，以消除多维数据不同量纲的影响。归一化处理见下式[6]。

(1)

式中：x*为归一化处理后的数据；x为输入数据；xmax为输入数据最大值；xmin为输入数据最小值。

模型的输入参数众多，变量之间有一定的相互作用和关联性。因此，采用主成分分析法(principal component analysis，PCA)对变量进行降维处理，提取影响油耗的关键特征。

Fp=a1i·ZX1+a2i·ZX2+…+api·ZXp

(2)

式中：FP为影响油耗的主成分；a1i,a2i,…,api(i=1,2，…,m)为输入变量的协方差阵Σ对应的特征向量，ZX1,ZX2,…,ZXp为输入变量的标准化值。

3 组合预测模型

3.1 SVR模型

在航船舶的燃油消耗时间序列具有较强的非线性和随机性，采用SVR模型对船舶油耗进行预测，该模型具有以下优势[7]：①SVR模型得到的是理论上的全局最优解，可避免局部最优问题；②SVR模型通过非线性变换将原始变量映射到高维特征空间构造线性分类函数，既可保证模型的良好泛化能力，又可解决向量“维数灾难”问题。模型中关于油耗预测的非线性回归问题的寻优实施步骤为：

1)在高维特征空间建立线性回归函数。

f(x)=wΦ(x)+b

(3)

式中：Ф(x)为非线性映射函数。

2)定义ε线性不敏感损失函数。

(4)

式中：f(x)为预测值；y为对应的实际值。若预测值与实际值之间的差值小于等于ε，则损失为0。

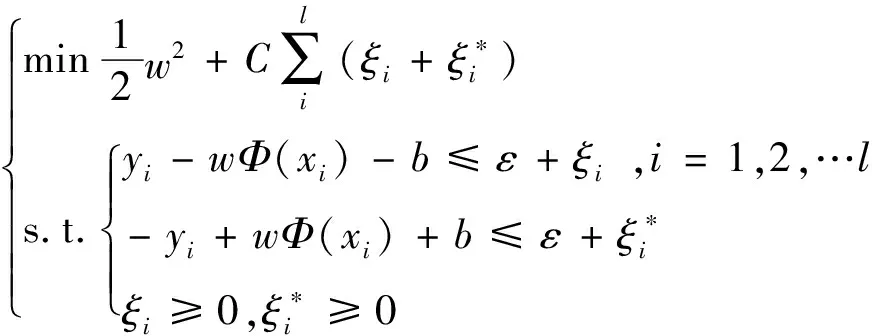
(5)

式中：Ф(x)为非线性映射函数，C为惩罚因子，ε规定了回归函数的误差要求。

f(x)=w*Φ(x)+b*=

(6)

选取径向基核函数

K(xi,xj)=Φ(xi)Φ(xj)

(7)

5)带入核函数，求解回归函数。

f(x)=w*Φ(x)+b*=

(8)

3.2 模糊信息粒化

传统油耗预测模型只对数据进行预处理，未对其影响因素进行特征分析，使得预测结果不精确、波动性大；预测大多停留在点时间上，忽视了对油耗一段时间内的波动情况和变化范围。因此，通过信息粒化(information granulation, IG)对大量油耗数据的内部特征进行分析，将整体划分为个体。

FIG将油耗数据划分成2 h一个窗口并对其模糊化处理，选用三角型的模糊粒子在窗口上建立模糊集，代替原窗口数据，使实船油耗数据中不确定的变量转换成确定数值，很好地解决了模糊数中无法准确度量只能模糊处理的矛盾。三角型隶属函数如下。

(9)

式中：x为输入的时间变量；a、m、b分别为输入数据粒化后的最小值Low、平均值average和最大值Up。

3.3 算法实现流程

基于模糊信息粒化的SVR组合预测模型的流程见图1。

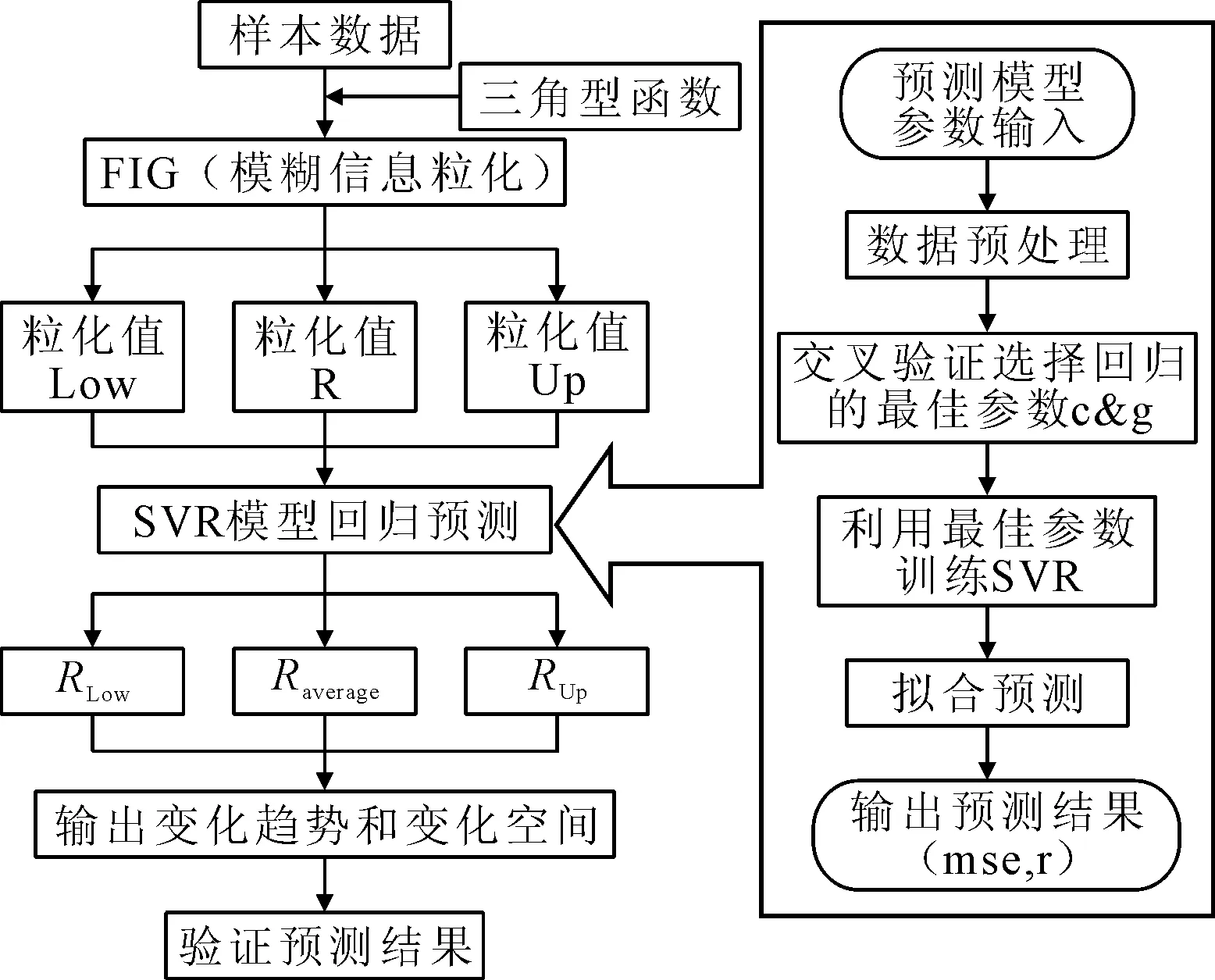
图1 基于模糊信息粒化的SVR组合模型流程

运用三角型函数对记录的油耗时序值进行FIG处理，得到粒化值Low、R、Up，利用SVR模型对粒化后的数据进行回归预测，得到预测的每个窗口油耗范围RLow、Raverage和RUp，将预测数据与实际数据的变化趋势和变化范围进行比较，验证模型预测效果。

4 实例验证

4.1 研究对象

以长江某散货船为研究对象，该轮主要参数和主机相关参数见表2。

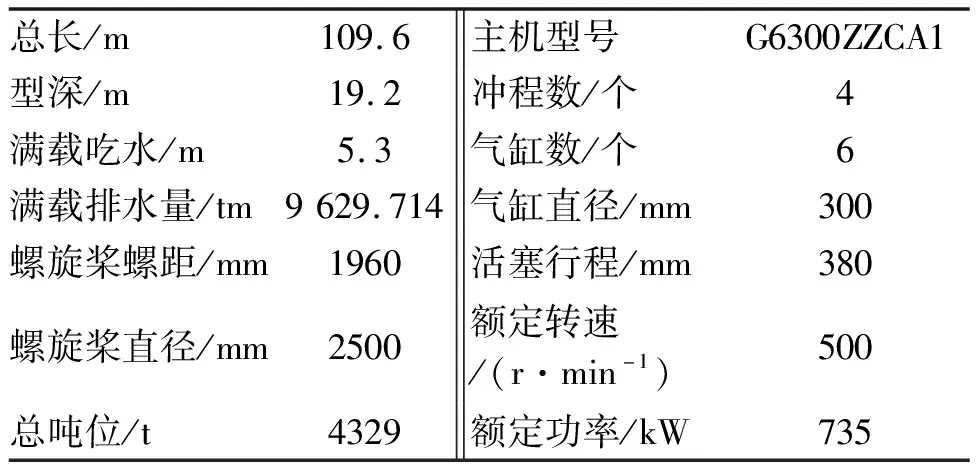
表2 目标船舶主要参数

4.2 PCA处理

运用PCA对表1中的油耗相关参数进行分析，得到10个主成分的特征值、贡献率。通过式(2)，计算主成分与相关参数的对应关系，得到各参数的主成分贡献率见表3。

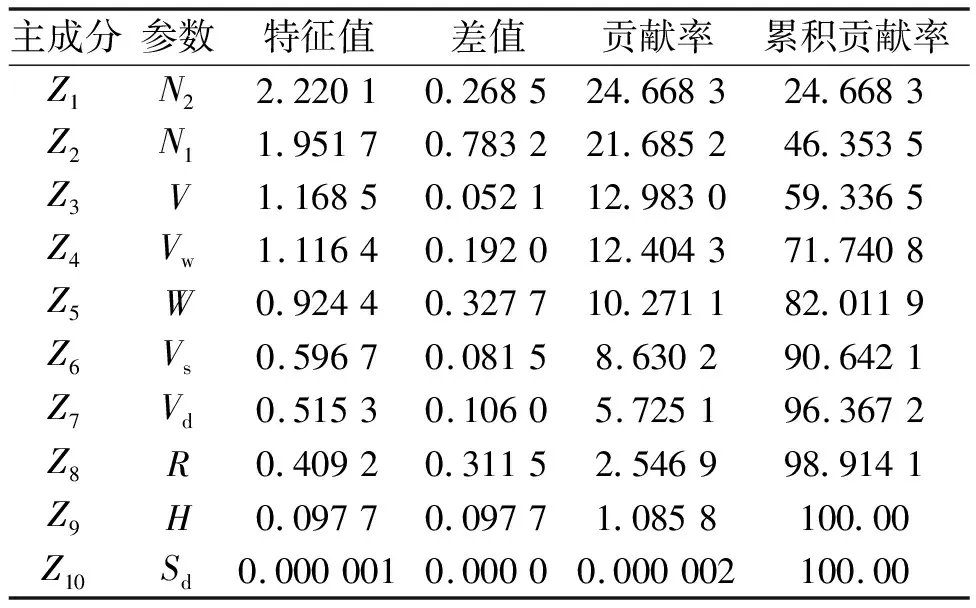
表3 相关参数主成分贡献率

从表3知，Z1～Z7的累积贡献率达到96.367 2%，Z8～Z10的贡献率则很小。因此，油耗预测模型的输入维数降为以下7维：双机转速n2、单机转速n1、航速V、水流速Vw、载货量W、风速Vs、风向Vd。

4.3 多个预测模型对比

选取目标船舶江阴-南家坨航次，总计1 320组上水航行数据，以每30 min内主机累积消耗的燃油作为分析对象。为不失一般性，采用随机的方法产生1 000组数据作为训练集和320组数据作为测试集分别对模型的性能进行评价。按照时间序列的燃油消耗数据集见图2。

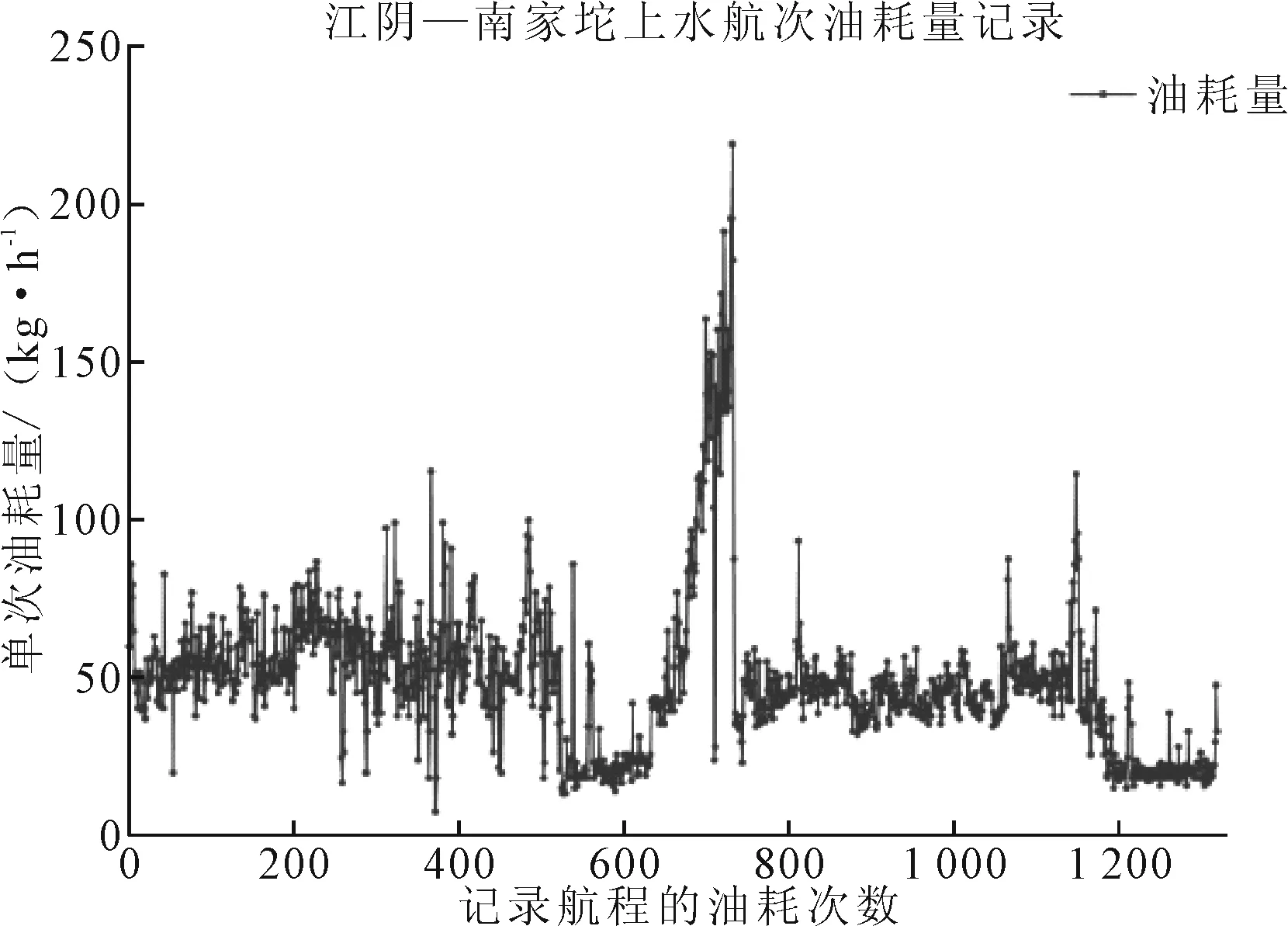
图2 目标船舶燃油消耗时间序列

观察图2燃油消耗时间序列，可知油耗波动起伏明显，多个无序的峰值给预测带来了难度。运用SVR模型对数据集进行预测，过程如下：首先对输入的多维参数作归一化处理，默认核函数为径向基核函数(RBF)，采用交叉验证的方法寻找中间参数C(惩罚因子)和参数g(RBF核函数中的方差)，运用GS算法得到精细寻优的最佳C和g来训练SVR模型，记录输入参数的回归预测值，输出真实值与预测值的对比结果。本次精细寻优下的最优参数bestC=16，bestg=0.250 0，数据集的预测结果见图3、4。

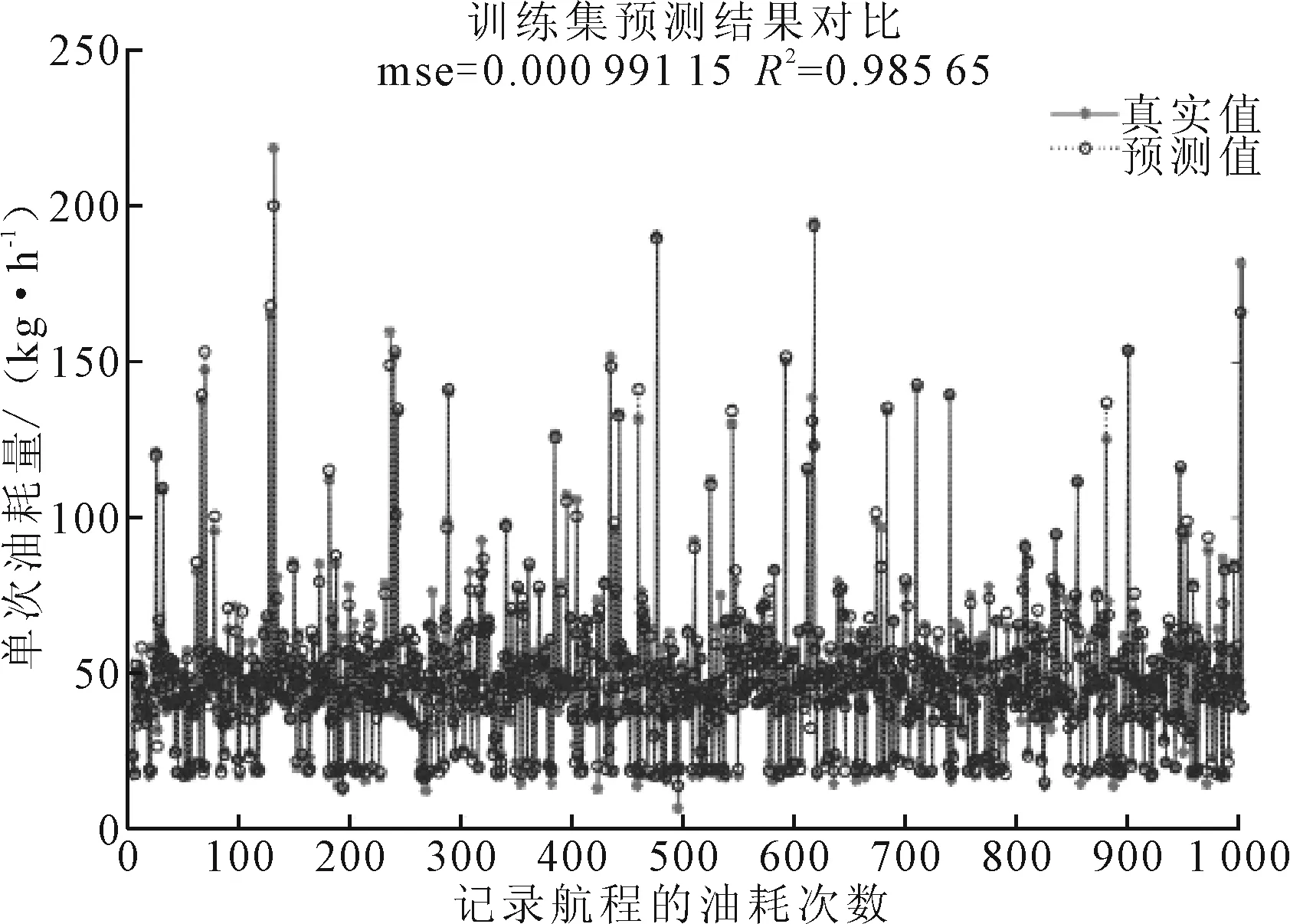
图3 SVR训练集预测结果

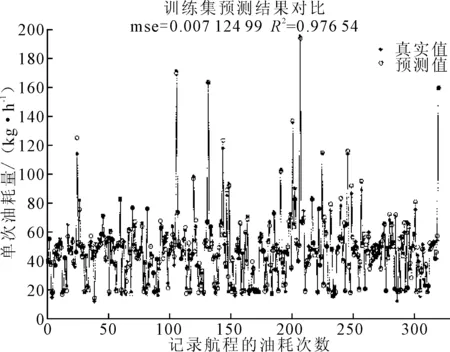
图4 SVR测试集预测结果

由图3、4所示，SVR模型训练集和测试集的均方误差分别为0.000 991 15和0.007 124 99，决定系数分别达到0.985 65和0.976 54。这表明，所建立的SVR油耗回归模型具有非常好的泛化能力，预测效果良好。

对320组测试集分别运用BP模型、ELM模型进行预测。BP模型参数设置如下：最大训练次数为1 000、训练要求精度为10-3、学习率为0.1；ELM模型的激活函数为sigmoid、隐含层神经元个数为7、性能函数为mse。测试集的预测结果见图5、6。

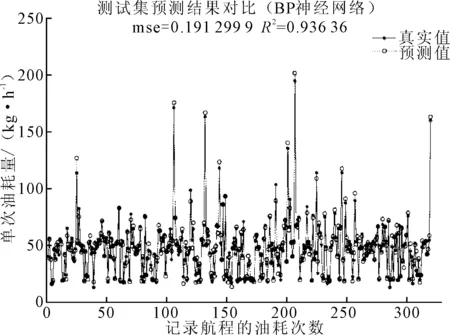
图5 BP模型测试集预测结果

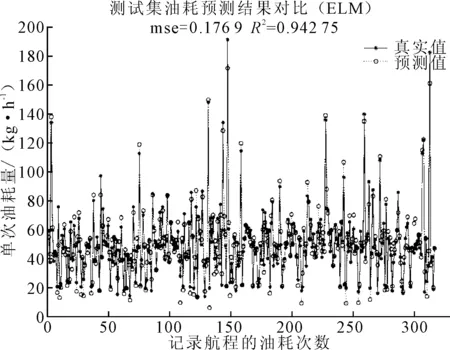
图6 ELM极限学习机测试集预测结果

将SVR模型的测试集预测结果对比BP神经网络、ELM极限学习机，结果见表4。表4表明4VR模型的预测误差最小且准确度最高。

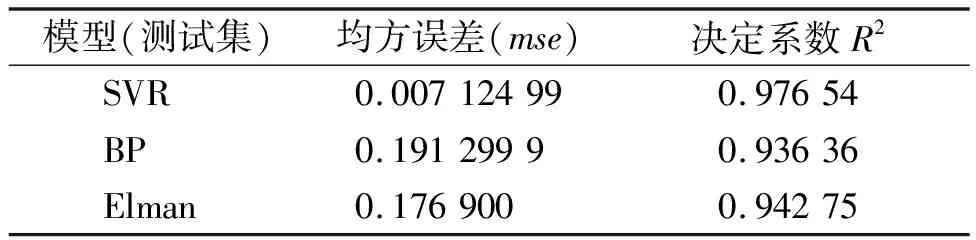
表4 SVR、BP模型和Elman测试集结果对比

4.4 模糊信息粒化SVR模型

将记录的1 320组油耗时序值作为输入数据，以每2 h为1个粒化窗口对油耗进行粒化，结果见图7。其中，Low粒子描述的是油耗2 h内变化的最小值；R粒子描述的是油耗2 h内变化的平均值；Up粒子描述的是油耗2 h内变化的最大值。

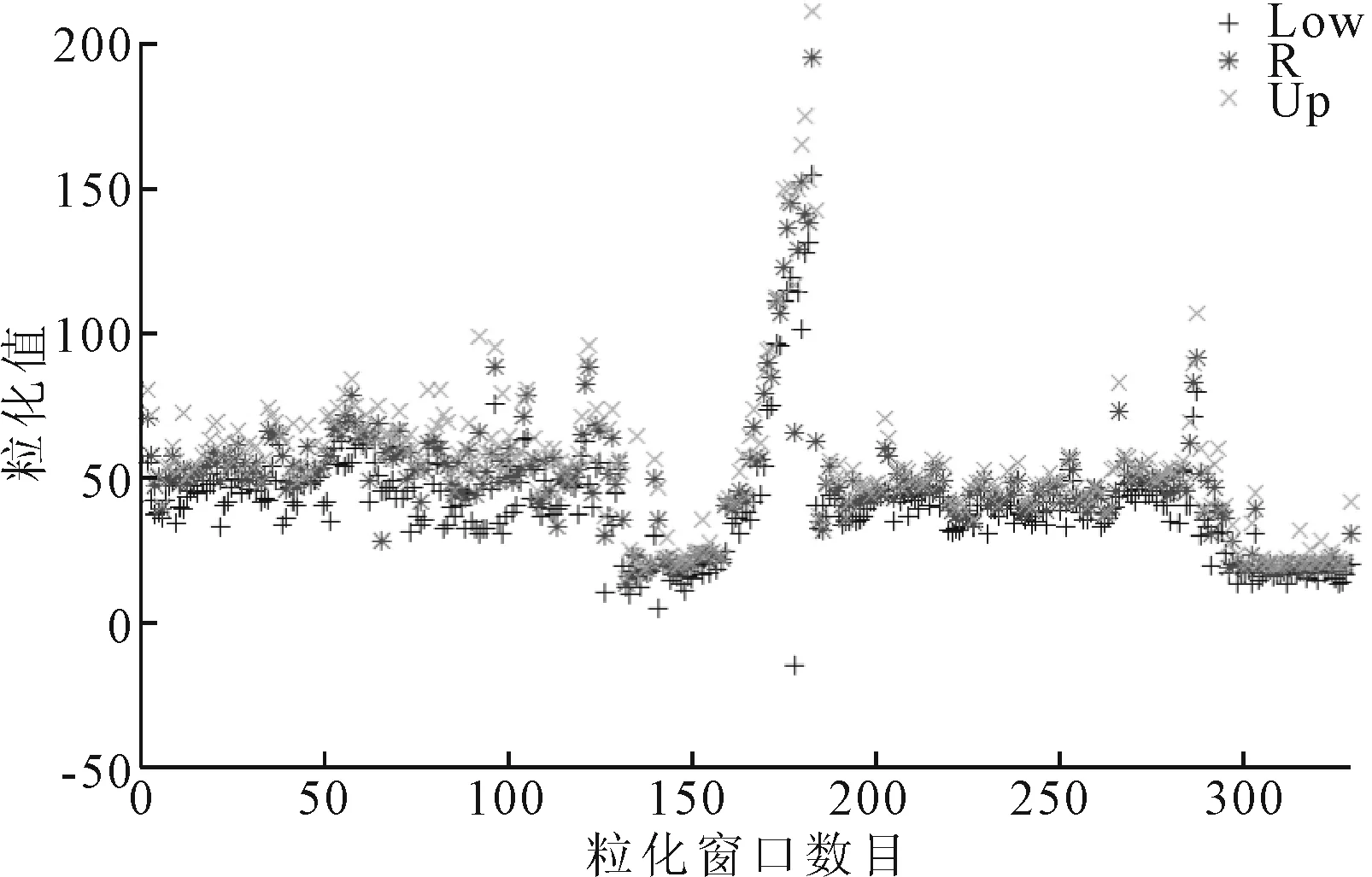
图7 模糊粒化结果

将粒化结果Low、R、Up作为SVR模型的输入参数，构建FIG_SVR组合预测模型，结果见图8。

图8表明组合模型的Low参数、Up参数预测准确率较高且符合参数走势，但R参数预测值普遍高于粒化值。这是由于目标船舶的主机分为左机、右机，航行时当只开单机(左机或者右机)时，速度低，油耗小；双机(左右机)航行时，速度高，油耗大。因此，进行预测时，对于单双机的油耗并未能区分预测，导致数据之间的跳跃性大，降低了组合模型的鲁棒性，所以平均值R参数的预测结果偏高。以Low参数为例详解FIG_SVR组合模型回归预测：选用三角型函数对油耗时序值进行FIG处理，对粒化值Low参数作归一化处理，利用交叉验证(CV)方法得到最佳参数组合C=35，g=0.125 0，根据最佳参数训练SVR模型，得到Low参数的拟合预测值，将预测值与实际值进行差值计算，误差结果见图8d)。

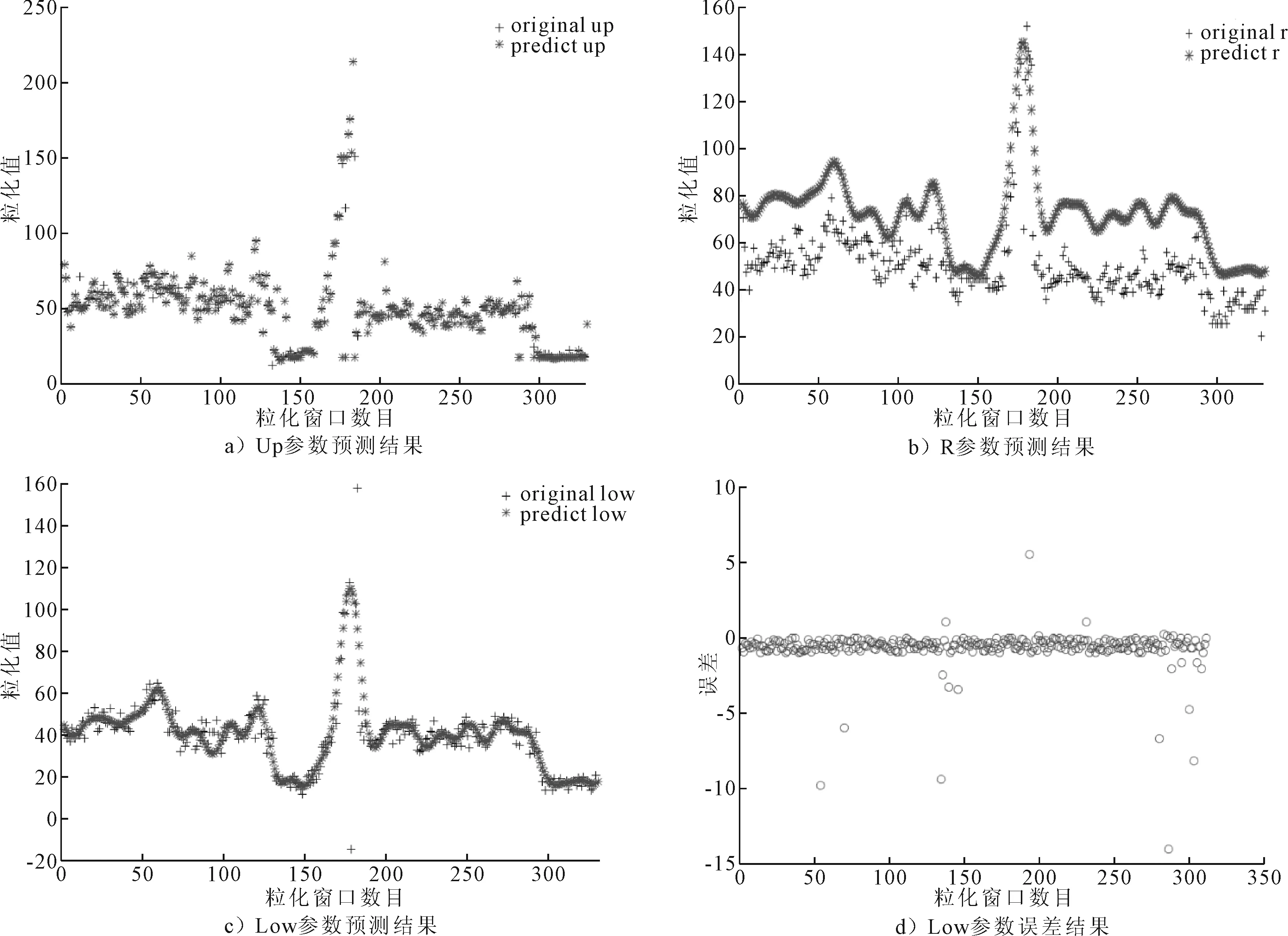
图8 粒化值Up、R和Low的SVR预测结果

4.5 油耗预测变化趋势结果验证

通过对油耗数据进行FIG_SVR组合模型的预测得到波动范围RLow、Raverage和RUp，将预测值与2 h内的实际油耗值进行比较，结果见表5。

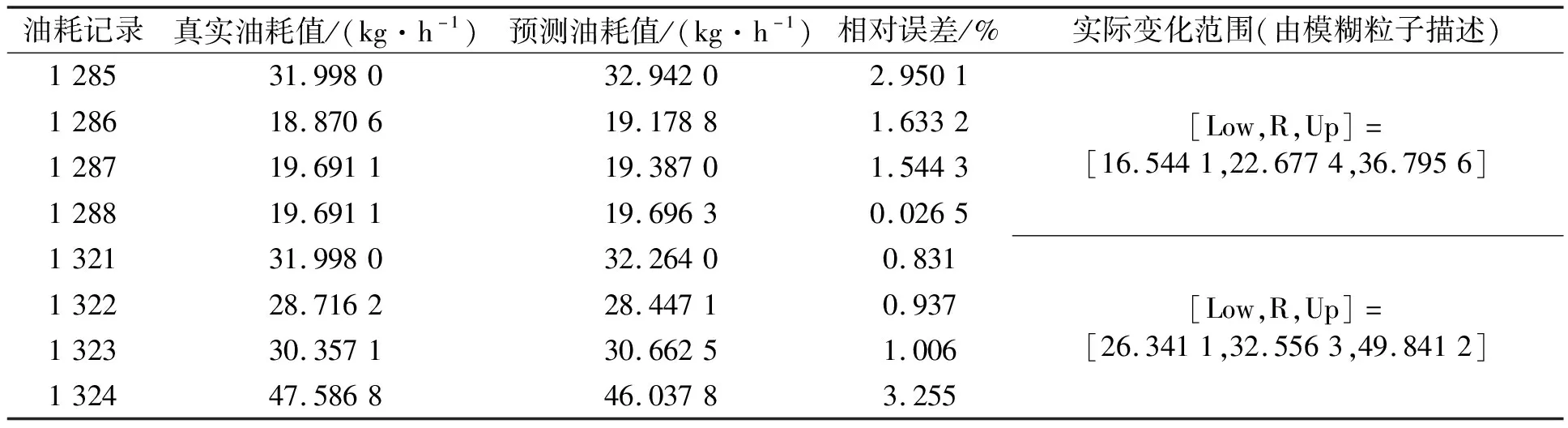
表5 船舶油耗变化趋势和变化空间预测

真实值与预测值的相对误差不超过4%，由模糊粒子提供的预测范围也符合油耗的真实波动范围。由此可见，基于模糊信息粒化的支持向量回归机组合预测模型能够准确地描述油耗未来2 h内的波动态势。

通过FIG对数据进行窗口划分和模糊化处理，以粒子为单位对油耗数据进行Low、R和Up粒子的分类。与原始数据相比，该方法对实船2 h内的油耗波动情况进行了有效的挖掘，解决了以往预测模型中大量数据模糊分类和粗糙处理的弊病；根据挖掘得到的Low、R和Up粒子通过归一化和预处理后作为输入建立泛化功能良好的SVR油耗动态预测模型，该组合模型良好的预测结果得到了合理验证。