小学生解决万以内退位减法错误类型及影响研究
2021-12-14范文贵
范文贵,李 燕
小学生解决万以内退位减法错误类型及影响研究
范文贵1,李 燕2
(1.天津师范大学 教育学部,天津 300387;2.山西省大同市实验小学,山西 大同 037000)
解决退位减法问题是运算的基础之一,国际学者非常重视退位减法问题研究.以Carla Fiori等人研究结果为基础,利用问卷调查方法对天津市4所小学455名学生进行测验.结果表明,学生解决退位减法问题包括5类错误:退位错误、使用运算法则错误、位值理解错误、混淆退位含义、其它错误;经过回归分析和相关分析发现退位错误对总失分影响最大.退位减法教学策略建议:明确跨0退位减法运算程序,多维度渗透位值制,利用图示表征退位减法算理,鼓励学生创新问题解决方法.
小学生;退位减法;错误类型;教学策略
1 问题提出
整数计算涉及到多种计算法则的综合使用.学生依据运算法则进行多位数计算时,把计算过程分解成许多步,使得每一步都只涉及一位数或者两位数的计算.整数除法、小数减法与除法都与整数减法相关,解决“万以内退位减法”既检验学生掌握两位数减法水平,又是后续整数除法、小数减法的基础.
退位减法问题研究是国际数学教育研究者关注的热点问题之一.Torbeyns等人研究结果显示:大多数学生总是依靠一种策略来解决退位减法问题,只有少数成绩较好的学生表现出解决退位减法策略的多样性和灵活性[1].四年级学生可以有效地使用间接加法策略解决退位减法.间接加法是一种有效的计算策略,间接加法可以促进学生更深刻地理解数字组成和数学问题解决过程.与大差问题(如,913-27)相比,学生更愿意使用间接加法解决小差问题(如,802-778)[2].Carla Fiori等人将学生解决退位减法出现的错误分为5类,其中带0的被减数错误率较高,“从0退位”是最容易引起学生出现计算错误的[3].国际研究成果引发对“退位减法问题研究”的深入思考.由于退位减法的复杂性,小学生并不能完全理解它的算理.学生计算错误背后隐藏着计算法则错误,学生在执行计算过程中运用错误的程序性知识.有的教师只是将学生的算术计算错误看成由学生的粗心或者不良计算习惯造成的,这是片面的认识.
学生解决万以内退位减法现状如何?研究将为教师提供小学生解决“万以内退位减法问题”出现错误类型及其原因,有助于教师更好地把握学生解决减法问题的表现,为教师开展退位减法教学以及整数除法、小数减法教学奠定基础,以确保学生有机会在数学学习上取得成功.
2 学生解决退位减法问题研究基础
2.1 关于“错误”
van Lehn对学生解决问题持续发生的程序错误进行分析,反映出学生缺乏概念知识的程序错误与偶尔发生的程序错误;一些数学事实错误是由于学生的算法不规范而导致的.这些错误反映学生从长期记忆中检索数学基础运算的困难或使用不正确计数策略[4]学生的普遍错误不同于随机错误,有些错误概念即使经教师一再提出证据讲解、提醒,仍然重复出现.有一些错误概念具有历史前导(historical precedence),意指当前学生所犯的错误,以前的学生也发生过.学生的错误概念并非是随机发生的,他们的概念发展类似于科学历史的演进.错误能够反映出学生在解决问题时的内在思维过程;换个视角来看,将错误从负面的学习失败转化为诊断学习的工具,展示错误有其教育上重要的价值[5].不同的人会有同样的错误,具有系统性,通常可以找到正确的理论加以解释.有一些错误是个体所独有的,必须观察学生回答一连串问题的反应后,理解学生思考特点.
学生的计算错误除了基本运算过程的偶然错误之外,最主要是来自于系统性的错误,而且这样的系统性错误多是在学习过程中产生.学生通常不知道他们使用了错误的计算过程,而认为他们所使用的计算过程是正确的,错误是随机出现的.学生只是将错误的运算过程固着于认知过程中,这种错误就很不容易改变,会影响以后的学习效果.
Ashlock指出:计算的错误并非是由于粗心或缺乏过程性知识所造成的,错误是由于不完全的学习和渐渐养成习惯所造成的.学生使用不同种类的错误过程,会产生更多种类的错误,因此分析学生错误的类型,探究学生犯这类错误所使用错误策略的原因,可作为改进教学的指导方向[6].Blando研究结果则显示学生一再犯同样的错误,表示其对数学基本概念的误解[7].学生错误的答案通常有一部分是正确的,它反映了学生对数学知识理解程度;找出错误的部分并且理解为什么它是错的,将会为学生的理解能力和元认知能力的发展提供强有力的帮助.
上述关于“错误”研究,确定错误的频繁性、稳定性和普遍性,阐明错误矫正的复杂性与反复性.这些结论对小学生的退位减法解题错误的分类与归因具有指导作用.对学生错误模式的定性分析,为教师提供识别学生错误类型并确定学生的误解和困难的机会.如果这些错误模式未及早纠正,则错误模式可能会持续存在,影响学生更高层次数学学习.
2.2 学生解决退位减法的错误
国际学者开展退位减法问题研究,从不同角度将错误进行分类.解决多位数的退位减法问题,当0在中间位数时会产生特别一类的退位错误类型[11].Carla Fiori 给出4个错误类型:E1(借位技术错误,忘记退位),E2(不需要借位,而出现借位),E3(基础计算错误,例如:计算20以内减法错误),E4(疏忽,或者抄错数等)[3].Raghubar将学生的错误分为5类:基础计算技能(14-8=5),竖式计算中用大数减小数(83-44=41,即个位4-3=1),忘记退位后减1(742-136=616,其中十位4-3=1,忘记从4退1,只剩下3),跨越0借位出现“0-N=N”模式(例如,106-70=176,其中十位0-7=7),其它错误(视觉监控错误:计算结果中多一个9,如图1),马虎[12].西班牙学者从“书写数字的错误、数字位置错误、运用计算法则错误、重组减法错误(忘记退位、或者总是退位)”等方面对学生解决退位减法所犯的错误进行分类[13].Watson等人研究葡萄牙小学生加减计算问题,确定减法错误类型,包括计算错误、退位错误、有关0的错误、用大数字减小数字、遗漏数字等[14].Riccomini研究发现:只有60%的教师正确地识别学生进行减法运算时出现的两类系统性错误(smaller-from-larger(SFL))和borrowing across a zero digit(BAZ)的问题[15].
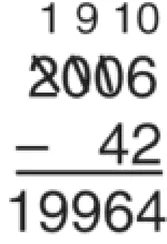
图1 视觉监控错误
学生解决退位减法可以采用以下策略:分解策略(例如,学生尝试分解两个整数的多个百位、十位和个位,并分别减去它们);顺序策略(例如,457-298=?先减去数个百,接下来减去数个十,最后由第二个整数减去第一个未分割整数);多变的策略(它涉及到学生根据对数字关系的理解或算术运算的属性灵活调整问题中的数字和操作)[16].Nemeth等人研究结果表明,在引入标准书写算法后,不管数字的特点如何,学生都主要使用它.学生灵活使用数字分解(补偿)策略解决多位数字减法问题频率偏低[17].Fischer等从答案的正确性方面分析学生使用计算方法解决退位减法问题的有效性,明确学生运算结果正确率与使用的书面计算方法密切相关.与三年级学生相比,五年级学生更多选择分解方法来解决退位减法问题[18].
综上,退位减法的相关研究受到诸多国际研究者关注.研究者基于定量和定性层面开展退位减法解题错误研究,识别错误分类,确定错误的特征.这些研究成果构成对学生解决退位减法问题的错误进行分类研究的一个基本模型,是退位减法错误类型研究的重要理论来源之一.
3 研究问题与设计
3.1 研究问题
基于以上文献分析,确定3个研究问题:(1)学生解决“万以内退位减法”的错误类型及相关分析;(2)学生解决“万以内退位减法”出现错误的原因;(3)基于错误原因分析,提出开展退位减法教学策略.
3.2 研究工具与数据分析方法
研究对象来自天津市南开区WML小学、河西区LZ小学、西青区DLT小学以及宁河区LY小学的三年级学生,每所小学随机选取测试班级,有效试卷共计455份,占总数98.6%.其中市区小学两所,郊区小学两所.
为了考查学生关于退位减法的算理和分步计算的理解能力,研究采用自编退位减法测试题.包括4个维度:
(1)被减数不含0且不含1的退位减法,共5个题;
(2)被减数含0但不含1的退位减法,共5个题(其中包括三位数减法4个题、四位数减法1个题);
(3)被减数含1但不含0的退位减法,共9个题(其中包括三位数减法6个题、四位数减法3个题);
(4)被减数既含0又含1的退位减法,共4个题(都是四位数减三位数的题).还设计3个选择题,共计26个计算题,学生用40分钟完成.
研究试卷总计90分,按位值计算得分,即个、十、百、千位得分互不干扰,计算正确一位就得一分.在测验卷中学生扣掉一分代表一种错误.最后统计每一位学生在每一题上的得分及总分,形成EXCEL数据表,并利用SPSS软件对“退位错误、运用运算法则错误、位值理解错误、混淆退位含义、其它错误”进行数据分析.
3.3 信度和效度
为了更进一步研究学生解决万以内退位减法的错误类型及不同错误类型对学生学习退位减法的影响大小,根据《义务教育数学课程标准(2011年版)》要求和人教版教材内容,确定测试内容.首先,通过整理大量文献,借鉴国际研究成果的试题结构,在综合研究的基础上编制了万以内退位减法测试卷.然后,邀请心理学专家、数学教育专家对划分测试维度和指标、组卷前测试题目与相关测试指标的适切性进行有效评估.接着,分别从测试评价和课堂教学等不同角度让教研员、小学数学教师对测试题内容、难度提出意见(例如,原题有的数字偏大,多次退位、难度大).最后,研究者对测试内容进行反复斟酌,研讨每一个试题,对测试卷进行两次修改,力求提高问卷的内容效度.信效度分析结果如表1、表2所示.

表1 信度分析结果

表2 效度分析结果
4 错误类型对总失分影响的统计分析
4.1 错误类型失分与总失分之间积差相关
基于上述相关文献分析,结合《义务教育数学课程标准(2011年版)》,综合专家、小学数学教师访谈的结果,确定学生错误分析的5个维度:退位错误、运用运算法则错误、位值理解错误、混淆退位含义、其它错误.

表3 错误类型及试卷测评指标
进一步研究5种错误类型与学生总失分之间的影响程度,利用积差相关系数分析总失分与不同错误类型的关系,结果如表4所示.

表4 测验总失分与5种错误之间相关矩阵
注:*表示<0.05,**表示<0.01
从表4中可以看出,测验卷的总失分与归类后5种错误类型以及5种错误类型之间在<0.01水平(双侧)上都呈显著正相关.其中,总失分与退位错误两者呈高度正相关(=0.849),表明学生犯退位错误越多,对总失分影响越大.退位错误与运算法则错误(=0.330)、混淆退位含义(=0.103)、其它错误(=0.375)之间呈低度相关;运算法则错误与其它错误(=0.356)、位值与占位错误(=0.111)之间呈低度相关,与总失分(=0.535)之间呈中度相关;位值与占位错误与其它错误(=0.209)之间呈低度相关,与总失分之间(=0.294)之间呈低度相关;混淆退位含义与总失分(=0.197)之间呈低度相关;其它错误与总失分(=0.761)之间呈高度相关;除此以外其它两两错误类型之间并没有显著相关性.
4.2 回归分析
回归分析不仅可以定量揭示不同错误类型失分与总失分之间的影响大小,还可以通过回归方程对总失分进行预测和控制.对5种错误类型进行数据统计的回归分析(表5).
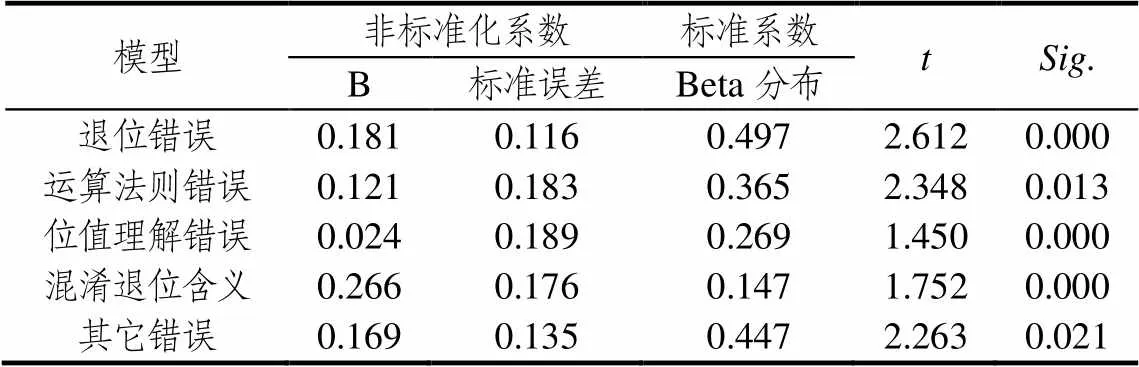
表5 回归系数
从表5的统计数据来看,退位错误、运用运算法则错误、位值理解错误、混淆退位含义、其它错误对总失分存在显著性影响.5个标准化回归系数中,退位错误的系数最大(0.497).减法计算过程中的错误主要是正确规则的缺失或者不恰当地引入了其它计算技能的规则.“退1作10”是高阶到低阶单位转换的过程,同时在运算过程中,退位数位发生的变化是非典型分割的过程.相关的退位错误又可分为多个种类,例如,越过“0”借位,即在借位遇到0时,跳过0向前一数位借;忘记退位(例如,63-57=16),也常有学生对借位的时机做出错误判断,即不该借位时却借位(详见下文有关案例).回归分析结果表明:在5种错误中,退位错误对总失分影响更大一些.研究结果进一步说明:学生的计算错误并非随机发生,不同人会犯相同错误,一些错误具有普遍性,退位错误应引起教师重视.
5 退位减法运算错例及原因分析
学生学习减法程序性知识即是获取恰当新的运算法则.学生计算退位减法出现错误的原因:正确运算法则的缺失或者不恰当地引入了其它计算技能的规则.下面结合案例,分析学生解决退位减法的5种错误的原因.
5.1 退位错误
前面量化分析中,退位错误是减法运算中错误率最高的类型.案例分析学生退位错误的原因,如图2,个位上0减9不够减,向十位借位,十位上5退位后应该减去1变为4,但学生在处理时仍然采用5-4=1,导致错误.学生在进行计算时,某一位上数值不够减,学生知道需要向前一位借位后进行计算,但存在忘记退位的现象.
学生解决运算问题涉及记取关键要素及其相互关系.学生在解题时,往往在认知负荷较大的步骤上产生较多的错误,其错误的原因并非没有掌握有关的解题规则,而是其工作记忆的容量有限的缘故[19].

图2 退位错误(1)
有证据表明退位减法运算增加了问题难度,特别是连续退位,需要学生记忆多步退位[20].受加法进位顺序影响,学生直接按照进位加的顺序标注退位点.这将引起退位混乱,有的学生忘记某数位是否退位(特别是被减数中间带0或者几百、几千).忘记退位的突出表现在解决连续退位,特别是解决被减数带0的退位减法,学生出错明显.当学生尝试从零借来并且不继续从零向左的退位时(图3,602-437=265,学生没有从百位借1),发生向零位数字借位.
认知发展不仅是掌握复杂的规则,而且必须能够抑制先前获得的一些经过熟练学习和使用的知识与技能.受到负迁移学生错误判断借位的时机,即不该借位时却借位.学生先前所接受的知识技能对即将要解决问题造成干扰,从而导致错误的现象.有的学生还出现不需要退位却退位的状况.如图4,个位上0减9不够减,向十位借1.在计算十位时,虽然十位上4减4够减,但学生仍然向百位借1.

图3 退位错误(2)
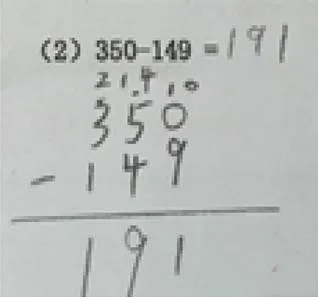
图4 退位错误(3)
如图5,在运算1 000减777时,在被减数个位0上也点了退位点,没有考虑到个位是否有退位需求或是个位退位的合理性,体现出学生见到0即想退位的思维定势.如图6,明显十位够减,但是学生还是在被减数的百位上点退位点.
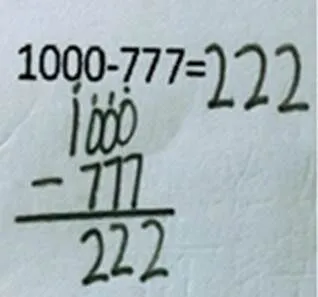
图5 退位错误(4)
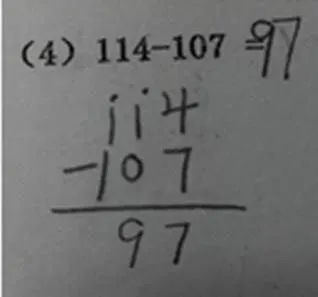
图6 退位错误(5)
当学生在学习计算、建构知识时,企图利用自己的观念去修正所学的知识,因此造成了错误的观念,并在往后的作业中一再出现相同的错误类型.有的学生出现“退位两次”的错误,特别是连续退位减法中,对某一数位上连续退位两次,即计算时将本位上的数字减去2进行计算.例如图7,学生运算400减165时给出他的自然的错误解法:“我先列竖式,相同数位对齐,从个位开始减,个位上是0,0减5不够减,向十位借,十位上是0,借不到,所以向百位借,并在4上面点上个点,借1当10,10减5等于5;再算十位,十位上也是0,0减6不够减,所以再向百位的4借1当10,再点上一个点,十位的10减6等于4;再算百位,百位上的4借了两次,所以还剩下2,2减1等于1.所以,400-165=145.”
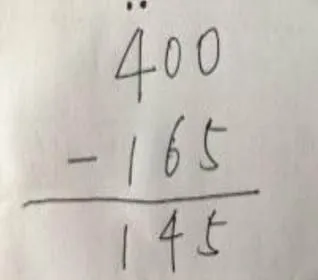
图7 退位错误(6)
5.2 使用运算法则错误
在解题过程中,学生遇到困难,不会立即放弃,会寻求其它法则来解决问题,若是在寻求其它解决方法中有误,则整个解答过程便会产生错误.作减法时,有的学生虽然明白不够减需要退位,但在实际的运算中,却采用的是加法的运算法则,在同一个减法计算中,学生一会采用减法,一会采用加法计算,导致运算出现错误.图8中,个位数字是3减7不够减,学生明白需要向前一位借1,但在实际中却直接将大数7减去小数3,将所得结果4写在差的位置.
有的学生依据自己先前学习的知识建构出不适当或错误的运算规则.他们学习新的数学知识时,对正确的运算规则做出过度类比或臆想,误用旧经验解决新问题,新的知识与旧经验相互干扰产生错误.当学生不了解教师所教授的知识和书本的说明时,学生会企图利用自己的观念去改变所学的知识,因而造成错误.有的学生在计算时,将退位后所得10直接减去减数上所对应数位,将所得结果写在差相应数位上,而不加上被减数中原位置上数字,出现程序错误.图9中,十位上退位后为2,2减4不够减,向百位借1,学生将百位退1后得到的10直接减去4,而没有加上十位上数字2,而出现错误.

图8 退位错误(7)
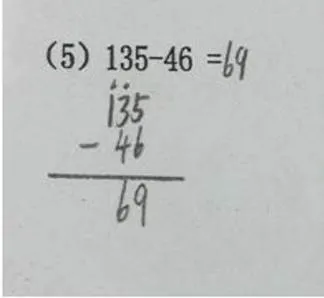
图9 退位错误(8)
5.3 位值理解错误
5.3.1 位值含义理解错误
由于数学程序知识与概念知识之间的密切关系,学生的程序错误反映出学生缺乏十进制位置概念系统知识.David M M研究表明:学生解决退位减法最频繁出现的错误模式来自于缺乏对位值制数字系统的意义理解[12].对于被减数的数字经过借位或数字重组后,有的学生认为数字在借位前和借位后,被减数的数值会改变.
在学习历程中,概念的混淆常常是来自记忆中学习经验的相互干扰.需要退“1”作十解决退位减法问题时,一些学生不能将十进制与竖式减法联系起来[21].如图10,学生在表示十位的方框中写10,则被减数就变成“53 101”不是原来的四位数,因改变竖式计算中位值本身的含义而出现错误.学生使用自己的方法解决问题并且感到满意,而不管题目的原义,只要能求出他认为对的答案就可以了.
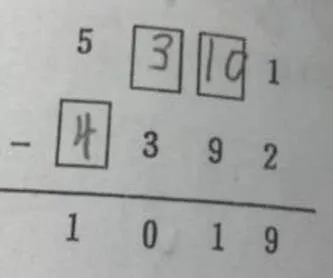
图10 退位错误(9)
5.3.2 首位误用0占位
学生误用记数规则.如图11、图12,在测验中,有的学生忘记记数规则,在计算时遇到首位上得数为0时,首位上仍然写0占位.
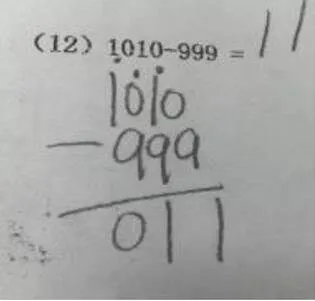
图11 退位错误(10)

图12 退位错误(11)
5.4 混淆退位含义
在不连续退位情况下,减法退位顺序与加法进位顺序相似,左侧数退“1”,退到右侧数位形成退“1”作十,与右侧数位上的数组合(这是数字等价变换),但是有的学生存在理解错误.
5.4.1 混淆1退位后含义
当被减数中含有1的减法在向1退位时,有的学生将1看作10,1退位后变成9,当计算1所在数位时按照退位后所得9来进行计算.如在图13中,个位上4减7不够减,向十位借1,退位后个位变成14减7得7;十位上学生将1退位后当作9,9减3得6,出现错误.
5.4.2 混淆0退位后含义
针对“从0退位的错误”的类型,以往研究中有多位数的退位问题,当0在中间位数时会产生特殊的退位错误类型.如图14,被减数中含有两个0,十位上“1”点上一个退位点后,个位“0”的含义变为10,10减9得1,第二个“0”在百位,由于已经退过位,此时百位“0”上点退位点的含义为9,而学生仍然将此“0”当作10来计算而出错.
5.5 其它错误

图13 退位错误(12)
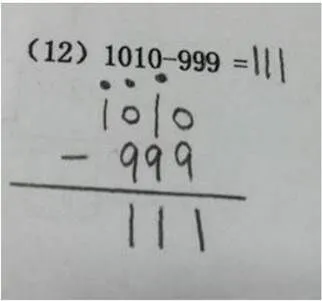
图14 退位错误(13)
在退位减法计算中,学生已经掌握基本算理,运算过程也正确,但由于粗心出现的个别错误,如:抄错题、遗漏数字、马虎、空题等错误,由于这些因素并不是学生在退位减法中加强算理等认知因素所引起的,在测验中将此类错误归为其它错误.
6 基于退位减法错误研究开展教学
6.1 明确跨0退位减法运算程序
教师不仅识别出学生解决问题中出现的特殊类型错误,他们能根据这些错误的特点提供有针对性的指导.为了矫正学生解决退位减法出现的从0退位的错误(图2;文[3]、文[11]等),基于减法的原始竖式形式,学生要理解退位原理.
古代中国人用算筹进行计算,有一套方便方法.筹算加减法很简单,“由高位算起”(图15,即由左向右计算)[22].
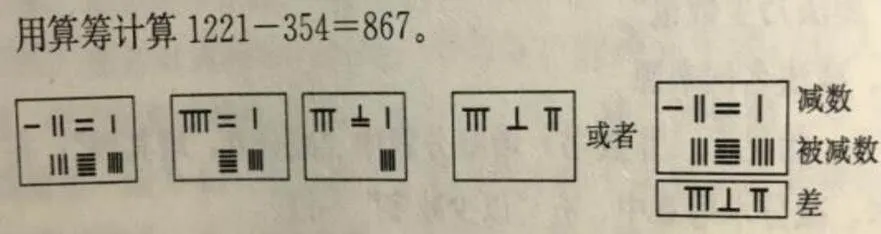
图15 算筹计算案例
虽然现在计算都是从低位算起,但是在连续退位情况下,减法退位顺序与加法进位顺序相反,特别是被减数中间带0或者被减数是几百、几千,需要在非0的高位点退位点(退“1”),再按数位向右依次退“1”作十.如图16,在进行计算500减403时,学生发现个位是0不够减,结合以前学习经验,学生会让十位退“1”;而十位同样为0,无法退“1”;学生要想到继续向前,让百位退“1”.即学生明确跨0的退位减法程序:首先从非0的高位退“1”,再完成后续各个数位退“1”作十,直至个位减法.
6.2 多维度渗透位值制
教师将位值概念转化成有利学生理解数字的方式.学生能察觉到退位减法的方向性、被减数与减数不可互换;自左邻位值退“1”作十到靠右的该位值,并了解退位使得该位值数量变大、使整个多位数数量变小;任一位值的数字相减时,如同个位数相减.退位也就是在高阶单位和低阶单位之间做转换,总之不会因为重新命名而改变.
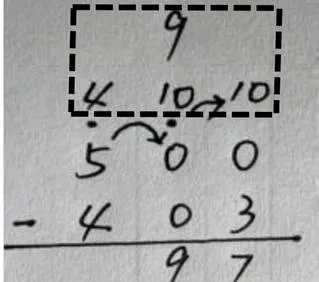
图16 跨0退位减法案例
减法运算的过程与位值概念的发展是密不可分的.学生对位值的理解,影响学生在进行减法运算时所使用的策略.让学生明白不同位值所代表的含义,在遵循减法运算基本规则下,引发学生认知冲突;利用教具或者课件向学生呈现“退位”后各个数位上数值的变化,学生理解根据不同数位上数值,再进行减法运算.
教师要了解位值概念的发展模式,掌握各成分知识的难易排序,依据由易至难顺序:位置知识、群组知识、数字对应、分割知识.学生不仅了解满10进“1”和退“1”作10、知道10个“1”等于1个“10”,以及“相邻单位呈十倍关系”,还要能够将数依典型分割或非典型分割方式表示,同时也能依据数字所在位置辨识其数值.
6.3 利用图示表征退位减法算理
学生没有掌握算理,很可能还是不会解决问题,甚至重复地出现相似或者相同的错误,即使大量重复训练,也会导致其数学问题解决能力发展故步自封、停滞不前[23].学生从具体表征阶段需经历“半具体、半抽象”阶段才到达“抽象”阶段,学生将知识内化,逐渐将表征抽象化,将真实世界与数学抽象世界联系起来.针对退位的步骤,教师访谈学生“被减数退位后数值的变化情况?”发现多数学生只是熟记运算法则,对于退位的深层意义根本不了解,也不知道退位的动作并不会使被减数的数量减少.
Thanheiser利用正方形、条形图、点子图等图形给出解释数字重新组合,说明重新组合后数字的值保持不变[24].从具体、半具体到抽象,让学生画出符合题意的图示表征以协助学生理解题意.例如,403-158=?学生理解算法背后的算理吗?明确点“两个退位点”顺序吗?通过画图,学生解释算理(如图17):画4个大圆表示400,画3个小棒表示3,3-8不够减,而十位是0,无法退位,进而让百位退“1”.百位上4退“1”(1个百)后圈出一个圆,这一个圆(表示1个百)到达十位后变成10个小圆(每个小圆表示1个十).继续向个位退“1”,十位圈出一个小圆到个位,变成10个小棒,加上原来的3根小棒,此时个位上数字为“13”.个位上13-8=5,十位上剩余9,9-5=4,百位上剩余3-1=2,得数245.
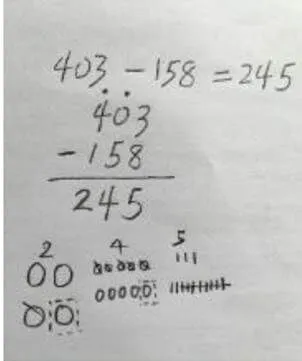
图17 退位计算算理
学生的计算能力建立在数列、数物、基数等能力完备发展的基础上,这些先备知识对于学生以后数学学习成效影响深远.在课堂教学中,在遇到难点时,教师指导一些学生借助画图的方式辅助思考算理.从文字表征转译为图像表征的转译活动,将问题复杂且抽象的关系,透过画图表征让学生了解题目的特征,使一些难以理解的数量关系变得具体化且有可诠释性,促进学生发现隐藏在条件间的关系.
6.4 鼓励学生创新问题解决方法
《计算之书》描述的整数四则运算规则与现在的计算规则基本相同,但“退位”方法与现今不同,现在的规则是把被减数下一位减去“退位数”,而斐波那契却把减数下一位加上“退位数”.例如图18,如要从380中减去92,把92写在380的下面,因为从0中减去2是不可能的,将0加上10,得10,减去较小数中的2,得8,把它放在第一位,因为增加10,故把1保留在手中,把它加上9,得10,从8中减去10,但是这是不可能的;把它从18中减去,得8,放在第二位,保留1并从3中减去;得2,放在第三位,因此得到288就是减法的差[25].
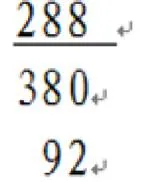
图18 斐波那契的退位方法
Carpenter T P等人的研究结果表明,孩子们可以发明加法和减法的策略,大约90%的学生使用自己发明的问题解决策略.在学习标准算法之前,使用发明策略的学生更好理解十进制概念.与最初学习标准算法的学生相比,他们会更成功地将他们发明的问题解决策略应用到新的情境[26].Carroll和Porter研究发现,有的学生自己发明退位减法的解决问题策略,当减数较大时,不需要“退位”或重组,而是用负数,例如,62-25=40+(-3)=37[27].
Thanheiser从“数的组成与分解、退1等10”两个角度探究学生计算“735-264=471”的方法[28].学生学会灵活解决问题.这些策略涉及到根据对数字关系的理解或算术运算的属性灵活调整问题中的数字和操作.变化策略的一个例子是补偿策略,例如,601-234=(600-234)+1=366+1=367;457-298=457-(300-2)=157+2=159.
7 研究结论与讨论
研究提供了小学生解决多位数退位减法中所犯的错误类型的系统分析.基于国际视野,把握退位减法的前沿研究成果,收集问卷测试数据,经过相关分析和回归分析,发现5类错误与总失分之间关系.特别是,退位错误对总失分影响最大.在案例分析研究中,发现学生难以理解0的含义以及将其作为数字来解决退位减法问题.教师应关注学生解决问题的高概率错误.这项研究帮助教师在处理减法时参与选择练习,使他们意识到选择所用计算方法的重要性.解决减法问题使学生对数学产生恐惧并对其掌握数学概念的能力失去信心[29].基于理解视角,学习数学需要教师具有识别学生错误类型的能力,这些错误反映了学生对概念缺乏深刻地理解.开展退位减法的错误分析为教师提供有关学生思维、理解和误解的重要信息.理解位值制对于提升学生多位数加法、减法计算技能至关重要.诊断评估学生错误模式有利于教师尽早为学生提供有意义矫正错误的机会,促进学生获得数学成功的机会.
研究只以天津455名学生作为调查对象,存在地区局限性,未来可继续探索全国多区域小学生解决退位减法的现状;探索小学生解决整数退位减法与小数减法之间的关系.
[1] Torbeyns J, Hickendorff M, Verschaffel L. The use of number-based versus digit-based strategies on multi-digit subtractions: 9-12-year-olds’ strategy use profiles and task performances [J]. Learning and Individual Differences, 2017 (58): 64–74.
[2] Hickendorff M. Fourth graders’ adaptive strategy use in solving multi-digit subtraction problems [J]. Learning and Instruction, 2020 (67): 1-10.
[3] Fiori C, Zuccheri L. An experimental research on error patterns in written subtraction [J]. Educational Studies in Mathematics, 2005 (60): 323–331.
[4] Vanlehn K. Bugs are not enough: Empirical studies of bugs, impasses and repairs in procedural skills [J]. The Journal of Mathematical Behavior, 1982 (3): 3-71.
[5] Borasi, Raffaella. Capitalizing on errors as “springboards for inquiry”: A teaching experiment [J]. Journal for Research in Mathematics Education, 1994, 2 (25): 208.
[6] Ashlock R. Errors patterns in computation: Using error patterns to help each student learn [M]. 10th ed. Boston: MA, 2010: 36.
[7] Blando J A, Kelly A E, Schneuder B R, et al. Analyzing and modeling arithmetic errors [J]. Journal for Research in Mathematics Education, 1989, 20 (3): 301-308.
[8] Selter C, Prediger S, Marcus Nührenbörger, et al. Taking away and determining the difference: A longitudinal perspective on two models of subtraction and the inverse relation to addition [J]. Educational Studies in Mathematics, 2012 (79): 389-408.
[9] Selter C. Addition and subtraction of three-digit numbers: German elementary children’s success, methods and strategies [J]. Educational Studies in Mathematics, 2001 (47): 145-173.
[10] Csaba C. Strategies and performance in elementary students’ three-digit mental addition [J]. Educational Studies in Mathematics, 2016 (91): 123–139.
[11] Carpenter T P, Franke M L, Jacobs V R, et al. A longitudinal study of invention and understanding in children’s multi-digit addition and subtraction [J]. Journal for Research in Mathematics Education, 1997, 29 (1): 3-20.
[12] Raghubar K, Cirino P, Barnes M, et al. Errors in multi-digit arithmetic and behavioral inattention in children with math difficulties [J]. Journal of Learning Disabilities, 2009, 42 (4): 356-371.
[13] Margalef-Ciurana m, García-Tamarit C. The application of a digital educational resource to the learning disability of subtraction: A case study [J]. Contexto Internacional, 2016, 33 (1): 71-102.
[14] Watson S, Lopes J, Oliveira C, et al. Error patterns in Portuguese students’ addition and subtraction calculation tasks: Implications for teaching [J]. Journal for Multicultural Education, 2018, 12 (1): 67-82.
[15] Riccomini P J. Identification and remediation of systematic error patterns in subtraction [J]. Learning Disability Quarterly, 2005, 28 (3): 233-242.
[16] Torbeyns J. Mental computation or standard algorithm? Children’s strategy choices on multi-digit subtractions [J]. European Journal of Psychology of Education, 2016, 31 (2): 1-18.
[17] Nemeth L, Werker K, Arend J, et al. Corrigendum: Interleaved learning in elementary school mathematics: Effects on the flexible and adaptive use of subtraction strategies [J]. Frontiers in Psychology, 2019 (86): 1-21.
[18] FISCHER J P, Vilette B, Joffredo-Lebrun S, et al. Should we continue to teach standard written algorithms for the arithmetical operations? The example of subtraction [J]. Educational Studies in Mathematics, 2019 (101): 105-121.
[19] Ayres, PAUL L. Systematic mathematical errors and cognitive load [J]. Contemporary Educational Psychology, 2001 (26): 227-248.
[20] Imbo I, Vandierendonck A, Vergauwe E. The role of working memory in carrying and borrowing [J]. Psychological Research, 2007 (71): 467–483.
[21] Thanheiser E. Understanding multi-digit whole numbers: The role of knowledge components connections, and context in understanding regrouping 3+- digit numbers [J]. The Journal of Mathematical Behavior, 2012, 31 (2): 220-234.
[22] 徐品方,张红,宁锐.中学数学简史[M].北京:科学出版社,2007:19.
[23] Watson I. Investigating errors of beginning mathematicians [J]. Educational Studies in Mathematics, 1980, 11 (3): 319-329.
[24] Thanheiser, EVA. Preservice elementary school teachers’ conceptions of multi-digit whole numbers [J]. Journal for Research in Mathematics Education, 2009, 40 (3): 251-281.
[25] 斐波那契.计算之书[M].西硌尔英,纪志刚,汪晓勤,等译.北京:科学出版社,2007:25.
[26] Carpenter T P, Franke M L, Jacobs V R, et al. A longitudinal study of invention and understanding in children’s multi-digit addition and subtraction [J]. Journal for Research in Mathematics Education, 1997, 29 (1): 3-20.
[27] Ji-Won S. Moving beyond a traditional algorithm in whole number subtraction: Preservice teachers’ responses to a student’s invented strategy [J]. Educational Studies in Mathematics, 2016 (93): 105–129.
[28] Thanheiser E. The effects of preservice elementary school teachers’ accurate self-assessments in the context of whole number [J]. Journal for Research in Mathematics Education, 2018, 49 (1): 39-55.
[29] OLTEANU C, OLTEANU L. Improvement of effective communication—The case of subtraction [J]. International Journal of Science and Mathematics Education, 2011, 10 (4): 1-24.
Study of the Error Patterns and Influences of Primary School Students in Performing Subtractions with Regrouping for Numbers Less Than Ten Thousand
FAN Wen-gui1, LI Yan2
(1. Faculty of Education, Tianjin Normal University, Tianjin 300387, China;2. Experimental Primary School, Shanxi Datong 037000, China)
Solving subtraction problems with regrouping is one of the foundations of mathematical operations. International scholars attach great importance to the study of subtraction with regrouping. Based on the results of Carla Fiori et al., 455 students were tested using a questionnaire survey. The findings demonstrated that students solved subtraction problems with regrouping with five patterns of errors: regrouping errors, algorithm errors, misunderstanding place value, confusing the meaning of regrouping, and other errors. After regression and related analyses, it was found that the regrouping error had the greatest impact on the total loss. Based on an analysis of the cause of the error, the following teaching strategies for subtraction with regrouping are proposed: clearing the operation procedure of cross-zero subtraction with regrouping, penetrating the place-value system with multiple dimensions, graphically representing the arithmetic of subtraction with regrouping, and encouraging students to innovate problem-solving methods.
elementary school students; the subtractions with regrouping; error pattern; teaching strategy
G622.4
A
1004–9894(2021)06–0032–07
范文贵,李燕.小学生解决万以内退位减法错误类型及影响研究[J].数学教育学报,2021,30(6):32-38.
2021–07–02
天津市哲学社会科学规划资助项目——学校教育共同体精准帮扶系统构建与实效研究(TJJX18-014)
范文贵(1965—),男,辽宁锦州人,教授,博士,硕士生导师,主要从事教师教育、小学数学教育研究.
[责任编校:陈隽、陈汉君]
