2020年新高考与传统高考的比较研究——基于高考试题综合难度模型

刘 静，周思波，吴中林

2020年新高考与传统高考的比较研究——基于高考试题综合难度模型

刘 静1，周思波2，吴中林3

（1．西南石油大学 基础教学部，四川 南充 637001；2．四川师范大学 数学科学学院，四川 成都 610066；3．四川省教育科学研究院，四川 成都 610066）

2020年是新课标发布后新高考卷启用的第一年，有必要对数学学科新高考与传统高考的试题难度进行比较分析．借助武小鹏、孔企平多次改进后形成的高考试题综合难度模型，从背景因素、是否含参、运算水平、推理能力、知识含量、思维方向、认知水平7个难度因素对2020年全国数学高考共13套试卷进行编码分析．结果表明新高考试题在背景因素、推理能力、知识含量、认知水平上的要求有所变化，新高考更加注重试题情境设置的创新性和知识运用的综合性．

数学高考；综合难度；比较研究

1 问题提出

2013年，教育部启动了普通高中课程修订工作，深入总结了21世纪以来中国高中课改的宝贵经验，于2018年印发了《普通高中数学课程标准（2017年版）》，指导新一轮课程改革的实践．为回答高考内容将如何深化改革的问题，教育部考试中心于2020年1月研制发行了《中国高考评价体系》和《中国高考评价体系说明》，奠定了中国新高考改革的理论基础，文件指出高考体系由“一核四层四翼”组成，其中“一核”是指高考的核心功能，即“立德树人、服务选才、引导教学”；“四层”是指高考的考查内容，即“核心价值、学科素养、关键能力、必备知识”；“四翼”是高考的考查要求，包括基础性、综合性、应用性、创新性[1]．教育部考试中心指出新数学高考坚持改革创新，全面贯彻高考评价体系的要求，更新评价理念，落实立德树人根本任务，并在考试内容改革、题型创新、试卷结构改革以及科学调控难度等方面进行了积极探索[2]．

2021年将有8个省实行高考综合改革，使用新高考卷．在此背景下，有必要探究新数学高考卷与传统高考数学试题的考查侧重点的变化以及综合难度差异．但从试卷的表面特征判断难度变化只能得到浅表的结论，想要了解本质变化需要借助科学的工具．武小鹏对鲍建生的习题难度模型进行了改编，在原有的背景、知识点数量、运算水平、推理、认知水平5维度模型上增加了思维方向、是否含参两个维度，形成高考试题难度的评价模型，使之更符合标准化考试的评价，并用该模型对中韩高考试题进行了比较[3]．李保臻、张玉环等人分别借助武小鹏高考试题综合难度模型对不同国家与地区的高考试题进行了分析[4–5]．

2 研究对象与研究工具

2.1 研究对象

2020年高考由教育部考试中心命制了8套数学试卷，包括全国Ⅰ、Ⅱ、Ⅲ卷文理科分卷，以及不分文理科供山东使用的新高考Ⅰ卷、供海南使用的新高考Ⅱ卷．另有北京、天津、上海、浙江、江苏5个地区的自主命题卷．为了体现研究的整体性和系统性，选取以上共13套全国高考试卷作为研究对象．

2.2 研究工具

主要参考武小鹏在鲍建生难度模型基础上改进的高考试题综合难度模型．模型共提出了7个难度因素：背景因素、是否含参、运算水平、推理能力、知识含量、思维方向、认知水平．各因素的水平划分见表1．

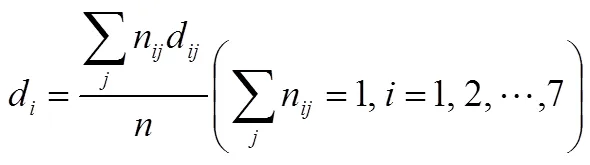
2.3 编码方法

按照表1中各难度因素不同水平的内涵描述，对2020年所有数学高考卷进行编码，编码示例如下．

例1 （全国高考Ⅰ卷文理科第3题）

埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该正四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上高与地面正方形的边长的比值为（）

该题编码为生活背景A2、无参数B1（题目涉及的计算都是静态的数值运算，没有涉及到数值的变化）、简单符号运算C3（需要设出未知边长并解方程，涉及到对于符号的加、减、乘、除、开方等运算）、D1简单推理（推理只需要1步：根据提示和示意图列出各边长之间的等量关系，化简计算即可得出结果）、单个知识点E1（立体几何的结构特征）、顺向思维F1（按照现有的知识安排顺序，顺向直接解决问题）、运用水平G2（在立体几何基本特征的基础上通过不同生活情景做了构造，属于知识的运用）．

表1 基于高考试题的综合难度模型结构与内涵

例2 （新高考Ⅰ卷第9题）

对13套数学高考试题编码后的原始数据代入难度系数计算公式，计算出分维度难度系数及综合难度系数并整理得到表2．

表2 2020年数学高考试卷难度系数汇总

3 研究过程与结果

下面分别对13套试卷在背景因素、是否含参、运算水平、推理能力、知识含量、思维方向、认知水平各水平上的分布绘制堆积柱形图，以便于更直观地比较各套试卷在各分维度上不同水平的情况．

3.1 背景因素

关于13套试卷背景因素的统计图对比如图1所示，新高考有32%的题目是具有丰富背景的，而传统高考试卷具有生活背景或者科学性背景的题量仅占整卷的0%～22%．其中5套自主命题试卷的背景大都是纯数学背景，浙江卷更是只有纯数学背景．由表2知，13套试卷在背景因素上的难度由难到易排序为：新高考Ⅰ卷=新高考Ⅱ卷＞全国Ⅱ理科卷＞北京卷＞全国Ⅰ理科卷=全国Ⅰ文科卷=全国Ⅱ文科卷=全国Ⅲ理科卷=全国Ⅲ文科卷＞江苏卷＞上海卷=天津卷＞浙江卷．

3.2 是否含参

图2展示了13套试卷题目中是否含参的情况．含参题量最多的是全国Ⅰ理科卷、全国Ⅱ理科卷和上海卷，也仅有这3套试卷的含参题量高于50%，含参题量最少的是全国Ⅱ卷文科，新高考卷的含参题量处于中等水平，其余试卷含参与否没有太大的区别，普遍表现为无参数略多于有参数的题目．由表2知，13套试卷在是否含参维度上的难度由难到易排序为：全国Ⅰ理科卷=全国Ⅱ理科卷=上海卷＞江苏卷=全国Ⅲ理科卷＞全国Ⅰ文科卷=全国Ⅲ文科卷=北京卷＞新高考Ⅰ卷=新高考Ⅱ卷=天津卷=浙江卷＞全国Ⅱ文科卷．

图2 是否含参因素的柱形对比

3.3 运算水平

可见数学高考试题计算水平大多集中在简单符号运算，简单数值计算次之．由表2知，13套试卷在运算水平上的难度由难到易排序为：全国Ⅰ理科卷＞新高考Ⅰ卷=新高考Ⅱ卷＞全国Ⅱ理科卷＞江苏卷＞全国Ⅲ理科卷＞天津卷＞浙江卷＞全国Ⅲ文科卷=北京卷＞全国Ⅱ文科卷＞上海卷＞全国Ⅰ文科卷．

图3 运算水平因素的柱形对比

3.4 推理能力

由图4可以看出，大部分试卷的简单推理题目多于复杂推理题目，而上海卷、浙江卷、江苏卷和新高考Ⅰ、Ⅱ卷在两部分的题量分布相当，其中新高考Ⅰ卷是唯一复杂推理多于简单推理的试卷，新高考Ⅱ卷的复杂推理占比也较高．由此可知新高考卷对推理能力的要求总体上有明确的增加．由表2知，13套试卷在推理水平上的难度由难到易排序为：新高考Ⅰ卷＞新高考Ⅱ卷＞江苏卷＞浙江卷＞上海卷＞全国Ⅰ文科卷=全国Ⅱ理科卷=全国Ⅲ文科卷=全国Ⅲ理科卷＞全国Ⅰ理科卷=天津卷＞北京卷＞全国Ⅱ文科卷．

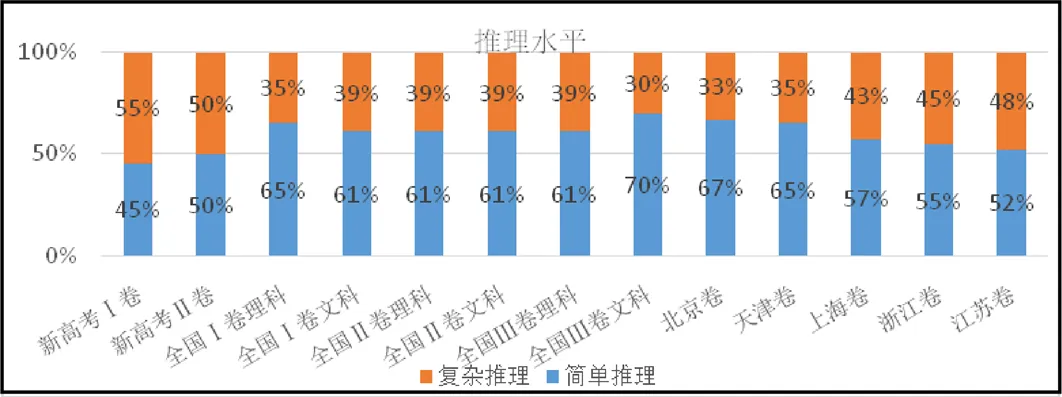
图4 推理能力因素的柱形对比

3.5 知识含量

图5展示了13套试卷题目所考知识点数量的情况，新高考Ⅰ、Ⅱ卷对3个及以上知识点的综合考查最多达到了整卷的23%，对单个知识点进行考查的题量降低为32%，对两个知识点进行综合考查的题目数量居中．上海卷、浙江卷卷考查单个知识点的题量较多，达到了50%以上，对两个知识点进行综合考查的题量最少．由表2可知13套试卷在知识点含量上由难到易排序为：新高考Ⅰ卷=新高考Ⅱ卷＞全国Ⅱ理科卷＞全国Ⅲ理科卷＞江苏卷＞天津卷＞全国Ⅰ理科卷＞上海卷＞全国Ⅱ文科卷＞浙江卷＞北京卷＞全国Ⅰ文科卷=全国Ⅲ文科卷．

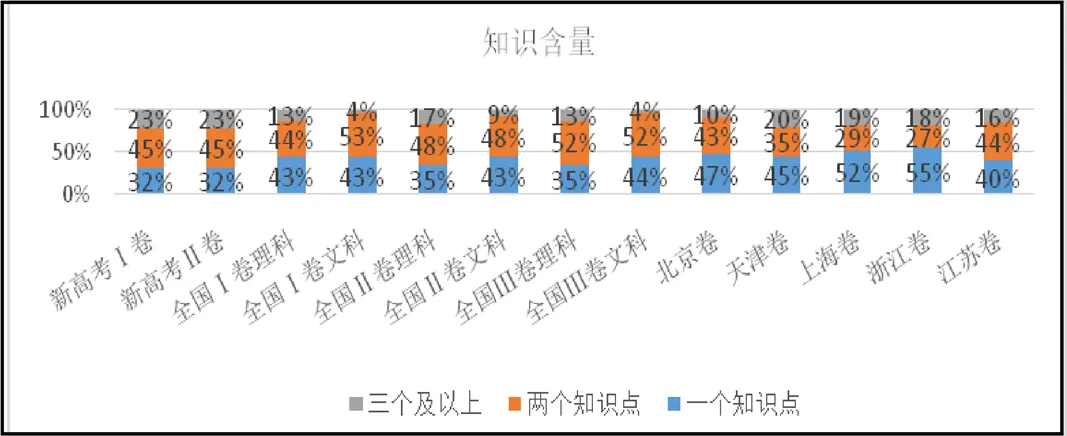
图5 知识含量因素的柱形对比

3.6 思维方向

由图6可知新高考相对传统高考的又一明显差别来自于思维方向．传统高考更重视顺向思维，而新高考更重视逆向思维的考查，新高考Ⅰ、Ⅱ卷对逆向思维的考查最多，占全卷的50%，紧接着是全国Ⅰ卷理科、全国Ⅲ卷理科和浙江卷．全国Ⅱ卷文科对逆向思维的考查最少，余下的试卷在两个思维方向上的侧重情况相近．由表2知，13套试卷在思维方向上由难到易排序为：新高考Ⅰ卷=新高考Ⅱ卷＞全国Ⅰ理科卷=全国Ⅲ理科卷＞浙江卷＞天津卷=全国Ⅰ文科卷=全国Ⅲ文科卷＞北京卷=上海卷＞江苏卷＞全国Ⅱ理科卷＞全国Ⅱ文科卷．

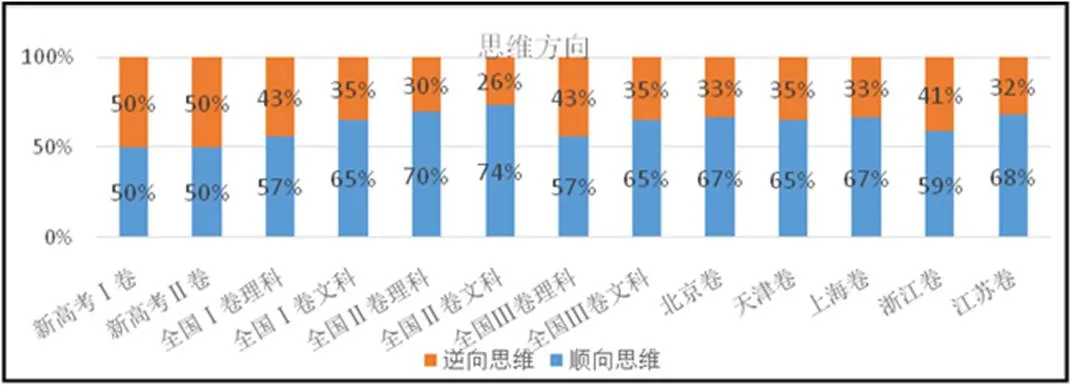
图6 思维方向因素的柱形对比

3.7 认知水平

由图7可知，13套全国数学高考卷在认知水平上的侧重差别不大，其中新高考Ⅰ、Ⅱ卷题目明显对理解层次的考查较少，仅有27%；对运用层次的考查更多，分别为46%、50%；对分析水平的考查居中．由表2知，13套试卷在认知水平上的难度由难到易排序为：新高考Ⅰ卷＞新高考Ⅱ卷=浙江卷＞上海卷＞天津卷＞江苏卷＞全国Ⅰ理科卷=全国Ⅰ文科卷=全国Ⅱ理科卷=全国Ⅱ文科卷＞北京卷＞全国Ⅲ理科卷＞全国Ⅲ文科卷．

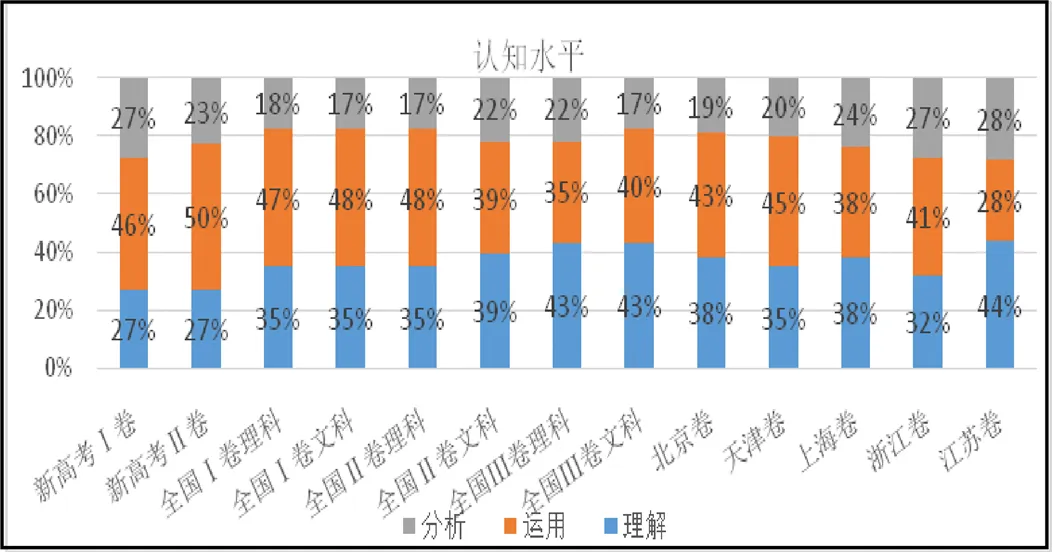
图7 认知水平因素的柱形对比

3.8 综合难度

为了更直观看到所有试卷在7个维度上的侧重程度，将各维度的难度系数作为轴标签数据，绘制了雷达图，如图8．

图8 13套试卷综合难度系数雷达图

可见新高考卷在背景因素、推理水平、知识含量、思维方向、认知水平5个维度上的难度都处于前列，这与新一轮高考改革重视对数学核心素养的考查有关．《普通高中数学课程标准（2017年版）》强调数学核心素养的培养离不开对实际问题的解决，这与学生对知识的综合运用能力、具有较高的认知水平紧密相连．而推理的复杂程度、知识点的综合运用以及现实情境的呈现都在一定程度上影响着试卷的难度．

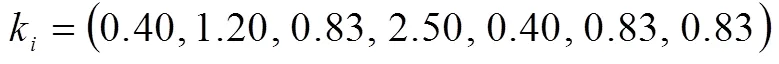
图9 13套试卷难度构成偏向雷达图

图9在一定程度上反映了13套试卷的难度构成偏向．总的来说，13套试卷在7个维度上的考评侧重是一致的，都重视对推理能力的考查，而且对该维度的考查力度远大于其他维度，其次是对知识的认知水平和运算能力．因而教师在教学中应当重视对学生相应能力的培养．

4 研究结论与建议

4.1 研究结论

通过对2020年全国数学高考共13套试卷进行定量分析，可以看到新高考与传统高考在多个维度上存在明显差异．下面结合具体的试题，对这些差异进行定性探索，并得到以下研究结论．

（1）新高考对问题情境的设置更具创新性．

难度模型中的“背景”即“情境”．《普通高中数学课程标准（2017年版）》指出，情境主要是指现实情境、数学情境、科学情境，新课标中共出现“情境”一词158次，而实验版课标中仅出现了28次．新课标强调“以主题为引领，使课程内容情境化，促进学科核心素养的落实”，新高考率先体现出了这一新的变化，对问题情境的设置更具有创新性．

新高考Ⅰ卷和新高考Ⅱ卷都各有7道题分别在生活情境、数学文化、社会时事、科学背景进行对数学知识的考查，有背景的试题占比为32%，这在数学高考史上创下了一个新高，说明新一轮高考改革将重视问题情境的设置．李健、童莉为探清中国高考评价体系“四翼”中的“应用性”和“创新性”如何在数学高考中落实，对2020年数学高考试题的问题情境设置进行了分析，并建议教学应关注现实，以真实、实用性的问题情境促进学生学以致用，以陌生、开放式的问题情境开拓学生的思维场域[7]．

（2）新高考对知识的运用更具综合性．

为促进中国课程深化改革，高考已从能力立意转向素养导向，对数学核心素养的测量与评价势在必行．任子朝等人指出：数学核心素养具有基础性、综合性、阶段性与个体差异性，其中综合性是指学生能对其所拥有的数学知识、数学能力、数学态度、数学品质等进行有效整合，融会贯通地解决具有复杂情境的问题[8]．《中国高考评价体系》明确提出将“综合性”作为四大考查要求之一，数据显示2020年新高考卷试题中单独考查一个知识点的题量较传统高考有所降低，考查3个及以上知识点的题量大幅度上升，表明新高考试题已经开始调整试题对知识点综合运用能力的考查力度．

新高考Ⅰ、Ⅱ卷选择题9—12题是多选题，均体现了多选题考查容量大的特点：第9题要求学生熟练掌握圆锥曲线的本质特征，能够区分椭圆、双曲线、圆等常见曲线方程；第10题考查了利用图象确定三角函数的解析式以及诱导公式；第11题综合考查了基本不等式、二次函数、指数函数及对数函数的单调性；第12题在“信息熵”的科学背景下考查了对数函数、对数运算以及不等式的基本性质．新高考卷增设的多选题、开放题等新题型是对四基（基础知识、基本技能、基本思想、基本活动经验）和四能（发现问题、提出问题、分析问题、解决问题）良好考查形式，它强调对多个条件或结论之间的知识内在联系和方法的互通性的把握，能体现学生思维的灵活性和深刻性．新题型对考查学生数学核心素养能起到不可替代的作用，实现了高考功能从能力立意到素养导向的转化．

除了多选题为知识点的综合考查提供了试验田，新高考对知识主题的考查也更加丰富．以立体几何为例，由于上海卷未将立体几何作为大题呈现，故将其余12套试卷立体几何的考点作以下归纳，如表3．

表3 2020年数学高考立体几何大题考点梳理

经此横向比较，发现新高考卷综合考查了立体几何的线面平行的判定和性质、线面垂直的判定和性质、求线面角等知识点，还结合基本不等式，达到了使不同主题内容之间融会贯通的效果．

（3）新高考对逻辑推理能力要求加强．

逻辑推理是从一些事实和命题出发，依据规则推出其他命题的素养，包括从特殊到一般的归纳、类比推理，以及由一般到特殊的演绎推理方式，其中数学运算也是一种演绎推理．高考要求学生能够理解相关概念、命题、定理之间的逻辑关系，并能在具体的情境中结合题目条件探寻解决问题的思路．

由图4可以看到，传统高考试卷的简单推理试题占比更多，而新高考Ⅰ卷中复杂推理题量占55%，这与知识点的综合考查以及复杂情境的设置有关．例如新高考Ⅰ卷选择题第4题以中国古代的日晷为背景，考查线面夹角，涉及平面平行、线面垂直的性质定理．需多次运用演绎推理，结合球体、平面几何知识计算出结果，该题属于中档题，推理过程较复杂．选择题第6题以科学情境新冠状肺炎的传染模型为背景，用大量的文字介绍了流行病传染人数满足的指数函数模型特征，该题的求解需要结合题目条件与已有的知识，结合指数式化对数式的运算法则，边推理边计算．

总的来说，试题的背景因素、运算水平与推理难易程度等因素往往是相互关联的，新颖复杂的背景往往会提供更多的题干信息，学生需要具备良好的数学阅读素养，抽象出题目的本质信息，紧接着在脑海中理清相关概念、命题与定理的逻辑关系，获得清晰地解题思路，最后面对复杂的符号运算，考生还需要一次次利用运算法则进行演绎推理．可见一道试题可以对多种数学核心素养进行考查，这也是数学核心素养综合性特征的体现．

4.2 建议

《国务院关于深化考试招生制度改革的实施意见》指出，高考应依据高校人才选拔要求和国家课程标准，科学设计命题内容，增强基础性、综合性，着重考查学生独立思考和运用所学知识分析问题、解决问题的能力[9]．新高考以素养为导向的考查形式势在必行．为促进传统高考向着靠近新高考结构、难度要求的方向改革，基于研究结论，提出以下几点建议．

（1）为更好地发挥情境在引导素质教育、促进学生全面发展中的作用，激发师生重视社会现实问题、增强数学文化自信，在命题中，应适当结合现实情境或科学情境对知识点进行考查．

（2）鉴于开放性问题在考查学生的思维过程、实践能力和创新意识的优越性，命题时，应包含一定数量的开放性问题和探究性问题．根据新课标要求，开放性问题情境的命制应自然、合理．在评分的过程中应注意公平性和阅卷的可操作性：达到测试的基本要求即可视为满意，对于有所拓展或创新的情况可以适当加分．

（3）命题还要注意提高试卷的区分功能．2013年11月发布的《中共中央关于全面深化改革若干重大问题的决定》指出高考改革的方向：探索全国统考减少科目、不分文理科、外语等科目社会化考试一年多考[10]．改革对数学科目试卷的区分功能提出了更高的要求，教育部考试中心任子朝等人指出，要提高试卷的区分度，首先应该提高试卷考查的目的性，其次，适中的试题难度可以保障试卷的区分度[11]．总的来说，新高考试卷具有“低起点”“多层次”“高落差”的特点，有利于不同层次的学生针对性训练，教师在平时的教学中应充分发挥多选题和结构不良试题的作用．

[1] 教育部考试中心．中国高考评价体系说明[M]．北京：人民教育出版社，2019：6–8．

[2] 以评价体系引领内容改革 以科学情境考查关键能力——2020年高考数学全国卷试题评析[J]．中国考试，2020（8）：29–34．

[3] 武小鹏，张怡．中国和韩国高考数学试题综合难度比较研究[J]．数学教育学报，2018，27（3）：19–24，29．

[4] 李保臻，石烨．中国大陆与台湾地区高考数学试题难度比较研究——以2016—2018年大陆全国卷Ⅰ与台湾指考试题为例[J]．数学教育学报，2020，29（1）：58–64．

[5] 张玉环，周侠．综合难度视角下中法高考数学试题的比较研究——基于2015—2019年中国和法国高考数学试卷[J]．数学教育学报，2020，29（3）：43–50．

[6] 武小鹏，孔企平．基于AHP理论的数学高考试题综合难度模型构建与应用[J]．数学教育学报，2020，29（2）：29–34．

[7] 李健，童莉．高考评价体系中“应用性”与“创新性”要求——基于2020年高考数学试卷中问题情境的分析[J]．基础教育课程，2020（Z2）：18–22．

[8] 任子朝，陈昂，赵轩．数学核心素养评价研究[J]．课程·教材·教法，2018，38（5）：116–121．

[9] 中华人民共和国中央人民政府．国务院关于深化考试招生制度改革的实施意见[EB/OL]．（2014–09–04）[2021–04–20]．http://www.gov.cn/zhengce/content/2014-09/04/content_9065.htm．

[10] 中华人民共和国中央人民政府．中共中央关于全面深化改革若干重大问题的决定[EB/OL]．（2013–11–15）[2021–04–20]．http://www.gov.cn/jrzg/2013-11/15/content_2528179.htm．

[11] 任子朝，关丹丹，佟威，等．高考试卷区分功能的评价方法研究[J]．中国考试，2017（10）：7–12．

A Comparative Study of Items from the New College Entrance Examination and the Traditional College Entrance Examination in 2020

LIU Jing1, ZHOU Si-bo2, WU Zhong-lin3

(1. School of Basic Teaching Department, Southwest Petroleum University, Sichuan Nanchong 637001, China;2. School of Mathematical Sciences, Sichuan Normal University, Sichuan Chengdu 610066, China;3. Sichuan Institute of Education Sciences, SichuanChengdu 610066, China)

Given that 2020 is the first year after the new curriculum standards were released, it is necessary to compare and analyze the difficulty of the new mathematics college entrance examination and the traditional college entrance examination. With the help of the comprehensive difficulty model of the college entrance examination questions formed after multiple improvements by Wu Xiao-peng and Kong Qi-ping, this study coded and analyzed a total of 13 sets of exam papers in the 2020 National Mathematics College Entrance Examination according to seven difficulty factors, including background factors, whether or not the test contains parameters, operation level, reasoning ability, knowledge content, thinking direction, and cognitive level. The results show that the new college entrance examination has some changes in its requirements in background factors, reasoning ability, knowledge content, and cognitive level, and the new college entrance examination pays more attention to the innovation of the context setting and the comprehensive application of knowledge.

mathematics college entrance examination; comprehensive difficulty; comparative research

G632.479

A

1004–9894（2021）06–0026–06

刘静，周思波，吴中林．2020年新高考与传统高考的比较研究——基于高考试题综合难度模型[J]．数学教育学报，2021，30（6）：26-31．

2021–07–03

四川省名师名校长工作室专项课题（重点课题）——基于学科核心素养的中学生数学思维品质提升教学策略研究（四川省教育厅川教函〔2019〕514号）

刘静（1995—），女，四川广安人，助教，硕士，主要从事数学教育研究．

[责任编校：周学智、张楠]