基于高考评价体系的数学试题评析——以2020年“北京卷”“天津卷”“山东卷”为例
2021-12-14胡典顺
梁 玮,刘 清,胡典顺
基于高考评价体系的数学试题评析——以2020年“北京卷”“天津卷”“山东卷”为例
梁 玮1,刘 清2,胡典顺2
(1.华东师范大学 教师教育学院,上海 200062;2.华中师范大学 数学与统计学学院,湖北 武汉 430079)
高考评价体系倡导“价值引领、素养导向、能力为重、知识为基”的综合评价,因此以高考评价体系的理念为导向,构建符合五育并举、立德树人高考目标的试题测评框架.以2020年3份新高考数学试题——北京卷、天津卷和山东卷为例进行测评,并利用多元统计分析方法研究2020年数学新高考的命题特点,分析得出:3套试题的命题思路基本体现高考评价体系的宗旨,但在部分维度上,不同地区试题之间存在显著性差异,对于如数学建模、应用性和创造性等方面,3套试题的考查力度不足.依据结论对教学工作和未来高考命题提出如下建议:创设多样情境,体现数学应用价值;加强创新考查,助力学生全面发展;重视关键能力,凸显学科素养导向;贯彻五育并举,落实立德树人目标.
高考评价体系;数学高考;思考与建议
1 问题提出
2019年11月,教育部考试中心以习近平新时代中国特色社会主义思想为指导,深入贯彻党的教育方针和全国教育大会精神,贯彻落实《国务院关于深化考试招生制度改革的实施意见》(国发〔2014〕35号)与《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》(国办发〔2019〕29号)文件精神,对外正式发布由“一核”“四层”“四翼”组成的中国高考评价体系.高考评价体系是始终以核心价值为引领、立德树人为高考根本任务、系统的、科学的、创新的评价体系,创造性地在高考命题理念上实现了由“知识立意”“能力立意”评价向“价值引领、素养导向、能力为重、知识为基”综合评价的转变.高考评价体系提出了高考的根本任务是立德树人,基本功能是服务选才,引导教学是基础教育对高考的现实需求;以核心价值为引领作用、学科素养为导向作用、确定关键能力和必备知识的重点考查内容,促进核心素养落实,发展素质教育;通过强调基础扎实、融会贯通、学以致用、创新意识和创新思维对高考命题做出要求,把握高考的核心功能,促进学生全面发展[1].高考评价体系的正式发布,也对外传递出从2020年开始,无论是全国卷,还是各省命制的试卷,都将全面对标高考评价体系的信号.此外,高考对教学具有导向性作用,高考试题的呈现特征势必对教学活动和课程改革产生深远的影响,因而更新试题评价和分析策略,将高考评价理念融入评价方法、专注高考的评价功能和试题的层次内涵,可以有效帮助教师理解和处理好评价与教学的关系,引导教育过程走向正态化、积极化,为中国高中数学课程改革提供参考信息.
2 文献综述
近年来,许多学者对数学高考从不同视角进行了研究.比如李勇、徐奉先等[2]提出完善知识、能力和情境的多维框架,因地制宜地展开基于核心素养的高考内容改革;李作滨[3]通过计量分析方法以2018年全国Ⅰ卷为例分析数学核心素养在高考数学试题中的考查情况;教育部考试中心[4]从素养、能力、创新、内容改革和数学文化角度,对2018年高考数学全国卷的若干例题进行解读;任子朝等[5]选取2018年高考数学函数试题为切入点,研究高考对函数的考查特征;张定强、裴阳[6]从数学试卷与课标一致性的研究角度对2017—2018年全国Ⅱ卷与浙江卷进行分析;覃创等[7]利用定量统计,以2019年高考全国Ⅲ卷为例,探析高考试题对核心素养的测评情况;李华[8]等通过构建基于数学核心素养的教育评价表,利用多元统计分析对2019年高考数学全国卷进行测评研究;教育部考试中心[9]在高考评价体系的基础上,重点从科学情境、关键能力、试卷改革等视角对2020年高考数学全国卷进行评析.
综上,已有的相关研究主要从两个方面着手:第一,从数学核心素养维度对高考试题进行评析,分析高考试题在核心素养层面的考查特点,研究形式包括实证研究和理论研究;第二,对高考评价体系进行理论研究和解读,部分学者结合高考试题,以具体试题为例论述新高考对高考评价体系指标的体现,主要研究方式是理论研究.数学学科具有逻辑性、抽象性等特点,对数学高考试题的分析也应从多维度深入挖掘,纯粹地从素养层面去分析评判已不再满足高考综合评价的理念.因此将基于高考评价体系框架,结合数学核心素养,构建数学高考试题测评表,以数据、图表量化的形式分析与评价数学高考试题的设计特点,并检验试题是否达到高考的考查要求,对高考未来命题路径和教学实践工作提出若干思考和建议.
3 研究设计
3.1 研究对象
2020年施行第二批新高考的省市有北京、山东、天津和海南,选取2020年第二批加入新高考的省市,由于高考数学海南卷与山东卷类似,题目和题型等相差不大,故选取北京卷、天津卷和山东卷作为研究对象.
3.2 评价框架的确定
高考评价体系是高考命题的理论基础和实践指南.“一核”为考查目的,是对素质教育中高考核心功能的概括,回答“为什么考”的问题;“四层”为考查内容,是素质教育目标在高考内容中的提炼,回答“考什么”的问题;“四翼”为考查要求,是素质教育的评价维度在高考中的体现,回答“怎么考”的问题[10].这3者具体结构和层次关系如图1所示.

图1 “一核四层四翼”高考评价体系结构
3.3 评价指标体系的确定
为研究高考试题中对“价值引领、素养导向、能力为重、知识为基”综合评价理念的体现,选取中国高考评价体系中的“四层”和“四翼”为评价指标,即“必备知识”“关键能力”“学科素养”“核心价值”和“基础性”“综合性”“应用性”“创新性”.再从指标内涵和定义范围将评价指标分为“宏观指标”和“微观指标”两个大类,具体研究框架如图2所示.
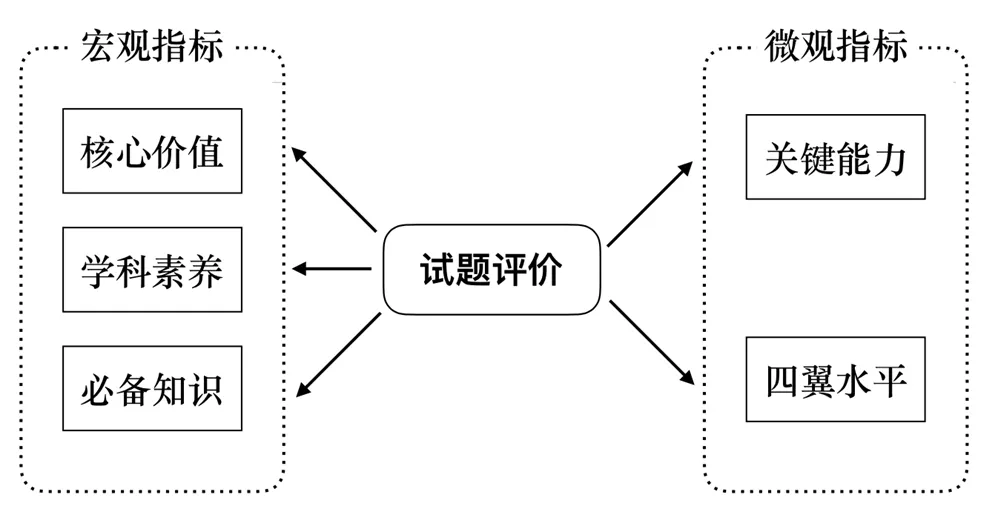
图2 研究框架
3.3.1 宏观指标
根据《中国高考评价体系说明》[1]中提出的核心价值、学科素养和必备知识3个维度,结合于涵、任子朝等[11]对相关概念和内涵的解读,以及《普通高中课程标准(2017年版)》中对数学知识的领域划分,对3个指标进行进一步的二级划分,得到如下宏观指标体系(见表1).

表1 宏观指标体系
3.3.2 微观指标
“关键能力”包含逻辑思维能力、运算求解能力、空间想象能力、数学建模能力和创新能力,从4个角度凸显命题设计对考生不同能力的考查要求.对于数学能力的不同水平划分,PISA模型提出了3种数学过程,即将学生的思维过程和在此中蕴含的数学基本能力划分成数学表述、数学运用和数学阐释3种领域[12];喻平从知识的角度切入,将知识学习的结果分为知识理解、知识迁移和知识创新3种形态,每种形态对应地生成数学关键能力的3种水平[13];徐斌艳提出从内容维度、结构维度和过程维度评价学生的数学核心能力[14].这里将参照这几种测评模型,从问题解决过程中的知识使用状态切入,形成五大关键能力的三级水平划分:直接嵌入式、组合运用式和拓展探究式,具体评价标准见表2.

表2 关键能力的水平划分
注:每一种等级的水平包含本身和比自身低等级水平的要求,如二级水平的要求既包括二级水平本身的要求,也需要具备一级水平的要求.
“四翼水平”既是对数学学科的考查要求,也代表对高考试题的设计要求,从而成为评价高考试题质量和素养水平的重要指标之一.因此,根据任子朝对四翼内涵的深度解读和诠释[11],按照形式、内容、过程的深度和广度,将四翼划分为3种等级水平,构建四翼水平划分标准,具体如表3所示.

表3 四翼水平划分标准
根据表2、表3的水平划分,得到微观指标体系表(见表4).
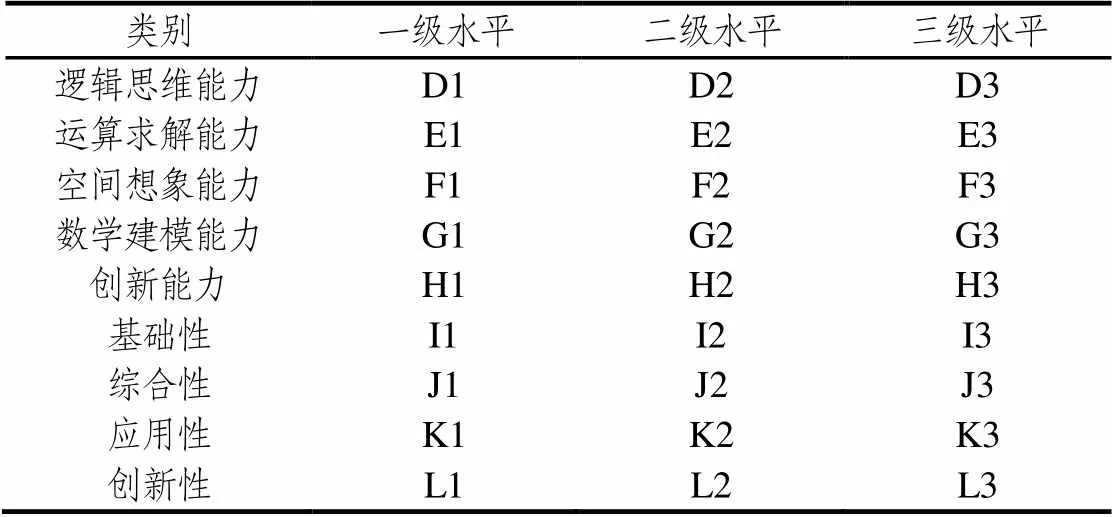
表4 微观指标体系
注:D1代表逻辑思维能力的一级水平,以此类推.
运用上述得出的包含宏观和微观指标的高考试题评价表,对北京卷、天津卷和山东卷中的每一道试题进行详细分析,并将所得结果进行汇总和比较,下面以一道试题为例,对其进行高考试题评价表的测评,给出详细具体的操作演示和说明.
(山东卷第4题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为),地球上一点的纬度是指与地球赤道所在平面所成角,点处的水平面是指过点且与垂直的平面.在点处放置一个日晷,若晷面与赤道所在平面平行,点处的纬度为北纬40°,则晷针与点处的水平面所成角为().

A. 20°B. 40°C. 50°D. 90°
评析:这道试题所创设的试题背景是中国古代用来测定时间的仪器日晷,将数学史和数学文化融入情境,充满鲜明的数学学科特色和数学文化的底蕴熏陶.题目主要考查几何与代数中立体几何的知识,利用面面平行的性质定理和线面垂直的定义判定有关截线的关系,根据点处的纬度,计算出晷针与点处的水平面所成角即可解决.通过新颖有趣的背景,意在引导学生利用数学知识解决实际问题,体会数学的应用之美.同时在审题过程中,需要学生具有理性思维和逻辑推理能力,提取题干中的关键信息,并进行知识建构,基于日晷本身的特点来进行思考,并进行一定程度的探究,因此逻辑推理能力为二级水平;同时该试题需要进行简单的数学运算,并通过简单的数学建模,再通过作图,分析图形之间的关系,辅助解答,故运算求解能力、数学建模能力为一级水平,空间想象能力为二级水平.从四翼水平的角度来看,该道试题考查的多个知识点如“线线垂直”“线面垂直”“面面平行”等的性质、定义、判定,涉及多个核心概念如“平行”“垂直”等,故该试题属于基础性二级水平、综合性二级水平、应用性二级水平和创新性二级水平.测评结果如下(见表5).

表5 例题测评结果
4 研究结果
4.1 3套试卷的宏观分析
为了对3套试卷的宏观指标——核心价值、必备知识和学科素养有一个直观的统计分布了解,利用SPSS 26.0绘制3个维度共12个指标的条形图,如图3所示.

图3 “核心价值”“必备知识”“学科素养”条形图
根据图3可以看到,基于核心价值维度,3套试卷都注重在试题中体现数学学科特色,而对于正确价值导向、爱国精神以及数学文化,北京卷和天津卷均涉及较少,山东卷在这4个指标中都有所体现;基于必备知识维度,3套试卷的考查重点均集中在函数和几何与代数两个领域,3套试卷在预备知识部分的试题量较为均衡,且在试题统计时发现预备知识的题目一般出现在选择和填空的前两题;3套试卷对概率与统计试题一般设计2~3题,与往年的高考试卷相比,题量分布较为稳定.同时根据条形图中的矩形高度,3套试卷在必备知识维度差异较小;基于学科素养维度,3套试卷的命题都重点突出理性思维,山东卷和北京卷在理性思维、数学应用、数学探究与数学文化均有涉及,且相关试题数量相近,同时这两套试卷能够体现数学应用、数学探究的试题数量明显多于天津卷,而天津卷没有涉及到数学文化的试题.
基于条形图的直观分析,为了对3套试卷在核心价值、必备知识和学科素养这3个变量之间的差异进行检验,选择方差分析法,在方差分析的结果中,判断是否具有显著性差异主要看统计量和对应的显著性(也称为值),若值大于0.05(或0.1)则认为变量之间不具有显著性差异,反之认为变量之间具有显著性差异.经检验,3套试卷在核心价值和必备知识维度的值均大于0.05和0.1,因此认为在这两个层面上,3套试卷不具有显著性差异.而对于学科素养维度的分析结果如表6所示.

表6 学科素养方差分析
在满足方差齐性的前提下,北京卷、天津卷和山东卷在学科素养的方差检验中,统计量为3.889,<0.05,说明试卷之间在学科素养维度具有显著性差异,因此可以确定哪几套试卷之前存在差异,故需要做进一步的事后比较,选择分析结果较为直观清晰的S-N-K比较方法,结果如表7所示.
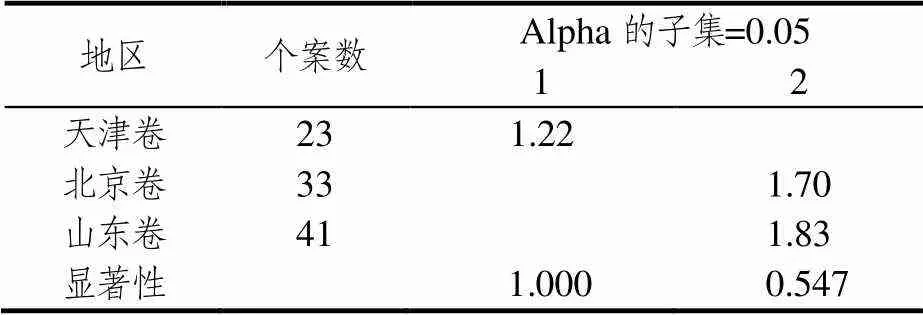
表7 学科素养事后比较
由表7可得,在学科素养维度上可分成两个类别,分别是类别1天津卷,类别2北京卷和山东卷,从结果中可以看出同一组内的变量值大于0.05,不具有显著性差异,而两组别之间存在差异,与上述的条形图分析结果一致.
4.2 3套试卷的微观分析
为了对3套试卷的微观指标——关键能力水平和四翼水平有一个直观的统计分布了解,利用SPSS 26.0绘制9个维度3个水平共27个指标的条形图,如图4所示.
通过图4可以观察到,对于五大关键能力,3套试卷对于前3个关键能力即逻辑思维能力、运算求解能力和空间想象能力都有较为密集的分布,说明这3套试卷的设计都突出了对学生这3种能力的考查,其中对于逻辑推理能力的考查要求重点体现在水平一和水平二层级,对运算求解能力的要求集中在水平二层级,对空间想象能力的要求集中在水平二层级;而对于数学建模能力和创新能力,北京卷和天津卷体现力度不足,甚至没有体现对这两种能力的考查,而山东卷通过创设新颖的情境和多答案、多解法的试题,重视学生的思维过程和解决问题的能力,重视对学生数学建模能力和创新能力的考查.
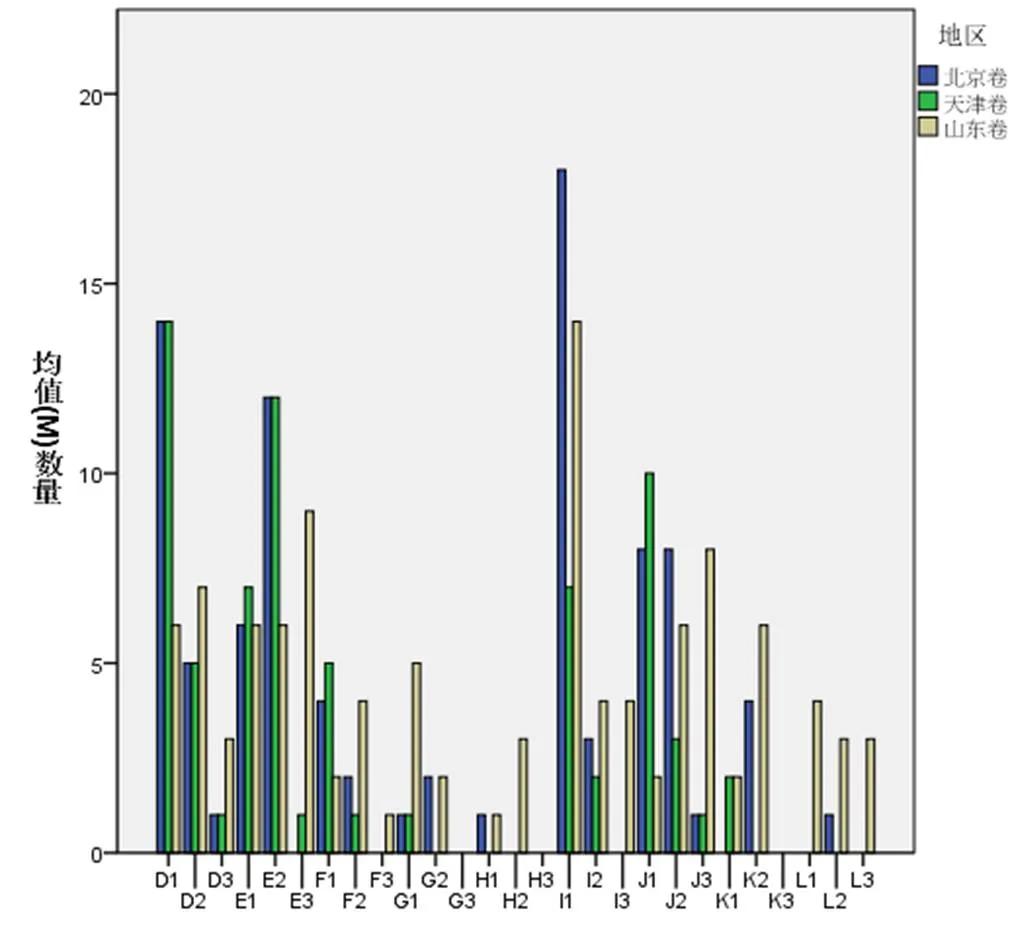
图4 关键能力水平和四翼水平统计分布
对于四翼水平,山东卷对于4个维度的考查要求均有体现,且在3种水平分布上较为均衡.北京卷和山东卷主要凸显了对基础性和综合性的考查要求,北京卷少量试题体现了对应用性和创新性的考查,而天津卷只有少量试题体现了应用性,对于创新性的要求没有体现,同时相较于山东卷,北京卷和天津卷在同种四翼水平的维度下,表现的题量少且水平低,说明这两套试卷在考查学生能否综合应用知识、选择合适的数学模型、创造性地解决问题方面力度不足.
为了进一步比较3套试卷的特点,同样利用SPSS 26.0对关键能力和四翼水平分别进行方差分析,结果显示在满足方差齐性的假设前提下,3套试卷在这两个维度下的方差分析值均小于0.05,因此可以认为这3套试卷在关键能力和四翼水平下具有显著性差异,同样利用S-N-K比较方法进行事后比较,结果如表8、表9所示.
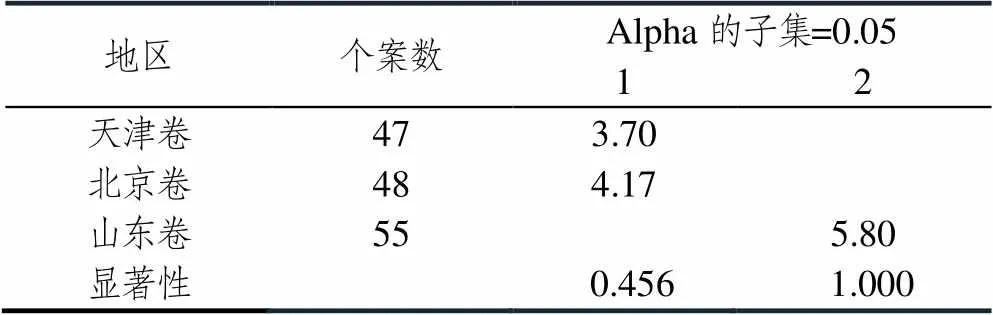
表8 关键能力事后比较
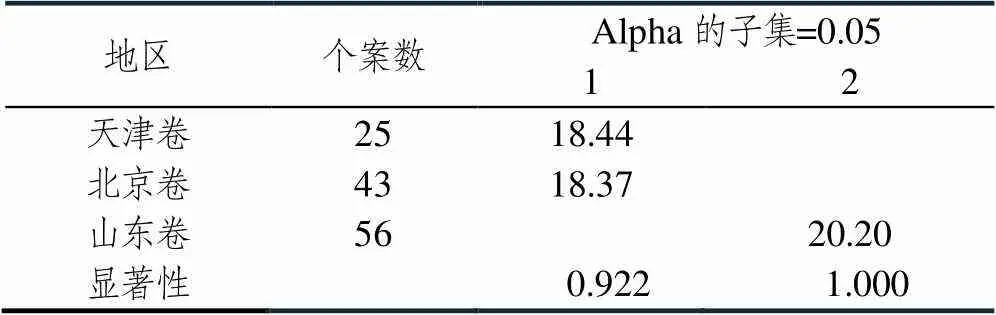
表9 四翼水平事后比较
根据表8、表9可以看到,基于关键能力和四翼水平维度,可以将天津卷和北京卷视为同一类,而山东卷则视为另一类,即天津卷和北京卷在关键能力的考查、四翼水平的设置特点较为相似,而山东卷则与北京卷和天津卷差异较大.
4.3 对关键能力和四翼水平的对应分析
为了进一步探究3套试卷关键能力和四翼水平在空间位置上的分布特征和分散程度,更好地探究维度指标之间的内部关联以及试卷与指标之间的相关程度,利用SPSS 26.0对统计数据进行对应分析,由于研究中的统计测评的数据是频数,因此采取卡方距离来代表相应单元格内平均值偏离无关联假设的程度[15],得到相应的对应分析图(见图5).

图5 对应分析
对应分析法主要观察分析结果中不同变量的分布特征和分散距离,根据图5可以发现,试卷类型、关键能力和四翼水平在空间上整体呈现分散状态,说明这些研究对象在两个维度上都具有一定的区别.按照维度来看,北京卷和天津卷在维度一上区别不大,在维度二上有所不同.山东卷在维度一上距离另外两套试卷较远,在维度二上与另外两套试卷具有一定的区别.27个测量指标整体呈现放射线状分布趋势,内部之间又出现分布聚集的特点.
北京卷和天津卷无论在维度一还是维度二,均远离原点,山东卷在维度一上出于均衡位置,维度二上与原点相差较大,3套试卷之间彼此相距较远,说明这3套试题对关键能力的考查和四翼水平与平均水平区别较大,也反映出3套试题的命题特点各不相同,符合图3条形图的描述.
从关键能力和四翼水平27个层级指标来看,逻辑思维能力D3、运算求解能力E3、空间想象能力F3、创新能力H2、基础性I3、综合性J3和创新性L1散点与山东卷处于同一放射线方向,说明山东卷在这些关键能力和考查要求的水平一和水平三层级高于平均水平;而北京卷处于D3、E3、F3、H2、I3、J3和L1散点的射线反方向,说明北京卷处于这些指标的低层级水平.同时,天津卷与空间想象能力F2、基础性I2和创新性L2散点射线方向相反,说明天津卷在这些指标的体现层级水平不高.
5 结论与建议
5.1 结论
根据上述研究,可以发现3套试卷在核心价值、必备知识维度无显著差异,且核心价值集中表现在数学学科特色层面,必备知识的考查以函数、代数与几何为主,对于预备知识和概率与统计的试题题量和位置分布较为稳定;基于学科素养维度,天津卷与北京卷、山东卷有显著差异,虽然3套试卷均有很大一部分试题集中体现了理性思维,但是在数学应用和数学探究层面,天津卷的考查力度明显弱于北京卷和山东卷,此外,相较于理性思维、数学应用和数学探究,数学文化在3套试卷中的考查力度最弱;基于关键能力维度,山东卷与北京卷、天津卷有显著差异.3套试卷均突出了对逻辑思维能力、运算求解能力和空间想象能力的考查,考查水平多为水平二,对于数学建模能力和创新能力,山东卷的考查力度强于北京卷和天津卷,且3套试卷对于数学建模能力和创新能力的考查水平集中在水平一和水平二;基于四翼水平维度,山东卷与北京卷、天津卷有显著差异.山东卷试题在基础性、综合性、应用性与创新性4个层面均有体现,且考查水平较为均衡,北京卷和山东卷主要凸显了对基础性和综合性的考查要求,应用性与创新性涉及较少.
5.2 建议
5.2.1 创设多样情境 体现数学应用价值
通过上述研究分析,可以看到3套试卷主要体现了理性思维,同时山东卷还注重对数学应用和数学文化的表现,但北京卷和天津卷对于数学应用的体现相对缺乏.《普通高中数学课程标准(2017年版)》及新高考的考查目标中,都注重利用真实的情境让学生知晓如何用数学来解决实际问题[11].从近几年数学高考的试题分析中不难发现,试题情境化将成为高考命题的趋势和常态.真实、复杂、创新的问题情境,会给考生带来题目更长、阅读量更大、信息更冗杂的审题挑战,这样的转变导致对学生的阅读审题能力和数学抽象能力的要求有了更大的提高,因此教师可以通过加强日常审题教学,创设真实多样的教学情境,提出合理的数学问题,帮助学生感受情境与问题的联系,改变只刷题不思考的机械模式,引导学生读题、说题,帮助提高学生提取信息的能力,抓住问题解决的关键.同时试题情境化也符合数学一直强调的“学以致用”,因而教学工作者在教学实践中应不断加强学生的数学应用意识,在教学内容的基础上,将生活中的问题数学化,创设现实情境开展教学活动,让学生多多了解生活中的数学模型,更深刻地感受数学价值,提升运用数学思想方法和数学建模解决实际问题的能力.
5.2.2 加强创新考查 助力学生全面发展
通过3套试卷的评析可以看到,山东卷相比北京卷和天津卷在题型的设置方面有比较大的不同,山东卷选择题第9、10、11、12题为多选题,解答题第17题还具有一定的开放性,这样的题型体现了一定的创新性,响应了“一核四层四翼”高考评价体系中对创新性题目的设置要求,考查学生对数学知识灵活运用的能力.在应试教育环境下,题海战术和套路训练常见于中学学习中,这显然并不是高考所希望的.创新性试题如开放性试题、结构不良试题等,正是由于其新颖、不多见,能够打破学生数学学习中的定势思维,考查学生综合运用知识的能力,更好地促进学生的全面发展.
5.2.3 重视关键能力 凸显学科素养导向
从上述研究中可以强烈地感受到2020年高考数学试卷对考生关键能力和学科素养的重视,尤其对逻辑思维、运算求解和空间想象的考核在试卷中得到了充分的体现,同时加强了对于批判性思维、阅读理解、信息整理、语言表达等能力的考查.学科素养的训练是一个潜移默化的渗透过程,需要教师在教学中以素养为导向,选择合适的教学内容和教学手段,营造适合培养学科素养的教学氛围,不断向学生传导数学方法、思想、意识,同时对于数学思维和关键能力的训练不仅仅局限于解题过程,还可以推广至形如问题引入、审题分析、推导解答、反思拓展等教学实践过程中.
5.2.4 贯彻五育并举 落实立德树人目标
2020年新高考数学坚持高考的核心价值,具有鲜明的学科特色和时代特色.除了上述山东卷第4题的日晷问题,3套试卷中的其它题目也体现出中国社会主义建设成就、科学防疫成果和文化底蕴,通过创新题型设计,紧密联系社会实际,创设真实问题情境,向学生传达积极正确的价值取向、民族意识和时代精神,同时在试题中引入世界数学背景、民族历史精华,不仅蕴含深厚的文化积淀,培养学生家国情怀的同时,不忘开拓学生的数学眼界,数学学习道阻且长,学无止境,以期学子们步履不停,鹏飞展翅,充分发挥高考立德树人的育人价值.
[1] 教育部考试中心.中国高考评价体系说明[M].北京:人民教育出版社,2019:1–4.
[2] 李勇,徐奉先,赵静宇,等.基于核心素养的高考内容改革理念及路径[J].课程·教材·教法,2019,39(7):76–83.
[3] 李作滨.素养导向的数学测评研究——以2018年高考为例[J].数学教育学报,2018,27(6):33–37.
[4] 教育部考试中心.素养导向新举措 能力考查新突破——2018年高考数学试题评析[J].中国考试,2018(7):8–12.
[5] 任子朝,赵轩.突出基础性综合性 发挥区分选拔功能——2018年高考数学函数试题分析[J].中国考试,2018(11):62–65.
[6] 张定强,裴阳.新高考改革背景下数学试卷与课标一致性研究——以2017—2018年全国Ⅱ卷与浙江卷为例[J].数学教育学报,2019,28(4):55–60.
[7] 覃创,严忠权.核心素养为导向的数学测评研究——以2019年高考全国Ⅲ卷为例[J].数学教育学报,2020,29(2):24–28.
[8] 李华,胡典顺.基于数学核心素养评价框架的试卷测评研究——以2019年高考全国卷为例[J].数学教育学报,2020,29(2):18–23.
[9] 教育部考试中心.以评价体系引领内容改革 以科学情境考查关键能力——2020年高考数学全国卷试题评析[J].中国考试,2020(8):29–34.
[10] 于涵.新时代的高考定位与内容改革实施路径[J].中国考试,2019(1):1–9.
[11] 于涵,任子朝,陈昂,等.新高考数学科考核目标与考查要求研究[J].课程·教材·教法,2018,38(6):21–26.
[12] OCDE. PISA 2012 Assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy [M]. Paris: OECD Publishing, 2013: 28.
[13] 喻平.基于核心素养的高中数学课程目标与学业评价[J].课程·教材·教法,2018,38(1):80–85.
[14] 徐斌艳.数学核心能力研究[M].上海:华东师范大学出版社,2019:160.
[15] 张文彤,董伟.统计分析高级教程[M].北京:高等教育出版社,2018:275.
An Analysis of Mathematical Items in College Entrance Examination Based on the New Framework of the College Entrance Examination——With a Focus on Taking 2020 Mathematics College Entrance Examination from Beijing, Tianjin, and Shandong
LIANG Wei1, LIU Qing2, HU Dian-shun2
(1. College of Teacher Education, East China Normal University, Shanghai 200062, China;2. School of Mathematics and Statistics, Central China Normal University, Hubei Wuhan 430079, China)
The college entrance examination evaluation system advocates a comprehensive evaluation that is “value-oriented, literacy-oriented, ability-oriented, and knowledge-based.” Therefore, the guiding concept of the college entrance examination evaluation system is to build a test question evaluation framework that meets the goals of educating in the five domains simultaneously as well as in morality. Taking three new mathematics examination questions in 2020—Beijing, Tianjin, and Shandong examinations as examples—we used multivariate statistical analysis methods to study the characteristics of the propositions of the 2020 mathematics examinations and reached the following conclusions: the proposition ideas of the sets of examinations basically reflect the purpose of the college entrance examination evaluation system, but in some dimensions, there are significant differences among different regions, and the sets of examinations are insufficient in terms of mathematical modeling, application, and creativity. Based on these conclusions, the following suggestions are made for teaching work and future college entrance examination propositions: Create diverse scenarios to reflect the application value of mathematics; strengthen innovation and examination to help students develop in a well-rounded way; focus on key abilities and highlight the orientation of subject literacy; and implement the education of five domains simultaneously as well as implement the goal of morality education.
evaluation system of college entrance examination; mathematics examination for college entrance; thoughts and suggestions
G632.479
A
1004–9894(2021)06–0020–06
梁玮,刘清,胡典顺.基于高考评价体系的数学试题评析——以2020年“北京卷”“天津卷”“山东卷”为例[J].数学教育学报,2021,30(6):20-25.
2021–08–22
教育部人文社会科学研究规划基金项目——中小学核心素养测评的模型建构与实证研究(19YJA880012);中央高校基本科研业务费专项资金资助——基于学习分析技术的高中数学核心素养评价模型研究(CCNU19TS029);中央高校基本科研业务费项目“教师教育专项”(CCNUTE2020-04)
梁玮(1995—),女,江苏扬州人,博士生,主要从事数学课程与数学教学研究.
[责任编校:周学智、陈汉君]
