高考课标卷概率统计试题的特点及其教学启示——基于2011—2020年全国课标卷的分析

李亚琼，徐文彬

高考课标卷概率统计试题的特点及其教学启示——基于2011—2020年全国课标卷的分析

李亚琼1，2，徐文彬1

（1．南京师范大学 课程与教学研究所，江苏 南京 210079；2．南京艺术学院附属中等艺术学校，江苏 南京 210013）

基于2011—2020年52套全国课标卷，从考查总分、考查知识、试题特点和命题导向4个方面对课标卷中概率统计试题特点进行了统计与分析．概率统计试题在全国卷中考查总分占比呈增加趋势．具体而言，侧重用数据呈现的规律解释随机现象，用概率或统计模型表达随机现象的统计规律；情境的创新融入了综合化的新趋势；重视概率与函数、概率与不等式、概率与数列等交汇知识在试题中的融合考查；呈现出重视数学文化渗透、问题情境载入和知识融合创新的命题导向．基于高考对教学的导向作用，概率统计专题教学应重视：研究新课标，关注新旧过渡；回归教材，重视知识的整体结构性；基于学情，加强学生“四能”培养；落实教学，尝试“整—分—联”教学思路．

高考课标卷；概率统计；试题特点；整体教学；“整—分—联”教学思路

概率统计是研究随机现象数量规律的数学学科，包括通过有效地收集、整理和分析相关数据，从而对所考查的问题做出推断和预测[1]．陈希孺在《概率论与数理统计》中提到：从实用的角度来看，概率的统计定义是一种通过实验去估计事件概率的方法，而统计是研究怎样收集数据，并对数据进行分析，进而对研究的问题进行推断的方法．概率统计知识是高中数学学习的重要内容之一，2000年高考试卷中首次出现概率试题，2001年高考试卷中出现统计试题，2004年高中教材中大量增加概率统计内容，考查题型、考查方式等有了较大的变化[1]．《普通高中数学课程标准（2017年版）》（以下简称新课标）中提到：概率的研究对象是随机现象，引导人们从不确定性的角度认识客观世界，同时提供重要的思维模式和解决问题的方法．统计的对象是数据，核心是数据分析，概率为统计的发展提供理论基础[2]．总之，对概率统计的考查已由摸索、稳定进入到创新的阶段．

1 问题提出

传统概率统计教学中，往往重视概率统计的科学工具性价值，而忽视其文化内涵与育人功能[3]．2014年启动的新高考方案，提出了文理不分科的新要求．高中文理科学生的较大差异体现在空间想象能力和数据处理能力，与之相应的知识内容是立体几何和概率统计[4]．新课标将“数据分析”作为高中数学课程目标中培养学生所必备的数学素养之一，这既凸显高中课程中概率统计内容的教育价值，也是对概率统计的育人价值提出更高的要求．高考实行不分文理科的改革后，数学科考试中概率统计的定位、考查内容和形式以及考生群体和水平都会随之发生变化，所以需要研究概率统计试题、试卷结构和难度要求等[5]，结合试题研究回归课标目标要求、落实课标教学目标、开展有效教学[6]，发挥新高考数学科对中学数学教学的积极导向作用，以期促进学生实现自我发展．

新高考数学科概率统计试题有哪些特点？新课标在概率统计的考查要求上作了哪些变化？新高考概率统计的导向教学作用可能体现在哪里？研究者结合2011—2020年全国卷（其中包含2020年新高考卷），汇总了这10年的全国Ⅰ、Ⅱ、Ⅲ文理卷和2020年的新高考Ⅰ、Ⅱ卷共52套试卷（其中2011—2015年共20套、2016—2019年共24套及2020年共8套），并对比了不同时期全国卷概率统计考查的题型和分值，研读新课标中对概率统计的要求．基于高考导向教学，引起教学上的重视，加大概率统计在教育教学中的贡献[3]．

2 概率统计试题的特点

结合近10年全国课标卷，梳理出高考概率统计部分的考查知识及对应分值（具体可参见附录），需要说明的是，因计数原理、排列组合及二项式定理较概率统计知识具有相对独立性，故这3部分不在附表统计范围之内，以下分析中不再说明．

2.1 总体特点

从历年试题统计可以看出：试题在考查概率与统计知识的同时，更侧重于问题情境的嵌入以及思想方法的渗透．

（1）从考查总分来看：该专题考查总分17分的出现37次，总分22分的出现9次，总分12分的出现6次，试题的题量、题型、分值均有适度的变化，总体趋势是选填题考查1题左右和解答题考查1题，以中档题或中档偏易题为主，考查总分约占全卷总分的12%左右．

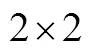
对选填题的知识统计（如表1所示）表明，52套试卷中共考查了56道选填题，其中有22次考查古典或几何概型；统计图分析（如频率分布直方图、饼形图、柱形图、折线图、茎叶图、气温雷达图等）、抽样及样本估计、互斥事件及独立事件概率共考查29次；随机变量分布列及其数字特征、回归方程或相关系数共考查5次．由此可以看出，文理卷在选填题上均侧重考查古典概型、抽样及样本估计、统计图分析及互斥或独立事件概率．

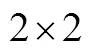
表1 2011—2020年全国课标卷概率统计（选填题） 知识考查次数分布

表2 2011—2020年全国课标卷概率统计（解答题） 知识考查次数分布

注：由于解答题考查的综合性，表中对相关知识进行了融合统计，共统计4个知识的考查情况．其中将“互斥或独立事件概率”并入“随机变量”进行统计；因为统计图分析的工具性作用及知识交叉考查特点，以主要考查知识来统计次数，比如“统计图分析”与“回归分析”结合考查时，记入“回归分析”；“统计图分析”与“样本估计”结合考查时，记入“抽样及样本估计”．

2.2 试题特点

结合近10年52套全国卷的研究，对高考概率统计的考查进行了总体分析，基于此，将继续进行试题考查特点的分析．

2.2.1 重视基础知识的变式考查

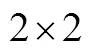
2.2.2 重视问题情境的创新考查

新课标在划分学业质量水平时，首先考虑了“情境与问题”，可见高考对数学素养的考查需要在一定情境中进行[7]．而通过对近10年全国课标卷概率统计试题的研究发现：试题重视情境的创设和问题的提出，这与新课标的要求相契合，也是以后研究需要继续关注的．

所分析的52套试卷中，共计考查109道概率统计题（同一年文理卷出现题目相同均重复计算）．依据新课标对情境进行划分：现实情境、数学情境和科学情境[2]．由表3知：现实情境考查了94次，占比达86.2%；数学情境考查了11次；科学情境考查了4次．由此可以看出解答题及客观题以现实为情境较多，主要考查考生的分析问题、解决问题的能力（以例1—例3来举例说明）．

表3 2011—2020年概率统计试题的“情境”分布

例1 （2012年全国Ⅰ卷·理15）

例2 （2018年全国Ⅱ卷·理8）

例3 （2020年全国Ⅰ卷·理5）

以上3个例子中，例1是以科学情境融入考查正态分布，例2是以数学情境为背景考查古典概型，例3考查现实情境背景下的回归分析，这3个例子均考查学生对新情境的学习能力、结合新情境及相关统计知识解决问题的能力．

2.2.3 重视数学建模能力的考查

历年课标卷概率统计考查学生能根据实际问题正确建立概率模型，并能在实际问题中加以解释，将数学解答转化成对现实对象的分析．当然对概率的考查不应只停留在概率计算的层面，其出发点和归宿都是解决问题，即能够利用计算结果为决策提出关键性的依据．而对统计的考查侧重于用样本数字特征对总体进行估计，考查样本估计总体的统计思想[8]．

近10年全国卷中，概率统计试题多以现实情境为背景，这就要求学生能够从数学的视角去发现问题、提出问题、分析问题、构建模型、计算结果及依据结果提出决策．全国卷重视对学生数学建模能力的考查，而概率统计的知识与现实生活和科技发展紧密相关，具有较强的理论性和应用性，是数学模型的重要载体[1]．

2.3 命题导向分析

以全国课标卷概率统计试题的统计数据为基础，结合统计图分析及试题特点[9]，将继续探讨命题导向启示，具体分析如下．

2.3.1 知识融合创新

结合表4和图1可以看出，概率统计考查总分占比呈增加趋势．随着文理不分科的实行，概率统计命题有了综合化的趋势，重视概率与函数、概率与不等式、概率与数列等交汇知识在试题中的融合考查．知识点考查上，加大了学科间知识融合命题，注重随机思想、抽样思想、或然与必然思想[10]；注重与情境的结合，突出概率统计在解决实际问题中的作用．素养考查上，侧重理解抽样方法的统计意义，侧重考查用数据呈现的规律来解释随机现象，侧重用概率或统计模型来表达随机现象的统计规律．

2.3.2 数学文化渗透

高考概率统计试题重视考查数据分析和统计素养的同时，也重视数学文化的育人价值．数学学习的主要目的是引导学生形成逻辑思维能力和形象思维能力，形象思维是先导，逻辑思维是核心．试题通过渗透数学文化背景，如音乐中的数学、体育中的数学、数学史料等，重视形象思维和逻辑思维的有机融合，在形象思维的基础上增强学生的理性思维能力，培养学生从感性走向理性，从而走向以文化人的目标．

表4 2011—2020年概率统计试题的考查总分均值分布

图1 2011—2020年考查分值均值变化趋势

2.3.3 问题情境载入

情境是高考实现价值引领、素养导向、能力为重、知识为基的综合考查载体，高考试题以知识为基础，情境为载体，从而可以实现考查目的与形式的统一[11]．概率统计试题中情境载入目的是：引导学生能进行模型识别、现象解释并据此提供决策；能够在熟悉的数学情境中，选择合适的抽样方法去收集数据，选择合适的概率模型去分析数据等；能够在关联的现实情境中，选择合适的随机变量刻画随机现象，理解抽样方法的统计意义，运用适当的概率或统计模型表达随机现象的统计规律；能够在综合的情境中，结合数据规律，理解统计意义并做出合适的统计决策．当然，为保证试题情境能够发挥准确价值，情境创设时需要遵循真实性、简洁性、公平性和一致性[12]．

3 结合试题分析 启示教学实践

如何将知识融合创新、数学文化渗透及问题情境载入有机结合并能运用于教学？结合新旧课标的变化比较，提出新课标下的概率统计的教学启示．

3.1 研究课标 关注新旧过渡

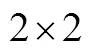
3.2 回归教材 重视知识的整体结构性

概率统计试题重视基础概念，预示教学要回归教材．教材中，关于概率统计专题的知识点较为分散，前后知识交叉排列．新课标重视数学科知识体系结构化，这就需要教师结合课标回归教材，关注概率统计的整体性，系统地进行单元整体教学[13]．当然，整体性需要教师关注知识的层次性，教材知识逻辑与学科知识逻辑的关联性，及教师对主题知识的整体结构把握[14]，即概率统计知识整体性体现为层次性、关联性和结构化．于是研究中结合对新课标的解读，将教材中概率统计的内容进行了结构化梳理（如图2所示）．需要说明，从知识的整体性考虑，结构图中包含了计数原理和二项式定理的内容．

图2 2017版课标中概率统计内容的整体结构

3.2.1 知识的层次性

图2纵向关注了概率统计知识的结构层次及知识融合，横向关注了必修内容和选择性必修内容的衔接，体现知识的螺旋式上升．比如统计的目的是服务于概率，这个结构图能较好地呈现统计知识与概率知识的内在关系．由随机试验、随机事件、事件的关系自然呈现接下来的知识点——概率运算、随机变量等，体现知识的动态生成性与层次性．

3.2.2 知识的关联性

从图2可以看出，“整理、分析数据”和“表达与解释”共同为研究“样本估计”和“相关关系”作铺垫．另外，随机变量的本质是样本统计量，而利用样本统计量又可以进行样本估计和相关系数的研究，这样可以明确知识间的关联性，使得知识系统更加清晰．比如，由随机事件及古典概型到计数原理再到随机变量，这3块知识如何融合过渡？需要教师去思考．再比如必修教材中，在相关系数部分涉及线性回归分析，在选择性必修时会继续涉及更一般的回归分析以及独立性检验，所以教师需要关注到知识的关联性和层次性去组织教学．

3.2.3 知识的结构化

了解知识整体结构图（如图2所示）是教师进行整体教学的前提，需要教师对知识进行整体把握，理解知识体系中直观和严谨的关系[15]，厘清知识间的联系以及同一部分内容中知识的关联性和层次性，最后呈现出结构化知识体系，再用于教学实践．因此，回归教材预示教师首先要回归教材中的知识内容，消化理解内容蕴含的层次性、关联性和结构化．教师只有站在这样的整体视角，才能更好地实施从教到学，在教学中才能关注到概率统计内容的人文价值渗透．

3.3 基于学情 加强学生“四能”培养

高考的导向作用启示教师在进行整体教学的同时，也要关注学生的“四能”培养[16]．教师在教学中需要关注：

（1）关注学生审题能力，提升学生的数学抽象与直观想象的数学素养，培养学生发现问题和提出问题的能力；（2）渗透培养数学建模能力，引导学生根据实际问题构建概率模型，分析数据，提升学生数据分析和数学建模能力，培养学生分析问题解决问题的能力；（3）重视数据计算，规范学生的解题习惯和思维训练，提升学生的逻辑推理和数学运算能力，培养学生解决问题的能力．解题中应体现数学模型化、综合应用性，强调从知识能力立意转向统计素养立意．统计素养是学生在掌握知识能力的基础上，经过反复实践与反思而后逐渐深化形成[17]，于是在教学中需要渗透思维训练，培养学生统计学习兴趣和提升其统计素养．

3.4 落实教学 尝试“整—分—联”教学思路

概率统计知识的整体教学需要教师从章节或单元的角度对教学内容重构，根据章节中不同知识点的教学要求及学生的特点，转化为符合学生实际的教学结构安排．教学安排上，需要关注学习内容与学习方式是否适应学生的能力要求[14]．结合历年试题的分析及课标中内容的变化，探讨整体视角下对概率统计内容的教学思路，具体包括3个方面．

（1）突出层次，整合教学内容．教师在进行整体教学前，需要进行如图2的知识梳理．然后教师在教学中才能关注到知识的生长性、必修和选择性必修中相应知识的联结性．

（2）突出重点，分解教学内容．教师在进行专题教学中，需要做好知识的再现与深化，教学中需要渗透思想方法、需要关注确定性思维和统计思维的差异、归纳推断与演绎证明的区别，理解统计推断结果的或然性．比如，条件概率是含参变量的集合函数，是概率的推广[18]．教师在教授条件概率时，需要从概念的本质出发，解释条件概率的理论价值，激发学生学习条件概率的兴趣，从而更好地指导教学．（3）设计活动，联结教学内容．概率统计试题在重基础的同时，题型灵活、知识交汇、不断渗透应用与创新，所以教师应该设计典型案例开展教学活动，在案例教学中提炼出时代特色的应用情境，引导学生关注经济、科技、人文等方面的信息．

综上所述，在教学中关注“数学文化渗透、问题情境载入及知识融合创新”的有机结合，需要教师：基于学情，以加强学生“四能”培养为目标追求，以课标、教材、知识的整体结构性为关键，从而达到“整—分—联”教学思路，这样才是高考数学科对教学的正确导向．

4 小结

高考评价体系是包括“核心价值、学科素养、关键能力、必备知识”在内的高考考查内容体系，是实现“招—考—教—学”各个环节无缝衔接、良性互动的关键，也是发挥高考正向积极导向作用的基础[19]．基于高考评价体系的意义和原则，对全国课标卷的研究可以起到较好的教学启示．所以，高中概率统计教学需要关注新旧课标中相应内容的变化，比如，新课标中强调，概率统计内容应关注运用数据分析解决实际问题，重视统计思维和确定性思维的差异，关注理解统计结果解释实际问题等．当然，教学更需要回归教材重视概率统计知识的整体结构性，需要基于学情落实“整—分—联”教学思路，从而提升学生统计素养．总之，教师需要结合课标变化和历年课标卷概率统计试题的特点，在教学内容上做出整体规划，做好新旧平稳过渡．

[1] 赵轩，任子朝．高考概率统计试题考查目标的沿革与实现[J]．数学通报，2019，58（10）：39–43．

[2] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：30–31，70，75．

[3] 蔺云．哲学与文化视角下概率统计课的育人功能[J]．数学教育学报，2002，11（2）：24–26，102．

[4] 张远增．高考数学不分文理科的探索[J]．中国考试，2019（5）：6–15．

[5] 任子朝，陈昂，黄熙彤，等．高考数学新题型试卷质量分析研究[J]．数学教育学报，2019，28（1）：1–7，48．

[6] 张定强，裴阳．新高考改革背景下数学试卷与课标一致性研究[J]．数学教育学报，2019，28（4）：55–60．

[7] 胡凤娟．“概率与统计”在高考中的定位与考查研究[J]．基础教育课程，2019（15）：14–21．

[8] 周远方，余锦银．2014年高考“概率与统计、计数原理”专题分析[J]．中国数学教育，2014（7–8）：106–119，127．

[9] 任子朝，赵轩，关丹丹，等．图形分析法在高考试题评价中的应用研究[J]．数学教育学报，2021，30（1）：37–41．

[10] 王雅琪．谈高考中概率与统计的考查[J]．数学通报，2016，55（4）：42–46．

[11] 覃创，严忠权，李敏．落实素养为本的高考测评研究——以2020年全国Ⅰ卷数学为例[J]．数学教育学报，2020，29（6）：21–24．

[12] 常毓喜．中学数学教学如何应对高考考试内容的变化以及核心素养的提出[J]．中国考试，2017（2）：52–58．

[13] 浦叙德，颜延亮．例谈单元整体教学中的“首呼、中联、尾应”[J]．中学数学教学参考，2018（5）：50–52．

[14]徐文彬，彭亮，任利平，等．小学数学教材中“认识三角形和四边形”的内容编排分析与比较——以“人教版”“苏教版”“北师版”为例[J]．数学教育学报，2021，30（2）：1–7．

[15] 杨怡，梁会芳，张定强．“数学探究”研究二十年：回顾经验展望[J]．数学教育学报，2020，29（6）：40–45．

[16] 徐颖．“分”“合”“联”，整体设计三角形单元教学[J]．中国数学教育，2019（12）：17–20．

[17] 严卿，喻平．初中生逻辑推理能力的现状调查[J]．数学教育学报，2021，30（1）：49–53，78．

[18] 李杰民，廖运章．条件概率的本质及其教学建议[J]．数学教育学报，2021，30（1）：54–60．

[19] 教育部考试中心．中国高考评价体系[M]．北京：人民教育出版社，2019：3．

An Analysis of Items Related to Probability and Statistics in College Entrance Examinations from 2011—2020

LI Ya-qiong1, 2, XU Wen-bin1

(1. Curriculum and Teaching Institute, Nanjing Normal University, Jiangsu Nanjing 210079, China;2. Secondary Art School Affiliated to Nanjing University of Arts, Jiangsu Nanjing 210013, China)

Based on 52 sets of national course standard papers from 2011 to 2020, statistics and analysis of the characteristics of the probability and statistics test questions in the papers was carried out along four aspects: the total score of the test, the knowledge assessed on the test, the characteristics of the test questions, and the proposition orientation. The proportion of probability and statistics tests in the national papers is increasing. Specifically, the emphasis is on using the laws presented by data to explain random phenomena, and probability or statistical models are used to express the statistical laws of random phenomena; the integration of situational innovation has a new trend of integration; emphasis on probability and function integrate examination of the intersection of knowledge, probability and inequality, probability and sequence of numbers, etc.; present a proposition orientation that emphasizes the penetration of mathematics culture, the loading of problem situations, and the innovation of knowledge integration. Based on the guiding role of the college entrance examination for teaching, the teaching of probability and statistics should pay attention to the following: studying the new curriculum standards and transitioning between the new and the old; returning to the textbook and emphasizing the holistic structure of knowledge; based on the academic conditions, strengthening the training of students’ “four abilities”; implementing teaching and trying the teaching ideas of “integral-sub- union.”

college entrance examination papers; probability statistics; characteristics of test questions; holistic teaching; teaching ideas of “integral-sub-union”

附录：2011—2020年全国卷概率统计试题统计汇总