中国三十年来小学阶段分数研究文献的系统分析及启示
2021-12-14黄晓林黄秦安
黄晓林,黄秦安
中国三十年来小学阶段分数研究文献的系统分析及启示
黄晓林,黄秦安
(陕西师范大学 数学与统计学院,陕西 西安 710119)
文献系统分析发现,围绕教与学形成侧重作为知识的分数和关注分数认知事实两条不同研究主线,且偶有交叉,反映了传统教育“教学围绕教师发生”特点的影响.以分数教学研究为透镜,探讨以学生分数认知为基础进行教材编排,由测量模型引入分数概念的可行性,体现教育研究对学生学习的真切关怀.提出基于“学”展开数学知识探讨以丰富知识内涵;关注学生学习发生真实过程以改进教学实践;深化数学学习评价以促进学生核心素养培养;强化教师数学教学观以指导教学实践研究,为数学教育提供借鉴.
分数概念;分数教与学;教材编写;测量模型
对“数”的认识与学习是小学数学阶段的重要内容,学生的学习“不仅包括数学结果,也包括数学结果形成的过程和蕴涵的数学思想方法”[1].相对于自然数而言,分数的学习明显地表现出“承上启下”的性质[2].分数异于自然数的符号特征与其自身丰富内涵增加了学生学习的难度.无论从数系扩张的角度,把握分数作为数的本质属性,兼顾其产生的历史进程及教学启示;还是从学生数学思维发展的角度,理解学生分数认知规律,为学习与发展构建基础,都对分数学习产生重要影响.因此,不难理解分数作为小学数学教学中一个具体内容,却引起了心理学和教育学学术研究者、教研员和一线教师的广泛关注.近30年来,研究者透过不同的视角,采用不同的策略与方法,在教学实践与学术研究中成果丰硕.作为数学教育领域众多重要议题中的一个,其研究结果中既有作为分数教学内容特有的典型特征,也有中国基础教育阶段共有的特点,以此审视小学数学的“教”与“学”,进行分数研究知识脉络的系统分析,为后续数学教育研究积累些许经验是有意义的.
选取CNKI收录的732篇(其中57篇核心期刊来源文献)小学阶段分数研究文献,采用系统分析的方法,梳理了分数主题研究的知识发展脉络,勾勒知识演进过程;聚焦分数研究的核心问题,审视分数教学研究是否符合学生的认知发展和教育目标;探讨学生“学”与教师“教”之间怎样实现更好的互动,以推动学生自主学习,实现全面发展.
1 中国近30年分数研究主题文献要素的整体分析
从作者身份上看,将研究者分为,一线教师为主的教学实践者、教研员为主的教师教育者、高校教师为主的学术研究者3类.从研究涉及的内容上看,具有典型特征的教学实践者关注到了分数教学的几乎全部内容,编码频次由高到底分别是分数的运算、分数的应用、分数的认识、分数的意义、分数基本性质以及分数的表示.在这些工作中,教师尝试以具体知识内容为载体探讨分数教学问题.而学术研究者的工作中,少部分同教学实践者一样,聚焦分数具体知识,如分数运算中的除法、分数大小的比较、解分数应用题;多数工作关注分数概念的本质含义,在教材中的编排与呈现,儿童分数认知发展.
从研究视角上看,教学实践者多借助具体的教学设计和课堂实录进行教学片段分析、课堂教学活动反思,阐释教学案例背后的教学方法和理念,且具有较高同质性.相反,学术研究者较少关注具体内容的教学实践问题,而是通过分数概念内涵的探讨、教材比较等方式获得对分数本质的认识;关注学生学习中分数概念的理解、发展与建构,以及对学习结果的评价;基于心理学科视角,对儿童学习分数概念的认知思维、表征方式、学习加工模式等进行实证研究.
2 分数研究的知识演进脉络分析
从分数研究的文献增长量上考察分数相关研究的整体进展,发现1991—2000的10年间仅6篇文献在核心期刊上发表,主要研究工作集中在2006—2020年.以《小学数学参考》连续26年的发文量与所检索到的核心期刊文献数量变化比较发现,进入21世纪后关于分数的研究似乎淡出了研究者的视野.其中,2000—2005年检索CSSCI期刊文献数量为0.尽管2006年前15年发表在核心期刊上的文献不多,但研究工作呈现出聚焦学生分数学习的特征:一类关注教学实践中学生的分数计算和问题解决,关心学生成绩;一类基于心理学视角,关注儿童对于分数的认知加工和表征,考察学生对于分数的理解.以下重点探讨近15年来的知识演进脉络.
2.1 分数研究的近15年知识演进过程
纵观2006年后的研究工作,“数概念”成为关键词聚类的中心,表明认识分数概念的本质逐渐成为研究工作的立足点,分数中诸如“分数概念”“分数乘除法”等具体问题是多数研究绕不过的载体.研究主题围绕着“教”与“学”形成了两条研究主线.
2.1.1 围绕教学展开的研究
在“怎样教”的问题上经历了关注教学设计和具体教学问题;探讨整体教学结构;聚焦承载“教什么”和指导“怎么教”的教材比较研究3个阶段.探讨“怎样教”的过程中,研究者或从儿童分数概念学习的发展阶段及困难点出发[3],或基于当前分数教学模式,由学生分数除法、分数意义的理解层次[4–5],建构文章分析和测量框架,从学习结果出发展开研究,反观学习不足,提出具体改进建议.如,强调重视学生对分数及各部分概念和意义的深刻理解[6–7].或围绕分数教学中应“教什么”进行概念辨析,厘清分数概念的本质与内涵[8–10],提出“模式主导,双向多维”的分数意义的整体教学设计方案[11]和具体的教学实践改进策略.如,从度量模型引入分数单位[12],展开行动研究[13],推进研究者对于分数概念与教学的深入理解[14–15].
在聚焦“教什么”和“怎么教”的教材比较研究中,研究者就具体的分数内容对中、美及新加坡教材中定义类型、表征方式和编排顺序做了比较研究[16];在整体内容的编写依据、组织结构,以及教科书编写理念和呈现方式等方面的比较亦有涉及[17–18];中、日、新加坡,中、韩,以及中国大陆和中国台湾地区教材中例题和习题及分数除法内容编排的比较,横向上进行内容组织对比分析,纵向上对不同版本教材的难易程度,知识点呈现的认知深度,学生认知发展进行了研究[19–22].此外,研究者还透过不同的理论视角反观现有教材,提出编写建议[23–24].
2.1.2 围绕学习展开的研究
关于学生分数学习困难和学习认知的研究,最初延续关注学生分数学习结果,围绕学生分数学习困难的思路[25],反思学生在分数学习中对等分、单位量、等值分数等概念理解的发展阶段与实际困难,认为“整数偏向”是儿童学习分数的抑制因素,并探讨教学实施策略[26].随着研究的深入,对学生分数学习困难的研究视角逐渐由借助学生的分数学习结果反观学习困难,转变成考察学生分数学习具体问题,尝试从心理学角度解释学习困境.如,学生通过“部分—整体”模型习得分数概念后形成的误区及学习困难[27].
在分数认知方面,通过实证研究对儿童的分数概念认识、分数表征,以及认知加工方式等进行深入探讨.从关注个体学习出发,梳理了儿童建构分数概念时所采用的分割计数和相对量的知觉两种心理基础及建构机制,对分数概念语义理解水平和模式进行深入探讨[28–30];尝试从儿童思维发展水平和对等值分数语言认知两个方面,解释儿童在理解等值分数概念时的困难,将小学一~三年级儿童等值分数概念的发展划分为整体量概念、数量化的相对量概念、正式的等值分数概念3个阶段;设计并实施干预实验,提出尝试开展等值分数的早期教学,从小学低年级入手,在个体的非正式整体量基础上逐步推进对正式概念的学习;通过让儿童关注等值分数任务情境中各对应维度之间的乘法关系,能有效促进儿童乘法思维发展的具体教学建议[31–32].在分数表征与认知加工方式研究方面,聚焦儿童非符号材料上的分数表征方式[33–34]、分数数量表征的准确性及形式[35–36]、分数估计的表征模式[37]、分数表征转化能力[38]、整数数量表征与分数数量表征的关系[39]、在分数比较或解决分数应用题的认知加工方式等[40],通过被试的表达,对问题测量结果进行统计分析,得出儿童分数表征和分数认知的事实结果.其中,分数教学的宏观指导建议详见结果讨论部分.
2.2 分数研究的知识主线分离
值得注意的是,将学术研究者的研究工作分为“分数教学及分数学习”和“学生分数认知”两组,分析文献共被引发现,研究者仅在讨论小学数学中分数的多层级理解[10]及整体构建分数意义的教学行动研究[13],引用了学生分数概念认知的相关工作.另一边,仅一项五年级和六年级学生分数表征转化能力的调查研究[38]参考了已有分数教学问题的相关结果.这反映出,一方面,心理学研究工作关注学生分数认知的事实规律,却较少关注认知规律对教学活动的真实影响,这可能与心理学科研究者的科研工作多从学术角度出发,对实践关切不足有关.另一方面,教学研究关注的焦点在于知识层面的概念与内涵,忽视学生认知能力状态,多从“教师教”的角度,基于实践思维考察分数教学的相关主题,忽略学生自分数学习之始已将其先前经验(如幼儿早期对于非符号分数的计算能力、整数计算能力等)带入学习中的事实,对学生作为学习的积极参与者和知识的共同建构者在学习活动中的主体性关注不够.
从数学教育传统来看,可能是在教与学的统一活动中,普遍重视教多于重视学;基于“跟我学”思维逻辑展开学习指导与实践研究,是“我教你,你去学”,而不是“你去学,我适时、恰当地教”;漠视学生学习真正发生的过程,疏于反思教的本质是为了促进和帮助学生更好去学的事实.从中国教育的历史中考察,教学大致围绕着教师来发生是传统中国教育的一个十分重要的特色[41].传统教学中,通过会话或对话的方式来教学,一方面使因材施教得以实现,另一方面强化了教学方式中教师引导的重要地位.随着社会工业化的发展,传统的小组式学习和师生会话的教学方式面临着整班教学的挑战;规范的学科知识体系,细致明确的教学目标,定时定量完成的教学任务,冲击着教师因材施教的可能性.然而,教学围绕着“教”展开的认知却在撕裂了的师生双主体的传统教学形式中保存了下来,使得教师教与学生学的统一活动中,呈现出对“教师教”的思考多于对“学生学”的关注;教学内容依据教学计划展开,忽略学生学习的真实需求;教学方法依据教学内容选定,漠视学生学习真实发生过程.伴随着信息化时代的浪潮,关注每一个学生的学习再一次成为教学的方向和可能.因此,尝试从教学活动的另一面,“学生学”的视角探讨分数研究主题是未来研究的新动向.
3 分数研究的重要问题梳理与讨论
如前所述,通过对文献的系统分析,从教师、学生和分数教学内容,及3者相互联系的角度,立足于沟通教师与学生、学生学习与所学内容,尝试勾勒分数研究的知识脉络.对于研究者重点关注的分数概念的内涵,学生的分数认知、教材编排、分数教学等议题,以分数教材的编排与分数概念的引入为抓手,做进一步梳理和阐释,探讨基于“学生学”的教材编写和分数概念引入.
3.1 分数教材编排:分数的概念意义或学生的分数认知
3.1.1 分数的概念意义
在学生的分数学习研究中,研究者倾向从分数的意义出发探讨分数是什么而决定学生需要学什么.对于分数意义的研究多参考Kieren对于分数概念解读的5个方面:整体与部分的关系、比、商、测量与运算符(operators)[42],发展出对分数的不同解释.张奠宙先生用“份数”解释分数定义与除法的包含除、平均分的关系,强调“先将整体平均分成若干份”是等分除角度的定义,“部分占整体大小”是包含除模型[43].Kieren也认为,比的关系包含了“整体与部分关系”与“部分与部分关系”两种解释,提出分数“整体与部分关系”的解释是“比”的一种特殊情形,同时强调了两种思维方式在认知心理上的不同.也有研究者放弃整体与部分关系的含义,探讨分数作为比、商、测量和运算的4种解释方式[3,13].从数系扩张的角度看,用两个线段长度比表达分数,是用几何的方法解释无理数[44];分数纯数学上的定义,是指两个整数相除的商[3],即表示两个数关系的数.

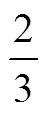
3.1.2 学生的分数认知
分数认知是数学认知研究的一个关键领域,从儿童认知角度来探讨其理解分数困难的形式和原因是近年来国内外分数研究关注的重要主题.其中,整数偏向(whole number bias)[46]是指学生趋于稳定使用有关整数的独立单元计数图式来解释分数的倾向,被认为在学生的分数认知中普遍存在,主要体现在比较分数大小、排序和分数的加减法运算上[27],它是否是儿童分数学习困难的影响因素? 中国研究者在这个问题上的研究,首先关注到教学实践中整数偏向对于学生分数学习的负面影响[47],梳理了整数偏向的可能成因,即学生在构建分数概念时新旧知识之间的干扰和数字认知的起源和发展的更普遍问题.其中与分数教学相关的因素是,教师在教授分数概念时从部分—整体引入,强调了整数概念,造成学生对分数测量含义的不理解,教授分数比较和运算时,用先前的整数策略使学生更快捷地习得解题方法,虽为学生从整数系统扩展到有理数系统提供了很好的桥梁作用,但也为整数偏向的出现提供了可能性[27].研究者测查55~75个月幼儿非符号的分数和整数计算能力发现,避开符号的干扰后,幼儿的分数计算能力尽管略低于整数计算能力,但远好于随机水平,且两者具有相似的发展模式[33],排除了整数偏向发生的认知起源和发展因素,将发生的可能因素聚焦在分数学习过程的影响上.进一步,通过对小学生在非符号材料上的分数表征方式的实证研究发现,放弃分数符号转用非符号性分数材料,排除了整数的影响时,被试可以很好地完成分数比较任务[34].这促使研究者反思,整数偏向或其它系统性的误解并不是影响学生学习分数的主要因素,不准确的类比才真正阻碍了学生的学习.并提出了在教学中密切联系幼儿的早期分数经验[33],考虑将分数教学提前,甚至可以和整数知识同时教授给学生的教学建议[28,34].
尽管国内研究者从儿童认知层面关注到整数偏向问题的时间较国外晚,但随着研究的不断深入,后续的工作进展与国际研究工作几乎同步.研究者基于Siegler等提出“分数和整数的理解之间具有关键的连续性”[48]的观点,进一步发现,儿童与成人在不同的数字线上的分数表征与整数表征结果非常类似,并认为分数作为一种数量符号是对整数符号的扩展[37];分数与整数的数字线任务的研究证实了五、六年级学生整数数字线估计对分数数字线估计的积极预测作用,说明整数数量的理解是分数理解的重要前提[39].上述研究不仅解释了整数的认知不会抑制分数的学习,相反,强调了分数的测量意义对于儿童理解分数和整数的联系和相似点的益处,为合理地安排学习内容,促进学生将整数的认知扩展到分数等其它类型数概念的理解提供了理论基础.
3.1.3 教材内容编排的研究述评
中国教学实践活动对教材依赖程度较高,教材的编排方式往往对教和学产生较大影响.研究者通过对不同国家及版本教材的对比分析,对分数教学内容编排提出指导性建议;通过关注分数内涵及其历史演变过程,聚焦分数知识本身在教学中的重要作用,从教育工作者期望达成的教学目标出发,围绕分数认知模型、任务设计、材料提供、习题选择、课时保证对教材内容进行编排.然而此类研究落脚点在教师的教学,而不是学生的学习,是知识本位视角的探讨.尽管有研究者关注到教学内容的编排应关照不同年龄段学生的认知特点,从认知复杂程度及认知深度出发对分数教学内容进行适切性调整,但是这样的研究从学生认知发展的一般规律出发,并没有真切地反应出学生在具体分数学习过程中产生学习困难的原因及心理因素.
促进学生学习发生是教材编写的核心任务,关注分数概念意义与学生分数认知是在“分数”内容和学生学习之间搭建桥梁的基础.教材编写从分数的意义出发,不能仅落脚于分数知识,需从学生分数学习出发关注儿童分数认知的真实状况.关于分数认知的研究中,学生的分数概念语义理解水平,对分数的认知和整数认知相互联系的关系;“部分—整体”认知模型带来的整数偏差;测量意义上分数概念理解的重要性;分数作为“数”的概念对于理解分数和分数运算的重要作用等,对于指导儿童的分数学习具有重要的意义.教材编写不能仅依赖“分数概念本质”这一知识本位的编写思路,更应关注学生分数学习的真实困境,考量分数认知发展的研究成果,区别作为学生学习的分数知识与分数知识本身之间的差异,体现教育研究对学生学习的真实关怀.
3.2 分数概念的引入:“切蛋糕/分桃子”模型或测量模型
3.2.1 分数概念引入教学的现状
考察已有98份“分数认识”相关文献,从涉及的人教版、北师版、苏教版教材的分数概念定义来看,人教版教材强调“将整体平均分为若干份”,分数是指“取其中一份或几份”,北师版和苏教版教材从单位“1”的角度对整体所表达的含义不仅包含“一个物体”,还包含“把多个物体看作一个整体”做了说明,从部分—整体的视角引入分数概念,更多关注到的是分数“作为整体的部分”的含义,淡化“整体”与“部分”的关系.基于文献中的教学实录、教学设计,教学片段反思可知,分数概念教学多采用区域模型(分割一个具体的圆等图形或实物)和离散物体模型(分一堆桃子等实物)为表征方式呈现学习活动,从“不能够用整数恰当表达一个数”的教学情境出发,引发学生认知冲突,借助“部分—整体”模型引入概念.教学反思时,教师关注具体情境中学生的学习过程对于促进数学思考的影响;探讨直观演示、操作活动对于提升学生数学活动经验及形成分数概念的教学效果.鲜有教师关注到学生的分数认知基础和认知结构,通过学生解决分数问题的方法对其思维过程进行合情推理.

3.2.2 分数概念构建机制
对于儿童来说,进入分数学习之前可能是带着关于分数的相对量大小的知觉,或分割(split)和迭代(iterate)的先前经验的.儿童在其发展早期,可能基于类比数量表征能力来笼统认识分数量的大小,而在发展后期,可以基于分割计数操作来实现对分数量大小更为精确的认识[28].从学生学习的角度考察其分数概念如何在个体先前经验基础上建构而成,能够从分数认知层面为更合理的引入分数概念,为优化分数教学提供心理学的理论基础.研究者在梳理了Tzur的反省抽象过程和Kieren的递归过程这两个分数概念的个体建构理论发现,Tzur借用了皮亚杰提出的反省抽象,并具体说明了个体如何从自身的分割动作之中抽象出分数概念的部分—总体含义,是分数概念建构的过程模型;而Kieren将分数概念的建构机制比喻为逻辑上的递归过程,侧重于强调分数概念建构的不同层次及层次间的同构关系,即高层次理解是对低层次理解的拓展,是分数概念建构的层次模型[28].

在分数概念层次理论上,研究者综合分析了Kieren的分数概念层次结构理论、Behr的分数概念语义结构论和Vergnaud的分数概念域理论,尝试依据3种理论试图解决的分数概念的多个含义关系和分数概念不同含义与分数运算任务之间关系为理论框架,探查儿童对于分数概念语义理解的水平[30,50].一个有趣的结果是,中国学生语义含义的理解水平上,学生理解和掌握水平最高的是商的含义而不是部分—整体含义,与理论之间存在一定的差异,也从侧面反映教学干预对于学生认知发展的影响.
3.2.3 从测量角度引入分数概念的可行性探索
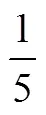
事实上,从分数知识的抽象程度来看,分割和形成分数单位是进行复合单位运算的基础,对分数单位的正确理解是进行分数概念学习、运算学习的关键和核心.而如何看待“分数单位”这一重要概念是“切蛋糕/分桃子”模型区别于测量模型的关键之处.换言之,“分数单位”是一个来自整体的部分的分数,还是独立于整体之外,和整体之间存在倍数关系的分数,是两种分数概念建构方式的冲突所在.基于学生分数认知发展特点,从学生数概念扩展的角度来看,建立分数单位概念基础将更有利于学生思维结构的发展,而将测量单位看作是分数概念的起点,能够较为合理地解释分数的起源以及用乘法推理思维解释分数的运算.
4 分数研究主题进一步探讨及启示
分数作为小学数学教学的重要内容,其典型性和代表性不言而喻,以上通过与学生分数学习紧密联系的教与学研究的立体考察,可清晰地看到研究者对“教师教”与“学生学”非二元对立的理解,以及分数作为学生学习的具体知识内容,为教师教与学生学的活动建立起自动联结的关注.以下进一步探讨与分析分数研究主题,为中国数学教与学的研究提供一个反思性的视角,也为数学教育研究工作提供些许经验和启示.
4.1 基于“学”的知识探讨是应然视角下内涵分析的有益补充
对于教学而言,“教什么”和“学什么”是构成教与学活动的核心基础之一,对分数本质认识的深入探讨是必要且重要的.然而,已有研究多是分数知识角度展开的应然探讨,较少见到对学生分数学习实然角度的关注.研究者不仅需要关注分数概念的部分—整体关系,比、商、测量、运算符等模型意义;从分数概念本质的角度厘清学生学习的分数知识具有怎样的结构和含义;处于小学阶段“数与代数”知识框架的何处,对于后续有理数学习有着怎样的基础意义;也需要探讨学生在自身分数概念建构中分数数感的建立、分数大小的理解;以及分数计算,特别是除法学习过程中,由于分数与整数、分数除法和整数除法相类似的概念结构,受到整数先验知识干扰导致的整数偏向对分数学习的影响.因而,从“学”的角度对于知识的探讨是应然视角下对知识内涵分析的有益补充.
4.2 关注学生学习的真实发生是改进教学实践活动的基础
关于分数内容“怎么教”,一直是学术研究者和教学实践者共同关注的议题.学术研究通过教学设计的整体架构和教材内容的编排研究对改进分数教学提供指导建议;教学实践则更多关注教学环节操作层面的改进.事实上,研究者在教学研究活动之前,已经对分数概念有了深刻理解,甚至形成了对分数理解的固有模型,作为知识的已知者,在进行教学设计时常着眼于如何将知识概念以符合教学一般规律的方式,逻辑清晰、条理分明地呈现出来.换言之,教给学生的是教师认为恰当、合适的数学,往往忽略了学生作为学习主体,其自身所具备的学习经验和概念基础,使得教师的教与学生的学沦为两个看似融合,实则独立的活动,教学实践改进难有本质突破.关注学生学习真实过程中的认知困难和学习困境,有针对性地开展教学实践或许是跨越“教”与“学”鸿沟的有效方式.因此,理解学生的数学认知不能仅仅是学术研究的议题,以学生数学认知研究结果与方法为基础,与教学实践中的具体困境相结合是改进教学实践的方向之一.
4.3 基于学生学习的评价是促进学生核心素养培养的风向标
在分数学习评价方面,研究者从学生分数学习结果出发,反思学生分数学习中学习困难,反观学生的分数认知状态,却较少有对学生分数学习过程监测、思维发展等议题的探讨.譬如,研究者关注到学生分数计算的准确性和流畅性,却忽略学生的计算能力来源于对计算程序性知识的熟练掌握,还是对分数运算概念的理解,抑或是两者相互支持的结果.研究者关注到学生在解决分数问题,特别是分数应用题中对分数单位概念的迷思,缺乏问题解决意识等现象,却鲜有关注分数问题解决背后学生数学思维的发展,忽略学生分数概念建构的认知理论和认知基础.换言之,在强调应让学生学会理解分数概念,学会分析问题和解决问题的同时,忽视了分数概念培养与学生数学思维发展相联系的契合点,如,单位分数概念的建立与乘法推理思维发展、分数计算与有理数计算的合理类比等.评价导向是当前教学实践活动的现实起点,基于学生学习过程的评价研究,实现学生学习评价过程和结果的统一是未来研究的重要议题.
4.4 教师的数学教学观研究是指导教学实践活动的前提和保障
在分数教学的研究中,一方面,职前和职后教师是否具备理解分数概念,解释错误分数模式的知识,理解学生在分数学习过程中特殊的认知过程,选取恰当的教学方式是研究者关注的重要议题.另一方面,教师应具备怎样的分数知识、分数教学知识,以及学生的分数学习知识以支持其在教学活动中做到尊重、理解学生关于分数的先前经验并指导学生的学习活动,也是关于分数研究的一个重要的、国内相关文献研究较少涉及的主题.此外,关于教师分数教学知识的研究中,研究者也注意到教师所具备的理论知识和实践经验的差距,其中典型的表现是,教师具备的分数教学知识与单调传统的教学实践行为的不一致.在教师具备丰富的学科教学知识对学生学习具有积极影响是教师教育领域的重要共识下,关注职后学习如何促进教师的学科教学知识和教学信念的发展,教师所具备的学科教学知识如何对数学课堂教学实践产生影响,是教师形成数学教学观的前提,也是教学实践活动顺利展开以促进学生的数学学习与素养提升的保障.
[1] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012:2.
[2] 郑毓信.小学数学教育的理论与实践——小学数学教学180例[M].上海:华东师范大学出版社,2017:82.
[3] 崔钰.关于分数的文献综述与教学实践[J].北京教育学院学报(自然科学版),2014,9(2):62–68.
[4] 巩子坤.理解视阈下的分数除法课程目标的实证研究[J].教育探索,2010(1):70–73.
[5] 范文贵,郝翡翠.五年级学生对分数意义的理解[J].数学教育学报,2017,26(1):70–75.
[6] 巩子坤,杨玉东.错误仅仅是粗心所致吗[J].上海教育科研,2007(9):90–93.
[7] 赵倩,吕世虎,韩继伟.中国大陆与台湾地区小学生数感表现的比较研究——以比较分数的相对大小为例[J].数学教育学报,2019,28(6):65–70,91.
[8] 张奠宙,唐彩斌.关于小学“数学本质”的对话[J].人民教育,2009(2):48–51.
[9] 章敏.关于分数教学的思考[J].课程·教材·教法,2015,35(3):63–67.
[10] 章勤琼,徐文彬.论小学数学中分数的多层级理解及其教学[J].课程·教材·教法,2016,36(3):43–49.
[11] 杨豫晖,宋乃庆.小学五年级“分数的意义”教学结构研究[J].课程·教材·教法,2010,30(4):54–57,78.
[12] 华应龙.分数:先分后数——“分数的意义”教学新路径[J].人民教育,2011(6):37–39.
[13] 张丹,孙京红.整体建构分数意义的教学行动研究[J].数学教育学报,2015,24(2):22–25.
[14] 刘加霞.通过“分”与“数(shǔ)”,分数是个“数(shù)”?——兼评华应龙老师执教的“分数的意义”[J].人民教育,2011(6):39–42.
[15] 李健,郑莹.分数概念的演变及其教学启示[J].内江师范学院学报,2018,33(12):30–35.
[16] 蒲淑萍.“中国美国新加坡”小学数学教材中的“分数定义”[J].数学教育学报,2013,22(4):21–24,70.
[17] 吴琼,高夯.美国、新加坡、中国小学数学教材编写的指导思想及其特点——基于教师用书的比较分析[J].外国教育研究,2013,40(9):120–129.
[18] 丁锐,YAN P X.中美小学数学教材的比较研究——以三年级“分数的认识”为例[J].数学教育学报,2016,25(3):20–28.
[19] 杨慧娟,郭蓉蓉,孟梦,等.中韩小学数学教材中分数除法的比较研究[J].数学教育学报,2020,29(2):64–69.
[20] 徐亚,隋佳源.小学数学教科书认知复杂程度的比较研究——以中国、日本、新加坡教材的分数问题为例[J].上海教育科研,2015(12):37–41.
[21] 张文宇,张守波.海峡两岸小学数学教材分数内容例题的比较研究[J].数学教育学报,2015,24(3):68–72.
[22] 张平,彭亮,徐文彬.大陆与台湾小学数学教材中分数除法的编排比较[J].数学教育学报,2018,27(6):38–43.
[23] 王光明,李健,康玥媛.小学数学教材中分数意义的呈现:历史顺序与“超回归”倒序的统一[J].课程·教材·教法,2017,37(5):34–39.
[24] 陈蓓,章飞.分数意义建构的顺序及对教科书设计的建议[J].数学教育学报,2018,27(4):58–61.
[25] 苏洪雨.七年级学生分数学习情况的调查研究[J].数学教育学报,2007,16(4):48–51.
[26] 杨伊生,刘儒德.儿童分数概念发展研究综述[J].内蒙古师范大学学报(教育科学版),2008(6):130–134.
[27] 刘春晖,辛自强.分数认知的“整数偏向”研究:理论与方法[J].心理科学进展,2010,18(1):65–74.
[28] 张睆,辛自强.分数概念的个体建构——起点与机制及影响因素[J].数学教育学报,2013,22(1):27–32.
[29] 张睆,辛自强,陈英和,等.分数概念语义理解对儿童乘法应用题表征的影响[J].数学教育学报,2017,26(4):76–79.
[30] 张睆,辛自强,陈英和,等.小学儿童分数概念语义理解水平及模式:基于潜在类别分析[J].数学教育学报,2018,27(3):66–71,75.
[31] 韩玉蕾,辛自强,胡清芬.等值分数概念的理解[J].心理发展与教育,2012,28(2):210–217.
[32] 辛自强,韩玉蕾.小学低年级儿童的等值分数概念发展及干预[J].心理学报,2014,46(6):791–806.
[33] 辛自强,刘国芳.非符号分数与整数计算能力的发展及其与数字记忆的关系[J].心理科学,2011,34(3):520–526.
[34] 辛自强,李丹.小学生在非符号材料上的分数表征方式[J].心理科学,2013,36(2):364–371.
[35] 孙玉,司继伟,黄碧娟.分数的数量表征[J].心理科学进展,2016,24(8):1 207–1 216.
[36] 高瑞彦,牛美心,杨涛,等.四~八年级学生分数数量表征的准确性及形式[J].心理发展与教育,2018,34(4):443–452.
[37] 卢淳,郭红力,司继伟,等.不同数字线下儿童与成人分数估计的表征模式[J].心理发展与教育,2014,30(5):449–456.
[38] 郭萌,熊妍茜,杨新荣,等.五年级和六年级学生分数表征转化能力的调查研究[J].数学教育学报,2016,25(5):49–54.
[39] 张丽,卢彩芳,杨新荣.三~六年级儿童整数数量表征与分数数量表征的关系[J].心理发展与教育,2014,30(1):1–8.
[40] 高婷,刘儒德,刘颖,等.小学生分数比较中的加工模式:基于反应时和口语报告的研究[J].心理发展与教育,2016,32(4):463–470.
[41] 李弘祺.学以为己:传统中国的教育[M].上海:华东师范大学出版社,2017:605.
[42] KIEREN T E. The rational number construct——Its elements and mechanisms [M] // KIEREN T E. Recent research on number learning. Washington DC: ERIC Publications, 1980: 125–149.
[43] 张奠宙,巩子坤,任敏龙,等.小学数学教材中的大道理——核心概念的理解与呈现[M].上海:上海教育出版社,2018:104–106.
[44] 娜仁格日乐,史宁中.度量单位的本质及小学数学教学[J].数学教育学报,2018,27(6):13–16.
[45] 倪玉菁.五、六年级小学生对分数的意义和性质的理解[J].心理发展与教育,1999,15(4):26–30.
[46] NI Y, ZHOU Y D. Teaching and learning fraction and rational numbers: The origins and implications of whole number bias [J]. Educational Psychologist, 2005, 40 (1): 27–52.
[47] 刘春晖,辛自强.五~八年级学生分数概念的发展[J].数学教育学报,2010,19(5):59–63.
[48] SIEGLER R S, THOMPSON C A, SCHNEIDER M. An integrated theory of whole number and fractions development [J]. Cognitive Psychology, 2011, 62 (4): 273–296.
[49] STEFFE L P. A new hypothesis concerning children’s fractional knowledge [J]. The Journal of Mathematical Behavior, 2001, 20 (3): 267–307.
[50] 辛自强,张睆.儿童的分数概念理解的结构及其测量[J].心理研究,2012,5(1):13–20.
[51] SIMON M A, PLACA N, AVITZUR A, et al. Promoting a concept of fraction-as-measure: A study of the learning through activity research program [J]. The Journal of Mathematical Behavior, 2018 (52): 122–133.
[52] STAFYLIDOU S, VOSNIADOU S. The development of students’ understanding of the numerical value of fractions [J]. Learning and Instruction, 2004, 14 (5): 503–518.
Teaching and Learning Fractions in Chinese Elementary: A Review of Literature in the Past 30 Years
HUANG Xiao-lin, HUANG Qin-an
(School of Mathematics and Statistics, Shaanxi Normal University, Shaanxi Xi’an 710119, China)
Based on a systemic review of papers involving fractions, there are two main lines of study around the questions of teaching and learning primary school fractions. One focuses on fractions as knowledge and the other pays more attention to knowledge of the cognition around fractions. These lines occasionally intersect, reflecting the effects of traditional education in China—by which teaching and learning activities revolve around teachers—on the study of mathematics teaching. From the perspective of the teaching and learning of fractions, we attempted to explore the feasibility of teaching materials compiled on students’ cognition of fractions and the method of introducing the concept of fractions using the measurement model to show that the concern of education research to students’ learning. We put forward the following viewpoints: based on “learning,” explore mathematical knowledge to enrich knowledge connotation; pay attention to the process of student learning to improve teaching practices; deepen mathematics learning evaluation to promote the cultivation of students’ core literacy; strengthen teachers’ mathematics teaching views to guide their teaching practices; and provide references for mathematics education studies.
the concept of fractions; teaching and learning of fractions; teaching material compiling; measurement model
G622.0
A
1004–9894(2021)06–0039–07
黄晓林,黄秦安.中国三十年来小学阶段分数研究文献的系统分析及启示[J].数学教育学报,2021,30(6):39-45.
2021–08–10
国家哲学社会科学基金2017年度教育学重点招标项目——教师核心素养和能力建设研究(AFA170008);中央高校基本科研业务费专项资金资助——基于乘法推理教学的小学数学教师数学教育观念系统研究(2019TS091)
黄晓林(1984—),女,安徽定远人,博士生,主要从事数学教育与数学教师教育研究.
[责任编校:周学智、陈汉君]
