硝酸熔盐纳米流体比热容提高的模拟与实验研究

魏小兰 林国庆 丁静 王维龙 陆建峰 刘书乐

(1.华南理工大学 化学与化工学院，广东 广州 510640；2.中山大学 材料与工程学院，广东 广州 510006)

新型清洁无污染能源的高效应用是应对能源危机和环境污染的有效措施。太阳能作为一种可再生清洁能源，具有极高的利用潜力[1- 3]。太阳能光热技术能够整合储热系统，使其成为包括我国在内的众多国家和地区利用太阳能发电的重要选择[4- 10]。为摆脱太阳能利用中的季节局限性，解决发用电高峰的不匹配问题，工程上需要一种能够将太阳能储存起来以待调配供给的储热材料。为了最大化能量利用率，目前多使用温域宽、蒸气压低、热导率和比热容均较大的熔盐作为传储热材料。

传储热系统中储热材料的性质决定了整个系统的效率[11]，目前商用比较成熟的熔盐多为硝酸熔盐(如太阳盐、Hitec等)，但是硝酸熔盐的明显缺点是热物性(尤其是比热容)相对较低。为进一步强化传储热工质的热物性，提高传储热效率，Choi等[12]首次提出向流体里加入极少量纳米颗粒形成纳米流体，并发现该方法能使流体的热性能有明显提高。近年来，越来越多的学者对各种纳米流体进行了研究。Shin及其团队[13- 14]在Li2CO3-K2CO3熔盐中添加1%(质量分数，下同)的SiO2，流体比热容提高了19%～24%；在三元LiNO3-NaNO3-KNO3中掺杂SiO2(粒径分别为5、10、30和 60 nm)，流体比热容增幅在13%～16%之间。Jo等[15]在二元Li2CO3-K2CO3熔盐中复合碳纳米管(MWCNT)，通过改变熔盐配比发现，无论固态还是液态，混合物的比热容都有明显的提高，液态流体比热容提高可达6.0%～29.3%；Ding及其团队[16- 19]用球磨法在太阳盐中添加CuO和TiO2，CuO添加量最低(0.1%)时比热容增幅最大(提高10.48%)，添加量升高到1.5%时比热容开始降低，而添加TiO2的流体的比热容增幅与TiO2添加量无关；Wen及其团队[20- 24]发现：在太阳盐中掺杂0～2.0%的Al2O3，流体比热容提高了1.9%～8.3%；利用CuO2O4·0.5H2O原位生成(0.1%～3.0%)CuO纳米流体，CuO含量为0.5%时，太阳盐熔盐的比热容增幅达11.5%。以上针对不同制备方法和体系的研究结果都说明，纳米颗粒的加入会明显提高熔盐流体的比热容。

然而，纳米粒子对比热容的改善不符合混合模型[25]的预测，由此引发了人们对加入纳米颗粒后比热容提高原因的探讨，例如以下猜测及模拟研究：Ho等[26]用所开发的新型装置复合Al2O3与Hitec熔盐，发现添加量在0.063%时比热容提高率达19.9%，而在添加量大于2.000%时比热容会下降，为探究其原因，他们建立了界面区域简化模型，认为纳米颗粒是通过提高其界面面积来提高熔盐比热容的；Seo等[27]观察到，加入纳米颗粒后熔盐流体会在纳米颗粒表面形成树突状结构，并认为这种树突状结构是比热容增加的原因；Qiao等[19，28]和Jo等[29]通过分子动力学分别研究了SiO2在NaNO3中分散、SiO2在KCl中分散、石墨在Li2CO3-K2CO3中分散的效果，一致认为熔盐在纳米颗粒周围会形成密度增大的压缩层，这种压缩层的存在造成了比热容的提高。

目前的模拟研究存在以下不足：1)所构建的纳米熔盐体系包含的原子数量有限，仅容纳了1颗粒纳米粒子且粒径仅为1 nm，而且被放入的粒子多为实心球体，没有考虑纳米粒子自身的原子空间结构，因此无法揭示熔盐与纳米粒子之间的界面效应本质；2)在计算纳米粒子添加量对比热容的影响方面，现有模拟只能通过减少熔盐的原子数量来改变颗粒与熔盐的相对含量，无法说明实际纳米熔盐流体中多纳米颗粒以及由此产生的粒子团聚现象对纳米熔盐流体比热容的影响，导致模拟结果不理想；3)现有模拟计算多关注纳米粒子加入后对纳米熔盐体系整体热物性的影响，较少关注纳米颗粒的加入是否会导致熔盐流体内阴阳离子微观结构的变化，因此忽视了熔盐微观结构变化对纳米熔盐流体热物性改变的贡献。事实上，深刻认识这些影响对指导纳米熔盐流体的制备、保证纳米熔盐流体的高效运行至关重要。为解决上述问题，文中构建了原子数量更大的模拟体系，同时构建了原子有序排列的SiO2晶格模型，以研究不同数量纳米粒子对熔盐微观结构的影响，以及熔盐在不同纳米粒子表面的分布状态；在此基础上，研究纳米粒子的分散程度对熔盐热物性的影响，并对纳米粒子添加量对体系内各种形式能量的影响进行拆解研究，以期揭示纳米粒子引起纳米熔盐流体比热容提高的微观本质。

1 方法与步骤

1.1 模拟方法

采用分子动力学方法，从微观尺度模拟在二元太阳盐熔盐中加入不同含量及粒径的SiO2纳米颗粒后，熔盐流体的热物性及微观结构。

1.1.1 力场

对于硝酸熔盐以及纳米颗粒的分子动力学模拟，非键相互作用部分选择了带有库仑相互作用的Buckingham势，以获得更为准确的硝酸盐的微观结构，即

(1)

式中：等号右边第1项描述离子间斥力，Aij为斥力参数，ρij为硬化参数，rij为两原子间距离；第2项描述偶极色散作用，Cij为范德华色散力参数；第3项描述离子间库仑力，qi、qj为离子所带电荷；E为Buckingham势总能量。

对于成键部分，比较了Jayaraman等[30]和Ni等[31]的工作后发现，后者在规定键角弯曲时采用的Uray-Bradley项能更好地描述硝酸根的微观结构，对于物性模拟的结果更加准确，因此采用后者进行文中研究，其成键相互作用表达式为

E=Kb(r-r0)2+Ka(θ-θ0)2+Kub(r-rub)2

(2)

式中，等号右边第1项表示N—O键的拉伸振动，第2项表示O—N—O的键角弯曲，第3项表示O—N—O角中两个O的非键相互作用(距离)。式中具体符号的物理意义见文献[31]，文中不再赘述。成键相互作用部分分子动力学模拟的力场参数分别是：Kb，169 025 kJ/(mol·nm2)；r0，0.126 76 nm；Ka，261 458.2 J/mol；θ0，120°；Kub，478 231.2 J/mol；rub，0.219 55 nm。

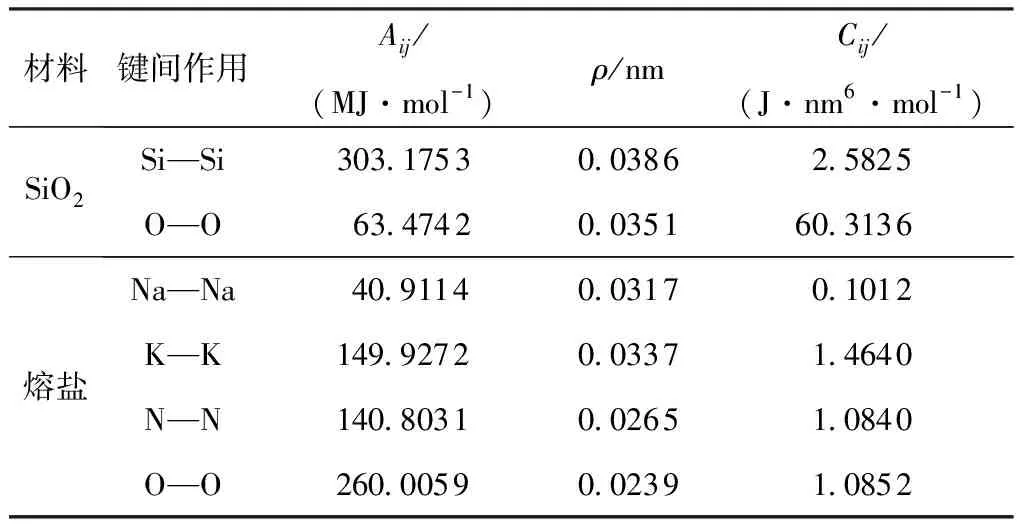
表1 非成键相互作用部分分子动力学模拟的力场参数

1.1.2 模拟细节

文中使用的模拟软件为分子动力学软件LAMMPS，计算平台为“天河二号”计算机系统。为了避免粒子丢失和消除边界效应，采用周期性边界条件，截断半径小于模拟盒子边长的一半，截断半径之外的长程库伦相互作用使用PPPM方法计算，以减小计算误差。

如表2所示，在计算之前，对单元熔盐与SiO2颗粒进行了单独的模拟，得到与实验值吻合较好的密度结果，确认了计算的可靠性。为了模拟纳米粒子分布在熔盐中相对更加真实的情况，不同于Jo等[29]模拟的初始结构，文中在添加不同含量的粒子时，固定二元熔盐的总原子个数(7 840)和初始模拟盒子体积不变，往其中加入直径为1 nm的SiO2纳米颗粒，通过改变SiO2颗粒的加入数目来改变总质量分数。图1(a)和1(b)分别为加入1个和2个纳米颗粒后的初始模型。在考察SiO2粒径的影响时，则先将粒径分别为1 nm、2 nm的SiO2纳米颗粒放在模拟盒子中心，使熔盐离子随机分布在其周围，在密度一定时通过改变模拟盒子的体积来控制离子的加入量。在考察不同熔盐离子与纳米颗粒距离下熔盐离子的分布情况时，将纳米颗粒之外的熔盐部分以球形纳米颗粒球心为共同球心，分割成半径逐步增大的若干个同心球壳，如图2所示，计算每一个球壳中的粒子浓度，即得到粒子密度随距离变化的情况。

表2 NaNO3、KNO3和SiO2密度的实验值与模拟值比较

(a)SiO2添加量为0.5%时

(b)SiO2添加量为1.0%时

图1 模拟中的初始模型

初始模型建成后，首先经过一个能量最小化的步骤以防止原子之间出现重叠，之后将系统温度升高到1 000 K以确保熔盐完全熔化，再模拟退火降温到目标温度，在NPT系综下使用Nose-Hoover方法控制温度和压力，确保体系弛豫足够长时间以达到平衡。分析弛豫后系统的动能、势能及其拆分的分子内的能量、库仑能、长程作用力的能量等的变化，然后通过能量、焓的变化得到整个系统的比热容，并使用MSSP程序计算得到径向分布曲线。

图2 纳米球团外熔盐分层示意图

1.2 实验方法

为研究纳米粒子添加量对熔盐比热容的实际影响，制备了相应的纳米熔盐，并测试所制纳米熔盐复合液体的比热容。

1.2.1 材料制备

文中用到的NaNO3、KNO3均由广州化学试剂厂提供，纯度为99.5%；20 nm SiO2由南京先丰纳米材料科技有限公司提供，纯度为99%。将NaNO3、KNO3置于120 ℃烘箱中干燥24 h，除去水分后按照太阳盐比例分别称取所需质量的组分，随后放入坩埚中机械混合均匀，采用静态熔融法在350 ℃马弗炉中恒温加热3～4 h，使熔盐完全处于液体状态并混合均匀形成共晶熔盐，冷却后将其研磨成粉末并置于干燥器中密封保存。按照SiO2的各个质量分数，每次称取精确质量的20 nm SiO2纳米粉末，通过静态搅拌法将SiO2粉末加入到二元硝酸熔盐中，350 ℃下保温3 h使其完全混合，自然冷却至室温后密封保存。

1.2.2 比热容测量

采用DSC差示扫描量热仪[32]测量熔盐比热容，用已知比热容的蓝宝石当做基准物。用铝锅作为测量容器，先后3次测定DSC曲线。第1条DSC曲线为空坩埚时的热流曲线，即基线；第2次测定蓝宝石升温时的曲线，即标准线；第3次测定样品的热流曲线。以这3条热流曲线为基础，根据式(3)计算样品的比热容：

(3)

在式(3)中：cp，sample和cp，sapphire分别为样品和蓝宝石的比热容；Qsample、Qblank和Qsapphire分别为待测样品、空坩埚、蓝宝石的热流；msapphire、msample分别为蓝宝石和样品的质量，为了减小误差和保证测试的可重复性，一般将样品质量称取得与蓝宝石质量接近。装样品时尽量使样品铺满铝坩埚底层表面以避免样品融化时溢出。测量过程在氮气环境下进行，气体流速为80 mL/min，升温速率为10 ℃/min，先由室温升高至90 ℃，恒温10 min以除去水分并保持信号稳定，再由90 ℃程序升温到400 ℃，恒温5 min，然后冷却至室温。

2 结果与讨论

2.1 纳米熔盐复合流体的比热容cp的变化

比热容cp的计算方法有两种，第1种是通过系综平均得到的能量涨落计算得到，如式(4)：

(4)

式中：〈δE2〉=〈E2〉-〈E〉2，E为体系的总能量；kB为玻尔兹曼常数。第2种是通过定压焓变ΔH来确定，如式(5)：

(5)

文中比较了两种方法得到的结果后，采用了更接近实际的第2种方法来计算比热容。

考虑到计算量和计算周期，选择1 nm SiO2加入KNO3-NaNO3二元硝酸熔盐中形成复合液体，计算不同纳米粒子添加量下复合液体的比热容，探讨复合液体比热容增大的可能性。与现有研究仅添加1个纳米颗粒并通过降低熔盐原子数来改变SiO2添加量的方法[18- 20]不同，这里采取与实际情况更为接近的增加纳米球团个数并调整熔盐原子数的方式来改变纳米熔盐复合液体的相对含量。

在实验制备过程中，发现粒径小于15 nm的SiO2粉末由于粒径太小其表面润湿性较差，难以按预期含量制备出理想的、混合均匀的纳米熔盐复合液体，于是采用粒径为20 nm的SiO2进行制备，以测量纳米熔盐复合液体比热容的提高情况。图3分别给出了含1 nm和20 nm SiO2的纳米熔盐复合液体比热容的模拟值与实验值。从图3可知，随着复合液体中SiO2纳米颗粒含量的增大，纳米熔盐复合液体比热容的测量值和模拟值大体上都呈现先增大后增幅减缓的趋势，即实验和模拟中都存在着一个最佳的添加量。在模拟中，SiO2添加量在1.0%～1.5%时比热容提高最多，相比基础熔盐提高了约7.6%。加入纳米颗粒的熔盐液体，其实测比热容的提高率比模拟结果小，这可能与实际纳米粉体中存在较大颗粒有关，也可能与实际纳米粉体添加量增大后在熔盐中发生聚集有关，还可能是由于硝酸熔盐与SiO2在工况温度下发生缓慢放热反应，使实测纳米流体热流曲线包含SiO2与硝酸熔盐的少量反应热，导致比热容测量结果较低。检索文献发现，Wei等[33]在石英(SiO2)坩埚中加热二元硝酸熔盐时，监测到了NOx的排放，并从化学热力学理论计算证明，硝酸熔盐在工况温度下可以与SiO2发生反应。

图3 模拟(1 nm)与实验(20 nm)中硝酸熔盐纳米流体比热容随SiO2添加量的变化

为探讨纳米熔盐复合液体比热容提高的机理，下面从纳米粒子对熔盐微观结构的影响、熔盐离子在纳米颗粒表面的分布特征、纳米颗粒分散程度与比热容提高相关性的角度，探讨纳米熔盐复合液体比热容提高的微观本质，通过对纳米熔盐复合液体内部各种能量分布的拆解，探析微观结构变化对宏观热物性影响的科学本质。

2.2 纳米颗粒对熔盐微观结构的影响

(a)K—O径向分布函数

(b)K—N径向分布函数

(c)Na—O径向分布函数

(d)Na—N径向分布函数

2.3 熔盐离子在纳米颗粒表面的分布特征

(a)SiO2粒径为1nm时

(b)SiO2粒径为2nm时

2.4 纳米颗粒分散程度对比热容增加的影响

为深刻认识纳米熔盐复合液体中纳米粒子分散程度对熔盐比热容提高的影响，选取粒径为1 nm的SiO2颗粒，与文献[18- 20]方法不同，在基础熔盐中加入多个纳米粒子使复合液体中的纳米粒子含量分别达到2.5%和3.5%(图6所示为2.5% SiO2添加量时聚集和分散情况下的初始模型)，以模拟实际纳米熔盐复合液体的多粒子状况，然后计算相同含量下纳米颗粒分散与聚集时各自的比热容，并加以对比，研究纳米颗粒分散程度对比热容的影响。这里采取的分散标准是：任意两颗粒中心的距离大于2 nm；聚集标准则是：颗粒在熔盐盒子中心组成一个大的球团。图7给出了不同纳米粒子含量下复合液体在分散和聚集状态下的比热容。结果表明，SiO2添加量为2.5%时，分散分布的SiO2颗粒加入后，复合液体的比热容为1.64 J/(g·K)，比相同添加量下聚集分布时的比热容高7.2%，比基础熔盐的比热容高9.3%。聚集分布的复合液体的比热容比基础熔盐的比热容仅提高2.1%，这与图3中实验测定的纳米熔盐流体比热容提高率小于预期值的结果相类似，在一定程度上说明，图3所示纳米熔盐比热容测量值规律性欠佳可能是由于纳米粒子的随机聚集所致。

(a)聚集

(b)分散

图7 添加2.5%和3.5% SiO2时聚集和分散情况下的比热容

2.5 纳米熔盐流体比热容提高机理(能量)分析

为了进一步说明比热容提高的本质，对不同含量1 nm SiO2熔盐复合液体体系在625 K时的能量组成进行拆解分析。如图8(图中曲线已按照绘图顺序编号)，整体的总能量(线1)包括动能(线2)和势能(线3)，其中势能包括范德华能(线4)、库仑能(线5)、分子内键振动扭曲的能量(线6)以及长程作用力的部分(线7)。

ET=EK+EP

(6)

EP=Evdwl+Ecoul+Emol+Elong

(7)

以上对对体系能量的分析式中：ET为体系的总能量；EK为体系的动能；EP为体系的势能；Evdwl为范德华力引起的能量变化；Ecoul为库伦能；Emol为分子内的相互作用力产生的能量，在文中具体表现为硝酸根N—O键的伸缩振动、O—N—O键角的扭转动，以及硝酸根的二面角和非正常二面角的扭曲振动；Elong为模中的截断半径之外部分的库伦力和范德华相互作用等投射到k空间的能量影响。

图8 模拟体系能量拆分

3 结论

(1)实验和分子动力学模拟计算结果表明，随着SiO2的加入，熔盐流体的比热容增幅先增大后减小，存在一个最佳的SiO2添加量。

(2)在微观结构模拟中，硝酸熔盐及其与SiO2复合的纳米流体呈现出短程有序、长程无序的特点。对于熔盐，纳米颗粒的加入会减小整体熔盐的阴阳离子Na—N、Na—O、K—N、K—O间的距离，且阴阳离子间距离越近，比热容提高得越多。

(4)纳米颗粒的加入使得阴阳离子间的距离减小，固液界面的定向排列压缩层的出现使得体系的库伦能增大，离子为克服库仑力需要更多的能量，从而在加热时表现为比热容增大，同时比热容的变化也与计算的截断半径之外粒子间的能量变化有关。

(5)SiO2添加量为2.5%和3.5%时，分散和聚集状态下的比热容数据显示，分散程度更高的纳米流体的比热容比聚集时的比热容增幅均有大的提高，这说明高的分散程度能有效提高比热容。上述研究从计算的角度初步证明：加入的纳米颗粒粒径越小、分散程度越高，制备得到的熔盐纳米流体的比热容提高就越大，这对高性能储热材料的研制具有一定的指导意义。