基于牛顿迭代法求解群速度的地震波射线追踪模拟

张定文,李卫东,段金龙,张学海

(1.河南工业大学信息科学与工程学院,河南 郑州 450001;2.应急管理部国家自然灾害防治研究院,北京 100085)

0 引言

研究表明,各向异性在地下介质中是普遍存在的[1-2]。传统的地下构造研究多是在各向同性或完全弹性的介质中进行,忽略了由各向异性导致的群速度计算误差而无法真实表达地下构造。随着计算机技术,射线追踪技术等发展,基于复杂各向异性地质模型的地下构造研究成为热点[3-7]。

地震波射线追踪作为一种快速有效的地震波场数值模拟方法,能够直观展现地震波的几何传播路径,清晰表达地下内部构造不均匀性以及速度结构各向异性,因此广泛应用于地震正演模拟,层析成像,偏移成像等领域。目前地震波射线追踪方法众多,主流的有两点射线追踪法、最短路径法、有限差分法、走时插值法和波前构建法等方法[8-9]。其中,最短路径射线追踪法最早由Nakanishi等[10]在1986年引入到地震波走时及射线路径计算领域,之后国内外学者相继对算法进行改进和系统化[11-15]。通过对地震波进行射线追踪模拟,可以获取地下速度结构物性信息,获取地下介质中地震波走时分布,实现对地下介质各向异性的直观表达,有效解读地质结构。

在地震波的走时计算和射线追踪模拟中,前人多是针对弱各向异性介质采用群速度近似的表示方法来进行计算[16-19],但当各向异性强度较大时,这些方法会造成很大误差。为此,本文拟对群速度计算公式进行推导,并利用牛顿迭代法快速求解群速度,以有效进行地震波在复杂三维地质中的射线追踪模拟。

1 群速度的计算

在各向异性介质中,由于群速度和相速度发生分离,波前面不再是以震源为中心的标准球形[20]。在已知弹性参数的横向各向同性介质中,P波相速度与相角θ的关系式如下:

(1)

式中:ρ是介质的密度;Cij(i,j=1,2,3,4,5,6)是介质的弹性参数;D(θ)的表达式如下:

D2(θ)=(C33-C44)2+2[2(C13+C44)2-

(C33-C44)(C11+C33-2C44)]sin2θ+

[(C11+C33-2C44)2-4(C13+C44)2]sin4θ

(2)

射角Ø和相角θ的关系如下:

Ø=Ø(θ)=θ+f(θ)

(3)

(4)

其中

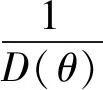
C33-2C44)]sinθcosθ+[(C11+C33-

2C44)2-4(C13+C44)2]sin3θcosθ}

(5)

群速度关于相速度的表达式为:

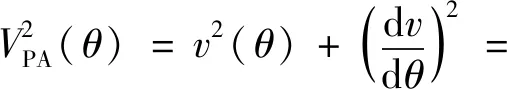
[v(θ)secf(θ)]2

(6)

牛顿迭代法是一种在实数域和复数域上近似求解方程的方法,通过切线来逼近零点,收敛速度很快。根据牛顿迭代法基本原理,在VP(θ)、ρ、Cij(i,j=1,2,3,4,5,6)已知的情况下,对式(1)和式(2)进行联立变形得:

g(θ)=4A1sin3θcosθ+2A2sinθcosθ

(7)

式中Ai(i=1,2,3)为常数,由VP(θ)、ρ、Cij(i,j=1,2,3,4,5,6)确定。

结合牛顿迭代公式可得式(8),根据式(8)可快速求出相角θ的精确近似值,从而得到群速度。

(8)

2 射线追踪

由于最短路径法计算效率快,且在网格密度十分密集的情况下,最短路径法得到的射线路径可近似为真实的理论路径,因此本文在牛顿迭代法求解群速度的基础上,通过最短路径法来实现地震波的射线追踪模拟。基于地层的起伏情况,采用Delaunay三角剖分法对三维地质结构进行剖分,其单元结构为不规则四面体。这样的不规则四面体结构不仅能够更加真实的展现地质结构,如突起、凹陷、裂缝等,还能方便地考虑各向异性的特点。

2.1 质点设置

三维地质速度结构模型中每一个四面体单元可以看作为一个质点,在这个单元体中各物性参数,各向异性强度可视为常数,即在该单元体内波速值大小一定。质点的位置位于四面体的中心,其计算公式如下:

x=(x1+x2+x3+x4)/4

(9)

y=(y1+y2+y3+y4)/4

(10)

z=(z1+z2+z3+z4)/4

(11)

式中(x,y,z)为质点坐标,(xi,yi,zi)i=(1,2,3,4)为四面体的四个顶点坐标。

每个质点的波速采用反距离加权法进行求解。反距离加权法是一种应用较广泛的加权平均插值法,在四面体的四个顶点中,距离质点较近的顶点波速所占权重较大,距离质点较远的顶点波速所占的权重较小。根据式(12)可求出质点的波速。

v=w1v1+w2v2+w3v3+w4v4

(12)

wi=di/D

(13)

式中:v为质点速度;vi为四面体四个顶点的速度值;wi为各顶点所占的权重;di为各顶点到质点的距离;D为四个顶点到质点的距离之和。

2.2 算法原理

最短路径算法实际上是一种局部寻找最优解法的贪心算法。地震波从震源点出发,先考虑与之相邻的点,在这些节点中选出走时最少的一点作为子震源,波会继续传向与子震源相邻的节点,在这些节点中再选出下一个子震源。按照这样的思路,重复循环就可以快速求出各个节点的走时。在进行射线路径的追踪时,从接收点开始依次寻找上一级震源直到震源点,记录所经过的节点就可得到射线追踪轨迹。具体步骤如下:

(1)初始化两个集合N和V。其中集合N保存所有质点中未访问过的质点,集合V记录已经访问过的质点。

(2)从震源点开始,寻找与其相连通且未被访问过的质点,将这些质点存入集合N中。

(3)在N中找出从震源点到该质点走时最小的点,将该点视为子震源点,存入集合V中,并找出该点的所有子震源点。

(4)遍历访问子震源点的所有子质点,并求出从起始震源点到这些子质点的走时,把这些子质点存入集合N中。

(5)循环步骤(3)和步骤(4),直到集合N为空。

在最短路径的循环遍历中,需不断选取走时最小的点,这就需要花费时间,导致算法运行时间较长。对于本研究数据为无序序列,可采取快速排序算法,从而提高算法的效率,节省算法运行时间。

3 实例应用

本文选取的研究区为华北克拉通山西断陷带北部局部区域,数据引自华北地区地壳-上地幔地震波速度结构模型v2.0,以P波波速进行群速度的计算和射线追踪模拟。华北克拉通是地球上最古老的克拉通之一,由于复杂的地质结构,导致该地区地质活动频繁,长期的地质演化、应力作用、板块运动及应变等都会导致该地区地下速度结构不均匀分布,从而该地区的三维速度结构中留存着长期的地质构造演化的信息[21]。因此,研究该强震区的地质结构具有十分重要的意义。

图1中红色矩形框内为研究区域,范围112°～113°E,40°～42°N,数据的分辨率在深度7 km以内为0.2°×0.2°×0.2 km;深度为7～50 km时为0.2°×0.2°×1 km。

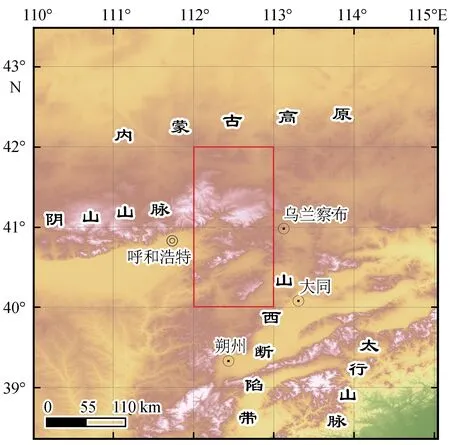
图1 研究区范围Fig.1 Study area

基于Paraview平台,利用其提供的开源脚本,使用Python语言进行脚本开发,进行该研究区三维地质模型的构建。若原始数据中已有投影坐标,则可直接读取投影坐标进行模型的构建;若无投影坐标,则需先导入Proj4投影坐标库,编写投影坐标函数,将地理坐标转为投影坐标。

对处理过的数据分别使用vtkDelaunay2D()类和vtkDelaunay3D()类进行二维地层速度界面和三维速度结构模型的构建,并将二维地层速度界面和三维速度结构模型相结合,得到三维地壳速度结构模型(图2)。

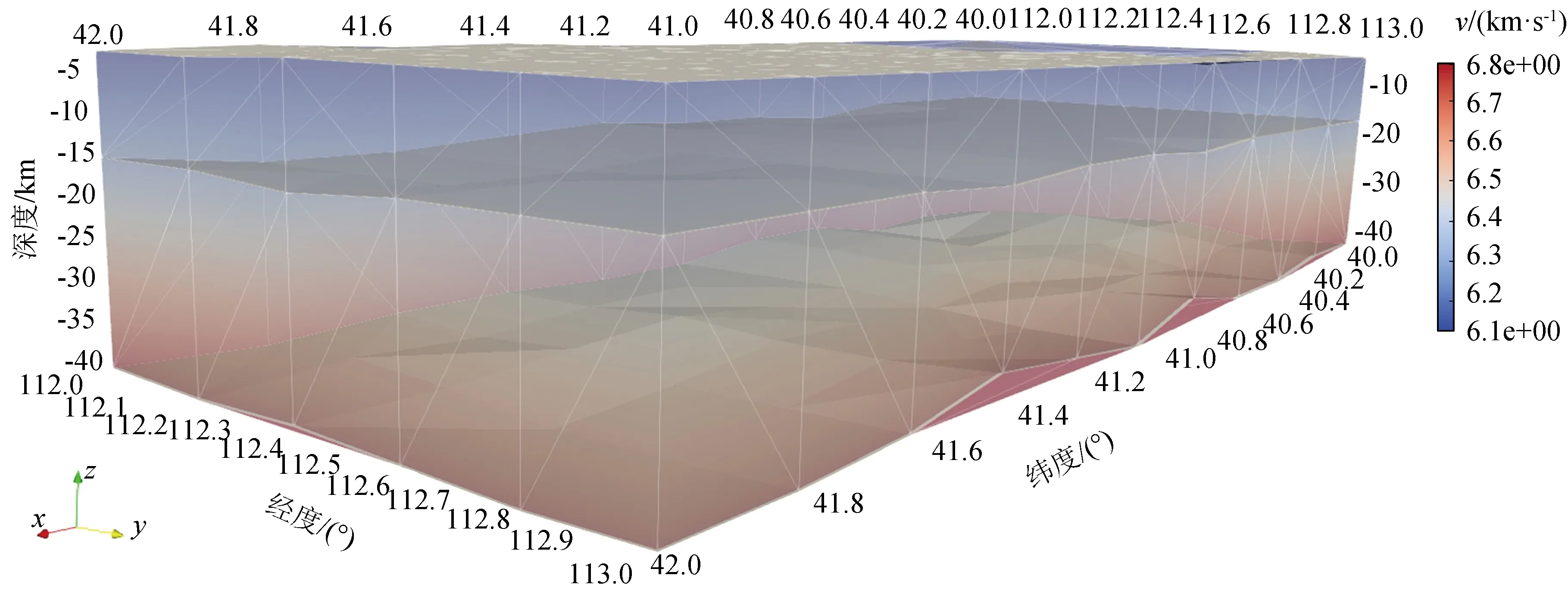
图2 研究区三维地壳速度结构模型Fig.2 Three dimensional crustal velocity structure model in the study area

图2中三维地质结构模型包括了地球内部的主要间断面(上地壳面、中地壳面和下地壳面),x、y、z轴分别代表三维空间的三个方向(纬度、经度、深度)。由图可知,研究区沉积层深度范围大致在0～4.8 km左右,P波波速在6.1 km/s以下;研究区上地壳深度范围在5～15 km左右,P波波速在6.1～6.25 km/s范围之间;研究区中地壳深度范围在15～40 km左右,P波波速在6.25～6.7 km/s范围之间;研究区下地壳深度范围在40 km以上,P波波速在6.7 km/s以上。

利用牛顿迭代法求取群速度,根据最短路径法原理,基于华北克拉通山西断陷带北部局部区域三维地质模型进行射线追踪。

在进行最短路径射线追踪时,需改进连通性的判断算法。设震源点在最低层的一个单元四面体中,对模型中所有的四面体进行连通性判断。在进行两个四面体连通性判断时,可通过如下算法进行判断:

(1)在Paraview的脚本中通过GetCell()方法得到对应单元四面体的索引。

(2)在Paraview的脚本中通过GetPointId()方法得到对应单元四面体的四个顶点坐标。

(3)如果两个四面体都处于同一层地质介质中,则只需判断两四面体的空间点坐标是否有三个共同点,若有三个共同的点,则两个四面体相连通,反之,则不连通。

(4)如果两个四面体分别处于不同的地质介质中,但满足条件(3),则需遵循snell定理判断是否能够发生折射,若未达到临界角,则两个四面体相连通,反之,则不连通。

采用最短路径算法可求出所有与震源连通的节点走时,并找出到检波点用时最小的路径。如图3所示,图中紫线选中的单元分别为震源单元和检波单元,红线即为震源点至检波点的模拟路径。

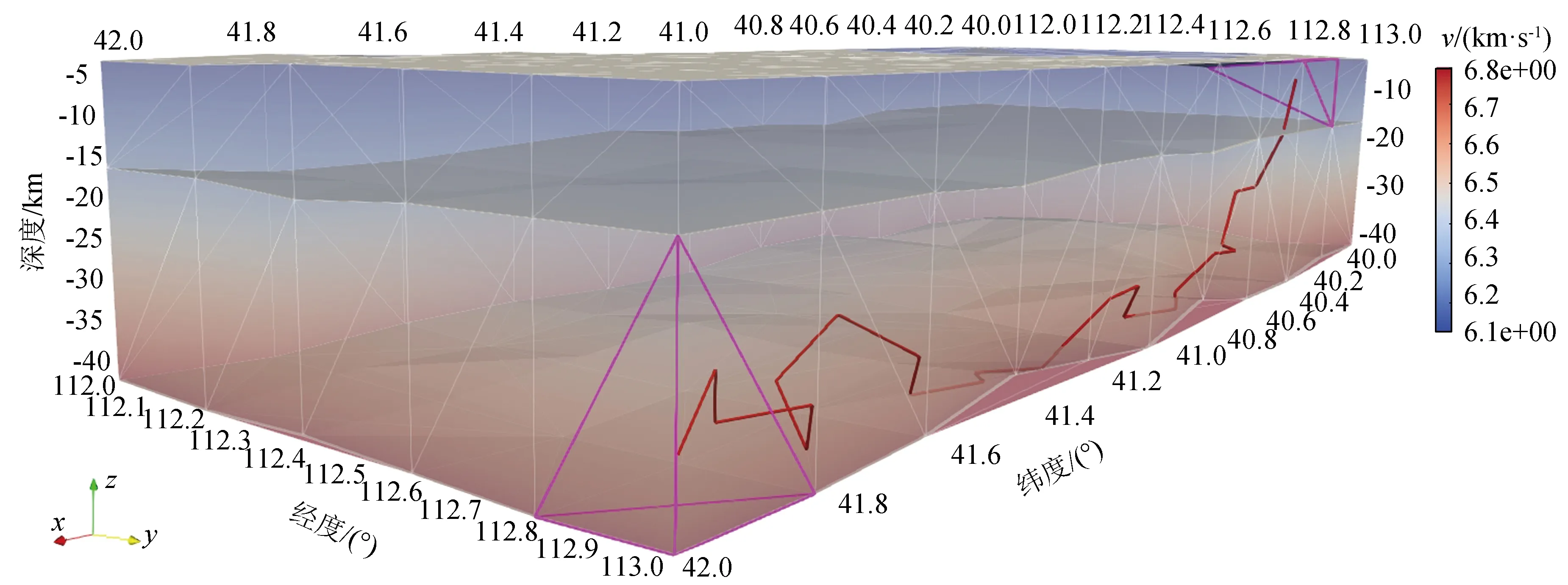
图3 最短路径射线追踪效果图Fig.3 Effect picture of shortest path ray tracing

4 结论

本文基于Paraview平台自动化构建三维地质模型并进行射线追踪模拟,为三维地质模型的构建和地震波射线追踪模拟及可视化提供了一种新思路。根据地下普遍存在各向异性的事实和地震波基本传播规律,利用牛顿迭代法高效求解群速度,并以华北克拉通山西断陷带北部局部区域为例,基于研究区三维地质模型采用最短路径法进行地震波射线追踪模拟及可视化。结果表明,该方法减少了由各向异性对地震波传播带来的影响,清晰表达了研究区地质结构和各向异性特点。

本文方法克服了目前基于二维平面、三维剖面或简单三维空间的各向异性速度结构研究难点,实现地震波在真实地下复杂三维空间传播规律的模拟,充分表达地下速度不均匀性和各向异性,更好地帮助研究人员解读研究区地质结构。

致谢:本研究使用的华北克拉通中部山西断陷带区域速度结构模型数据引自华北地区地壳-上地幔地震波速度结构模型v2.0,(郑天愉、段永红、许卫卫、艾印双、陈凌、赵亮、张耀阳、徐小兵,2015),数据链接网址:http://www.craton.cn/data,在此表示感谢。