层状地基环形沟隔振效果影响因素分析

刘晶磊,刘鹏泉,尚康君,王 洋

(1.河北省土木工程诊断、改造与抗灾重点实验室,河北 张家口 075000;2.河北建筑工程学院,河北 张家口 075000;3.河北省寒冷地区交通基础设施工程技术创新中心,河北 张家口 075000)

0 引言

随着经济的飞速发展,高速列车、地铁等轨道交通运输无论是在载重量还是在运行速度上都得到了极大地提升,且其运行线路范围也在不断地扩大,但同时其产生的振动对临近建、构筑物的影响也在不断加剧,尤其是当列车下穿高架桥时对桥墩支撑稳定性的影响,经过对仪器灵敏度要求极高的实验室、军事重地及医院附近时对仪器测量精度的影响等更为剧烈[1-3],因此对降低振动影响的试验研究具有重要意义。

目前,国内外学者对于降低振动影响进行了大量的研究。Woods等[4]采用现场模型试验,通过将沟槽几何参数无量纲化研究其各参数对隔振效果的影响。Celebi[5]、Yang[6]和Hung等[7]采用数值模型分析沟槽的有无填充及材料特性对屏障隔振性能的影响。结果表明:无填充沟槽的隔振效果要优于填充沟。丁智等[8]为研究双线地铁运营时隔振沟的减振效果,基于2.5维有限元法建立双线地铁列车-轨道-地基土体耦合分析模型。结果表明:空沟隔振中,增加沟深可有效起到隔振效果。高广运等[9]、时刚等[10-11]采用薄层法和半解析动力边界元法分析多层地基土的动力问题。结果表明:空沟屏障隔振可以有效地隔离振动,且空沟深度对隔振效果影响显著。刘晶磊等[12]、郑辉[13]、夏洪春等[14]通过物理模拟测试及数值分析的方法同样研究了空沟几何参数对隔振效果的影响。结果表明:沟槽深度是影响其隔振效果的重要参数,且与其他参数以复杂的关系耦合。

基于以上研究发现,试验内容多数停留于均质地基屏障隔振性能数值分析,现场试验较少,且以矩形沟隔振研究为主,而实际工程条件下地基土层常为非单一土层,同时考虑到高架桥桥墩、医院等重要建、构筑物在隔振系统中类似于对于一个点的保护,因此本文采用室外试验探究了层状地基环形沟深度、宽度及弧长等几何参数变化对其有效隔振区域的影响规律,从而为环形沟隔振设计提供合理化建议。

1 隔振机理

振动荷载作用于土体介质时会产生振动波,振动波主要有三种,分别为P波、S波和瑞利波,且在远场振动中,瑞利波占比67%以上[15],因此本文主要对瑞利波进行频谱分析,研究屏障隔振对瑞利波的衰减规律。

隔振即通过设置屏障来衰减瑞利波的能量传递。本文采用环形沟连续隔振屏障,如图1所示。

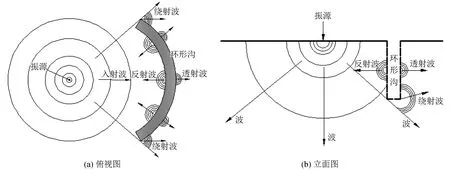
图1 瑞利波的传递机理Fig.1 Transmission mechanism of Rayleigh wave

瑞利波在传递过程中遇到隔振屏障会有部分波被反射回来,形成反射波;较少部分波会透过隔振屏障形成透射波;还有一部分波绕过隔振屏障末端及沟底传递,从而形成绕射波[16-17]。由于此现象的存在,使得振动波的能量被分散,从而可以有效地衰减瑞利波的能量传递,减小瑞利波对隔振屏障保护区域的影响。

2 试验概况

2.1 试验场地及设备

本试验场地主要由40 cm深的上层粉质黏土和120 cm深的下层砂土分层夯实组成,长×宽控制为400 cm×400 cm。为了更接近于工程实际条件[18],控制层状土密度为1 600～1 700 kg/m3,含水率为10%～11%。

如图2、3所示,试验设备主要采用WS-Z30型振动台控制系统。该系统主要由信号发生器、功率放大器、激振器、数据采集控制仪、加速度传感器、加速度计放大器、电荷放大器等组成,其中加速度传感器的灵敏度和测量范围分别为4 PC/ms-2和50 m/s2。主要工作流程为:首先,由信号发生器生成指定频率的周期性信号,并经功率放大器放大传到激振器中的驱动线圈上使其激发试验所需的振动波,然后由加速度传感器接受振动信号并经加速度计放大器放大传递到数据采集控制仪进行数据处理分析。

图2 试验相关设备Fig.2 Test related equipment

图3 场地设备布置Fig.3 Site equipment layout

2.2 试验方案

本试验主要探究了层状地基土条件下环形沟深度、宽度、弧长等几何参数变化对其有效隔振区域的影响,其中弧长参数的选取分别对应环形沟圆心角90°、120°及150°,激振频率采用10～150 Hz,每间隔10 Hz逐级激振,采样频率设置为5 000 Hz,时间为5 s。相关试验变量列于表1。

表1 试验变量Table 1 Test variables

如图4所示,由于环形沟隔振影响区域关于0°轴线对称,所以只需探究环形沟隔振影响区域的一侧0°～80°区域即可,本试验以0°轴线开始顺时针每间隔10°布置一组传感器进行激振信号接收,共布置9组,其中在跨过沟的轴线上布置12个传感器,距激振器由近到远分别命名为1#～12#传感器,未跨过沟的轴线上共布置14个传感器,并且环形沟前后两侧传感器距沟边缘及各相邻传感器间距均保持为15 cm。

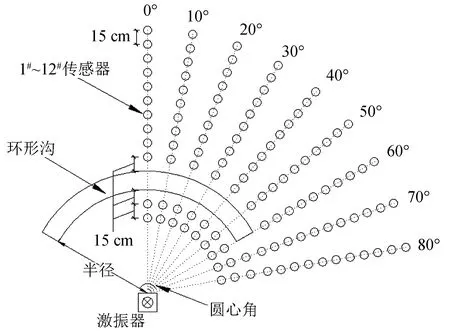
图4 现场布置图Fig.4 Site layout

2.3 评价指标

(1)隔振效果评价指标

本试验采用振幅衰减比Ar值及有效隔振区域占比η评价环形沟不同几何参数条件下其沟后隔振效果。Ar值越小或η越大,代表其隔振效果越好。其表达式为:

(1)

(2)

式中:a1表示设置隔振屏障后相应位置处的竖向加速度值;a0表示未设置隔振屏障时相应位置的竖向加速度值;基于徐平等[19-20]对有效隔振区域范围的界定,本文针对环形沟隔振,将沟后Ar≤0.4的范围区域定义为有效隔振区域,以A0.4表示;A表示环形沟后传感器布置区域面积。

(2)参数分析指标

本试验中,将环形沟几何参数与振动波波长作对比,实现无量纲分析,以此分别引入深度参数D、宽度参数W及弧长参数L等。其表达式为

(3)

(4)

(5)

式中:d为环形沟深度;w为环形沟宽度;l为环形沟中心线弧长;λR为瑞利波波长。

2.4 瑞利波长的确定

试验采用表面波频谱分析法测试土层瑞利波速。如图5所示,周期性激振荷载作用下,瑞利波在振源处产生,并经1#传感器向2#传感器往外传播,设1#和2#传感器接收到的时域信号分别为x(t)和y(t),则1#到2#传感器之间的时间滞后即为瑞利波从1#到2#传感器的传播时间,由于瑞利波在成层地基中的传播速度是随波长或激振频率改变的(弥散性)[21-22],因此只有通过频谱分析,才能确定x(t)和y(t)间的时间滞后。x(t)和y(t)的谱密度分别为:

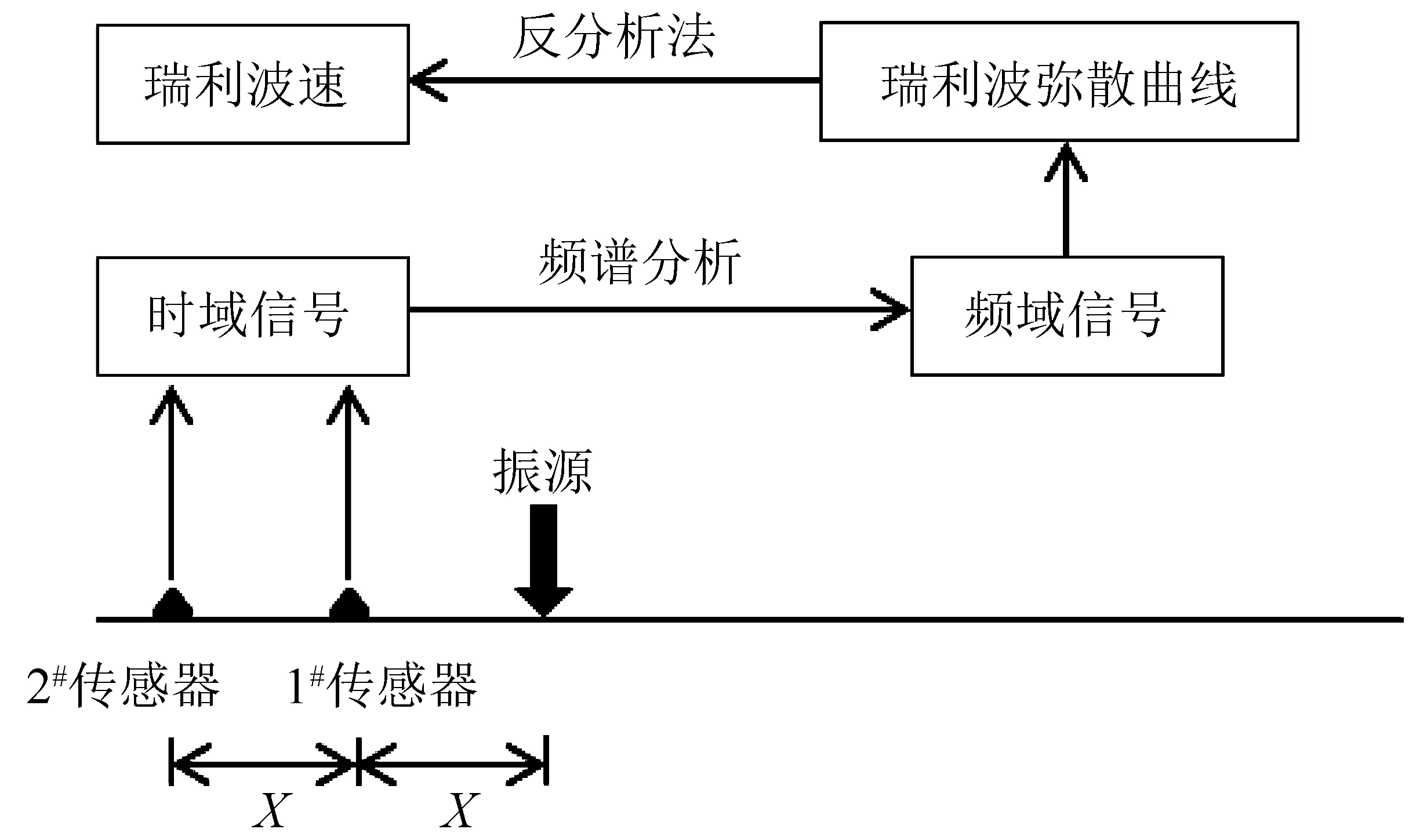
图5 表面波频谱分析法Fig.5 Surface wave spectrum analysis method

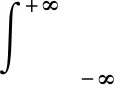
(6)

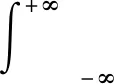
(7)

x(t)和y(t)间的互功率谱为:

(8)

(9)

x(t)和y(t)的相干函数定义为:

(10)

γ(f)在某频段上接近1,表示x(t)和y(t)在该频段上具有良好的相关性。

如图5,设两传感器间的距离为X,瑞利波沿1#和2#传感器所在位置直线传播,所以其速度可表达为:

(11)

依据波速、频率和振动波长存在下式关系,可得出不同频率下瑞利波的波长:

(12)

将试验结果带入式(10)与(11)可得到瑞利波波速,瑞利波波速取均值为127.30 m/s;将瑞利波速带入式(12)可计算出瑞利波波长,经计算瑞利波波长最大值为12.73 m,最小值为0.85 m。

3 试验结果分析

为了探究层状地基土环形沟深度、宽度及弧长参数变化对其有效隔振区域的影响规律,本文控制环形沟中线与振源的垂直距离为120 cm,采用10～150 Hz激振频率,每间隔10 Hz逐级激振,并以Ar二维等值线图对中频80 Hz激振时环形沟几何参数变化对其有效隔振区域影响规律作具体分析,其他频率作为校核对照,不在文中赘述。最后以环形沟不同几何参数在10～150 Hz激振频率条件下有效隔振区域占比η与其相对应几何参数进行拟合分析,得出其影响规律,并对设计施工做出合理化建议。

3.1 环形沟深度对有效隔振区域影响

为了探究环形沟深度对有效隔振区域影响,试验中控制环形沟宽度为20 cm,弧长为251.2 cm,将深度参数作为变量进行相关分析。试验结果如图6所示。

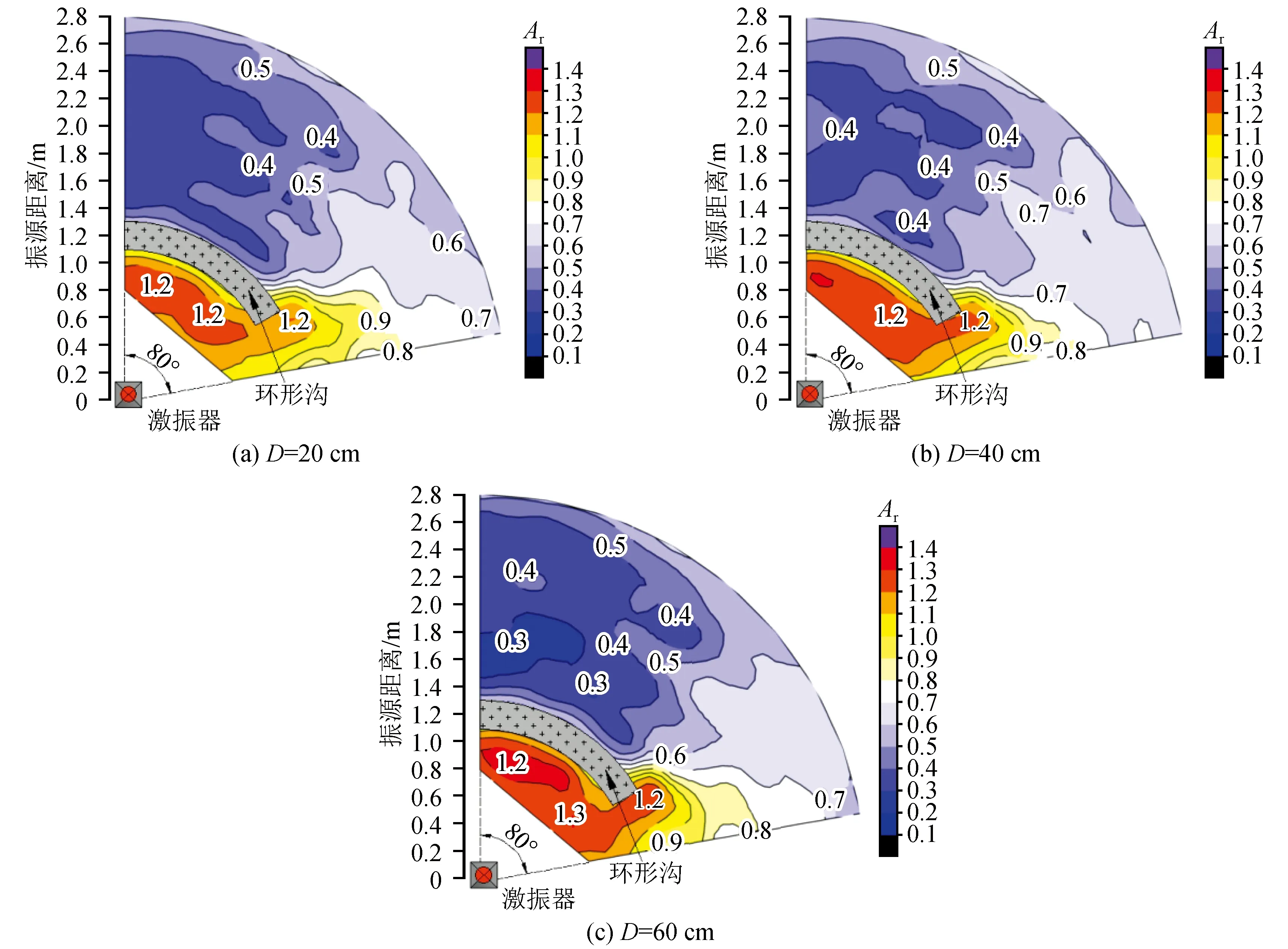
图6 不同深度参数Ar值二维等值线图Fig.6 Two-dimensional contour map of Ar value with different depth parameters

由图6,当环形沟深度参数在0.16～0.71之间不断增大时,在振源激振作用下,环形沟后形成不同Ar值变化区间的隔振区域,且Ar≤0.4的有效隔振区域呈现先减小后增大的变化规律;如图6(b)所示,当环形沟深与上层土厚相等时,有效隔振区域范围比较分散;如图(c)所示,当深度参数达到0.71时,出现Ar≤0.3的有效隔振区域。

激振器与环形沟之间及环形沟末端一侧区域Ar值保持在1.10～1.40间,且随深度参数的增加,该区域Ar值也随之增大。由此可知环形沟前及沟末端由于瑞利波的反射及绕射现象的存在,造成波的叠加而出现振动放大区。

关于有效隔振区域占比η随深度参数D变化拟合关系曲线如图7所示。其拟合回归方程为:η=5.04lnD+71.6,自由度为45,相关系数为0.82。

由图7,当深度参数在0.16～0.71之间不断增加时,有效隔振区域占比η在50.5%～70.0%之间呈逐渐增大趋势,变化幅度达19.5%,但出现当环形沟深度与上层土厚相等时对应深度参数下的有效隔振区域占比η均分布在了拟合线下侧的现象,即此时相对于其他深度参数,有效隔振区域面积出现了衰减。

图7 η随深度参数变化拟合关系曲线Fig.7 Fitting relationship curve of η with the change of depth parameter

综上分析可知,层状地基土环形沟隔振中,环形沟深度参数是影响其有效隔振区域的重要参数,且深度参数越大有效隔振区域面积越大,即隔振效果越好,但当环形沟深接近于上层土厚时,其有效隔振区域相对减小,隔振效果相对减弱。因此建议在环形沟隔振设计中,在保证稳定性的前提下应尽量增大环形沟深度参数,并避免将环形沟开挖到土层分界面附近。

3.2 环形沟宽度对有效隔振区域影响

为了探究环形沟宽度对有效隔振区域影响,试验中控制环形沟深度为60 cm,弧长为251.2 cm,将宽度参数作为变量进行相关分析,试验结果如图8所示。

由图8,当环形沟宽度参数在0.01～0.35之间增大时,有效隔振区域相差不大,但Ar≤0.3的有效隔振区域呈现出随宽度参数增加而不断增大的变化规律,且主要分布在沟后临近沟的位置;环形沟前及末端振动放大区域及强度随宽度参数的增加而增加,且其差异主要体现在环形沟末端。

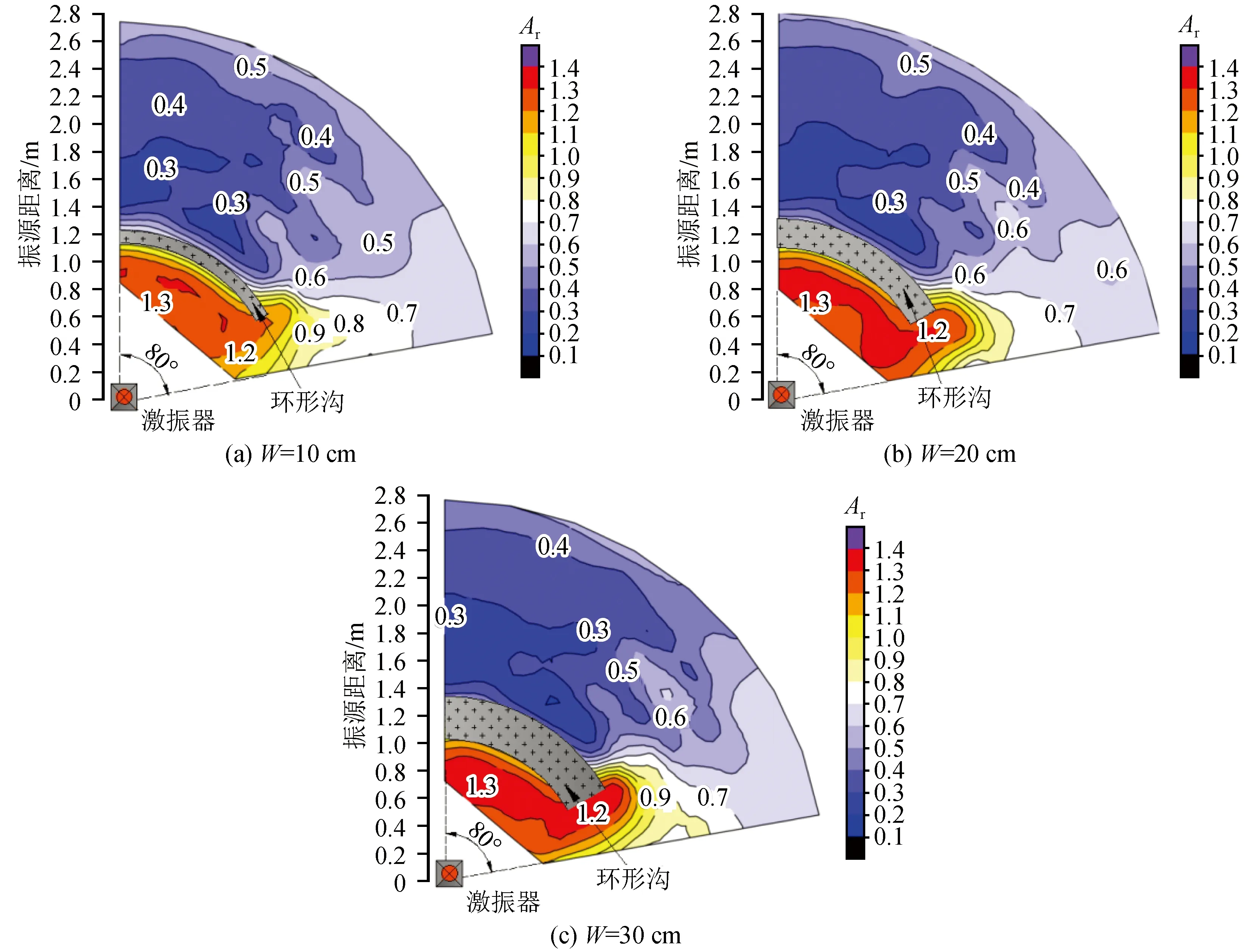
图8 不同宽度参数Ar值二维等值线图Fig.8 Two-dimensional contour map of Ar values with different width parameters

关于有效隔振区域占比η随宽度参数W变化拟合关系曲线如图9所示。其拟合回归方程为:η=1.29lnW+65.9,自由度为45,相关系数为0.96,接近于1,拟合良好。

由图9,宽度参数在0.01～0.35之间增大时,有效隔振区域占比η随宽度参数的增大而增大,但增大幅度较小,仅变化4.8%,这是因为环形沟宽度参数增加会在一定程度上衰减透射波的能量,但瑞利波传递过程中,透射波占比非常小,所以环形沟宽度参数的变化对其有效隔振区域影响很小。

图9 η随宽度参数变化拟合关系曲线Fig.9 Fitting relationship curve of η with the change of width parameter

综上分析可知,由于环形沟宽度参数不是影响其有效隔振区域的重要参数,因此在实际工程设计中,考虑到经济适用,建议将环形沟宽度设计为较小值即可。

3.3 环形沟弧长对有效隔振区域影响

为了探究环形沟弧长对有效隔振区域影响,试验中控制环形沟深度为60 cm,宽度为20 cm,将弧长参数作为变量进行相关分析,试验结果如图10所示。

由图10,当环形沟弧长参数在0.15～3.70之间增大时,其有效隔振区域随弧长参数的增大而增大;环形沟前振动放大区域及强度随弧长参数的增加而增加,沟末端振动放大区域及强度随弧长参数的增加而减小,这是因为弧长参数增加,会对环形沟末端一部分绕射波起到阻挡反射作用,从而使得沟前叠加更多的振动波,沟末端振动波减少。

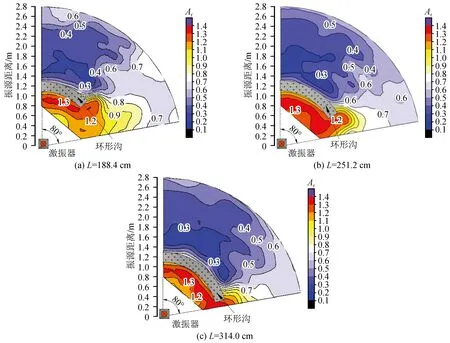
图10 不同弧长参数Ar值二维等值线图Fig.10 Two-dimensional contour map of Ar values with different arc length parameters

关于有效隔振区域占比η随弧长参数L变化拟合关系曲线如图11所示。其拟合回归方程为:η=4.4lnL+64.2,自由度为45,相关系数为0.97,接近于1,拟合良好。

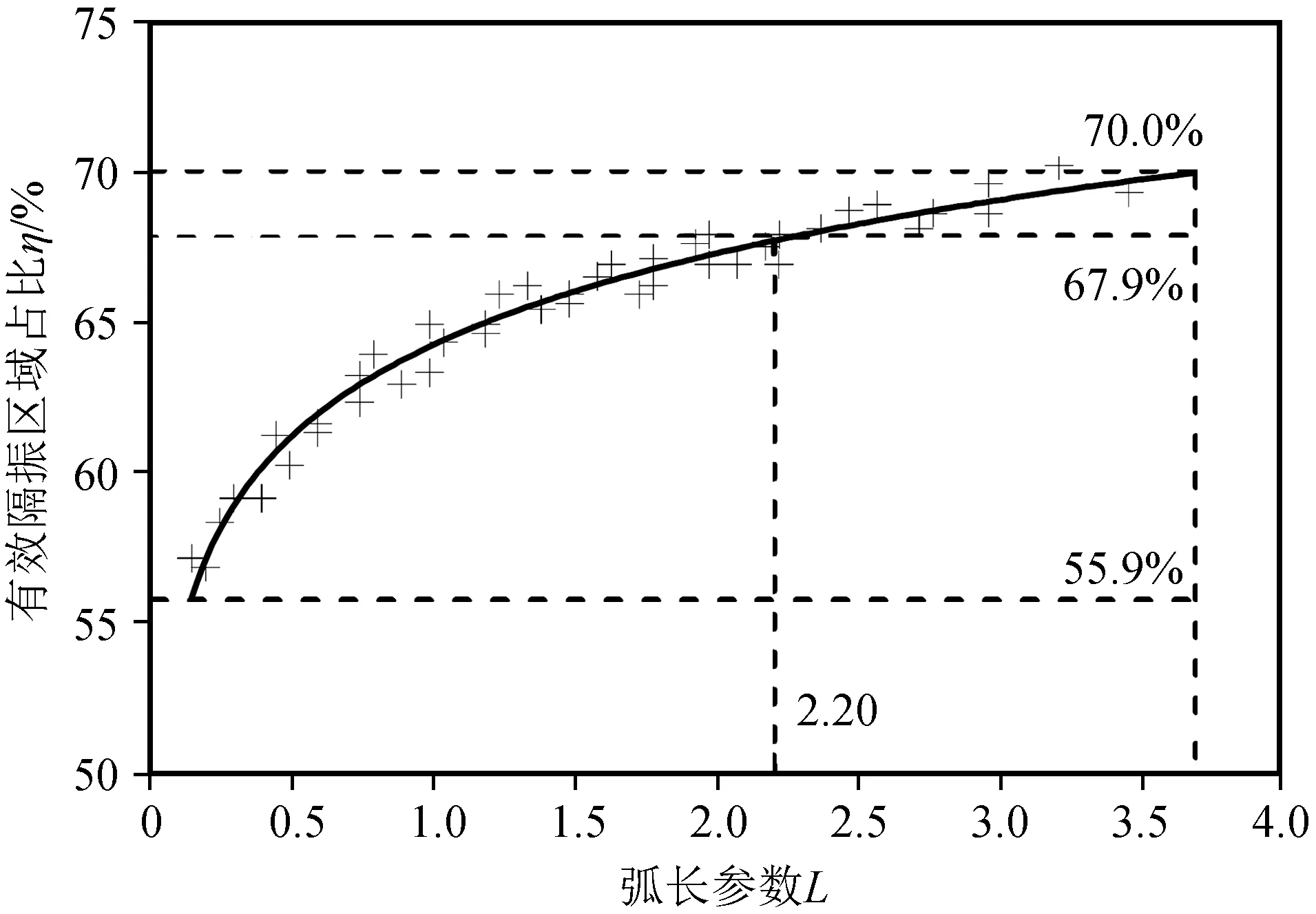
图11 η随弧长参数变化拟合关系曲线Fig.11 The fitting curve of η with the change of arc length parameter

由图11分析可知,弧长参数在0.15～3.70之间增大时,有效隔振区域占比η随弧长参数的增大而增大,变化幅度为14.1%,其中当弧长参数在2.20～3.70之间变化时,有效隔振区域占比η仅变化2.1%。

综上分析可知,环形沟弧长参数是影响其有效隔振区域的重要参数,且弧长参数越大,有效隔振区域面积越大,当弧长参数达到2.20后,环形沟有效隔振区域面积趋于稳定,因此限于本试验条件,建议环形沟隔振设计中弧长参数取为2.20左右。

4 结论

本文通过室外试验的方法对层状地基土中环形沟深度、宽度及弧长参数变化对其有效隔振区域影响规律进行了探究分析,结论如下:

(1)环形沟深度参数是影响其隔振效果的重要参数,且深度参数越大隔振效果越好,但当环形沟深度接近于上层土厚时,环形沟隔振效果相对减弱,因此在环形沟隔振设计中,建议增大深度参数,并尽量避免开挖到土层分界面处。

(2)环形沟宽度参数不是影响其有隔振效果的重要参数,因此在环形沟隔振设计中,考虑到经济适用,宽度参数设为较小值即可。

(3)环形沟弧长参数也是影响其隔振效果的重要参数,且弧长参数越大隔振效果越好,但当弧长参数达到2.20以后,隔振效果趋于稳定,因此在环形沟隔振设计中,建议弧长参数取为2.20左右。

(4)环形沟前及沟末端存在振动放大区域,且其强度与环形沟几何参数的大小有关。