圆柱形货物三维装箱问题简便解法

贾春玉，朴惠淑，温 良

(1. 广东培正学院 管理学院, 广州510830 2. 大连海事大学 交通运输工程学院， 辽宁 大连116026) 3. 长春大学 管理学院，长春 130022)

一、主要问题

圆柱形货物平面摆放方式有对齐摆放方式、紧凑压缝摆放方式和松散摆放方式等形式。三维分层装箱(摆放)也有对齐摆放方式、紧凑压缝摆放方式和松散摆放方式等形式。组合摆放比条块状货物摆放得多且复杂，因此圆柱形货物三维装箱问题是比条块状货物装箱问题更为复杂的难题。货物装箱下料问题的研究成果众多[1-2]，但针对圆柱形货物装箱问题的研究成果非常少，而针对圆柱形货物三维装箱问题的研究成果就更少，几乎查不到相关的文献，能查到的相关文献多数为圆形货物二维下料问题[3-4]，且多数为递归智能解法。虽然装箱与下料问题互为反问题，有些方法可以互用，但还是有明显区别的，其主要区别是下料问题具有最大毛坯排数限制、切割宽度损耗等，在许多情况下不能直接互用，因此有必要研究圆柱形货物装箱问题。传统的方法是人们凭经验装箱或下料，存在优化程度低、成本高等弊端。为了解决这些问题，学者们提出了多种解法，如动态规划算法[5-6]、启发式递归解法[7-8]等。这些方法虽然可以解决这类问题，但通常需要建立较为复杂的数学模型和编制求解软件进行求解，不易掌握。为了更好地解决这一问题，本文提出新的线性规划解法，该方法简单、易于掌握、优化程度高。因为紧凑压缝摆放方式优化程度通常较高、货垛稳定、摆放规律性强、摆放效率高，所以这里只针对这种摆放方式提出新的简便解法。

(一)竖立摆放时三维装箱解法

货物有时要求必须竖立摆放，尤其是圆柱形容器装满货物时更是如此。在这种情况下，三维装箱相对比摆放无约束时简单，只需按要求优化求解出按货箱高度方向竖立摆放一层的优化数量，再乘以货箱按高度方向能摆放的层数即可。因此，首先是求解出平面二维优化摆放数量，然后计算出能摆几层，最后根据两者乘积得出总的摆放数量。

单一圆柱形货物平面放的三种摆放方式在一定条件下均可能是最佳摆放方式。在摆放方式的组合上，可以是单一一种摆放方式，也可以是两种或两种以上摆放方式的组合，垛高方向可以是与货箱长度方向相同，也可以是与货箱宽尺寸方向相同，择优作为最终优化方案，获得平面摆放近似最优解，据此获得三维摆放近似最优解。

(二)摆放无约束时三维装箱解法求解思路

总体求解思路是分别按货箱长J1、宽J2和高J3三个维度优化摆放，将三个维度优化方案择优为最终优化方案，获得满意近似最优解。每个维度优化时可分为两个阶段，以最终按货箱高度优化为例，求解过程分为两个阶段：第一阶段是求出按货物直径和高度尺寸每摆一层的优化摆放数量；第二阶段是按货箱高尺寸三维优化求解。第一阶段的求解步骤为：计算货物两个维度的尺寸(直径和高度)每层摆放数量，即在货箱长和宽的二维平面内，先计算按货物直径尺寸摆放一层的优化摆放数量，此时的货物可用尺寸是直径和高度，暂时把货物直径尺寸视为矩形货物的长(H1)，货物高度尺寸视为货物的宽(H2)，货箱可用尺寸是货箱的长和宽，选用一种或几种优化摆放方式进行优化求解，择优得出按货物直径尺寸摆放一层的数量；再计算按货物高度(如桶高)摆放一层的优化摆放数量，此时的货物可用尺寸是直径，货箱可用尺寸是货箱的长和宽，选用一种或几种优化摆放方式进行优化求解，择优得出一层货物高的摆放数量。第二阶段的求解步骤为：按货物直径摆放一层和按货物高度摆放一层的优化摆放数量，再按货箱高度进行三维立体优化摆放，优化求解各摆多少层，使总的摆放数量最多，得出近似最优解。其他两个维度(按货箱的长和宽)优化类似，三个维度优化结果择优作为最终优化结果。

(三)求解过程

以按货箱高度三维立体优化为例，详细介绍求解过程。其他两个维度优化与高度优化类似，所以只作概略介绍，只介绍第二阶段求解的数学模型。

1.按货箱高度三维优化求解过程

(1)第一阶段求解过程及数学模型。摆放方式有单一紧凑摆放方式、组合紧凑摆放方式、单一松散摆放方式和组合松散摆放方式；优化方法有数量优化方法[9]、边长优化方法[9]、5块法[10]、线性规划解法和非线性规划解法等。这里只介绍最简单、摆放效率最高的单一紧凑摆放方式，虽然该方法优化程度略低，但简单、实用、装箱效率高。

首先，按货箱长二维优化时规划求解数学模型。

单一紧凑摆放方式是指货物在平面内只有一种摆放方式，如压缝摆放方式1(按货箱长J1优化摆放，即垛高为货箱长J1方向)；压缝摆放方式2(按货箱宽J2优化摆放，即垛高为货箱宽J2方向)，列出优化数学模型求解，两种摆放方式优化程度择优作为优化结果。

模型1：按货箱长二维优化时按货物直径尺寸摆一层的数学模型

设货物“长”为(直径)H1=2R，“宽”(货物高)为H2；货物“长”对货箱长摆放个数为N11，对货箱宽摆放个数为N12；货物“宽”对货箱长摆放个数为N21，对货箱宽摆放个数为N22。X11为货物“长”摆放的列数(按货箱长方向摆放个数)，X21为货物“宽”摆放的列数(按货箱长度方向摆放个数)，总的摆放数量为ZQ1。为了简化问题，暂不考虑剩余空间可摆放数量(计算例题中考虑了)，则数学模型如下[9]。

目标函数：MaxZQ1=X11×N22+X21×N12

约束条件:X11×H1+X21×H2≤J1

X11、X21为正整数。

在符号Nij中，i代表货物维度，1代表货物的“长”，2代表货物的“宽”; j代表货箱维度，1代表货箱长，2代表货箱宽。则有如下计算公式：

Nij=[Jj/Hi]1

符号“[ ]1”代表向下取整。

例如:N12= [J2/H1]1，代表货物“长”在货箱“宽”方向上最多可摆放的个数。

模型2：按货箱长二维优化时按货物高摆一层的数学模型

圆柱形货物半径R，对齐摆放一层高度为2R(参见图1，参见图2和图3，带方格线部分)、压缝单数和双数层一层高度为H(参见图2和图3，带底色为压缝单数层，无底色、无方格线为双数层)，对齐摆放、压缝单数摆放和压缝双数摆放层对应3个变量。设按货箱长度J1优化时(压缝摆放方式1)圆柱形货物对齐摆放、压缝单数层、压缝双数层3个变量分别为X11、X21、X31, 按货箱宽尺寸方向货物对齐、压缝单数层、压缝双数层每层摆放个数(已知数)分别为N11、N21、N31, 总的摆放数量为GQ1，则数学模型如下。

图1 上下对齐摆放方式

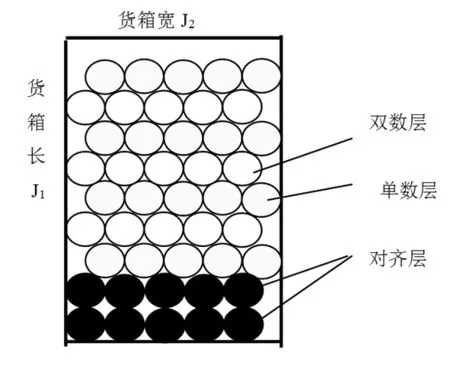
图2 压缝摆放方式1

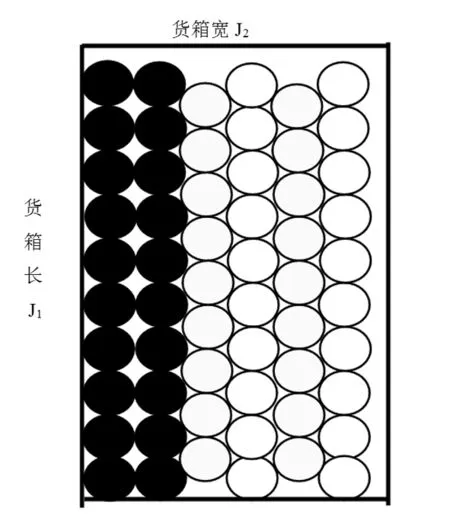
图 3 压缝摆放方式2

目标函数：MaxGQ1=X11×N11+X21×N21+X31×N31

S．T．X11×2R+X21×H+X31×H≤J1

X21≥X31

X21-X31≤1

X11≥1

变量为非负整数。

其中，H=30.5R，N11= N31=[J2/2R]1,N21=[(J2-R)/2R]1; 变量Xij和Nij中的下角标i代表第i个变量(i=1，2，3)，1、2、3分别代表对齐、压缝单数、压缝双数层；j代表货箱维度(j=1，2)，1和2分别代表按货箱长度J1和宽度J2优化时的对应变量或摆放个数。以下类似符号代表意义相同。

其次，按货箱宽二维优化时规划求解数学模型。

模型1：按货箱宽二维优化时按货物直径摆一层的数学模型

设X12为货物“长”摆放的列数(按货箱宽尺寸方向摆放个数)，X22为货物“宽”摆放的列数(按货箱宽尺寸方向摆放个数)，总的摆放数量为ZQ2。为了简化问题，暂不考虑剩余空间可摆放数量(计算例题中考虑了)，则数学模型如下[9]。

目标函数：MaxZQ2=X12×N21+X22×N11

约束条件:X12×H1+X22×H2≤J2

X12、X22为正整数。

模型2：按货箱宽二维优化时按货物高摆一层的数学模型

设按货箱宽J2优化时(压缝摆放方式2), 圆柱形货物对齐摆放、压缝单数层个数、压缝双数层个数3个变量分别为X12、X22、X32，按货箱长度方向货物对齐、压缝单数层、压缝双数层每层摆放个数(已知数)分别为N12、N22、N32，总的摆放数量为GQ2，则数学模型如下。

目标函数：MaxGQ2=X12×N12+X22×N22+X32×N32

S．T．X12×2R+X22×H+X32×H≤J2

X22≥X32

X22-X32≤1

X12≥1

变量为非负整数。

其中，H=30.5R，N12= N32=[J1/2R]1、N22=[ (J1-R)/2R]1，符号“[ ]1”为向下取整。

最后，最终二维优化结果。

按货物高摆一层最终优化结果(GQ3)：

GQ3=Max(GQ1，GQ2)

按货物直径摆一层最终优化结果(ZQ3)：

ZQ3=Max(ZQ1，ZQ2)

(2)第二阶段求解过程及数学模型。设按货箱高尺寸三维优化时货物直径尺寸摆X1层，货物高尺寸摆X2层，优化摆放数量为Q3，则按货箱高尺寸三维优化时数学模型如下[9]。

目标函数：MaxQ3=X1×ZQ3+X2×GQ3

约束条件:X1×H1+X2×H2≤J3

H1=2R

X1、X2为正整数。

2.按货箱宽尺寸优化求解过程

按货箱宽尺寸优化求解过程与按货箱高尺寸优化求解过程类似，只需把平面二维优化时的货箱尺寸换成货箱长和高的尺寸，再按货箱宽尺寸进行三维优化，优化结果为Q2，设ZQ2和GQ2分别为按货箱宽尺寸三维优化时按货物直径和高度尺寸平面优化摆放数量。为了节省篇幅，第一阶段求解过程及数学模型从略，设按货箱宽尺寸三维优化时货物直径尺寸摆X1层、货物高尺寸摆X2层，则按货箱宽尺寸三维优化时的数学模型如下[9]。

目标函数：MaxQ2=X1×ZQ2+X2×GQ2

约束条件:X1×H1+X2×H2≤J2

H1=2R

X1、X2为正整数。

3.按货箱长尺寸优化求解过程

按货箱长尺寸优化求解过程与按货箱高尺寸优化求解过程类似，只需把平面二维优化时的货箱尺寸换成货箱宽和高的尺寸，再按货箱长尺寸进行三维优化，优化结果为Q1，设ZQ1和GQ1分别为按货箱长三维优化时按货物直径和高度尺寸平面优化摆放数量。为了节省篇幅，第一阶段求解过程及数学模型从略，设按货箱长尺寸三维优化时货物直径尺寸摆X1层，货物高尺寸摆X2层，则按货箱长尺寸三维优化时的数学模型如下[9]。

目标函数：MaxQ1=X1×ZQ1+X2×GQ1

约束条件:X1×H1+X2×H2≤J1

H1=2R

X1、X2为正整数。

4.最终三维优化结果

取按货箱三维优化结果最好的作为最终优化结果ZQ。

ZQ=Max(Q1，Q2，Q3)

最优解下限LQ=[(J1×J2×J3)/(3.14159×R2×H2)]1

优化程度=(ZQ/LQ) ×100%

二、求解实例

实例1: 货箱长(J1)1200cm，宽(J2)234cm，高(J3)269cm,货物为半径(R)21cm的圆柱形，圆柱高(H2)31cm，问圆柱形货物摆放无约束情况下最多能摆多少货物？

解：最优解下限LQ=[(1200×234×269)/(3.14159×212×31)]1=1758, 经计算得知，在三维立体优化中按货箱宽尺寸三维优化最好，所以二维优化时只用到货箱长和高的尺寸。在货箱长和高的二维优化中，用数量优化方法按货物直径尺寸摆放一层时按货箱高尺寸优化摆放最多，按货物直径每一列可摆38个，优化摆4列；按货物高尺寸每一列可摆28个，优化摆3列，两种摆放方式优化组合一共摆236个。按货物高尺寸摆放一层时，按货箱高尺寸优化摆放最多，在二维摆放中对齐层每层摆放28个，优化摆放2层；单数层每层摆放28个，优化摆放3层；双数层每层摆放28个，优化摆放2层，按货物高尺寸摆一层时优化组合共可摆196个。

在三维立体优化中，按货箱宽尺寸优化，按圆柱直径尺寸每层可摆236个，优化摆1层；按圆柱高尺寸每层可摆196个，优化摆6层：两种方式共可摆1412个，优化程度为80.32%。而用其他优化方法(如5块法[10])，在二维平面优化中按货物直径尺寸摆放一层时，按货箱高尺寸优化摆放最多，可摆239个，比简便解法多3个；按货物高尺寸摆放数量一样，三维立体优化也是按货箱宽尺寸优化最好，可摆1415个，优化程度为80.49%，仅多0.17%，差别不大。

实例2: 货箱长(J1)960cm，宽(J2)234cm，高(J3)242cm,货物为半径(R)16cm的圆柱形，圆柱高(H2)40cm，问圆柱形货物摆放无约束情况下最多能摆多少货物？

解：最优解下限LQ=[(960×234×242)/(3.14159×162×40)]1=1689, 经计算得知，在三维立体优化中按货箱高尺寸三维优化最好，所以二维平面优化中只用到货箱长和宽的尺寸。二维优化时，用数量优化方法按货物直径尺寸摆放一层时按货箱宽尺寸优化摆放最多，按货物直径每一列可摆24个，优化摆6列；按货物高度尺寸每一列可摆30个，优化摆1列：两种方式优化组合共摆174个。按货物高尺寸摆放一层时，按货箱宽尺寸优化摆放最多，在二维摆放中对齐层每层摆放30个，优化摆放2层；单数层每层摆放29个，优化摆放3层；双数层每层摆放30个，优化摆放3层，按货物高尺寸摆一层时优化组合共可摆237个。

在三维立体优化中，按货箱高尺寸三维优化，按圆柱直径尺寸每层可摆174个，优化摆0层；按圆柱高尺寸每层可摆237个，优化摆6层：两种方式优化组合共可摆1422个，优化程度为84.19%。而用其他优化方法(如5块法[10])，也是按货箱高尺寸优化最好，可摆1422个，优化程度为84.19%，结果一样。

三、结论

根据圆柱形货物的特点及紧凑压缝摆放方式优化程度高、货垛稳定、摆放规律性强、摆放效率高等特点，为了克服现有圆柱形货物二维装箱问题解法相对复杂、不易掌握、三维立体装箱缺乏有效解法困境，提出新的简便线性规划解法。经比较，虽然优化程度有时比非线性规划解法略低，但结果仍然相当理想，可有效克服非线性规划解法求解时间长、经常出现局部最优解、求解效率低等弊端。新的线性规划解法相对简单、容易理解、易于掌握、优化程度高，求解效率也高，运用Excel软件就可快速求解，可有效解决圆柱形货物摆放无约束这类复杂NP难问题。