自动化集装箱码头AGV调度与换电双层模型求解

赵 涛， 梁 承 姬， 胡 筱 渊， 王 钰

( 上海海事大学 物流科学与工程研究院， 上海 201306 )

0 引 言

为建设绿色港口，降低碳排放，大部分自动化集装箱码头采用纯电力驱动的自动导引车(automated guided vehicle，AGV)承担集装箱在码头内部的水平运输任务，连接岸边作业系统与堆场作业系统．电力驱动AGV是特殊工作环境下的电动汽车．当AGV可用电量低于换电阈值(安全电量)时，必须充电，否则随时有可能停止运行，从而影响集装箱码头正常作业．因此，AGV充电是自动化集装箱码头不可忽略的重要问题．

自动化集装箱码头投产以来，AGV调度问题备受学者青睐．Confessore等[1]利用最小流模型分析了AGV调度问题；王聪等[2]建立了双层规划模型研究AGV作业效率和能源消耗；Choe等[3]提出了在线学习算法对AGV进行实时调度；霍凯歌等[4]以最小化作业总费用为规划目标研究了多载AGV的调度问题．大部分学者在研究AGV调度问题时，往往忽略了电量约束．随着AGV充电问题的重要性日趋显现，部分学者开始关注AGV充电问题．如刘广红等[5]分析了上海港洋山四期自动化码头的总体布局，以及换电站的分布和容量设置；傅正堂等[6]考虑AGV耗电差异，研究了AGV电量非饱和状态下的调度优化；石楠路等[7]构建了混合整数优化调度模型，提出了AGV作业顺序和换电站时间窗协同的换电策略，并用遗传算法求解验证了模型的有效性；丁一等[8]考虑AGV装载能力和充电后续航能力约束，构建了多载AGV动态作业调度的混合整数规划模型．但现有AGV换电问题的研究成果仍没有关于深入分析AGV调度和换电关系的内容．

充电问题是电池驱动工具无可避免的问题，并且充电问题和调度问题在电动汽车和无人机领域已有较多研究成果．如Barco等[9]综合考虑电池包退化、充电过程等因素，研究了电动汽车路线问题；Shao等[10]综合考虑电动汽车的电量消耗、充电站数量和车辆负载，研究了电动汽车的路线问题；袁泉等[11]分析了电动汽车路网交通信息和电网运行状态的交互影响，并提出了路网-电网耦合原则以调节输电线路阻塞问题；Thibbotuwawa等[12]以最大程度降低能耗为目标研究了电量、无人机重复调用和有效荷载约束下的无人机调度问题；Liu等[13]考虑UAV充电时间和能耗的共同优化，建立了无线充电下无人机最小能耗优化模型．

综上所述，大部分AGV调度相关文献中没有考虑电量约束和充电过程，少部分文献考虑电量约束，但没有考虑换电站的数量和容量限制等因素．本文针对有多个换电站的自动化集装箱码头，综合考虑AGV重、空载耗电差异和换电站的数量、容量限制等约束，分析AGV调度和换电之间相互影响的内在关系，建立AGV调度和换电的双层耦合模型，生成AGV调度和换电方案．

1 问题描述

自动化集装箱码头纯电动AGV的充电方式可分为桩式充电、非接触式充电和换电式．桩式充电必须建设专用场地．非接触式充电方式如图1(a)所示，无须专用场地，AGV在堆场交互区工作间隙补充电量，实现了车辆非停车充电，但充电率有限；换电式如图1(b)所示，必须建设专用换电站，待换电AGV空载驶向换电站，换电机器人为AGV更换电池包．本文研究的自动化集装箱码头AGV充电问题均为换电式的AGV充电问题．

自动化集装箱码头的布局方式主要分为平行式和垂直式，具体细分为5类：双车道平行式、单车道平行式、两端车道垂直式、两侧车道垂直式和U形车道垂直式[14-15]．研究表明，垂直式布局比平行式布局更利于发挥自动化设备的作业性能，且垂直式布局使用广泛，如澳大利亚布鲁斯班码头、荷兰鹿特丹ECT码头、英国伦敦Gateway码头、德国汉堡CTA码头等[16-17]．

本文以上海港洋山四期自动化码头实际布局为基础(图2)，研究两端车道垂直式自动化集装箱码头布局．该码头划分为岸桥作业区、AGV作业区和自动化堆场作业区，共建设A、B两座换电站，并分布在码头两端．换电站A为小换电站，配置1个换电工位；换电站B为大换电站，配置2个换电工位，即可以同时为2台AGV更换电池包，每个换电工位完成1次电池包更换平均花费300 s．

(a) 非接触式充电

(b) 换电式

从AGV电量消耗的角度考虑，将AGV划分为3种状态(表1)，每种状态下耗电量和行驶速度均不同：在停车状态下，耗电量最小，仅维持AGV导航、通信等系统的正常运行；在重载状态下，耗电量最大，AGV运载集装箱由发箱位置到收箱位置；在空载状态下，耗电量适中，AGV正常空驶．3种状态下的AGV分别对应8种不同工作场景，见图2．场景a为AGV在AGV等待区，等待接收指令；场景b为AGV等待岸桥完成作业；场景c为AGV等待场桥完成操作；场景d为AGV在换电站排队等待更换电池包；场景e为装船作业，AGV在堆场装箱行驶至岸边卸箱；场景f为卸船作业，AGV在岸边装箱行驶至堆场卸箱；场景g为AGV由收箱位置行驶至发箱位置；场景h为AGV驶向换电站和驶离换电站．

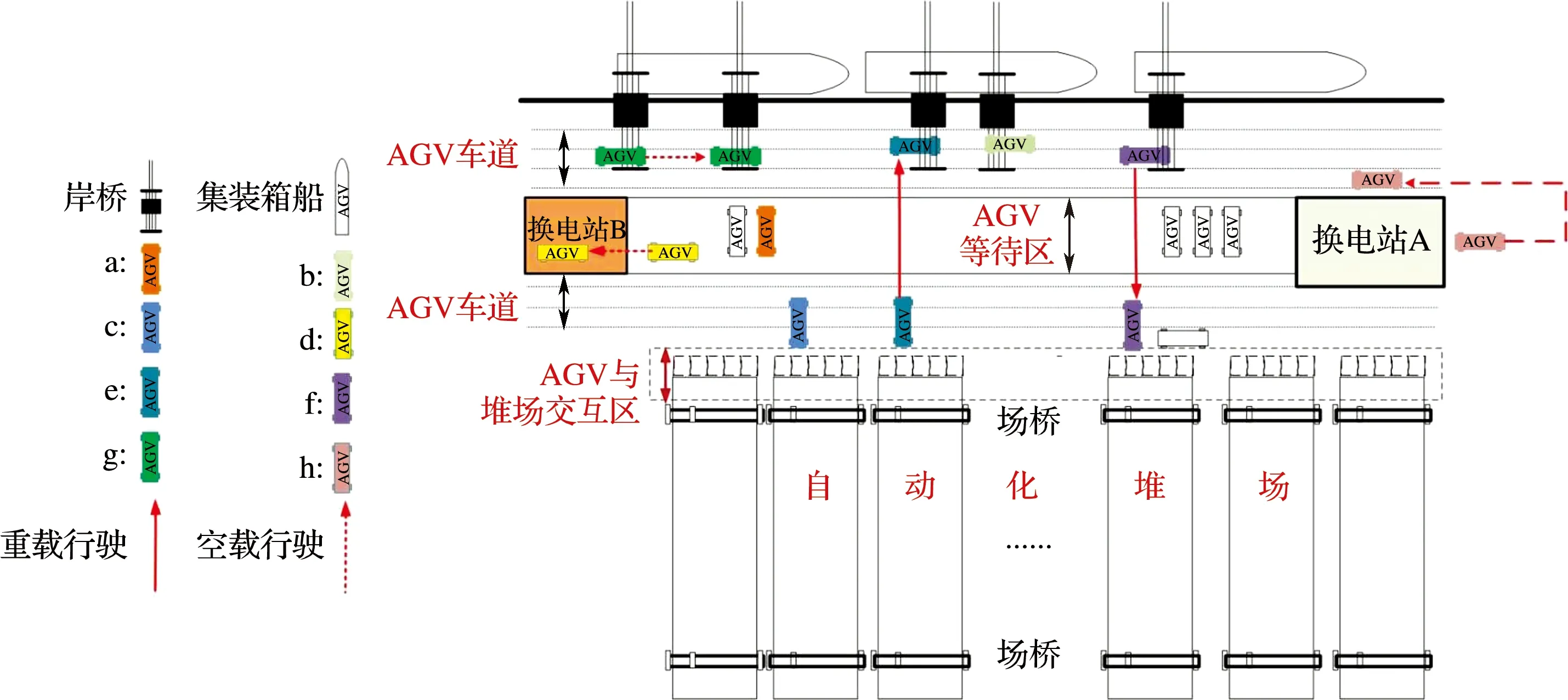
图2 洋山四期自动化码头Fig.2 Yangshan Phase Ⅳ automated terminal

表1 AGV状态划分Tab.1 AGV status division

每台AGV的作业状态均在8种场景中不断地变换，电量在不停地更新．为了尽量减少因AGV断电停止作业带来的损失，结合实地调研结果，本文采用固定阈值换电策略，具体如下：每台AGV初始电量均为100%，在接收作业指令时，判断AGV剩余电量是否大于换电阈值，当且仅当AGV剩余电量不大于换电阈值时，不再接收任何作业指令，前往换电站更换电池包．AGV在更换完电池包之后再次投入使用，直至全部作业任务完成．AGV换电总时间为各台AGV驶向和驶离换电站的时间、换电站排队时间以及电池包更换操作时间总和，具体换电过程分析如图3所示．

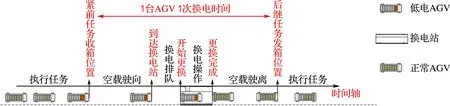
图3 AGV换电过程分析Fig.3 Analysis of AGV battery exchange process

AGV调度决定了AGV何时换电，AGV换电过程决定了AGV何时再次投入使用，彼此相互联系，从而影响AGV任务的最终完工时间．本文根据AGV调度和换电之间的关系，建立AGV调度和换电的双层耦合模型，如图4所示．在图中，上层模型为AGV调度模型，以最终完工时间最小化为目标，决策AGV调度；下层模型为AGV换电模型，以换电总时间最小化为目标，决策每台AGV每次选择的换电站．

具体如下：AGV调度模型中考虑换电电量约束，设定每台AGV最大允许换电次数和换电任务，每次任务结束时判断剩余电量是否低于换电阈值，若是则执行换电任务即前往指定换电站编号，否则接收并执行下一任务，直至全部任务完成，以最终完工时间最小化为目标决策制定AGV调度方案和AGV换电需求，即每台AGV任务作业顺序、每次换电时间、换电紧前任务、换电后继任务和换电时刻剩余电量，为AGV换电模型提供输入数据．

图4 双层耦合模型框架Fig.4 Two-layer coupling model frame

AGV换电模型中考虑AGV换电需求、换电站位置、换电站工位数量和先到先服务原则等约束，以换电总时间最小化为目标决策制定AGV换电方案，即每台AGV每次换电所选换电站编号和相应的排队时间，对应调度模型中换电任务编号和等待时间．以换电需求和换电方案连接两个子模型，并通过迭代不断更新公共设计变量，形成两个模型的双层耦合关系．

2 模型建立

2.1 AGV调度模型(上层模型)

2.1.1 模型假设 AGV初始电量均为100%；在作业过程中，AGV不会晚于计划时间到达指定位置；在作业过程中，不考虑设备故障以及碰撞；岸桥、场桥的每个装卸任务的操作顺序和操作时间已知；所有集装箱大小均为12.192 m，1辆AGV 1次装载1个集装箱；不考虑码头突发状况和AGV冲突因素．

2.1.2 符号说明

(1)集合

V0：V0={v0}，虚拟开始任务集合；

V′0：V′0={v′0}，虚拟结束任务集合；

Vt：Vt={1，2，…，t}，装卸任务集合；

K：K={1，2，…，k}，AGV集合；

Vk：Vk={1，2，…，n}，第k台AGV对应的换电任务；

Vb：Vb=V1∪V2∪…∪Vk，全部换电任务集合；

V：V=V0∪V′0∪Vb∪Vt，任务集合．

(2)参数

s1、s2：AGV空载和重载速度；

r1、r2、r3：AGV空载、重载和停车每秒耗电率；

C：换电阈值(安全电量)；

y：岸桥的平均操作时间；

q：场桥的平均操作时间；

M：一个无穷大的正数；

afix：一次更换电池包的操作时间；

Wki：第k台AGV执行换电任务i的排队时间；

di：任务i发箱位置与收箱位置的距离；

ei：任务i的最早允许作业时间；

Dij：任务i收箱位置与任务j发箱位置的距离，换电任务收箱位置和发箱位置均转化为换电站位置；

dki：第k台AGV执行任务i的空驶距离，从紧前任务收箱位置到任务i发箱位置的距离；

zki：第k台AGV执行任务i的完成时间；

wki：第k台AGV执行任务i的岸边等待时间；

bki：第k台AGV开始任务i的电池包剩余电量；

Bki：第k台AGV完成任务i的电池包剩余电量．

(3)决策变量

xkij为0-1变量，若第k台AGV在执行任务i之后紧接着执行任务j，则xkij=1，否则xkij=0．

2.1.3 AGV调度模型建立 在本模型中，根据装卸任务量、每个任务的最早允许作业时间、每台AGV最多允许换电次数和AGV数量，建立以AGV最终完工时间最小化为目标的AGV调度模型．

目标函数：

minF

约束条件：

F≥zki；∀k∈K，i∈V

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

wkj≥ej-zki-dki/s1+(xkij-1)M；

∀k∈K，j∈Vt，i∈V

(9)

zkj≥zki+wkj+dkj/s1+dkj/s2+y+q-

(1-xkij)M； ∀k∈K，j∈Vt，i∈V

(10)

zkj≥zki+wki+afix+dki/s2+(1-xkij)M；

∀k∈K，j∈Vk，i∈Vt

(11)

bkj=Bki+(1-xkij)M；

∀k∈K，i∈V，j∈Vt

(12)

bkj≤C；∀k∈K，j∈Vb

(13)

Bki=100；∀k∈K，i∈V0∪Vb

(14)

Bki=bki-r1dki/s1-r2di/s2-r3wki；

∀k∈K，i∈Vt

(15)

(16)

(17)

∀k∈K，i，j∈Vk，j≤i

(18)

zki>0，Bki>0，wki≥0，dki≥0；

∀k∈K，i∈V

(19)

目标函数：最终完工时间最小化．

完工时间约束：式(1)任务完成时间不小于任意任务的完成时间．

任务约束：式(2)、(3)为每台AGV必须完成虚拟开始和虚拟结束任务；式(4)、(5)为每个任务仅有一个紧前和后继任务，且允许换电任务不必全部完成，即无须每台AGV都发生n次换电；式(6)为平衡约束，中间任务必须运输平衡，即输入等于输出．

距离约束：式(7)为AGV执行任务空驶距离．

时间约束：式(8)、(9)为等待时间，虚拟等待时间为0，换电任务等待时间为换电时间，普通任务等待时间由到达发箱位置的时间和最早允许作业时间计算得到；式(10)、(11)为任务完成时间，普通任务完成时间由紧前任务完成时间、等待时间、岸桥操作时间、场桥操作时间、空驶时间和重驶时间求和得到，换电任务完成时间由紧前任务完成时间、换电操作时间、空载驶向换电站时间、等待时间求和得到．

电量约束：式(12)为接受任务时AGV剩余电量，接受普通作业任务时即紧前任务完成时剩余电量；式(13)为接受换电任务时，AGV剩余电量不大于换电阈值；式(14)、(15)为AGV完成任务时剩余电量，普通任务计算方式为接收任务时电量、重载耗电量、空载耗电量计算而得，换电任务完成时电量为100%，即AGV更换新电池包．

换电任务约束：式(16)表示AGV只能执行独自所属n个虚拟换电任务；式(17)为1台AGV的换电次数之和，不允许超过最多换电次数n；式(18)为1台AGV的换电任务只能按照所属换电任务编号从小到大依次执行，即若换电i次，只能完成前i个换电任务，不能完成多余的换电任务．

变量约束：式(19)为变量的约束条件．

2.2 AGV换电模型(下层模型)

2.2.1 模型假设 每个换电站内可用电池包的数量充足；每个换电站遵循先到先服务规则；不考虑换电工位维护等不确定性因素；每个换电工位同一时刻仅为1台AGV更换电池包；每个换电站配置1个换电工位．

2.2.2 符号说明

(1)集合

T：T={1，2，…，m}，换电站集合；

Uk：换电需求集合，由调度模型可得，u∈U，U=U1∪U2∪…∪Uk．

(2)参数

Buk：第k台AGV第u次换电指令产生时的剩余电量；

Suk：第k台AGV第u次换电指令产生时间；

dukm：第k台AGV第u次换电驶向换电站m的距离；

Dukm：第k台AGV第u次换电选择m号换电站与后继任务发箱位置距离；

fuk：第k台AGV完成第u次换电后，到达换电后继任务发箱位置时间；

Aukm：第k台AGV第u次换电选择m号换电站的到达时间；

Cukm：第k台AGV第u次换电选择m号换电站的开始操作时间；

Wukm：第k台AGV第u次换电选择m号换电站的排队时间；

Lukm：第k台AGV第u次换电选择m号换电站的完成时间．

(3)决策变量

ykk′m：0-1变量，第k台AGV比第k′台AGV提前到达m号换电站，则ykk′m=1，否则ykk′m=0；

pukm：0-1变量，若第k台AGV第u次换电选择m号换电站，则pukm=1，否则pukm=0．

2.2.3 AGV换电模型建立 在本模型中，考虑换电站的位置、排队时间和电量消耗差异，建立以AGV换电总时间最小化为目标的AGV换电模型．

目标函数：

minF′

约束条件：

(20)

(21)

(22)

(23)

fuk≥Lukm+Dukm/s2+(pukm-1)M；

∀u∈Uk，k∈K，m∈T

(24)

Aukm≥(pukm-1)M+Suk+dukm/s2；

∀u∈Uk，m∈T，k∈K

(25)

∀m∈T，k，k′∈K，u∈Uk′，u′∈Uk′

(26)

Cukm≤(1-pukm)M+Aukm+Wukm；

∀u∈Uk，m∈T，k∈K

(27)

Lukm≤(1-pukm)M+Cukm+afix；

∀u∈Uk，m∈T，k∈K

(28)

(1-pukm)M+Buk-r2dukm/s2-r3Wukm≥0；

∀u∈Uk，k∈K，m∈T

(29)

(1-ykk′m)M+Aukm-Au′k′m≥0；

∀m∈T，k，k′∈K，u∈Uk，u′∈Uk′

(30)

ykkm=0；∀m∈T，k∈K

(31)

fuk>0，Wukm≥0； ∀m∈T，k，k′∈K，u∈U

(32)

目标函数：最小化AGV换电总时间．式(20)为AGV换电总时间的计算．

排队约束：式(21)为1台AGV每次换电只能选择1个换电站；式(22)、(23)为AGV在换电时前后最多各有1台AGV需要被服务；式(30)为2台AGV存在前后排队关系前提是前者比后者提前到达同1个换电站；式(31)排除不可能产生排队现象，即连续被同1个换电站服务的AGV编号不可能相同．

时间约束：式(24)为到达后继任务发箱位置时间，即该次换电的完成时间与空载驶离时间之和；式(25)为到达换电站时间，即该次换电指令产生时间与空载驶向换电站时间之和；式(26)为换电站排队时间，若到达换电站时前1台AGV尚未完成换电则等待，否则无须等待；式(27)为换电工位开始操作时间，即到达换电站时间与排队时间之和；式(28)为更换电池操作完成时间，即操作开始时间加上换电操作时间．

电量约束：式(29)为电量必须足够到达所选换电站．

变量约束：式(32)表示时间变量非负．

3 算法设计

3.1 循环迭代流程

依据上述建模思路，提出循环迭代求解算法，分别求解AGV调度模型(上层模型)和AGV换电模型(下层模型)．将调度模型和换电模型多次循环迭代计算，不断更新公用变量的值，实现AGV调度方案的最优，具体流程如图5所示．

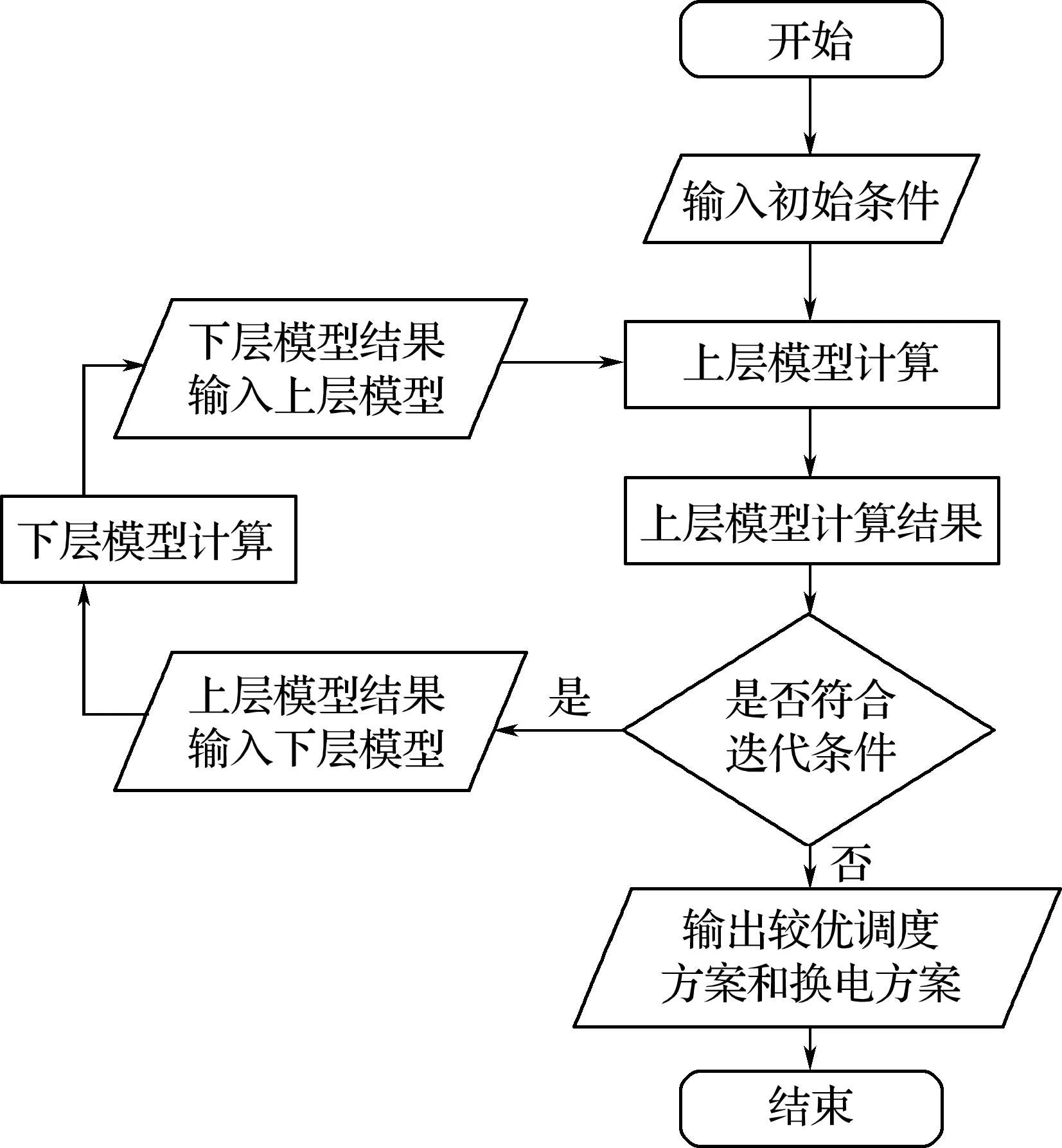
图5 迭代计算流程Fig.5 Iterative calculation process

在图5初始条件下，设定初始换电任务的位置(换电站编号)和换电排队时间，通过AGV调度模型，可得AGV作业任务顺序，即AGV调度方案．同时，可得换电任务的紧前任务、后继任务、相应电量和接受任务时间，进而可知每台AGV每次换电驶向和驶离各个换电站的距离、指令产生时间和剩余电量．将空驶距离矩阵、换电产生时间和剩余电量作为已知条件代入AGV换电模型，求解可得不同AGV换电时所选的不同换电站编号和排队等待时间，依据换电方案更新AGV调度模型中的换电任务位置和等待时间，如此循环迭代求解，直至最终完工时间不发生变化或迭代到一定次数，输出较优的AGV调度方案和换电方案．

3.2 AGV调度模型(上层模型)遗传算法设计

遗传算法(GA)是求解NP-hard问题的经典算法之一，其编码规则简单有效，具有高度并发性和全局搜索能力，因此广泛用于求解AGV调度模型，以获得其近似最优解．

(1)染色体编码：整数编码方式，染色体长度为任务数和虚拟任务数之和，第i个位置的编号k表示第i个任务由第k台AGV完成，如图6所示．10个任务由3台AGV分配完成，假设每台AGV最多需要换电2次，任务11～16为虚拟换电任务；任务11和12对应第1台AGV所属换电任务，任务13和14对应第2台AGV所属换电任务，任务15和16对应第3台AGV所属换电任务．虚拟换电任务不必一定执行，若第1台AGV仅换电1次，则虚拟换电任务仅完成任务11；若第1台AGV换电2次，则必须完成任务11和12；若第1台AGV无须换电，则任务11和12均无须完成．

图6 上层模型染色体编码Fig.6 Chromosome coding of the upper model

(2)适应度函数：取AGV调度模型目标函数的倒数作为适应度值，即1/F．

(3)选择：轮盘赌选择．

(4)交叉：两点交叉，设置交叉概率Pc1，将被交叉概率选中的染色体作为父代1和父代2，在任务编码部分随机生成两个交叉点位，两点之间的染色体部分即为交叉部分R1、R2，AGV换电任务部分保持不变．

(5)变异：交换变异，设置变异概率Pm1，在染色体的任务部分随机选择两个基因值M1和M2进行交换，改变AGV作业顺序，换电任务编号保持不变．

3.3 AGV换电模型(下层模型)遗传算法设计

鉴于AGV换电模型中存在非线性约束关系，遗传算法编码规则简单且遗传操作比其他算法种群操作产生非法解的概率更低，因此采用遗传算法求解AGV换电模型．

(1)染色体编码：采用矩阵整数编码方式，由AGV调度模型的结果可知每台AGV执行换电任务的次数，即每台AGV换电次数，第k行第n列的位置表示第k台AGV第n次换电选择的换电站编号．如图7所示，3台AGV，每台AGV最多需要换电2次，第1台AGV需要换电2次，第1次换电选择1号换电站，第2次换电选择2号换电站；第2台AGV仅换电1次，选择1号换电站；第3台AGV需要换电2次，每次都选择2号换电站．

图7 下层模型染色体编码Fig.7 Chromosome coding of the lower model

(2)适应度函数：取AGV换电模型目标函数的倒数为适应度值，即1/F′．

(3)选择：轮盘赌选择．

(4)交叉：设置交叉概率Pc2，随机选择两行基因值p1和p2进行交换得到新的染色体．将被交叉概率选中的染色体作为父代1和父代2，随机生成两个交叉点位，交叉得到两条新染色体．

(5)变异：设置变异概率Pm2，每条染色体每行随机选择一个点位，重新生成基因值．

(6)染色体修复：在经历选择、交叉、变异之后，种群中存在不符合条件的染色体，如图8(a)所示，第2台AGV必须换电1次，第3台AGV必须换电2次，则进行染色体修复．将第2行第2列基因值赋值为0，第3行第1列赋值为1或2．

(a) 修复前(b) 修复后图8 下层模型染色体修复Fig.8 Chromosome repair of the lower model

4 算例分析

4.1 参数与环境

本文针对以上所建立的模型和方法，设计了小规模算例和大规模算例．对于小规模算例，采用GAMS数学规划软件调用SBB求解器分别求得AGV调度模型和换电模型精确解，最终迭代得到双层模型最优解．之后对大规模算例采用遗传算法进行循环迭代求解，并分析不同规模下算法的有效性和参数的影响．

以上海港洋山四期自动化码头实际布局为基础，适当修正换电站、岸桥和场桥之间的行驶距离，如表2所示．每台岸桥执行1次任务平均花费120 s；场桥内每台场桥执行1次任务平均花费90 s；混合装卸作业模式，1台AGV完成1次电池包更换动作平均花费300 s．

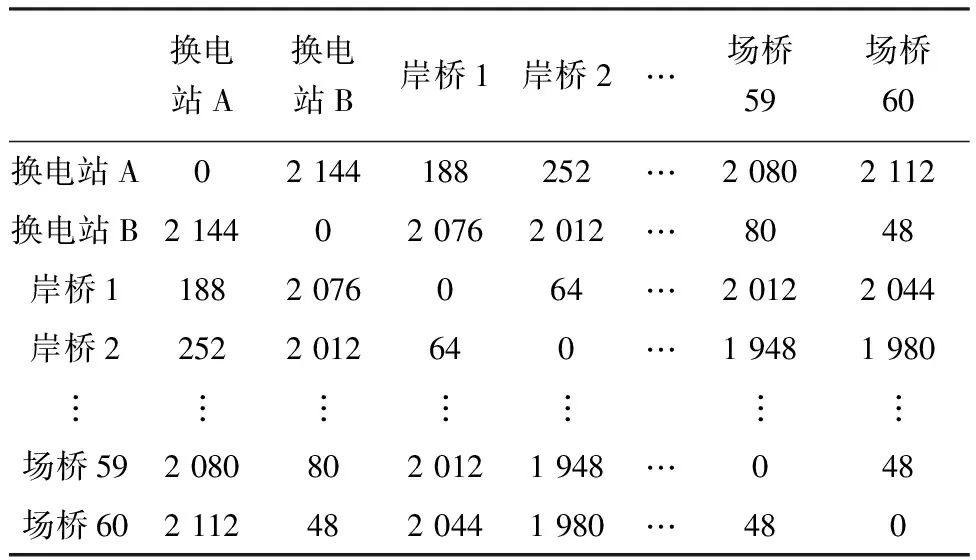
表2 换电站-岸桥-场桥的距离矩阵Tab.2 Distance matrix of battery exchange station-quay crane-yard m

4.2 小规模算例

鉴于任务较少时，AGV无须换电，而任务较多时，求解器无法完成求解，为验证模型的有效性，如表3所示，在码头实际参数基础上缩小空载速度、重载速度和耗电率等参数，空载耗电率为0.1%/s，AGV重载耗电率为0.2%/s，AGV停车时耗电率为0.05%/s，共设2个换电站(各配1个换电工位)．

表3 小规模算例参数Tab.3 Small-scale calculation example parameters

设定最大循环次数为50，AGV调度部分，种群大小为20，交叉概率为0.8，变异概率为0.1；AGV换电部分，种群大小为10，交叉概率为0.7，变异概率为0.15，最长求解时间为1 h．

设置3组不同实验，分别通过GAMS和GA迭代求解，结果见表4．第1组和第2组GAMS结果与GA上层目标结果几乎相同，说明了GA的有效性．当任务数量增多时，GAMS无法在1 h内得出结果，而GA仍可以求解，说明本文提出的算法在求解较多任务时存在一定的优势．

表4 小规模算例求解结果Tab.4 Small-scale calculation example solution results

以20个任务、4台AGV为例，GA得到的AGV作业任务序列如图9所示，说明其可以有效地决策AGV选择换电站，合理控制换电总时间，且每台AGV分配的任务数量较平均，对自动化集装箱码头AGV调度有一定的应用价值．

4.3 大规模算例

为验证本文算法在码头实际作业情况下的表现效果，结合码头实际运营参数设立AGV空载耗电率为0.01%/s，AGV重载耗电率为0.02%/s，AGV停车时耗电率为0.005%/s，共设2个换电站，换电站A设置1个换电工位，换电站B设置2个换电工位，并将换电站B抽象为2个位置相同的换电站B1和B2，各配置1个换电工位，结合电池耗电特点建立AGV速度与电池剩余电量分段函数关系，见表5．

图9 AGV调度甘特图Fig.9 AGV scheduling Gantt chart

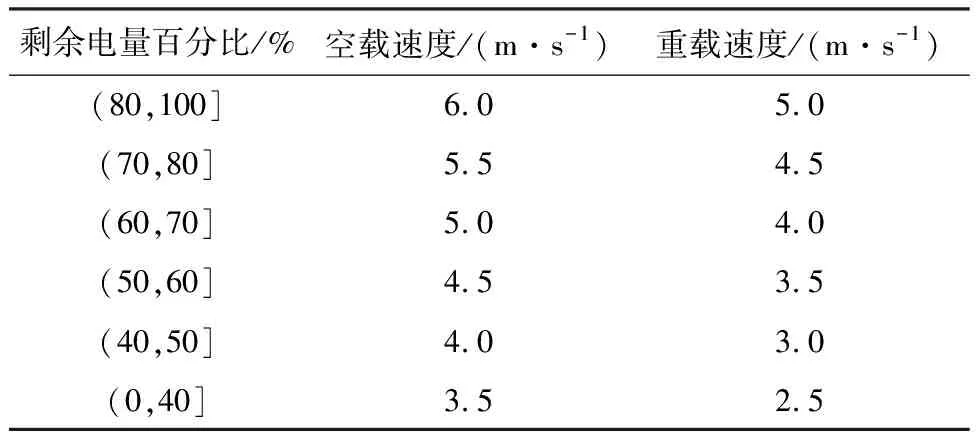
表5 大规模算例参数Tab.5 Large-scale calculation example parameters

首先，随机生成500个任务，配置10台AGV，换电阈值为35%，使用遗传算法求解，设定最大循环次数为1 000．AGV调度部分，种群大小为100，交叉概率为0.7，变异概率为0.1，最大遗传代数为300；AGV换电部分，种群大小为50，交叉概率为0.7，变异概率为0.15，最大遗传代数为50．求得的AGV调度最终完工时间为14 819 s，换电总时间为8 056 s，换电总次数为10．具体AGV换电站信息见表6．分析500个任务下的换电站信息可知，每次AGV换电空驶距离差异显著，AGV换电排队时间均小于240 s，有效避免了换电站排队拥堵现象，合理选择了AGV换电站，进而提升AGV利用率．

其次，扩大算例规模，分析AGV数量对最终完工时间和换电总时间的影响．观察不同规模下的算例结果(表7)可知，在同一任务数量下，AGV数量增多最终完工时间会明显降低，AGV换电总次数不会发生较大变化，但换电总时间会随之增加，即AGV空驶时间和换电排队时间增加，码头的运营成本增加．为此，码头实际运营过程中不可

表6 大规模算例的换电站信息Tab.6 Battery exchange station information forlarge-scale calculation examples

表7 不同规模算例的结果Tab.7 Results of different scale examples

一味追求增加AGV数量从而缩短完工时间，必须综合考虑数量增多导致可能出现的换电问题．

4.4 算法比较

本文在大规模算例下，设计6组实验，每组实验用GA与PSO算法进行求解，并对求解结果进行对比．表8为不同算例规模下GA和PSO的求解结果，每组实验每个算法分别运算3次，取平均值为最终结果．

分析实验1～4可知，当AGV和任务数量较少时，GA结果略优于PSO，GA运行时间优于PSO．实验5、6结果表明，随着算例规模的增大，无论是完工时间还是运行时间，GA都明显优于PSO，由此验证了GA在求解本文AGV调度与换电双层耦合模型的算法优势．

表8 不同算法结果对比Tab.8 Result comparison of different algorithms

5 结 语

本文从自动化集装箱码头实际换电站数量和位置出发，建立了AGV调度和换电的双层耦合模型，分别采用GAMS求解器和遗传算法循环迭代求解实际作业设计算例．在小规模算例下，GAMS求解器和遗传算法的求解结果基本一致，证明了双层耦合模型和遗传算法的有效性．在大规模算例下，以500个任务10台AGV为例，AGV换电站排队最长时间小于240 s，平均排队时间为90 s，证实该方案有效缓解了AGV换电站排队拥挤情况，提升了AGV利用率．通过对比不同大规模算例可知，码头实际运营过程必须考虑AGV数量配置导致的可能出现的换电排队问题．同时，遗传算法和粒子群算法结果对比分析验证了本文算法的优势．

本文所建立双层耦合模型对于自动化集装箱码头AGV换电具有指导意义，对于电动汽车和无人机的充换电问题有一定的参考意义．但是，本文尚未考虑换电站电池包数量、电池寿命等因素的影响，日后研究可逐步考虑此类因素．同时，可以继续深入研究其他多种形式的自动化集装箱码头布局、换电站选址优化、换电站工位配置与AGV换电的关系．