扩张李代数Schrödinger-Virasoro子代数生成元和一些李子代数幂零性

余 德 民， 柴 嘉 潞， 李 笛， 罗 德 仁， 吴 伟 才， 蒋 婵

( 湖南理工学院 数学学院， 湖南 岳阳 414000 )

0 引 言

本文研究扩张李代数Schrödinger-Virasoro．这类李代数在数学和理论物理中尤其是共形理论和弦论中有非常重要的应用．

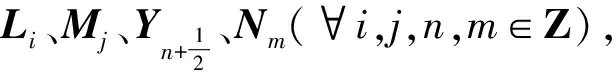
[Lm，Ln]=(n-m)Ln+m

[Lm，Mn]=nMn+m

[Mm，Mn]=0

[Lm，Nn]=nNn+m

[Mm，Nn]=-2Mn+m

[Nm，Nn]=0

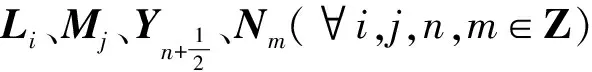
1 主要结果

定义1设由Li(∀i∈Z)张成的子空间为h1．设L2、L-3生成的李代数记为[[L2，L-3]]．

由于

[L2，L-3]=-5L-1

[L2，L-1]=-3L1

[L-3，L1]=4L-2

[L-1，L1]=2L0

故L-3，L-2，L-1，L0，L1，L2∈[[L2，L-3]]．

稍作分析可得，L-3、L-2、L-1、L0、L1、L2能够生成李代数h1，h1的最小生成元为2．

现在来考察3个自然基向量L6、L10、L-15，由于6、10、-15两两不互素，从而L6、L10、L-15任意两个自然基向量不能生成李代数h1，但

[L6，L10]=4L16

[L16，L-15]=-31L1

稍作分析可得，3个自然基向量L6、L10、L-15能生成李代数h1．同理另外考察3个自然基向量L6、L14、L-21，由于6、14、-21两两不互素，从而L6、L14、L-21任意两个自然基向量不能生成李代数h1，但

[L6，L14]=8L20

[L20，L-21]=-41L-1

稍作分析可得，3个自然基向量L6、L14、L-21能生成李代数h1．

定理1设3个自然基向量Li、Lj、Lm(∀i，j，m∈Z)能够生成李代数h1，则L-i、L-j、L-m也能够生成李代数h1．

证明构造满足h1到h1的线性映射如下：

φ01：φ01(Li)=-L-i， ∀i∈Z

φ01([Li，Lj])=[φ01(Li)，φ01(Lj)]，∀i，j∈Z

φ01是h1到h1的同构．Li、Lj、Lm(∀i，j，m∈Z)能够生成李代数h1，由于

φ01(Li)=-L-i

φ01(Lj)=-L-j

φ01(Lm)=-L-m

则L-i、L-j、L-m(∀i，j，m∈Z)能够生成李代数h1．

□

设由L0，L-2，L-4，L-6，…，L-2n，L-2n-2，L-2n-4，…张成的子空间为h12．h12也为g的李子代数．对任意L2m、L2n，∀m≤0，n≤0，m∈Z，n∈Z不能李生成h12，用定理表述如下．

定理2∀m≤0，m∈Z，n≤0，n∈Z，L2m、L2n不能李生成h12．

证明采用反证法，设L2m、L2n，∀m<0，n<0，n∈Z，m∈Z能李生成h12．由于

[L2m，L2n]=2(n-m)L2(n+m)；m<0，n<0，n+m<0

必有

L0∉[[L2m，L2n]]

从而m、n必有一个为0，假设m、n其中有一个为0，不妨假设n=0，则由于

[L0，L2m]=2mL2m

显然

L2m-2∉[[L2m，L0]]

从而矛盾．假设m、n都为0，则由于

[L0，L0]=0

显然

L-2∉[[L0，L0]]

从而矛盾．

□

定理3∀m≤0，m∈Z，n≤0，n∈Z，k≤0，k∈Z，L2m、L2n、L2k能李生成h12，则{2m，2n，2k}={0，-2，-4}．

证明由于m、n、k都是非正整数，显然m、n、k必有一个等于0，否则

L0∉[[L2m，L2n，L2k]]

不妨设m=0，2n、2k必有一个等于-2，否则

L-2∉[[L0，L2n，L2k]]

不妨设2n=-2，2k必等于-4，否则

L-4∉[[L0，L-2，L2k]]

从而{2m，2n，2k}={0，-2，-4}，进一步可以证明L0、L-2、L-4确实能够李生成h12．

□

设由Mi(∀i∈Z)张成的子空间为h2，h2是g的无限维交换子代数．

定理4h2无有限生成元．

证明采用反证法，设x1，x2，…，xn为其有限生成元，∀i，j∈Z，

[Mi，Mj]=0

从而∀i，j∈Z，

[xi，xj]=0

h2是无限维李代数，从而必存在x，使得x不能被x1，x2，…，xn线性表示，即x≠k1x1+k2x2+…+knxn，原命题成立．

□

设由Li、Mj(∀i，j∈Z)张成的子空间为h4，h4是g的无限维非交换子代数．

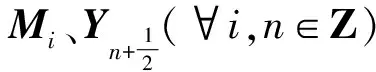
定理5h5无有限生成元．

证明采用反证法，设y1，y2，…，yn为其有限生成元，由于

[Mm，Mn]=0

不妨设

yi=yi1+yi2；yi1∈h2，yi2∈h6

[yi，yj]=[yi1+yi2，yj1+yj2]=

[yi2，yj2]∈h2

而h6是无限维线性空间，从而必存在y，使得y不能被y1，y2，…，yn线性表示，即y≠k1y12+k2y22+…+knyn2．则y无法由y1，y2，…，yn李运算生成，从而原命题成立．

□

则h5/h2也是李代数．

定理6商李代数h5/h2无有限生成元．

证明

由于

商李代数h5/h2为交换李代数，商李代数h5/h2为无限维交换李代数．商李代数h5/h2无有限生成元．

□

定理7h5为幂零李代数．

证明h5的李运算如下：

由于

[Mm，Mn]=0

不妨设

yi=yi1+yi2；yi1∈h2，yi2∈h6

由于

[yi，yj]=[yi1+yi2，yj1+yj2]=

[yi2，yj2]∈h2

从而

又由于

从而h5为幂零李代数．

□

定理8g有有限生成元．g的生成元可为5．

证明g的李运算如下：

[Lm，Ln]=(n-m)Ln+m

[Lm，Mn]=nMn+m

[Mm，Mn]=0

可知L2、L-3能够生成h1，因为

[L-2+i，M2]=2Mi

[L-2+i，N2]=2Ni

若i≠7

若i=7，由于

则

若

□

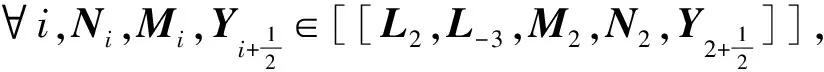
定理9g不为可解李代数．

证明方法1：g的李运算如下：

[Lm，Ln]=(n-m)Ln+m

[Lm，Mn]=nMn+m

[Mm，Mn]=0

[Lm，Nn]=nNn+m

[Mm，Nn]=-2Mn+m

[Nm，Nn]=0

由于

[L0，L6]=6L6

从而

L6∈[g，g]

由于

[L0，L-15]=-15L-15

从而

L-15∈[g，g]

由于

[L0，L10]=10L10

从而

L10∈[g，g]

[L6，L10]=4L16

[L-15，L16]=31L1

进而

L1∈[g，g]

[L0，N2]=2N2

从而

N2∈[g，g]

由于

[L0，M2]=2M2

从而

M2∈[g，g]

由于

从而

进而有

g(1)=[g，g]=g

g(2)=[g(1)，g(1)]=g

g(3)=[g(2)，g(2)]=g

∀k∈Z+，g(k+1)=[g(k)，g(k)]=g

从而g不为可解李代数．

方法2：先证h1不可解

由于

[L2，L4]=L6

[L3，L7]=4L10

[L-12，L-3]=9L-15

则L6，L10，L-15∈[h1，h1]，而L6、L10、L-15能够生成h1，故

h1=[h1，h1]

又

从而h1不可解．

反证，如果g可解，则h1也可解，出现矛盾．

□

2 结 语

本文研究了扩张Schrödinger-Virasoro李代数的有限生成元、李代数的幂零和可解等结构问题．可以进一步研究这类李代数的中心和理想，及其全部自同构以及自同构群等结构问题．并可继续研究扩张Schrödinger-Virasoro李代数的表示．