广义彼得森图意大利控制数
2021-11-29高红,黄佳欢,尹亚男,杨元生
高 红, 黄 佳 欢, 尹 亚 男, 杨 元 生
( 1.大连海事大学 理学院, 辽宁 大连 116026;2.大连理工大学 计算机科学与技术学院, 辽宁 大连 116024 )
0 引 言
图的罗马控制[1]起源于古罗马帝国的军事防御问题[2].公元4世纪,君士坦丁大帝为了保障帝国的安全在军团数量十分有限的情况下制定了部署和调动军队的规则:(1)每个地区最多能部署两组军团.(2)一个地区如果没有驻军,在其受到外来侵略时,相邻地区必须能派出援军.(3)一个地区必须拥有两组军团才能派出一组军团去支援相邻地区.如果一个地区部署0/1/2组军团,那么可以看成是将该点赋值为0/1/2.如果古罗马帝国(图G)中每个地区(顶点)都对应着一个数字——0、1或者2,于是,军队的部署方案可以看成是从图G的顶点集合V到{0,1,2}的映射f,即f:V→{0,1,2}.根据部署规则,所有函数值为0的顶点其邻域中至少有一个函数值为2的顶点,函数f称为图G上的罗马控制函数.图G中所有顶点函数值的总和称为f的权重.罗马控制函数权重的最小值称为图G的罗马控制数,记为γR(G).确定图的罗马控制数已成为学者们关注的热点问题.
意大利控制[3]是罗马控制的一种推广,其定义如下.

图的意大利控制也被称为罗马{2}-控制[4]或弱{2}-控制[5].确定图的意大利控制数是NP困难的,吸引了国内外很多研究者的关注.文献[3]研究了树图T的意大利控制数与经典控制数之间的关系.文献[6]研究了树图的意大利控制数,证明了树图意大利控制数与其2-彩虹控制数相等.文献[5]确定了圈与圈的笛卡儿乘积图Cn□C3和Cn□C4的意大利控制数.文献[7]确定了Cn□C5的意大利控制数.文献[8]确定了广义彼得森图P(n,3)的意大利控制数.文献[9-12]研究了图的全局意大利控制数、独立意大利控制数、外独立意大利控制数和完美意大利控制数.
本文研究广义彼得森图P(n,k)(k≥4)的意大利控制数.首先,根据广义彼得森图的特点构造意大利控制函数.利用这些函数计算得到广义彼得森图P(n,k)(k≥4)的意大利控制数的上界.然后,结合前人给出的意大利控制数的下界,确定当k≡2,3(mod 5)且n≡0(mod 5)时,P(n,k)(k≥4)意大利控制数的精确值.
1 广义彼得森图
广义彼得森图P(n,k)是一个有2n个顶点的3-正则图,其顶点集合和边的集合分别为
V(P(n,k))={vi|0≤i≤2n-1},
E(P(n,k))={(vi,vi+1),(vi,vi+2)|0≤i≤2n-1且i≡0(mod 2),下标对2n取模}∪
{(vi,vi+2k)|0≤i≤2n-1且i≡1(mod 2),下标对2n取模}
图1(a)显示的是彼得森图P(9,4).为了便于表示彼得森图的意大利控制函数,本文将P(n,k)沿v0和v2n-2之间的半径剪开,如图1(b)所示.

(a) P(9,4)
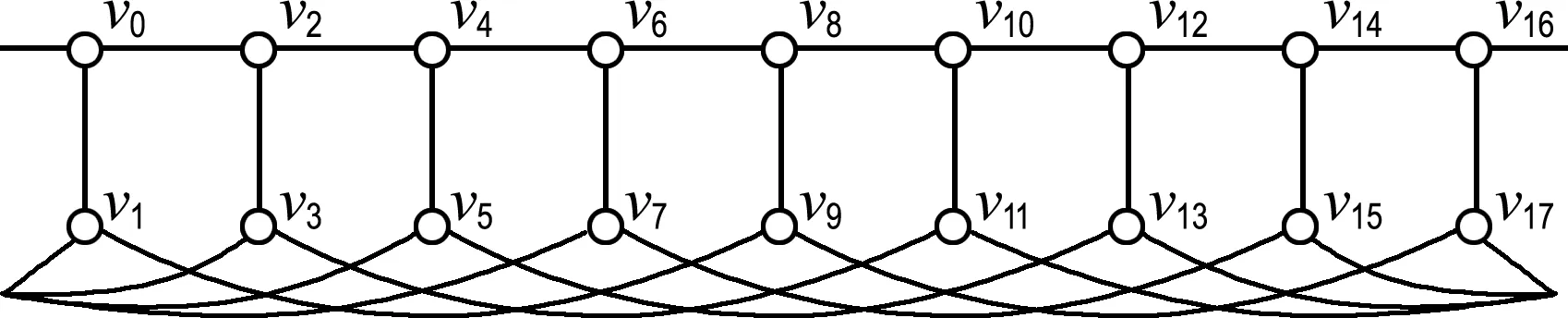
(b) 剪开的P(9,4)
设f为广义彼得森图G上的意大利控制函数,则用下面的形式表示f:
例如,

表示P(9,4)上的意大利控制函数,其图形如图2所示.

图2 彼得森图P(9,4)上的意大利控制函数Fig.2 Italian domination function on Petersengraph P(9,4)
2 P(n,k)(k≥4)意大利控制数
2.1 P(n,k)(k≥4)意大利控制数的下界
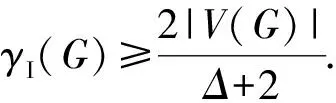
P(n,k)是3-正则图,所以Δ(P(n,k))=3,并且|V(G)|=2n,故由定理1可以得到推论1.
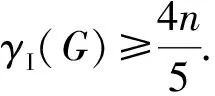
2.2 P(n,k)(k≥4)意大利控制数的上界
定理2若G=P(n,k)(k≥4),则
证明
情况1k≡0(mod 5).首先定义一个彼得森图上的函数g:
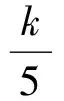
情况1.1当n≡0(mod 5k)时,构造P(n,k)上的意大利控制函数f如下:

f(vi)=g(vi mod 10k)
此时,f的权重为

情况1.2当n≢0(mod 5k)时,构造P(n,k)上的意大利控制函数f如下:
其中
(1)
h还可以表示为下面更直观的形式:
此时,f的权重为
乡村客栈和家庭旅馆的建设也表现出不同的风格和个性。乡村的住宿风格不仅有常见的形式,还包括磨坊客栈(Moulin Etape)和葡萄园旅舍(Grandes Etapes des Vignobles)等。法国所有的乡村客栈和家庭旅馆都会呈现出不同地区的浓厚地域文化风情,具有乡居情怀,让过夜的旅客可以更好地融入本地的自然风俗生活中。
w(f)=
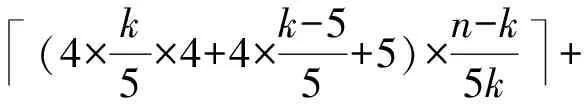
(4×k5×4+4×k-55+5)×n-k5k+
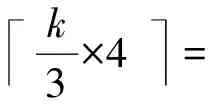
k3×4=
情况2k≡1(mod 5).定义彼得森图上的函数g:
情况2.1当n≡0(mod (3k+1))时,按照如下方式构造意大利控制函数f:
f(vi)=g(vi mod (6k+2))
则f的权重为
情况2.2当n≢0(mod (3k+1))时,按照如下方式构造意大利控制函数f:
其中,h(vi)按照情况1.2中式(1)定义,则f的权重为
w(f)=
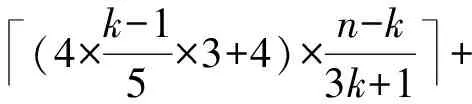
(4×k-15×3+4)×n-k3k+1+
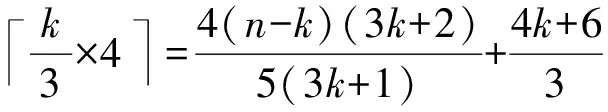
k3×4=4(n-k)(3k+2)5(3k+1)+4k+63
情况3k≡2,3(mod 5).定义函数g如下:

情况3.1当n≡0(mod 5)时,构造意大利控制函数f(vi)=g(vi mod 10),则f的权重为
情况3.2当n≢0(mod 5)时,构造意大利控制函数f如下:
h(vi)按照情况1.2中式(1)定义,则f的权重为
w(f)=

4×n-k5+k3×4=
情况4k≡4(mod 5).定义函数g如下:
情况4.1当n≡0(mod 5k)时,令f(vi)=g(vi mod 10k),则f的权重为
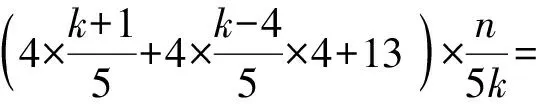
情况4.2当n≢0(mod 5k)时,令
其中,h(vi)按照情况1.2中式(1)定义,则f的权重为
w(f)=

(4×k+15+4×k-45×4+13)×n-k5k+
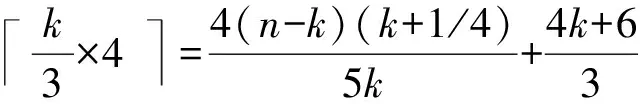
k3×4=4(n-k)(k+1/4)5k+4k+63
由推论1和定理2可以得到下面的定理.
定理3当k≥4时,彼得森图G=P(n,k)的意大利控制数或意大利控制数的界如下:
3 结 语
本文研究了广义彼得森图P(n,k)(k≥4)的意大利控制数.根据图形特点构造了可递推的意大利控制函数,利用函数计算得到了意大利控制数的上界.结合前人给出的意大利控制数的下界,确定了当k≡2,3(mod 5)且n≡0(mod 5)时,P(n,k)(k≥4)的意大利控制数的精确值.对于其他情形下的彼得森图,本文给出了意大利控制数的界.
