以“变”促“思”

摘 要：新课程改革到来，要求初中数学教学不仅要注重基本知识概念的传授，还要培养学生良好的数学思维能力和学习能力.而“变式教学”是拓宽学生思维的重要途径之一，也是初中数学中较为经典的一种教学方法.本文将从数学例题出发，采取“数字”、“条件”、“结论”、“图片”等变式策略，来促使学生感知数学本质，拓宽数学思维，全面提升数学综合能力.

关键词：初中数学;变式教学;数学思维

中图分类号：G632      文献标识码：A      文章编号：1008-0333（2021）32-0002-02

收稿日期：2021-08-15

作者简介：黄李华（1977.10-），男，江苏省启东人，本科，中学一级教师，从事初中数学教学研究.

随着新课改的不断深入，优化课堂形式、创新教学模式成为了当前初中数学教学的主要任务之一.从近年的中考试题来看，我们也不难发现开放性、探究性的题目开始逐渐增多，这就要求考生不仅要掌握基本的数学知识和技能，还要具备良好的数学思维能力.而变式教学是训练思维能力的重要方法之一，它是对现有问题进行深入探究和再次开发的一种高效教学方法，以当前教学理论为基础，设计多变化的问题，从而帮助学生进行知识的建构和思维的拓宽.

一、基于数字变式，扩大问题价值

在初中数学变式教学中，通过改变题目中的数字来进行变式是一种操作较为简单的策略，但改变数字并不是单纯的改变其大小，而是应当根据题目本身，从改变数字以后，该问题存在的价值出发来考虑是否需要变式，真正发挥问题的价值.达到巩固所学知识，激发学习兴趣，有效提升教学效果的目的，真正为学生将来的数学学习铺垫良好的基础.

例1 有一个等腰三角形，已知其中的两条边长分别为3和6，请问还有一条边的长度为多少？可变式为：有一个等腰三角形，已知其中的两条边长分别为5和6，请问还有一条边的长度为多少？例题中的原题目学生们很容易就能得出唯一的答案，那就是第三条边的长度是6，而变式后的题目就需要学生思考题目中给出的边到底哪条是腰哪条为底，也就是这道题的解法应该有两种情况两种答案，通过这样简单的数字变式，来帮助学生加深对“三角形三边关系”知识点的理解与掌握.虽然更换数字的变式是较为简便的一种方式，但教师若能充分发挥变式之后的题目价值，也不失为一种促进学生思维、完善知识建构的好方法.

二、基于条件变式，掌握问题形式

对题目中的相关条件进行变式，以组成一系列题组的策略叫做“条件变式”.这是初中数学变式教学中最主要的形式之一.这种方法可帮助学生掌握问题的多种形式，有效加强对某类题型的理解，从多元化的形式变化中真正探得题目的本质内涵，从而更好的激活学生的探究欲和求知欲，提升的他们数学解题以及应用能力.

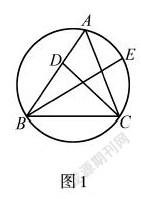
例2 在图1中，△ABC的一条高是CD，BE是图中三角形外接圆的直径，求证：AC·BC= BE·CD;变式1：△ ABC中，∠C 的一条平分线和底边 AB 相交于点D，与三角形外接圆相交于点E，求证：AC·BC= BE·CD;变式2：△ ABC中，边AB的中线与三角形外接圆相交于点F，求证：BC·BF=AC·AF;变式3：△ ABC 中，D是边AB上的一点，E 则为三角形外接圆上的一点，已知∠EBC =∠ACD，求证：AC·BC= BE·CD.原题是一道非常经典的关于三角形知识的例题，学生只需采用“三角形相似性质”的内容就能解答.由于题目中已知的条件是高CD，因此，进行条件变式时可将题目中的“高”变为三角形的一条“角平分线”或“中线”，就能得到变式1和变式2的问题.而学生在一环接一环的变式中，不知不觉就完成了对“高线、角平分线以及中线关系”的探究，促进了学生对三角形知识的灵活运用.同时，还可以进一步加大难度，将特殊条件变为一般条件，即：将高CD转化为一般线段得到变式3的问题，让学生在逐步探究与发现中更加深入的掌握三角形证明题的解法，理解该类题型的内涵，获得数学创新及解题能力的提升.

三、基于图形变式，巩固问题基础

“图形变式”是许多几何题目中常用的一种方法，它是根据某一个基本图形来进行变换延伸，从而得到一系列相关图形的变式设计方法.通过对图形的变式，可以使学生对相关概念掌握得更加透彻，获得巩固基本知识，提升解题能力的效果.当然，要解决这类变式题，关键的点就是要找到图形不变的特征，并分解出其中蕴含的某类基本图形.

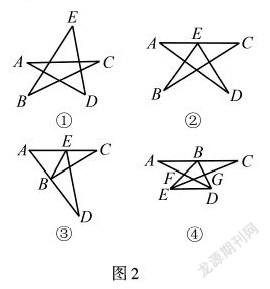
例3 图2①中，五角星的五个内角和即：∠A+∠B+∠C+∠D+∠E等于多少？变式1：图2②中，若将点E向下移到线段AC上，则∠DEB+∠A+∠C+∠D+∠B的和有没有变化？变式2：图2③中，若将点B向上移到线段AD上，则∠CBE+∠BED+∠A+∠C+∠D的和有没有变化？变式3：图2④中，DF与EG分别是线段BE、BD上的中线，若将DF延长至A点，使AF=DF，将EG延长至C点，使CG=EG，那么，AB是否等于BC？点A、B、C是否在一条直线上？并说明理由.原例题学生只需要根据“三角形内角和及外角和”定理，分解出基本图形为三角形，即五个角都在三角形中，就能轻松得出五角和等于180°;变式1与变式2则需要学生根据例题观察图形变化，并进行灵活思考和应用，图形变化但内角和没有改变，因此可得出答案还是180°，让学生进一步感受到图形的多变性和原理的不变性;变式3则更加大了一点难度，对图形进行了更加深入的拓展变式，可有助于激发学生的创新思维，加强学生对相关知识掌握的深度与广度.

四、基于结论变式，深化问题探究

“结论变式”即是改变例题最后所求问题，以达到丰富、拓展相关知识点的一种方式.这类变式设计可有效引导学生从多维角度去思考、发现、分析及拓广相同条件下的结论问题，掌握相关知识内涵，从而获得数学思维能力与探究精神的有效发展.

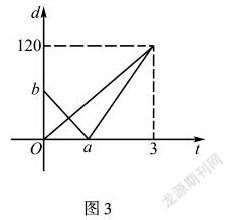
例4 小王和小李在同一时间分别驾车从甲、乙两地出发，两人都是沿着直线匀速行驶，当都行驶到丙地时，乙地正好在甲和丙这条直线上，假设当行驶t小时后，小王和小李两人距离乙地分別有d1与d2千米，而图3则是d1，d2与t的函数关系，请根据图3解答以下问题：1.若甲、乙两地相距20km，则小王的行驶速度为多少km/h？2.请列出d1与t的函数关系式.以上例题可变式为：结论1：当两人相距15千米时他们行驶了多久？结论2：当0     总之，在初中数学教学中，变式教学是非常重要的一种教学方法，它不仅能有效培养学生良好的数学思维，还能通过具有针对性、层次性、探究性的题目变式，使学生掌握问题的本质规律，会一题就会一类题.但值得注意的是，变式教学不应是为了变式而变式，而应当从学生的认知特点出发，掌握一定的度，设计巧妙而适当的变式问题，才能让学生思维得到有效拓宽，提升教学效率，让数学课堂活力无限.

参考文献：

[1]林远达.启迪思维，暴露过程，主体参与，探索创新——谈初中数学变式教学的设计[J].福建中学数学，2007（10）：14-16.

[2]黄亚奇.以“变”促教，引领高效教学——例析初中数学变式训练的实施策略[J].数学教学通讯，2019（05）：68-69+85.

[责任编辑：李 璟]