开阔数学视野,发展理性精神
2021-11-27罗钢
罗钢

摘要:《从百分数想开去》一课,在学生已经掌握百分数相关知识的基础上,尝试挖掘更多的百分数现实应用的素材,从而引导学生用数学的眼光观察世界,开阔数学视野,用数学的思维思考世界,发展理性精神。在教学中,引导学生理解恩格尔系数,判断“是作家,还是司机”,理解“37%规则”,发现“辛普森悖论”,从而感受实证精神以及数据价值,发展数据分析观念,感悟算法思维以及算法价值,提升怀疑精神和严谨作风。
关键词:百分数的应用;理性精神;数据分析观念;算法思维;怀疑精神
“百分数”是小学数学的重要内容,主要包含百分数的意义和百分数的应用等内容。近期,义务教育数学课程标准修订组组长史宁中教授在公开讲座中明确指出,即将颁布的新版课标对百分数内容做了非常大的调整:将其从“数与代数”领域调整到了“统计与概率”领域。在此背景下,笔者尝试深入解读百分数内容并思考如何展开相应的教学。
最近,笔者开设了一节公开课《从百分数想开去》,在学生已经掌握百分数相关知识的基础上,尝试挖掘更多的百分数现实应用的素材,从而引导学生用数学的眼光观察世界,开阔数学视野,用数学的思维思考世界,发展理性精神。
一、理解恩格尔系数,感受实证精神以及数据价值
经济和社会领域,有很多重要的统计数据以百分数的形式出现。这些数据的获得是大量调查的结果,体现了实证精神。通过这些数据,很容易了解一个国家或地区经济或社会某个方面的情况,为政府或公司的政治或商业决策提供重要的参考。在众多经济和社会领域的百分数形式的统计数据中,笔者选择了“恩格尔系数”作为教学素材,因为其实际意义贴近学生的生活经验,其推理结论同样基于生活经验,并具具有一定的思维含量。在教学中,笔者让学生在理解恩格尔系数意义的基础上,思考具体数据的获得及其作用,从而感受实证精神以及数据价值。教学片段如下:
师(PPT出示:2019年我国居民家庭的恩格尔系数是28.2%)这个百分数表示什么意义呢?
(学生摇头。)
师你知道什么是恩格尔系数吗?
生不知道。
师怎么办?
生查资料、百度……
师老师查到恩格尔系数的含义:恩格尔系数表示食品支出总额占消费支出总额的百分比。那么,这里的28.2%表示什么?
生表示2019年我国居民家庭食品支出总额占消费支出总额的28.2%。
师你知道这个数据是怎么来的吗?
生用食品支出总额除以消费支出总额算出来的。
师那么,食品支出总额和消费支出总额又是怎么得到的呢?
生调查统计得到的。
师很好!为什么要调查统计?能不能大概估计一下或者干脆编一个?
生不能!那样就不准确、不真实了!
师很好!具有现实意义的数据一定要准确、真实,否则就没有用了。为了得到我国城镇和农村居民家庭的恩格尔系数,统计部门的工作人员有大量的工作要做。(稍停)那么,得到这个恩格尔系数到底有什么用呢?
(学生面露难色。)
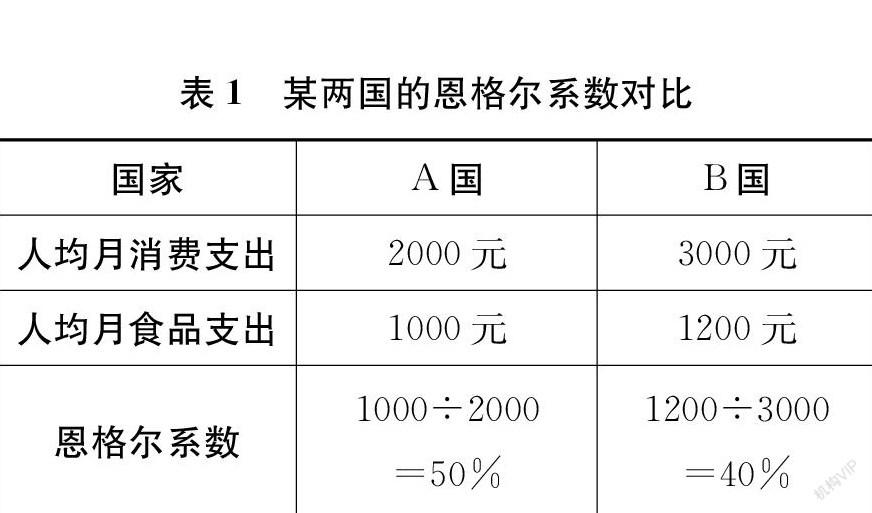
师这个问题确实有点儿难,让我们来举一个例子。(PPT呈现表1,“恩格尔系数”一栏由学生口算答出)现在你有什么发现?
生B国家的人民更富裕,恩格尔系数更低。
生食品支出占比越低,其他支出占比就越高,说明生活就越富裕。
师很好!你能进一步说明为什么恩格尔系数越低,生活就越富裕吗?
生我觉得是因为,不论你有多少钱,总是要吃东西的,而吃东西花的钱都差不多;如果你很有钱,那么吃了东西后还有很多钱可以花在其他地方;如果你的钱不多,那么吃了东西后就没什么钱可以花在其他地方了。
师同学们听明白他的意思了吗?
生明白了。
师是啊!当你很有钱的时候,你才能花较多的钱在吃以外的方面;当你没什么钱的时候,你只能把钱主要用在吃上。所以,恩格尔系数越低,说明生活就越富裕。所以,恩格尔系数是一个国家重要的经济数据,能反映国民的富裕程度。(稍停)那么,2019年我国居民家庭的恩格尔系数是28.2%,它是高还是低呢?
生那需要知道其他年份或其他国家的恩格尔系数是多少,然后进行比较。
师很好!这个事情就留给同学们课后完成:查找其他年份和其他国家的恩格尔系数,看看现在我国人民的生活是贫穷还是富裕。
二、判断“是作家,还是司机”,发展数据分析观念
数据分析观念(或者说统计思维、数据思维)既包括采集多维数据反映事物属性,也包括灵活分析数据作出结论判断,即利用数据解决问题。现实中,可以利用数据解决的问题非常多。笔者选择了一个判断“是作家,还是司机”的问题作为教学素材。对这个问题,基于直觉(感性)很容易作出错误判断,而依托数据分析(理性)才能作出正确判断,因而,可以很好地培养学生的数据分析观念,同时渗透“敢于不精确,不能太离谱”的估算意识和方法。教学片段如下:
师有这么一个人,他善于观察,又多愁善感,在大街上看到一片落叶,就感叹时光飞逝、青春不再;他热爱生活,又内向沉默,只有特别熟了之后,才能真正跟他聊起来。问题来了:你觉得他更有可能是一位作家,还是一位司机?认为他更有可能是作家的请举手。
(超过一半的学生举手。)
师你们为什么认为他更有可能是作家?
生因为作家中多愁善感的比较多。
师你認为作家中多愁善感的约占多少?司机呢?
生不知道。
师大胆估计一下,不太离谱就行。
生作家中约占80%,司机中约占30%。
师好的。仅凭这两个数据,就能得出“他更有可能是作家”这个结论吗?有不同的想法吗?
生这两个百分数的单位“1”不同,所以无法比较。
师那你觉得还需要哪些数据?
生作家的人数和司机的人数。
师作家的人数和司机的人数我们都不知道,怎么办?
生可以去调查一下。
师是的,调查是获得准确数据的重要方法,但是操作起来比较麻烦。对“判断他更有可能是作家,还是司机”这个问题,我们不需要那么精确的数据,而可以像刚才那样大胆地做一个不太离谱的估计。假设作家人数是1份,根据我们的生活经验,司机人数用几份来表示比较合理?
生滿大街都是司机,司机人数要远远超过作家人数,估计司机人数是100份。
师好的。假设某城市的作家人数是100人,那么司机人数是10000人。由此,我们就可以计算了。请你来计算一下多愁善感、沉默内向的作家和司机各有多少人。
(教师根据学生的计算结果板书,内容如图1。)
师看来,真实的情况是:他更有可能是司机。用数据来说话,这就是数据分析观念,或者说数据思维。运用数据思维可以让我们跳出直觉误区,作出更加理性的判断。当然,要想得到更加严谨的判断,我们还需要更加准确的数据。
三、理解“37%规则”,感悟算法思维以及算法价值
大量的统计数据中蕴含着规律。百分数除了作为统计数据出现,还可能作为规律要素出现。这时,蕴含百分数的规律往往能体现出算法思维。算法思维的一种比较肤浅的理解是以(广义的)计算的方式解决问题,而本质上则是计算机思维(或者说人工智能思维)。作为一种理性思维,它的基本特点是程序化、可操作性,最终指向是能够利用计算机(人工智能)完成。通过解方程解决算术问题、通过解析几何方法解决平面几何问题便是算法思维的体现。小学生真正理解算法思维是比较困难的,笔者选择了比较好懂又很有用的“37%规则”作为教学素材,让学生体会到生活中的很多问题都可以通过算法帮助解决,初步感悟算法思维以及算法价值。教学片段如下:
师生活中,我们经常会遇到这样的问题,那就是做一些重要的决策。如买房时,什么情况下最该出手?一看见好的就出手是比较草率的,但是迟迟不做决定也会错失良机。怎么办?
(学生面露难色。)
师别急,数学家已经帮我们解决了这个问题。《指导生活的算法——人类决策中的计算机科学》一书告诉我们,数学家经过一系列复杂算法,把决策问题变成了随机选择优化问题,并利用“37%规则”解决了它。以买房为例,“37%规则”把决策过程分为两个阶段,第一个阶段只看不买,同时记住最好的; 第二个阶段遇到更好的或类似的,就毫不犹豫地买下来。“37%规则”不能保证你买到最好的,但能让你在足够少的时间内买到足够好的房子。你是如何理解“37%规则”的?
生37%是指考虑的时间占总时间的37%。
师如果总时间是100天,怎么解释37%?
生也就是,前37天考察比较,从第38天起看到更好的或类似的,就毫不犹豫地买下来。
师课前,同学们都思考或调查了自己或家人、朋友近期需要作出的比较重要的决策以及完成这个决策最长的期限。现在,让我们一起来运用“37%规则”给自己或家人、朋友做一个最优化的决策:计算从大约从什么时候开始作出决策。
(学生计算,然后教师组织汇报、交流。)
师看来,我们在学习、工作、生活中,不是只能凭感觉作出一些决策,还能运用算法思维作出更好的决策。
四、发现“辛普森悖论”,提升怀疑精神和严谨作风
百分数是一个“率”,如果忽视其中相比的两个更基本的“量”的大小,而只考虑这个算出来的“率”的大小,则很容易导致错误的判断。学生认识到直觉不可靠,而数据分析更可靠后,笔者选择了“辛普森悖论”作为教学素材,让学生经历“数据分析—得出结论—提出质疑—再次分析—推翻结论”的过程,感受到数据的“欺骗性”,从而培养怀疑精神和严谨作风,进一步提升理性精神。教学片段如下:
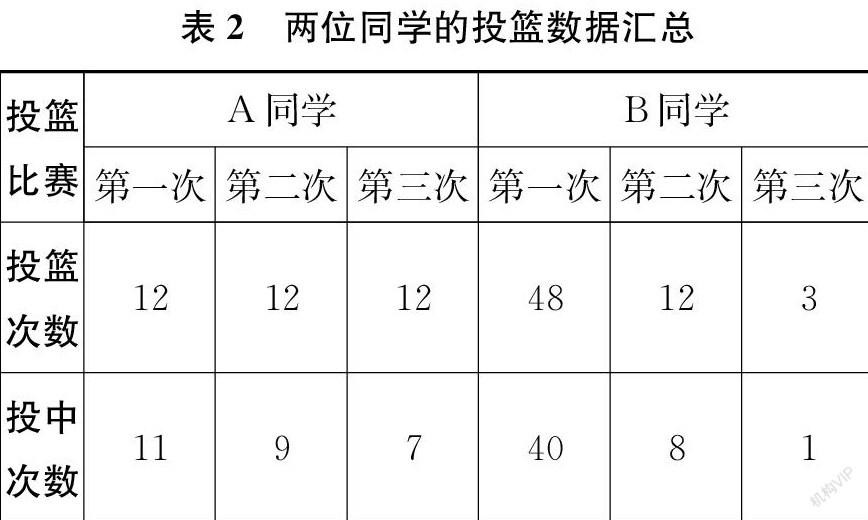
师A同学和B同学进行了三次投篮比赛,谁的成绩更好呢?还缺什么?
生数据。
师(PPT呈现表2)有了这些数据,你们认为谁的成绩更好?你是怎么想的?
生我认为A同学的成绩更好。我算过了,A同学三次比赛的命中率分别为91.7%、75%、58.3%,B同学三次比赛的命中率分别为83.3%、66.7%、33.3%。三次比赛,A同学的命中率都比B同学高。
师三场比赛,A同学的命中率都比B同学高,就可以得出A同学的总体成绩比B同学好吗?你们确定吗?还有没有别的算法?
(学生开始重新思考并计算。)
生我换了一种方法计算,A同学三次比赛的总命中率为(11+9+7)÷(12+12+12)=75%,B同学三次比赛的总命中率为(40+8+1)÷(48+12+3)≈77.8%。虽然单次的命中率都是A同学更高,但总命中率却是B同学更高。
师是啊!这说明B同学的投篮成绩更胜一筹。这个现象是由英国统计学家爱德华·辛普森首次发现的,所以叫作“辛普森悖论”。这个悖论说明百分数有一定的“欺骗性”,会干扰我们的判断。同学们想破解谜题,摸清“辛普森悖论”背后的原因吗?看来今天数学课后,同学们有了一个新的研究方向。
参考文献:
[1] 吴军.数学之美(第二版)[M].北京:人民邮电出版社,2014.
[2] 乔占周.高等数学教学中渗透数学文化的思考[J].教育现代化,2017(10).专题研究
