水面船形状因子的CFD计算研究
2021-11-26吴乘胜王建春金奕星
王 星,吴乘胜,赵 峰,王建春,金奕星
(中国船舶科学研究中心,江苏无锡 214082)
0 引 言
阻力性能是船舶最重要的水动力性能之一,阻力预报则是船舶设计过程中进行航速预报时必不可少的工作。基于模型尺度的水池试验或模型试验结果预报实船阻力,是目前主要的技术手段,而将模型尺度的船模阻力换算成实船阻力的具体方法有多种,目前常用的主要包括二因次法和三因次法[1]。
最早的体系性的实船阻力换算方法是傅汝德提出的二因次法,该方法将船体总阻力分成摩擦阻力和剩余阻力,并认为摩擦阻力仅与雷诺数(Re)有关,剩余阻力仅与傅汝德数(Fr)有关,且二者互不干扰。
由于二因次法无法考虑船体的三维形状与平板的差异所产生的对粘性阻力的影响,在其基础上,休斯提出将船体阻力分成与Re相关的粘性阻力和与Fr相关的兴波阻力,并且认为粘性阻力中的粘压阻力系数与摩擦阻力系数的比值是常数k,1+k就是形状因子,与船体形状有关。这种实船阻力换算方法中引入了形状因子,即为三因次法。由于三因次法考虑了船体三维形状的影响,理论上更为合理,目前广泛应用于各大水池的船模阻力试验预报中。
使用三因次法换算实船阻力,关键问题是如何确定形状因子1+k。传统的形状因子确定方法主要基于船模低速拖曳试验,采用Prohaska 方法或ITTC’1978 方法获得[1](这两种方法分别将兴波阻力系数表示为正比于Fr的4次和n次方的形式)。然而,通过水池模型试验获得形状因子并非易事,因为低速拖曳状态下,船模阻力较小,易受各种因素的干扰,导致测量结果相对误差较大,在给模型试验带来一定难度的同时,也会影响形状因子计算的准确度。
近年来,CFD应用技术正高密度融入预报-评估-设计,为船舶水动力学性能研究和船型设计的创新发展提供了前所未有的利器。而在形状因子的计算和研究中,CFD技术有着其独特的优点:一是可以采用叠模计算,可以完全排除兴波的影响;二是可以在较大的航速范围内开展计算,研究Re数等对形状因子的影响(模型试验由于必须在低速工况下开展,因而难以实现)。
国内外不少研究人员都利用CFD 技术开展了形状因子研究。Kouh 等[2]应用CFD 技术,针对Wig⁃ley船、KVLCC2、DTMB5415、DTRC4621、一艘渔船和一条鱼雷,开展了船舶形状因子的尺度效应研究,结果表明形状因子随Re大致呈线性增大的趋势;Shen 等[3]针对细长型回转体(长径比11~13),运用数值方法,研究并推导了由模型剩余阻力换算实船/艇阻力的外推公式,并提出模型尺度下的形状因子数值与实船尺度下的呈现明显差异;王金宝等[4]研究了肥大型船舶形状因子的CFD 计算方法,通过对多艘肥大型船舶形状因子的CFD 计算并与模型试验结果的比较,以及典型船舶航速预报与实船测试结果的比较,表明采用CFD 计算获得的形状因子(1+k)可以用于肥大型船舶实船阻力的三因次换算;江杰等[5]则应用CFD 技术,针对DTMB5145和KCS,研究了航行姿态及尺度效应对形状因子的影响,结果表明二者均会导致形状因子增大。
当前,CFD与EFD结合用于船舶航行性能研究和预报,已成为趋势和共识的技术手段。通过CFD计算水面船形状因子并用于实船阻力预报,便是一种典型的应用。由于形状因子中的k是个小量(通常在0.1~0.2左右),对CFD求解器和计算方法的精度、可靠性和分辨力等都有很高的要求。
本文介绍了针对水面船形状因子所开展的CFD计算研究。由于计算域中船舶艏部和艉部附近不可避免地会存在低正交性、高扭曲率的低质量网格,对计算结果影响很大,如处理不当,会对计算精度和稳定性产生不利影响。为解决这一问题,在CFD 求解器中引入了非正交修正和梯度限制器。本文针对KVLCC2、KCS 和“育鹏”轮三种典型船型,开展了水面船形状因子CFD 计算研究,并对计算结果进行了不确定度分析。结果表明,形状因子CFD 计算结果以较高水平通过了不确定度分析的验证和确认,说明CFD求解器较好地解决了关键局部区域低质量网格带来的问题,能够以较高的精度计算水面船形状因子。
1 数值计算方法
1.1 CFD求解器简介
船舶水动力学CFD 求解器NaViiX(Naval Hydrodynamics Oriented CFD Solvers),由中国船舶科学研究中心独立自主研发,具有完全自主知识产权,目前具备以下功能:(1)能够实现三维航行体单相、两相(带自由面)湍流绕流CFD 模拟;(2)支持结构化网格、非结构化网格、混合网格、交界面网格和滑移网格;(3)支持标准k-ε、RNGk-ε、k-ω和SSTk-ω湍流模型;(4)支持惯性坐标系、非惯性坐标系和多参考坐标系求解;(5)支持MPI并行计算。
通过大量的CFD 计算研究[6]并结合以前的实践经验[7],本文的数值计算与分析,采用基于RANS方程(Reynolds Averaged Navier-Stokes Equations)的CFD方法,其中湍流模型使用RNGk-ε模型。控制方程具体形式详见文献[6-7]。
CFD 求解器采用有限体积法(Finite Volume Method,FVM)离散控制方程,其中对流项采用二阶迎风差分格式,扩散项采用中心差分格式,压力速度耦合采用SIMPLE(Semi-Implicit Method for Pressure Linked Equations)算法解耦,代数方程组使用Gauss-Seidel 迭代求解,并使用代数多重网格(Multigrid)技术加速收敛。
前面提到,由于船舶形状因子中的k是个小量(通常在0.1~0.2左右),对CFD求解器和计算方法的精度、可靠性和分辨力等要求很高,因而常常需要使用正交性高、扭曲率低的高质量结构化网格。但水面船几何外形是复杂的三维曲面,在生成结构化网格的过程中,难免会存在高扭曲率、低正交性的低质量网格,这些网格通常出现在船舶艏部和艉部附近。而船舶艏部和艉部通常曲率变化大,空间流动复杂,速度、压力等物理量时空变化剧烈,且对计算结果影响巨大甚至是决定性的,如果处理不当,不但会影响计算精度,还会影响计算稳定性,甚至会造成计算发散。
为解决上述问题,在CFD求解器中引入了非正交修正和梯度限制器,以下分别进行简要介绍。
(1)非正交修正
非正交修正具体是针对控制方程扩散项的离散。输运方程中,扩散项表达式如下:

式中,γ是控制体单元界面的扩散率,S则为界面的面外法向矢量。扩散项离散后可分为正交部分和非正交部分[8],见式(2)。对于网格正交性较好的部分,第二部分可直接忽略,但当网格单元正交性低、扭曲率高时,加入非正交部分可有效保证计算精度和稳定性。
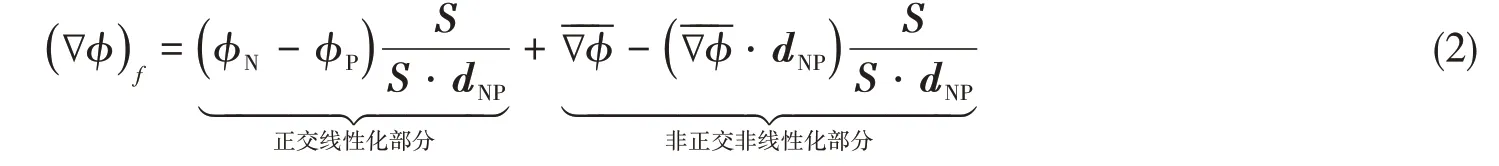
式中,连接向量dNP=xN-xP,xP为控制体单元中心坐标,xN则是控制体单元界面f所对应的相邻单元中心坐标可利用控制体单元与相邻单元的变量梯度值通过线性插值得到。
(2)梯度限制器
在同位网格中,流场变量值存储在控制体单元中心,而单元界面的变量值φf,P则需要通过控制体单元φP重构获得,表达式为

式中,连接向量d=xf-xP,xP和xf分别是控制体单元中心和界面中心坐标,( )∇φP为单元中心处变量梯度。
在重构过程中,为了避免出现新的极大值和极小值,需要引入梯度限制器。常见的梯度限制器有Barth and Jespersen限制器和Venkatakrishnan限制器[9]。本求解器使用改进的Venkatakrishnan限制器,该限制器在精细流动以及非定常流动模拟中具有更小的数值耗散。具体表达式为
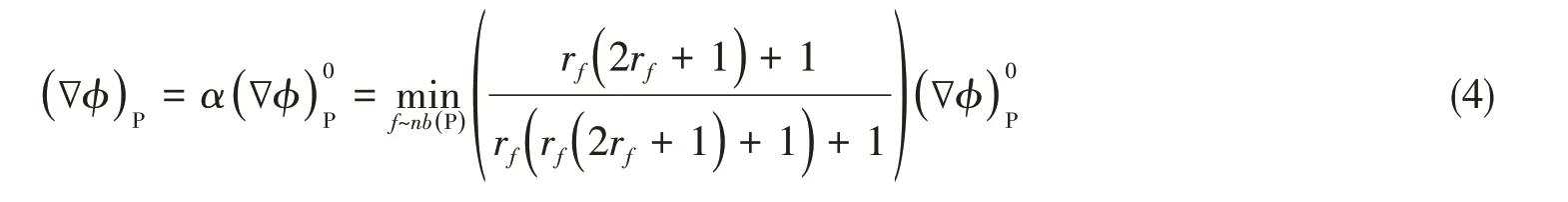
式中,
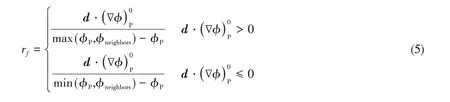
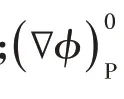
图1 给出了针对一典型算例——CFD 求解器使用非正交修正和梯度限制器前后阻力收敛历程的对比。从图中可以看出:在使用前(左图),整个计算过程中压差阻力收敛历程呈不规则振荡,且振荡幅度很大,摩擦阻力收敛历程也存在一定振荡,不过幅度较小而已;在使用后(右图),压差阻力和摩擦阻力都是在经历计算初始阶段的振荡后,很快趋于平稳收敛的状态。
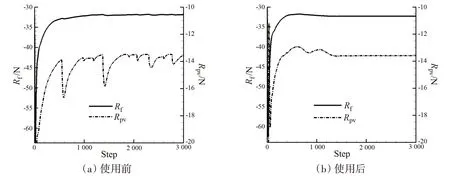
图1 阻力收敛历程比较Fig.1 Comparison of convergence histories of resistance
可见,CFD求解器在引入非正交修正和梯度限制器之后,计算更加稳定,同时收敛速度也有所提高。
1.2 计算区域、网格划分与边界条件
为排除兴波的干扰,CFD计算采用重叠模,即静水面作为对称面处理;同时由于船舶左右对称,且流动是定常或准定常的,同样具有对称性,CFD 模拟时只需计算一半区域(如图2 所示)。计算区域范围参考了相关文献[7]的研究成果,其边界如下:(a)前端——模型首部前约1.2 倍船长处,设置为入口边界条件;(b)后端——模型尾部后约2.4 倍船长处,设置为出口边界条件;(c)外边界——模型外侧约1.2 倍船长处,设置为入口边界条件;(d)对称面——模型中纵剖面的延展面和静水面,设置为对称面边界条件;(e)船舶模型表面——设置为无滑移壁面边界条件。
计算网格为多块分区的H-O 型结构化网格(纵向H 型、横向O 型,如图2 所示),网格划分的基本原则为:船模艏部和艉部等曲率变化较大部分网格加密、舯部网格相对较为稀疏;模型近壁面附近网格加密,其中近壁面第一层网格法向高度根据y+确定(y+平均约为45)。
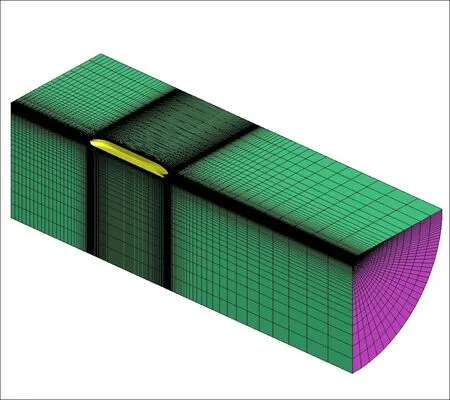
图2 计算区域及网格示意图Fig.2 Computation domain and meshes
CFD 计算中,边界条件的具体设置如下:(a)在入口边界上,根据船模前进速度,给定入口流动速度;(b)出口边界距离船模足够远,其压力分布设置为静水压力;(c)在船模表面,引入标准壁面函数;(d)在对称面上,满足对称条件。
2 研究对象与计算工况
2.1 研究对象
CFD计算研究针对三型船模开展,分别为KVLCC2、KCS和“育鹏”轮。这三型船模很具有典型性:KVLCC2 是由韩国船舶与海洋工程研究所(Korean Research Institute for Ship and Ocean Engineering,KRISO)设计的30 万吨VLCC 船型(实船并未建造),共有两种线型,目前国际通常采用的是第二种线型,即KVLCC2,是典型的低速大方形系数船型;KCS 是一艘带球鼻艏的集装箱船(实船并未建造),也由KRISO 设计,是典型的中高速中等方形系数船型;“育鹏”轮是一艘多用途教学实习船,航速和方形系数介于KVLCC2和KCS之间,也代表了近年来集装箱船低速化的一种趋势。
CFD 计算研究的三型船模主尺度参数见表1,图3 给出了KVLCC2、KCS 和“育鹏”轮船模几何外形。

表1 KVLCC2、KCS和“育鹏”轮主尺度参数Tab.1 Main particulars of KVLCC2,KCS and YUPENG

图3 船模几何外形Fig.3 Geometry of ship models
2.2 计算工况
CFD计算分别针对三型船模设计吃水状态下的两个航速(设计航速和较低航速)开展,计算工况列于表2中。

表2 船模形状因子CFD计算工况Tab.2 Computational cases for form factor of surface ships
对三型船模,都采用三套网格来进行数值预报,网格在轴向、周向和径向三个方向上按 2 的加细比细化:对KVLCC2船模,三套网格的网格数分别为35万、100万和260万;对KCS船模,三套网格的网格数分别为31万、90万和240万;对“育鹏”轮船模,三套网格的网格数分别为33万、91万和240万;网格细化过程中,近船模表面第一层网格法向高度保持不变(y+平均约为45)。
表3给出了三型船模三套网格中高质量网格(扭曲率0.3以下)和低质量网格(扭曲率0.7以上)的比例。网格扭曲率定义如下(以四边形面单元为例):
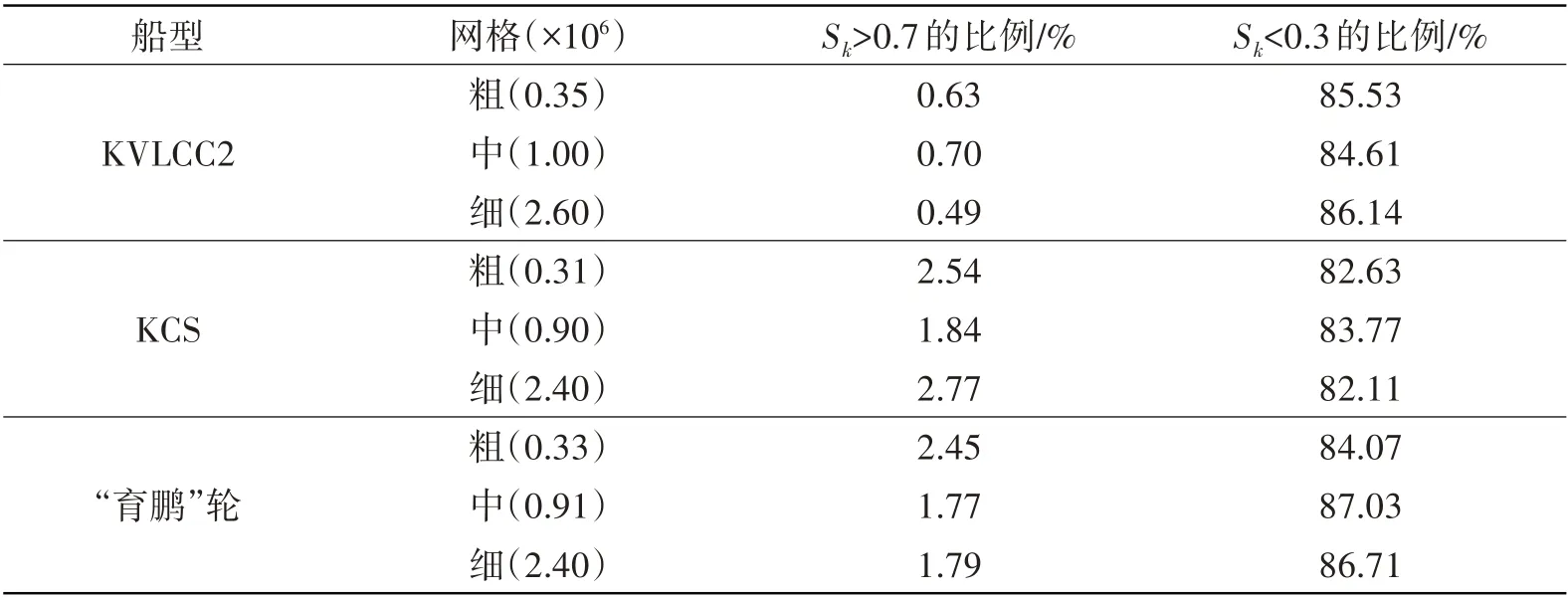
表3 计算域网格单元扭曲率Tab.3 Skewness coefficients of grid cells in computational domain

式中,θ为网格单元的最大或最小内角。
从表3中可以看出:计算域中高质量网格占大多数,比例在85%左右;低质量网格比例很小,占比不超过3%,且大多在2%以下。高扭曲率的低质量网格比例虽然不大,但绝大部分位于船模艏部和艉部附近这些关键区域,如图4 所示(图中红色区域表示网格单元扭曲率高),对数值计算的影响很大,也给船模形状因子的准确、稳定计算带来了很大的挑战。
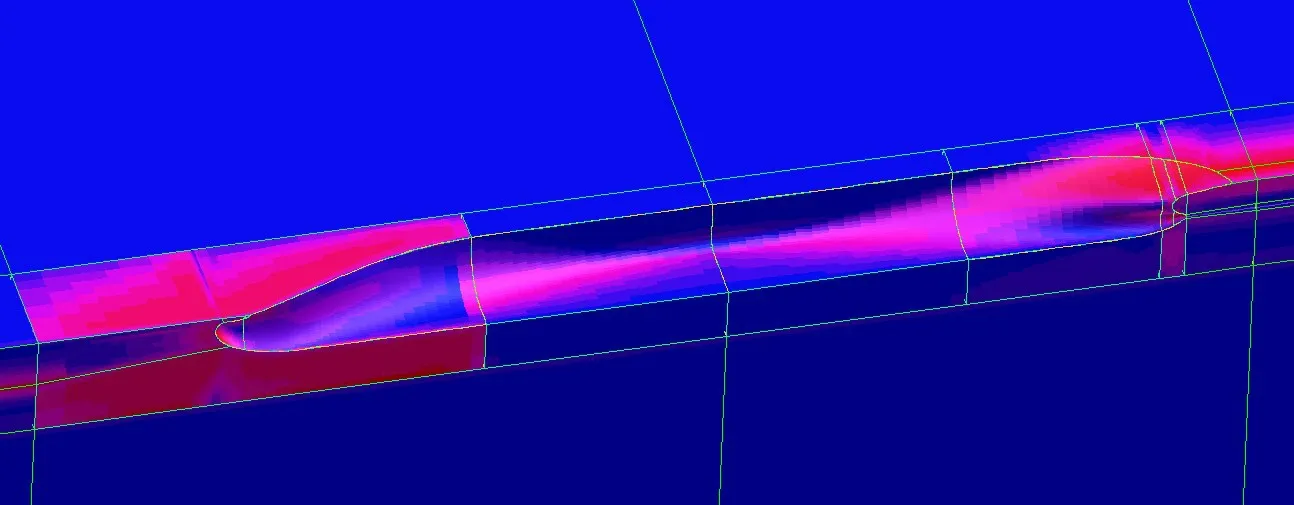
图4 船体附近网格单元扭曲率分布Fig.4 Distribution of skewness coefficients of grid cells in the vicinity of ship hull
3 计算结果与分析
3.1 计算结果
通过叠模CFD计算获取水面船形状因子,其定义为


表4给出了KVLCC2、KCS和“育鹏”轮船模在设计航速和较低航速下的阻力系数和形状因子计算结果,表中同时给出了设计航速下的形状因子模型试验结果[10-11]。图5给出了三条船模在不同航速下形状因子随网格数量的变化曲线,图中同样也给出了设计航速下的形状因子模型试验结果(图中虚线所示)。

表4 船模阻力及形状因子计算结果Tab.4 Computational results of resistance and form factor

图5 船模形状因子计算结果随网格数量变化Fig.5 Computational results of form factor varying with grid cell number
由表4和图5可见,三条船模的总阻力系数和形状因子计算结果随网格数的增加逐渐减小并趋于收敛——细网格和中网格计算结果之间的差异基本都在1%以内,且形状因子CFD计算结果收敛于模型试验结果。
3.2 计算结果不确定度分析
根据ITTC 推荐的CFD 不确定度分析规程[12]及相关指南[13-14],对形状因子计算结果进行不确定度分析,包括验证流程和确认流程。在分析过程中,定义下标“1”代表细网格,下标“2”代表中网格,下标“3”代表粗网格。
(1)验证流程
以KVLCC2设计航速工况为例,相邻两套网格对应的形状因子计算结果之差为
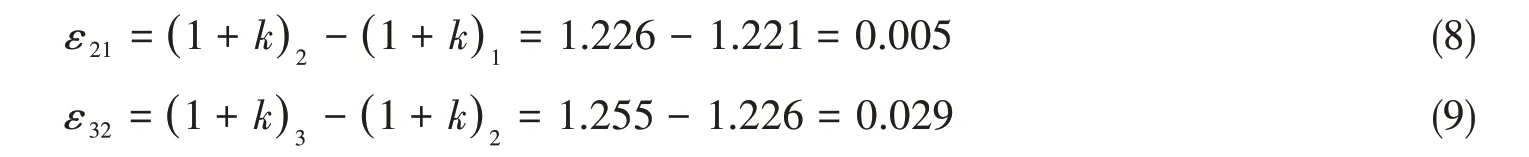
网格收敛因子为

由于0 修正因子CG的计算如下,其中按照文献推荐Pth=2: CG= 4.800显著大于1,则不确定度UG为 类似地,可以进行其他计算工况和其他船模计算结果的验证。KVLCC2、KCS 和“育鹏”轮船模形状因子计算结果的验证列于表5 中。从表中可以看出,三条船模形状因子计算结果的验证水平比较高,最大也不过在1+k的2%左右。 表5 形状因子计算结果的验证Tab.5 Verification of computational results of form factor (2)确认流程 形状因子CFD 计算结果的高水平确认并非易事,原因不在于CFD 计算而在于模型试验。前面说过,通过水池模型试验获得形状因子并不容易,测量结果相对误差较大,也就是试验结果的不确定度较大,一般情况下也很少给出形状因子试验结果的不确定度。 为了进行CFD 计算结果的确认,必须要有模型试验结果的不确定度。为此,这里根据式(1)形状因子的定义,由船模(叠模)总阻力模型试验结果的不确定度,推算形状因子的不确定度。 假设船模(叠模)总阻力系数的不确定度为1%,则根据式(7),形状因子模型试验结果的不确定度为(1+k)%。需要说明的是:对于船模(叠模)阻力模型试验而言,1%的不确定度是正常水平;但形状因子通常是由船模低速拖曳试验确定的,由于此类试验测量结果相对误差较大,总阻力1%的不确定度水平可能难以达到,从而导致形状因子的不确定度较大。因此,对形状因子CFD 计算结果而言,确认的标准偏于严格。 同样以KVLCC2设计航速计算工况为例,比较误差和确认不确定度的计算为 式中,D为模型试验结果,对于本算例,D=1.219。 由于 |E| 类似地,可以进行其他船模计算结果的确认。需要说明的是,由于没有较低航速工况下的形状因子模型试验结果,无法进行对应工况下CFD 计算结果的确认,因此这里仅给出KVLCC2、KCS 和“育鹏”轮船模设计航速工况下计算结果的确认,结果列于表6 中。从表中可以看出,三条船模形状因子CFD计算结果的比较误差均小于确认不确定度,也就是都通过了UV水平的确认。 表6 形状因子计算结果的确认Tab.6 Validation of computational results of form factor 通过对三种典型船型形状因子的CFD 计算研究与分析可知:船模形状因子CFD 计算结果随网格数增加逐渐减小,并收敛于模型试验结果;船模形状因子CFD计算结果以较高水平通过了不确定度分析的验证和确认。 综上,通过本文的研究工作可见,通过引入非正交修正和梯度限制器,自主研发的CFD 求解器较好地解决了船模艏部和艉部附近这些关键区域低质量网格给数值计算带来的问题,能够以较高的精度计算水面船形状因子,可以服务于船舶快速性性能的研究和预报。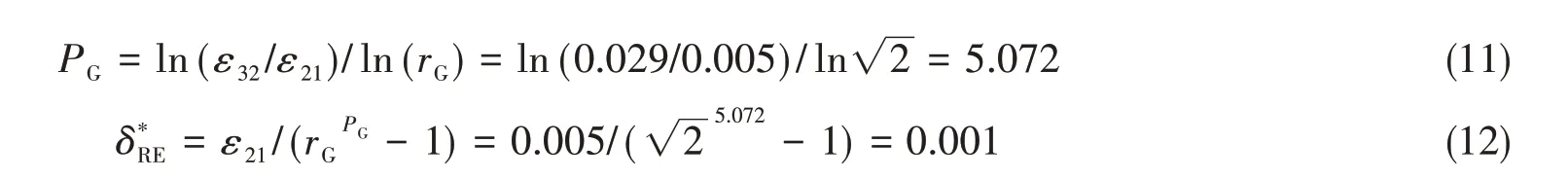





4 结 语
