四桨船伴流场研究

洪智超，宗 智，刘 昆

（1.江苏科技大学，江苏镇江 212100；2.大连理工大学，辽宁大连 116024）

0 引 言

随着人们对船舶航速要求的提高，常规的单桨推进已经很难满足高速船的推进要求了。对于高速船来说，喷水推进是比较理想的推进方式，但因其造价高、结构复杂和维护困难[1]，大多数高速船是使用多桨推进的方式来满足高速船的推进需求[2]。与单桨推进不同，多桨船各桨之间存在负荷差。且负荷差产生的原因较为复杂，因此导致多桨船设计较单桨船更为复杂。单桨推进的研究经过多年的发展已经较为成熟，而与多桨推进相关的研究则开展较少。Labberton[3]就指出四桨船内外桨存在负荷差，并提出一种修改螺距比的方法来平衡内外桨的负荷差。Shrubsole[4]指出当时将中桨与单桨船等同看待的三桨船的设计理论是不正确的，他认为中桨和边桨之间存在的干扰会使中桨和边桨的伴流分数与单桨船有所不同，并在此假设基础上进行试验，使得一条三桨船的燃油费用下降了10%。Abramowicz gerigk[5]通过试验对一条双桨船的尾流场进行了研究，探讨了螺距及转速等对尾流场的影响。Tan[6]通过对一条三桨船进行试验分析提出了一种确定三桨船推进因子的方法。Gao等[7]使用RANS方程结合螺旋桨升力面理论，通过力场模型将船舶和螺旋桨性能预报耦合，模拟了四桨船尾部流场的结构和形态。李景熹等[8]使用CFD 方法对一艘四桨推进的船舶进行数值模拟，分析螺旋桨布局对螺旋桨推力系数、转矩系数以及敞水效率的影响。常欣等[9-10]使用面元法对四桨两舵推进系统的水动力干扰进行了研究。Bi等[11-12]对一艘四桨船进行了试验研究，并提出用干扰因子来指导多桨船的推进器设计。

本文使用CFD方法对一艘四桨船进行研究，计算了敞水桨、船后伴流、船后内桨、船后外桨及船后四桨等工况。结果表明四桨在敞水中运行时，内外桨间干扰较小，可以忽略；内桨在船后运行时负荷较敞水桨增大；外桨在船后运行时负荷较敞水桨略有增加；与船后内桨单独运转相比，船后四桨同时运转时内桨负荷增加；与船后外桨单独运转相比，船后四桨同时运转时外桨负荷减小，但幅度不大。据此本文提出原生伴流和次生伴流的概念：原生伴流为内桨或外桨单独在船后运转时的伴流分数，主要由船体形状决定，次生伴流为内外桨在船后运行时互相干扰而产生的伴流。

1 数值方法

本文采用商业CFD 软件STAR-CCM+对四桨船伴流问题进行研究。基于RANS 方程数值计算的控制方程包括连续性方程、体积分数方程、动量方程和k-ωSST湍流模型。

1.1 控制方程

为了求解不可压粘性流体，求解其中采用的控制方程为

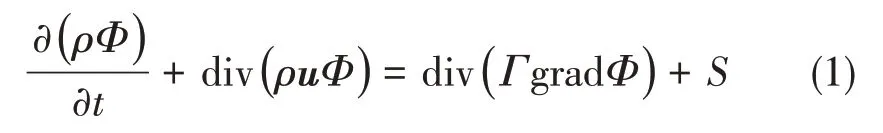
式（1）为控制方程的通用格式。式中：Φ为通用变量，可以代表u、v、ω、T等求解变量；Γ为广义扩散系数；S为广义源项。对于特定的方程，Φ、Γ、S具有特定的形式，各变量与特定方程的对应关系见表1。

表1 通用控制方程中各符号具体形式Tab.1 Concrete form of symbols in general control equation

1.2 自由液面捕捉

本文使用VOF 方法捕捉自由液面。该方法将水和空气看成是同一介质，在整个流场中定义一个流体体积函数Φ，在网格单元中Φ为一种流体的体积与网格体积的比值，如果Φ= 1则单元中充满目标流体，如果Φ= 0 则网格单元中为另一种流体，在Φ从0～1 迅速变化的区域即为自由界面。如果设计算区域为Ω，流体A所在的区域即为Ω1，而流体B所在区域记为Ω2，则首先定义如下函数

对于两种不相容的流体组成的流体，α(x,t)满足

在每个网格Cijk上做积分，并定义VOF函数

于是，函数Φ满足

在数值计算过程中，每个网格对应一个Φ值，只要求出Φ值就可以构造出自由液面形状。

1.3 湍流模型

本文采用k-ωSST湍流模型的输运方程如下：

k的输运方程为

ω的输运方程为

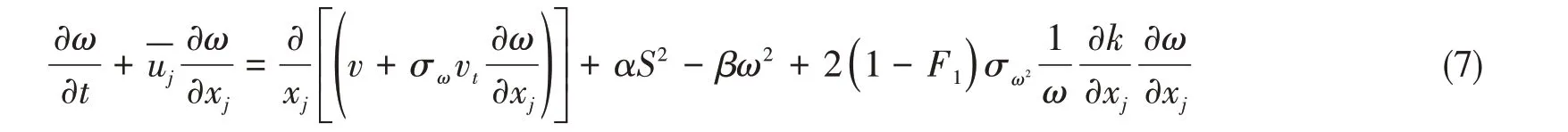
受篇幅限制，此处仅给出基本的方程，详细内容请参考STAR-CCM+帮助文件[13]。

2 数值计算方法验证

为验证数值计算方法的有效性，本文分别对螺旋桨在敞水状态下和自航状态下的数值模拟进行了不确定度分析，不确定度分析所使用的船体模型为大连理工大学的PM06，螺旋桨为B5-105桨。不确定度分析所用船体和螺旋桨的模型参数分别见表2和表3，该模型的试验由Bi等[12]完成。

表2 PM06船模型主要参数Tab.2 Main parameters of PM06 ship model

表3 B5-105螺旋桨模型参数Tab.3 Parameters of B5-105 propeller model

不确定度分析按照Stern等[14-15]提出的方法进行分析。本文分别对螺旋桨敞水和自航的数值模拟进行了验证（verification）和确认（validation），进行验证和确认时，进速系数均为0.799。此外，受测量设备的精度和螺旋桨尺寸较小的影响，KQ的试验数据仅具有指导意义，因此验证和确认都只以KT为指标进行。不确定度分析中所用到的数值计算工况见表4，表中网格1 到3 逐渐变疏，敞水数值计算中网格1、2、3的网格数分别为4.56×106、1.44×106、0.54×106；自航数值模拟中网格1、2、3的网格数分别为8.85×106、3.92×106、2.02×106。

表4 不确定度分析工况表Tab.4 Simulation conditions for uncertainty

2.1 单桨敞水不确定度分析

不确定度分析包括验证（verification）和确认（validation）两部分。单桨敞水数值计算的验证部分通过对单次迭代和网格尺寸进行收敛性分析来实现。单次迭代的不确定度评价对象为KT，图1 是数值计算稳定后KT的一部分时历曲线。在该图中KT的不确定度约为0.14%D，其中D为KT的试验测试结果。迭代的不确定度用迭代过程中峰峰值的一半占试验结果的百分比来表达。使用网格2和网格3进行数值模拟时，迭代不确定度分别为0.15%D和0.26%D。三个网格尺度下迭代不确定度的值都很小，相对于网格不确定度来说可以忽略。

图1 网格1单桨敞水的KT时历曲线Fig.1 Iterative history of KT for single propeller in open water with Grid 1

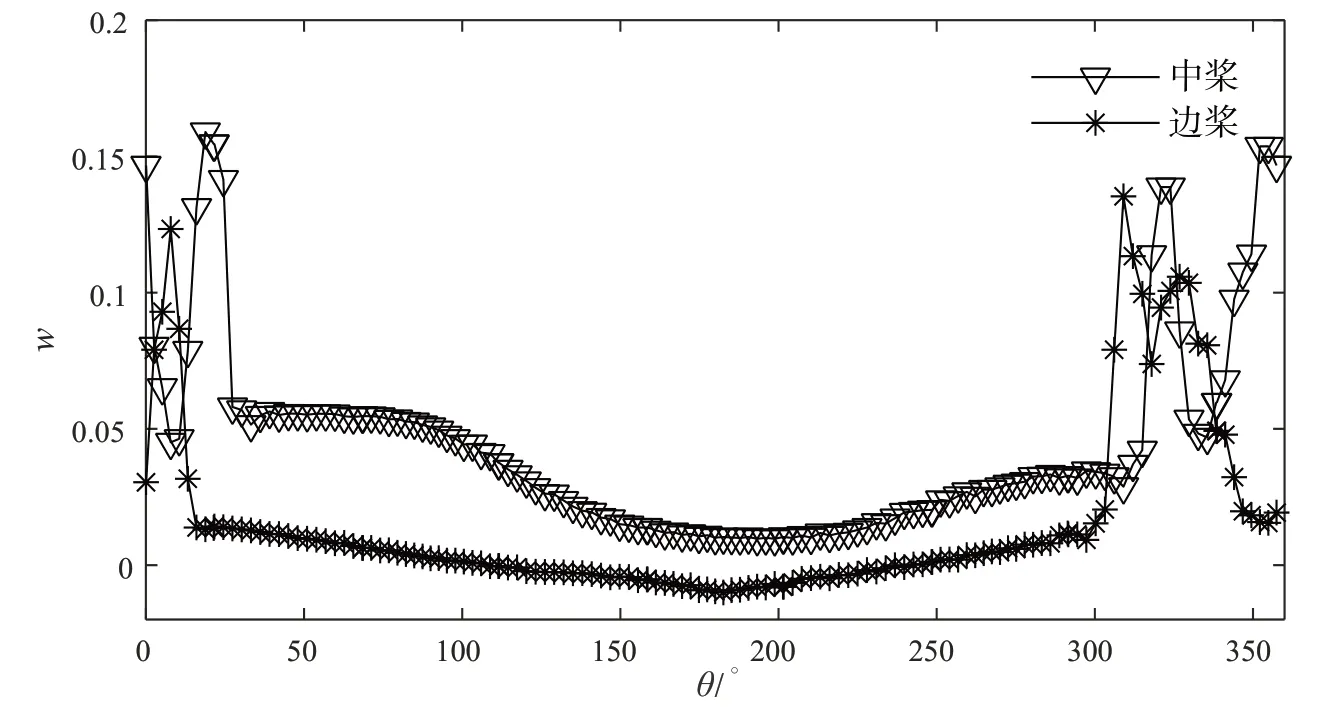
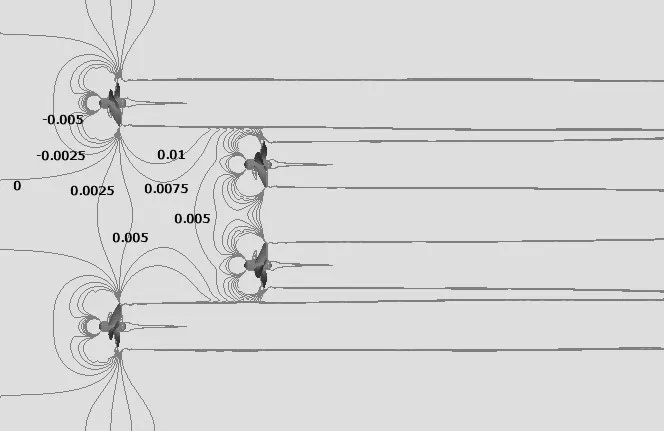
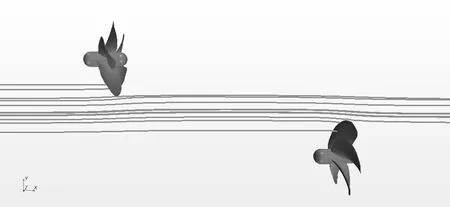
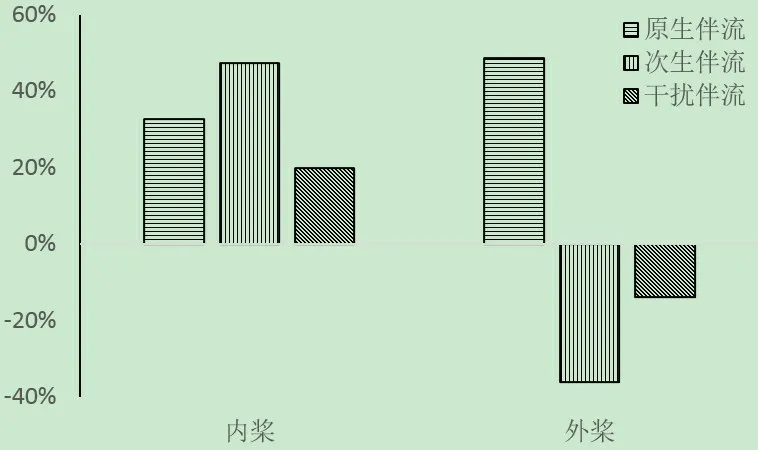
以KT为对象的网格收敛性验证结果见表5和表6。网格收敛率RG小于1，说明KT的数值模拟结果满足单调收敛。UG（网格不确定度）为2.31%SG1（网格1尺度下的数值模拟结果）而δ*（数值模拟误差的估计）为1.4%SG1，同时还对UGC（修正的网格不确定度）和SC（修正的数值结果）进行了计算。UGC为0.91%SG1而SC为0.1071SG1。此外，分别对数值模拟结果和修正结果进行了确认分析，结果见表7。由表中结果可知 |E|

表5 以KT为对象的单桨敞水数值模拟网格收敛性验证（网格1的百分比）Tab.5 Grid convergence of KT for single propeller in open water(%of finer grid value)

表6 以KT为对象的单桨敞水验证分析（%of SG1）Tab.6 Verification of KT for single propeller in open water(%of SG1)

表7 以KT为对象的单桨敞水确认分析（%of D）Tab.7 Validation of KT for single propeller in open water(%of D)

2.2 自航不确定度分析

在对自航数值模拟进行不确定度分析中，网格收敛性验证和迭代收敛性验证均使用3 个网格尺度进行。迭代收敛的分析是通过对KT的迭代时历曲线进行分析完成的，迭代时历曲线见图2。内桨KT的迭代不确定度为0.44%D，外桨KT的迭代不确定度为0.78%D。与前述分析方法相同，迭代不确定度用峰峰值的一半占试验值的百分比来表示。在网格2 尺度下，内外桨不确定度分别为0.38%D和0.99%D。网格3 尺度下内外桨不确定度为0.48%D和0.72%D。在自航的数值模拟中，迭代不确定度与网格不确定度相比也为小值，可以忽略。

图2 网格1尺度下自航数值模拟迭代时历曲线Fig.2 Iterative history of KT for self-propulsion with Grid 1

以KT为对象的网格收敛性分析结果见表8 和表9。网格收敛率RG小于1，说明对内外桨来说，网格收敛性均满足单调收敛。内桨的UG为5.06%SG1，δ*为1.72%SG1，UGC为3.34%SG1而SC为0.123 3SG1。外桨的UG为0.64%SG1而δ*为0.35%SG1，UGC为0.3%SG1而SC为0.1041%SG1。此外，分别对数值模拟结果和修正结果进行了确认分析，结果见表10。由表中结果可知 |E|

表8 以KT为对象的自航数值模拟网格收敛性分析（网格1的百分比）Tab.8 Grid convergence of KT for self-propulsion(%of finer grid value)

表9 以KT为对象的自航数值模拟验证分析Tab.9 Verification of KT for self-propulsion(%of SG1)

表10 以KT为对象的自航数值模拟确认分析Tab.10 Validation of KT for self-propulsion(%of D)

3 计算结果及分析

3.1 研究对象

本文研究对象为一艘四桨推进船，螺旋桨为五叶大侧斜桨，数值计算均在模型尺度下进行，模型主要参数见表11，船模及螺旋桨外形见图3。

表11 船模和螺旋桨参数Tab.11 Parameters of ship and propeller

图3 船模及螺旋桨模型三维曲面图Fig.3 3D figure of ship hull and propeller

3.2 单桨敞水计算

本文采用推力实效伴流对四桨伴流场进行分析，故首先进行了螺旋桨敞水计算，敞水性征曲线见图4。

图4 单桨敞水性征曲线Fig.4 Hydrodynamics performance of single propeller in open water

3.3 多桨干扰计算

为了研究四桨船内外桨负荷分配差产生原因，本文对该模型分别进行了五个工况的计算，工况见表12。

表12 工况表Tab.12 Working conditions

工况五为船后无桨拖航，该工况下内外桨桨盘0.8倍半径处伴流分数分布见图5。由图可见，內桨伴流分数大于外桨，说明內桨负荷大于外桨，这与工况一所得出的结论是一致的。常规的单桨船桨盘处伴流分数曲线一般都呈现出U 形，且曲线在整个圆周上变化较为平缓，而图5 中内外桨伴流分数在15°和315°处均存在较大的突变，这是由螺旋桨前端的轴支架对流场的干扰引起的。除受轴支架影响的部分以外，外桨其他部分伴流分数变化不大，较为平均；而內桨伴流分数曲线则有多个拐点，呈现出明显的不均匀性，整个曲线变化较大，说明內桨桨盘处流场较为紊乱。

图5 桨盘处伴流分数曲线Fig.5 Wake fraction on propeller plane

各工况下内外桨负荷用推力实效伴流分数来表征，计算结果见图6。由图可知：（1）工况一为船后四桨同时运转，该工况下內桨负荷大于外桨，且与单桨在敞水中的负荷相比，內桨在船后运转时负荷增大，外桨在船后运转时负荷基本保持不变；（2）工况二、三分别为内外桨单独在船后运转，受船体外形影响，螺旋桨在船后处于非均匀流中，且由于内外桨在船后位置不同，其所处的流场环境也不同，所以内外桨分别单独在船后运转时负荷较单桨敞水时增加，且外桨增幅大于內桨；（3）工况四为四桨在敞水中运转，在该计算模型中，内外桨在敞水中运转时就有负荷差的存在，即内外桨在敞水中互相干扰，导致內桨负荷增大，外桨负荷减小；（4）由前述可知，四桨船的内外桨负荷差是由船体外形和内外桨间干扰产生的，但这两种影响因素的线性叠加结果与工况一（四桨同时在船后运转）的结果并不相等，说明这两种因素之间还存在耦合作用。

图6 不同工况下的伴流分数Fig.6 Wake fraction of differenct cases

3.4 三类伴流的成因

为叙述方便，将上述三种因素的影响归结为三类伴流：原生伴流、干扰伴流和次生伴流。三类伴流之和为总伴流。各伴流的计算方法如下：总伴流为工况一所得到的伴流分数；原生伴流为工况二和工况三的结果；干扰伴流为工况四所得到的结果；次生伴流为总伴流减去原生伴流和干扰伴流。

原生伴流为船体形状对螺旋桨的影响，其与单桨船的伴流类似；干扰伴流为内外桨间直接干扰，即敞水中内外桨的干扰影响；次生伴流为上述两种因素的耦合作用，即内外桨间干扰作用受船体形状影响后的合成，其计算式为

原生伴流与单桨船伴流类似，为船体尾流对螺旋桨的影响，主要由船体形状决定。该计算模型中，內外桨原生伴流均为正，且內桨原生伴流小于外桨原生伴流。

干扰伴流表征的是内外桨同时在敞水中运转时互相之间产生的影响。该计算模型中，內桨干扰伴流为正，外桨干扰伴流为负。图7 为螺旋桨尾流中轴向速度分布，该图最早由Hamill 和Johnston 在1993 年提出[16]，由于受到桨毂的阻碍作用，螺旋桨尾流可以分为两个区域：发展区和完成区。完成区一般在螺旋桨后3 倍直径以外，在该区域中，轴向速度分布在螺旋桨直径范围内几乎不变，而在直径范围以外其轴向速度迅速减小；而在发展区中，螺旋桨轴向速度分布几乎是对称的。对于本文的研究对象，內桨处于外桨的尾流完成区中。

图7 螺旋桨尾流中轴向速度分布区域的示意图[16]Fig.7 Schematic view of a propeller jet showing two zones of flow and efflux velocity distribution[16]

内外桨同时在敞水中运转时流场中伴流分数的等高线见图8，图中流体由左向右流动，左侧为外前桨，右侧为内后桨。由图中可以看出內桨前端伴流分数均为正，说明內桨处于外桨尾流的完成区中。外桨处伴流分数为负，说明内后桨对其前端的流场有抽吸作用，使外桨处流速加快，从而导致外桨伴流分数为负，负荷减小。

图8 四桨敞水伴流分数等高线Fig.8 Contour map of wake fraction of four propellers in open water

次生伴流为原生伴流和干扰伴流的耦合作用，原生伴流和干扰伴流都是单一因素对螺旋桨的影响，原生伴流为船体形状的影响，干扰伴流是桨间的互相干扰，但二者之和与总伴流的数值并不相等，说明二者之间还存在耦合作用。图9为四桨敞水流线图，图10为四桨在船后运转时的流线图，图中流体由左向右流动，左侧为外前桨，右侧为内后桨。由图8 和图9 可知，内外桨在敞水中运转时，二者之间产生了互相干扰，但流体流经外前桨后并不直接进入內桨的桨盘范围。由图10 可以看出，流线在流经外桨后发生偏转，进入內桨桨盘范围，这与四桨在敞水中的情况是不同的，这是原生伴流和干扰伴流的耦合作用造成的。

图9 四桨敞水流线图Fig.9 Streamlines of four propellers in open water

图10 四桨拖航流线图Fig.10 Streamlines of towing with four propellers

为了量化三种伴流对螺旋桨负荷的影响，以总伴流为基准，计算各伴流占总伴流的百分比。由于外桨的次生伴流和干扰伴流均为负值，故在计算外桨的三类伴流占总伴流的百分比时也以內桨的总伴流分数作为基准，三种伴流占总伴流的百分比见图11。由图11 可知，该船的原生伴流、次生伴流和干扰伴流均为同一数量级，均不可忽略，且内外桨原生伴流差距并不明显，造成内外桨负荷差的原因主要是次生伴流和干扰伴流，內桨的次生伴流和干扰伴流为正，而外桨的次生伴流和干扰伴流为负，所以在对四桨船进行设计时应主要考虑这两类伴流的影响。

图11 三种伴流占总伴流的百分比Fig.11 Percentages of three wakes

4 结 语

本文使用CFD 方法对一艘四桨船内外桨负荷分配问题进行研究。对四桨敞水、內桨在船后单独运转、外桨在船后单独运转、四桨同时在船后运转等工况进行了数值计算，结果表明：（1）该四桨船內桨负荷大于外桨；（2）四桨船内外桨负荷差由原生伴流、次生伴流和干扰伴流共同作用形成；（3）原生伴流、次生伴流和干扰伴流均为同一数量级，在四桨船推进器设计中应该同时考虑三个方面的因素。