超大型浮体柔性连接器极限强度模型试验研究

陆 晔，滕 蓓，王新宇，陈彧超，祁恩荣，张 浩

（1.中国船舶科学研究中心，江苏无锡 214082；2.江苏省无锡交通高等职业技术学校，江苏无锡 214151；3.上海船舶研究设计院，上海 201203）

0 引 言

海洋超大型浮体是一种由多个构型尺寸相同或类似的半潜式浮式结构物通过具有特定刚度连接器组成的多模块浮体系统，由于超大型浮体结构庞大，并且长期漂浮在海上，不可避免地会遭到恶劣海况。即使停泊在泻湖内，由于浅水以及非均匀海底地形的影响，超大型浮体结构仍然需要面临巨大的载荷。而连接器作为超大型浮体最基本、最关键的连接设备，也是最为薄弱的环节，当环境荷载大于连接器的设计荷载时，连接器将会发生局部破坏从而导致超大型浮体整体结构失效。为保证连接器的结构安全性，同时保证超大型浮体的完整性，需要评估超大型浮体连接器的极限承载能力。一般来说，超大型浮体的连接器采用铰接式柔性连接方式，通过填充柔性材料达到调节连接器刚度和降低载荷的作用，而铰接式连接方式和柔性材料引入了力学分析的非线性问题，增加了连接器结构极限强度评估的难度。

针对海洋超大型浮体，吴有生[1]首次提出三维线性水弹性理论，研究了弹性连接多刚体模块系统的流固耦合问题，得到了结构在不同浪向角下的运动和变形以及连接件动力响应[2]；Ertekin 等[3]和Riggs 等[4]利用三维势流理论和格林函数法并考虑了刚体模块间水动力相互影响，计算了移动海上基地单模块的运动和连接器载荷，并比较了5个模块不相连、柔性连接以及刚性连接时的运动和连接器载荷；余澜[5]分析了移动海上基地模块间相互作用力、连接器刚度、浪向角、海况对模块运动和连接器载荷的影响；祁恩荣等[6]采用刚性模块柔性连接器模型，基于三维势流理论计算近岛礁浮体水动力，从而得到连接器的动力响应；祁恩荣等[7]还设计了柔性连接器模型，通过不同幅值和载荷组合的连接器静态拉伸和压缩试验，研究了超大型浮体连接器的刚度特性，探讨了组合载荷对连接器刚度的影响；张波等[8]计算了由不同数量半潜式模块组成的海上移动基地系统在规则波和不规则波下的水动力响应和连接器动力响应；刘超等[9]比较了3种不同模型在7级海况作用下的连接器动力响应，探讨了浅水效应对连接器动力特性的影响。上述工作主要集中在超大型浮体连接器外载荷分析方面，提出了重要的理论和实践方法，甚至通过试验来验证连接器的动响应。而由于连接器的构型和设计难以确定，在确定性载荷下的连接器内力计算工作并不多。朱璇等[10]提出了一种柔性连接器的形式，建立连接器的有限元模型进行非线性分析；陆晔等[11-12]针对超大型浮体的载荷特性设计了铰接式柔性连接器，通过耳环数量、销轴结构形式等各种优化，确立了空心变截面圆柱体销轴单耳加装尼龙套筒的形式；张浩等[13]研究了带有柔性夹层连接器的力学特性，明确了柔性夹层对连接器的刚度和应力变化的影响。

本文以横向浮筒式的超大型浮体为研究对象，结合连接器动响应特点，设计并开展了柔性连接器极限强度模型试验，试验目的如下：

（1）建立柔性连接器极限强度模型试验方法，掌握相关试验测量技术和数据分析方法，为鉴定柔性连接器承载能力提供有效手段；

（2）获得柔性连接器在工作载荷下的结构应力分布和变形情况，了解各构件的承载能力，为优化柔性连接器设计方案提供依据；

（3）揭示柔性连接器结构的失效模式，获得柔性连接器的极限强度，为验证柔性连接器的极限强度评估方法提供依据。

本文通过对模型载荷、结构应力和变形等测量数据的分析，了解柔性连接器结构应力分布和变形情况，给出柔性连接器的结构失效模式和极限强度，为验证柔性连接器的极限强度评估方法和优化柔性连接器的设计方案提供依据。

1 试验对象

1.1 试验对象原型

超大型浮体主尺度见表1，模块间的连接器安装位置如图1 所示，连接器中心位置布置在立柱中心和主浮体高度重心位置，即距基线24 m，距浮体宽度中心线29 m位置。

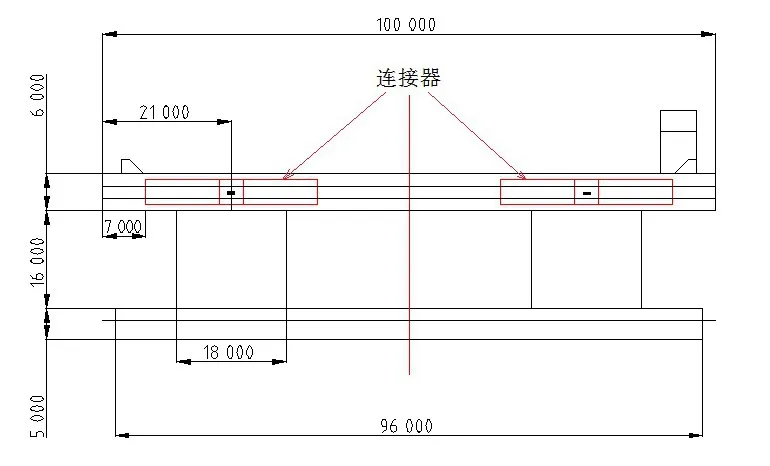
图1 连接器布置位置Fig.1 Connector locations

表1 超大型浮体主尺度Tab.1 Main parameters of VLFS

以五模块横向浮筒式超大型浮体为研究对象，开展了铰接式连接器载荷与响应研究，不同浪向角下连接器受力如图2所示，横坐标是浪向角（°），纵坐标是连接器载荷（N）。当浪向角小于60°时，连接器载荷和模块运动响应较小，纵向载荷Fx小于40 MN，可作为连接器的工作载荷；浪向角在60°～90°时，连接器载荷和模块运动响应出现峰值，最大纵向载荷可达工作载荷的近3 倍，是设计中应该避免的极端载荷。

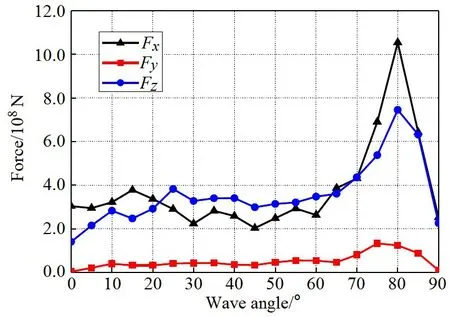
图2 不同浪向角下连接器受力Fig.2 Forces of connectors at different wave angles

根据铰接式连接器载荷与响应研究结果，设计了如图3所示的铰接式连接器，连接器总长为4.0 m，宽为2.4 m，高为2.4 m，主要由单耳、双耳、基座、环肋加强圆管轴和尼龙柔性夹层构成，主要参数如表1所示。

图3 超大型浮体柔性连接器原型三视图及三维图Fig.3 3-view diagram and 3D image of VLFS connector prototype

柔性夹层布置在单耳和圆管轴之间，采用尼龙66 材料（弹性模量为8.3 GPa，泊松比为0.405），其余构件采用高强度钢（弹性模量为206 GPa，屈服强度为315 MPa，泊松比为0.3）。采用柔性夹层不仅可以减小冲击载荷引起的损伤，而且还可以调节模块间相对运动的频率，以错开波浪谱中能量峰值频率，从而减小模块间相对运动和连接器载荷。圆管轴内表面在单、双耳之间布置加强环肋，采用这样的结构型式一方面是为了减轻连接器重量，另一方面也是为了在极限状态时连接器先于模块和基座破坏。

1.2 试验对象模型

综合考虑超大型浮体柔性连接器的结构特点、加工工艺、加载装置等因素，选择模型与原型的缩尺比为1:10，连接器缩尺后主要参数见表2。连接器装配模型和有限元模型如图4 所示，将基座与加载装置合为一体，通过后部中心螺杆与液压装置相连。考虑到加工便利和节约成本，材料选用普通钢（名义屈服强度为235 MPa，实测屈服强度约为300 MPa）。

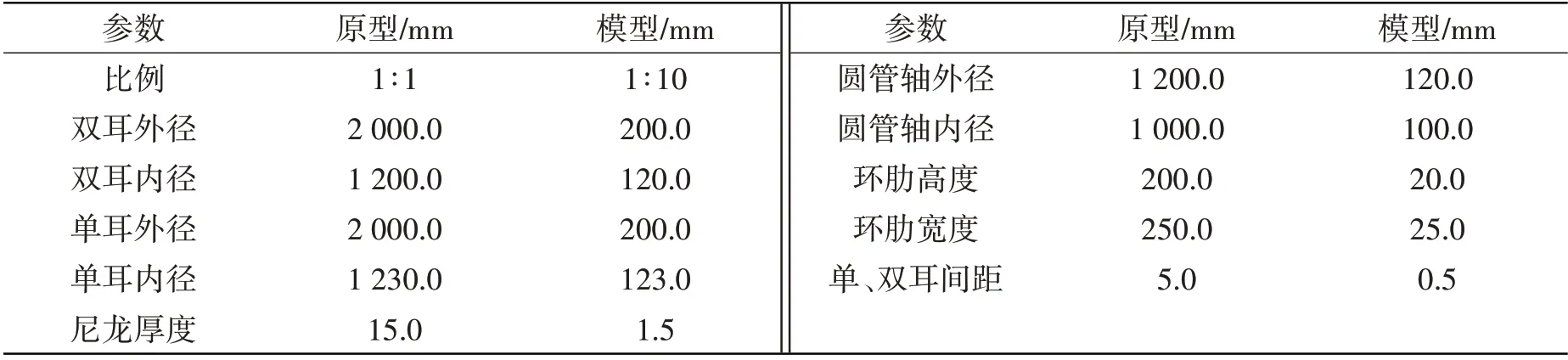
表2 超大型浮体柔性连接器原型和缩比模型主要参数Tab.2 Main parameters of VLFS flexible connector prototype and scaled model

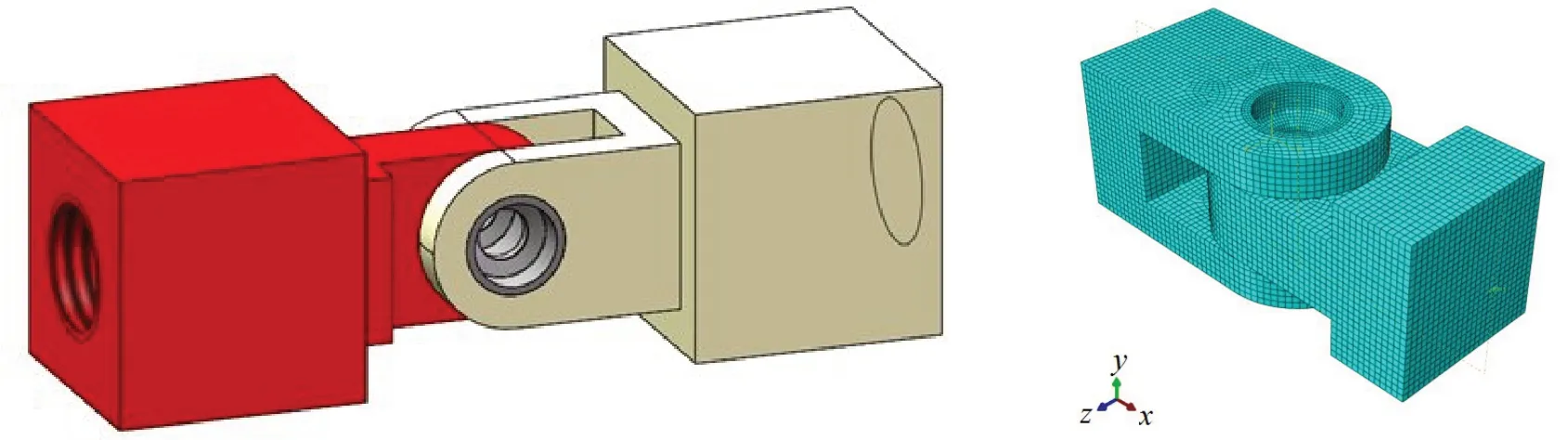
图4 超大型浮体柔性连接器试验模型三维效果图（包括基座与加载装置）Fig.4 3D renderings of the test model of the flexible connector for VLFS (including base and loading device)

2 试验内容和测点布置

2.1 试验内容

本试验主要研究在纵向极端载荷作用下柔性连接器的极限强度，试验内容主要包括以下几个方面：

（1）材料力学性能试验

将模型同批次的钢材制成拉伸试件，进行材料力学性能试验，测量试件应力和变形，获得材料的弹性模量和屈服强度。

（2）弹性试验

在材料弹性范围内作三次纵向加载，最大载荷为500 kN，加载步长为100 kN。检验测量系统和加载装置的可靠性，测量模型载荷、应力和变形，获得模型应力分布和载荷-位移曲线。

（3）极限破坏试验

进行极限破坏试验，在载荷小于1 300 kN 时，加载步长为100 kN；在载荷大于1 300 kN 时，加载步长为50 kN，直至连接器试验模型发生极限破坏。测量试验模型载荷、应力和变形，获得模型极限失效模式和极限强度。

2.2 测点布置

本文采用ABAQUS软件进行连接器原型强度计算，其中，连接器的单耳和双耳与销轴分别采用面接触方式建模，柔性夹层与单耳内侧面以及销轴采用面接触方式建模。整个模型共计18 499个节点，15 888个8节点的C3D8R单元。在模型的左侧双耳基座面施加固定约束，在右端单耳基座施加X向单向载荷40 MN，连接器原型应力计算结果如图5所示。

图5 连接器原型Fig.5 Prototypes of the connector

根据有限元应力结果，给出了如图6 和表3 所示的模型试验测点布置，其中三向应变片12 个、单向片1 个，共计13 个测点和37 个通道。由于空心变截面圆管轴与双耳及单耳耳面接触并传递载荷，故测点均在圆管轴的内壁。

表3 超大型浮体柔性连接器极限强度模型试验测点布置Tab.3 Measuring point distributions for ultimate strength model test of the flexible connector for VLFS

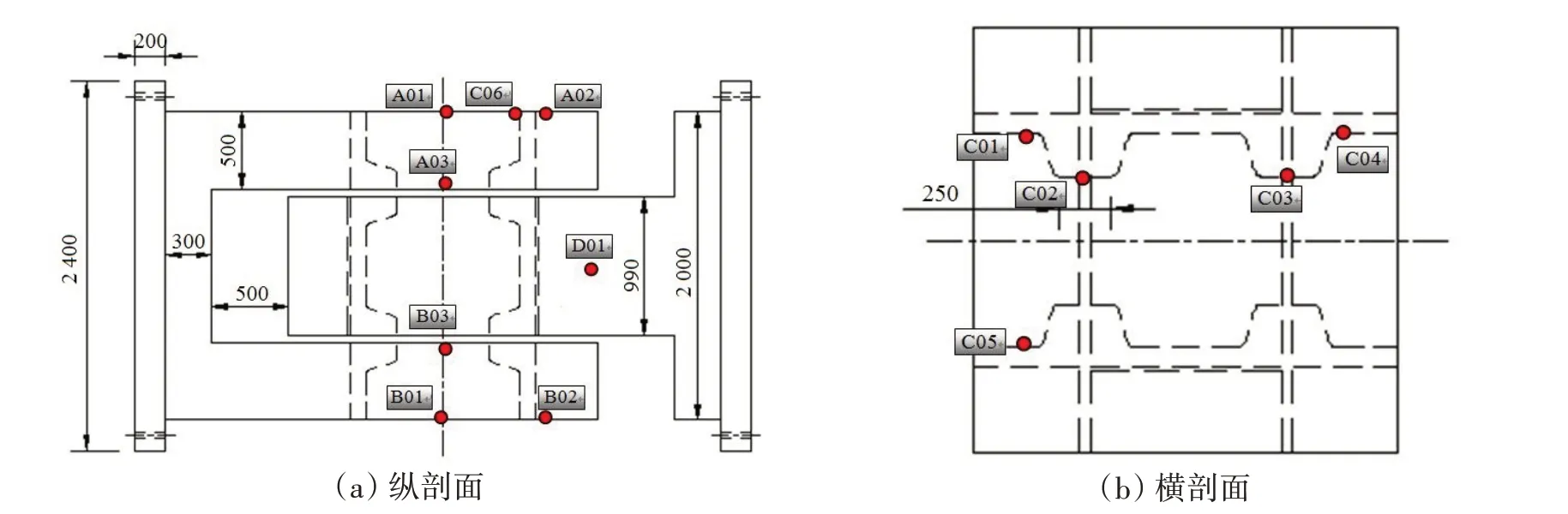
图6 测点布置Fig.6 Measuring point distributions

2.3 试验过程

按照模型试验大纲的要求进行试验模型及加载装置的加工，完成测点布置等准备工作。借助工装，将连接器试验模型装配在6 000 kN 的结构试验平台上，如图7 所示，连接应变传感器，调试加载装置，布放位移传感器等。试验过程中，在连接器模型单耳端部施加拉伸载荷，在双耳端部施加固支约束。

图7 试验加载装置Fig.7 Test loading device

连接器极限强度模型试验结束后对试验模型屈服破坏情况进行检查。图8为连接器极限强度试验结束后的变形情况，圆管轴已经发生明显的塑形弯曲变形，双耳向外扩张严重，单耳塑形变形并不明显，同时尼龙发生一定程度的撕裂。通过对采集数据的读取，发现测量数据记录完整，各测点信号正常，可以确定此次试验成功。

图8 连接器变形图Fig.8 Deformation of the connector after test

3 模型试验结果分析

3.1 试验模型材料性能

试验模型试验段采用了Q235钢，因此加工与模型材料同一生产批次的10 mm厚度板材试件1只，利用材料试验机得到各试件应力应变关系，应力应变曲线如图9所示。

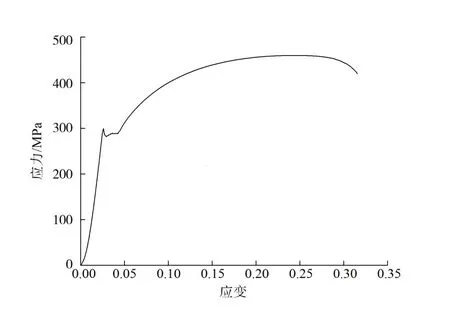
图9 材料应力应变曲线Fig.9 Stress-strain curve

3.2 试验模型单双耳极限强度试验应变测量及分析

结合连接器模型中单双耳在破坏试验时的应变测量结果可知，双耳变形量要大于单耳，且双耳主要变形是沿轴向的拉伸变形，其中最大应变位于A03号和B03号测点附近。在轴向荷载小于1 200 kN时，双耳的应变增加幅度较为稳定。当轴向荷载达到1 200 kN时，双耳的应变明显增大，如图10（a）所示。

3.3 试验模型圆管轴应变测量及分析

根据连接器模型中圆管轴在破坏试验时的应变测量结果可知，圆管轴的应变最大，其中最大应变位于C06和C02号测点附近。在轴向荷载小于1 200 kN时，圆管轴的应变增加幅度较为稳定。当轴向荷载达到1 200 kN时，双耳的应变明显增大，如图10（b）所示。

图10 通道荷载应变曲线Fig.10 Load-strain curves of partial channels

3.4 试验结果与非线性有限元计算对比

根据试验模型实测的材料性能和尺寸，对其数值模型进行调整，再次进行材料和几何非线性多面接触计算，获得模型在破坏前的变形情况，失效模式的等效应力分布如图11所示。

图11 柔性连接器模型失效模式等效应力分布Fig.11 Equivalent stress distribution of failure mode of flexible connector model

图12给出了试验和计算的极限破坏的载荷-位移曲线，1 000 kN载荷步以前，位移-荷载曲线呈近似线性变化规律；1 000 kN 以后，连接器的非线性力学特性明显；当荷载增加至2 000 kN 时，连接器发生破坏，油缸卸载，连接器模型极限强度为2 000 kN。计算结果的破坏形式与试验结果基本一致，计算得到连接器模型的极限强度为1 987 kN，误差为0.65%，与试验结果吻合。

图12 柔性连接器载荷位移曲线对比Fig.12 Load-displacement curve comparison between calculations and test of flexible connectors

4 结 论

根据试验大纲的要求，通过精心和细致的试验准备，以及对试验数据的分析，可以认为连接器极限强度模型试验在模型设计、模型加工、加载方案和加载装置设计、应变测量等各方面的工作都是成功的，试验测量数据是正确、有效和可靠的，试验数据分析结果可为验证真实连接器极限强度计算方法提供试验依据。

从超大型浮体柔性连接器极限强度模型试验中主要得到了如下结论：

（1）基于刚性模块柔性连接模型计算五模块横向下浮筒式超大型浮式结构物的动力响应，获得连接器的工作载荷和极限载荷，根据连接形式以及连接器结构特点，进行了超大型浮体柔性连接器结构模型设计和极限强度试验，并与非线性有限元法在失效模式和极限强度两方面进行了很好的比较验证。一方面，这种空心变截面销轴很好地抵抗了模块之间拉压过程中产生的剪切力；另一方面，在测点布置上提供了足够的空间用以布置应变片来测试连接器的应变情况。总体来说，试验模型和数值计算有着相同的失效模式，即双耳内径扩大外翻张开，单耳内径扩大，内壁出现塑性变形，在极限强度的极值预报上两者也吻合较好，试验结果很好地证明了模型的设计准确性和极限强度分析方法的有效性。

（2）连接器极限强度模型试验共布置了37个应变测点，提供了大量应变测量结果，可为验证和完善连接器极限强度计算方法提供试验依据。其中，由于双耳结构左右对称，并且拉力经过双耳中心，因此对称位置测试点的应变具有同步性，并且在失效状态下也保持接近状态，而数值上的差距主要来源于人工粘贴应变片的位置误差以及受拉时载荷的偏移。另外，圆管轴在受拉剪切变形后，环肋顶部及内侧边有最大变形量，这是因为圆管轴无法再承载极限强度后最终的失效模式导致的挤压变形量，为工程上使用该类型的圆管轴提供了设计思路。