基于模糊PID的船模航向控制研究

石磊， 夏召丹， 王志南， 王大建， 杨素军

(1.中国船舶工业集团公司， 第七○八研究所， 上海 200011；2.上海市船舶工程重点实验室， 上海 200011)

0 引言

我国在上世纪七十年代首次使用船模技术，此技术的使用能够协助研究人员直观的分析水力学问题。人们将船模技术大量使用在航道管理与船舶航向控制问题中，这对我国船模技术的发展存在积极作用。很多科研部门根据船模控制运动的原理，使用计算机编程仿真模拟船模运行，以此通过可视化的效果分析差异船型船模运行问题，并设置不同船型船模的控制方法。

船模航向控制中，经典控制理论与自适应控制理论使用的较多，因为船模航行时，航模的航速、装载状态、外界环境影响条件都是按照实际船舶的具体情况所模拟，具有相似性，所以，此时船模航行控制将出现显著的水动力非线性问题，致使传统PID自动舵操舵难度增加，航机损耗变大，参数整定难度也变大，自适应变差，控制效果与稳定性将大受影响[1]。本文提出基于模糊PID的船模航向控制方法，该方法基于神经网络的自学习性、自适应性优势，对模糊PID参数进行改进，使用模糊规则整体运算PID控制误差，提高网络收敛效率，完成PID参数高效整定，实现船模航向精准控制。

1 基于模糊PID的船模航向控制方法

1.1 基于多维关键数据挖掘的船模航向控制参量与核心数据挖掘方法

设置船模航行时的位姿扰动向量q(h)与航行目标路径姿态z(h)之间的关联度特征分布函数Aj(h)：

(1)

设置船模航行的目标初始状态a(0)均值是a0，方差设成Q0。采集船模航行位置参量Ω(h)，获取侧向偏转角a(h+1)、速度矢量信息rj(h)：

a(h+1)=B(h)a(h)+Ω(h)q(h)

(2)

rj(h)=Ω(h)a(h)+z(h)

(3)

其中，a(h)、B(h)分别是第h次采样时刻的侧向偏转角、状态转移矩阵，Ω(h)是第h次采样时刻的船模位置参量。

使用自适应信息融合方法，获取船模航行过程中核心数据信息：

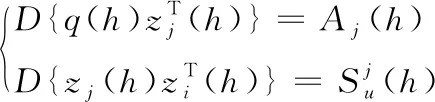
(4)

(5)

1.2 基于BP算法的船模航向模糊PID控制方法

挖掘船模航行位置信息、侧向偏转角信息、速度信息，了解船模目前航行状态之后，本文使用基于BP算法的船模航向模糊PID控制方法，实现船模航向控制。

1.2.1 控制器设计

PID控制器可实现船模航向闭环控制，但需要在线整定比例系数HP、积分系数HI、微分系数HD。为了自适应调整PID控制器参数，优化PID控制器的性能指标，为此本文引入BP神经网络[2]。BP神经网络输出层神经元的输出状态和PID控制器的HP、HI、HD3个参数相呼应，在自学习之后，调节加权系数，便可在最优控制律条件下实现HP、HI、HD寻优，实现船模航向最优控制[3-5]。

经典增量式数字PID控制方法：

v(h)=v(h-1)+Δv(h)

(6)

其中，v(h)、v(h-1)、Δv(h)分别是第h次采样时刻的输出控制量、第h+1次采样时刻的输出控制量、第h次采样时刻的输出控制量均值[16]。

Δv(h)=HP(f(h)-f(h-1)+HIf(h)+

HD(f(h)-2f(h-1)+f(h-2))

(7)

其中，f(h)、f(h-1)、f(h-2)分别是第h次采样时刻输入的HP、HI、HD误差、第h-1次采样时刻输入的误差、第h-2次采样时刻输入的误差。

把HP、HI、HD设成船模航向控制的可调系数时，把式(7)变换成：

v(h)=g[v(h-1),HP,HI,HD,f(h),f(h-1),f(h-2)]

(8)

其中,g[·]是激活函数。

1.2.2 误差的归一化

第h次采样时刻输入的HP、HI、HD误差是f(h)=s(h)-x(h)，s(h)、x(h)分别是采样值与实际值，则误差归一化方法是f(h)/s(h)[7]。基于BP神经网络的PID控制器结构图见图1。

图1 基于BP神经网络的PID控制器结构图

1.2.3 网络结构和前向运算

假定BP神经网络具有三层网络[8]，结构详情见图2。

(9)

其中，N是输入变量的数量，Fh-i是船模航向角。

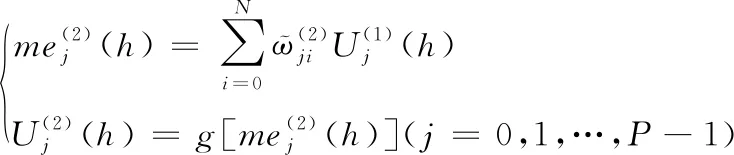
(10)

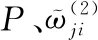
(11)

1.2.4 控制流程设计

(2)采样获取s(h)、x(h)，运算获取f(h)；

(3)将f(h)实施归档模糊处理，设为神经网络结构的输入[10]；

(4)使用式(9)～式(11)运算神经网络结构的每层神经元输入、输出值，运算获取输出层的输出值，调节PID控制器的HP、HI、HD；

(5)使用式(7)运算PID控制器的控制输出v(h)；

(12)

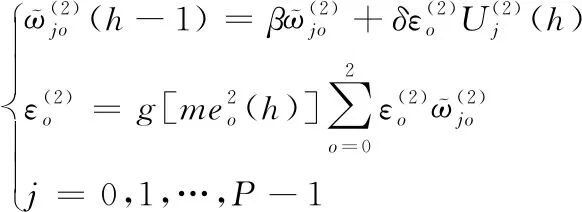
(13)

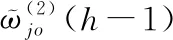
(8)跳转至第2步骤。

流程如图3所示。

图3 控制流程图

2 实验结果析

为测试本文方法的使用效果，在MATLAB仿真软件中，对本文方法的使用效果进行仿真测试。测试本文方法在控制船模航向之前，对船模航行位置信息、侧向偏转角信息、速度信息的挖掘效果，船模航行位置信息、侧向偏转角信息、速度信息的挖掘效果直接影响到船模航向控制效果。以查全率、查准率为测试内容，查全率(recall ratio)的表达式：

(14)

式中，ϑa是本文方法对船模航行位置信息、侧向偏转角信息、速度信息的挖掘量，ϑb是实际船模航行位置信息、侧向偏转角信息、速度信息量。

查准率(Precision)的表达式：

(15)

其中ϑc是本文方法挖掘的船模航行信息总量。

本文方法对船模航行位置信息、侧向偏转角信息、速度信息的查全率、查准率测试结果如图4所示。分析图4可知，多次测试中，本文方法对船模航行位置信息、侧向偏转角信息、速度信息的查全率、查准率都大于0.98，验证了本文方法可高精度、全方位挖掘船模航行位置信息、侧向偏转角信息、速度信息。

(a) 查全率

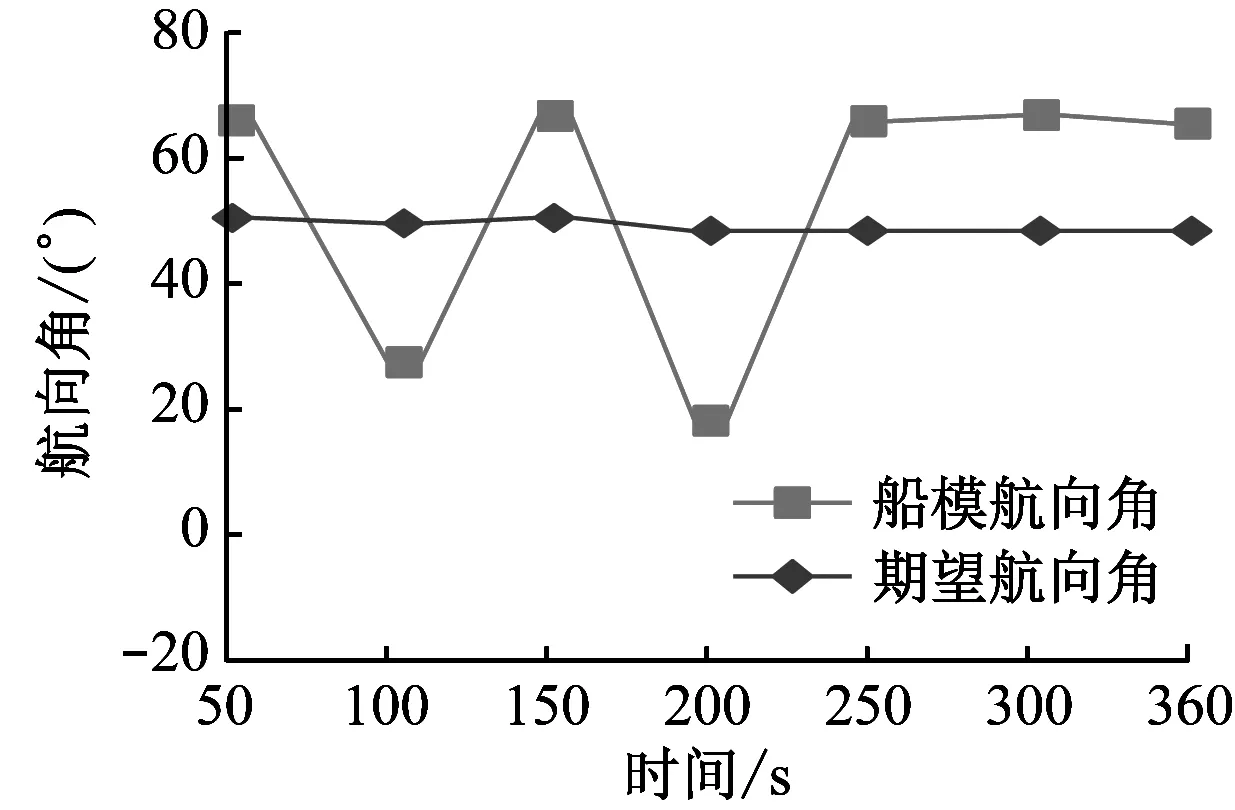
分别模拟船模航行环境，在航行环境有干扰、无干扰的条件中，测试本文方法控制前后，船模的航向控制效果，测试结果如图5、图6所示。无干扰是指静水环境，有干扰是指实验中模拟的风浪环境。分析图5、图6可知，在有干扰、无干扰的条件中，本文方法控制前，船模的航向角与期望航向角存在偏差，船模未能按照期望航向进行航行，本文方法控制后，船模的航向角与期望航向角一致，船模可以按照期望航向进行航行。由此可证，本文方法能够有效控制船模按照预期航向进行航行。

图5 有干扰条件中本文方法控制效果

图6 无干扰条件中本文方法控制效果

测试本文方法控制前后，船模的航向控制速度，控制速度主要以船模航向偏离期望航向时，本文方法控制船模再次按照期望航向航行的时间体现。图7是船模航向偏离示意图，本文方法控制速度测试结果如图8所示。分析图8可知，在有干扰、无干扰的条件中，使用本文方法之前，船模按照期望航向角航行时，所需耗时最大值分别超过25 min、15 min；使用本文方法之后，船模按照期望航向角航行时，所需耗时最大值都低于10 min，对比之下，本文方法控制速度最快，能够在最短时间内控制船模按照期望航向航行。

(a) 有干扰

(a) 使用前

3 总结

本文研究基于模糊PID的船模航向控制方法，并在实验中对其使用效果进行了仿真测试，经过测试验证，本文方法能够在控制船模航向之前，全方位、高精度挖掘船模航行位置信息、侧向偏转角信息、速度信息；能够在有干扰、无干扰的条件中，在最短时间内控制船模航向按照期望航向航行，存在可应用性。

但因时间原因，本文方法还处于仿真测试阶段，在后续研究工作中，将会通过实际的航向控制效果对其进行性能测试，逐步优化该方法的不足之处。