基于“惯容—弹簧—阻尼”体系的线谱和宽带一体化隔振器结构综合

张赣波，赵 耀，陈学东

（华中科技大学a.船舶与海洋工程学院；b.机械科学与工程学院，武汉 430074）

0 引 言

机械振动是舰船隐蔽航行状态下低频线谱的主要来源，因此，亟需突破机械振动线谱治理的关键技术[1]。当前，针对线谱隔振技术的研究主要聚焦在混沌隔振和反共振隔振两个方向。混沌隔振基于“强非线性系统在混沌振动状态时具有‘线谱输入，连续宽带谱输出’的特性”这一原理实施线谱重构，将集中于线谱频率的能量分散到连续宽带频率中[2]，但还面临小能量控制、大参数范围、稳定时间、高混沌品质等技术困难和挑战[3]。反共振隔振是基于惯性力和弹性力等值反向形成反共振的原理，将线谱振动能量吸收、转移至储能元件中，最早在直升机旋翼—机身隔振中被采用[4]，隔振器型式也从最初的机械式发展为液压式[5]和液弹式[6]。文献[7]以共振转换器作为舰船推进轴系纵向振动低频线谱的反共振隔振装置，原理样机试验结果表明可有效降低共振线谱。

反共振隔振技术的关键在于引入具有两个独立、自由端点的惯性元件。具有这一动力学特性的惯性元件被定义为“惯容”[8]。其原理是通过传动机构的转换创造惯性元件发生运动耦合的条件，在转换过程中同时产生放大效应，放大惯性元件的视在惯性。目前，已开发的惯容实现结构包括齿轮齿条式、滚珠丝杠式、流体式、液压式等[8-11]，为突破传统“弹簧—阻尼”隔振器结构体系提供条件。文献[12]将惯容引入车辆悬架中，组合得到21 种悬架结构模型，采用双目标优化识别出12 种新型结构性能均优于传统悬架。文献[13-14]在以一个弹簧作为主承载元件的条件下，组合不同元件数量的含惯容隔振器结构模型，采用H2和H∞优化算法推导出最优刚度比和最优阻尼比的解析解，并从响应放大角度与传统动力吸振器进行比较。上述研究都是先针对性地设定不同组合的“惯容—弹簧—阻尼”隔振器结构模型，再分析隔振系统的隔振特性，属于动力学正问题研究。这种正向分析方法存在的问题在于漏解，即具有目标特性的隔振器结构可能不止一种组合。此外，因排列组合的不充分性，具有更优越性能的隔振器结构也可能被遗漏。

舰船工程中的激励源具有复杂性，如浮筏、推进系统等，是典型的连续宽带和离散线谱的混合激励。在单层、双层和浮筏隔振技术普及应用后，宽带振动得到了卓有成效的治理，但不能有效降低线谱强度。而单独针对线谱的反共振隔振技术，宽带隔振效果不佳。从工程需求角度出发，要求降低线谱应兼顾宽带隔振以避免顾此失彼。

本文将惯容引入隔振器结构中，在“惯容—弹簧—阻尼”体系框架下开展隔振器结构综合的逆问题研究。基于机电相似性，将隔振器作为一个机械网络，根据线谱和宽带一体化隔振的技术条件，采用电网络理论综合出满足要求的两种隔振器结构，并进行隔振特性和阻尼影响分析。所综合的两种隔振器结构具有工程可实现性，为线谱和宽带一体化隔振提供了一种被动控制技术途径。

1 惯容基本特性

1.1 惯容的动力学模型

具有两个独立、自由端点的惯性元件称之为惯容，其惯性力与两端点的相对加速度成正比[8]，关系式为

式中，比例系数b为常数，称之为惯质，单位为kg；vi是两端点速度，i= 1,2。

惯容与弹簧和阻尼一样同属于两端点元件，其两端点的加速度是惯性坐标系下的绝对加速度，两端点的绝对加速度之差产生惯容的惯性力。而质量（或惯量）是单端点元件，单端点的加速度就是惯性坐标系下的绝对加速度，直接产生惯性力。惯容和质量的惯性力与加速度的关系描述见图1。从两端点的一般性看，质量元件的另一个端点固定在惯性坐标系的原点，相当于接地的惯容。因此，惯容是更具一般性的惯性元件，而质量是特殊性的惯性元件。

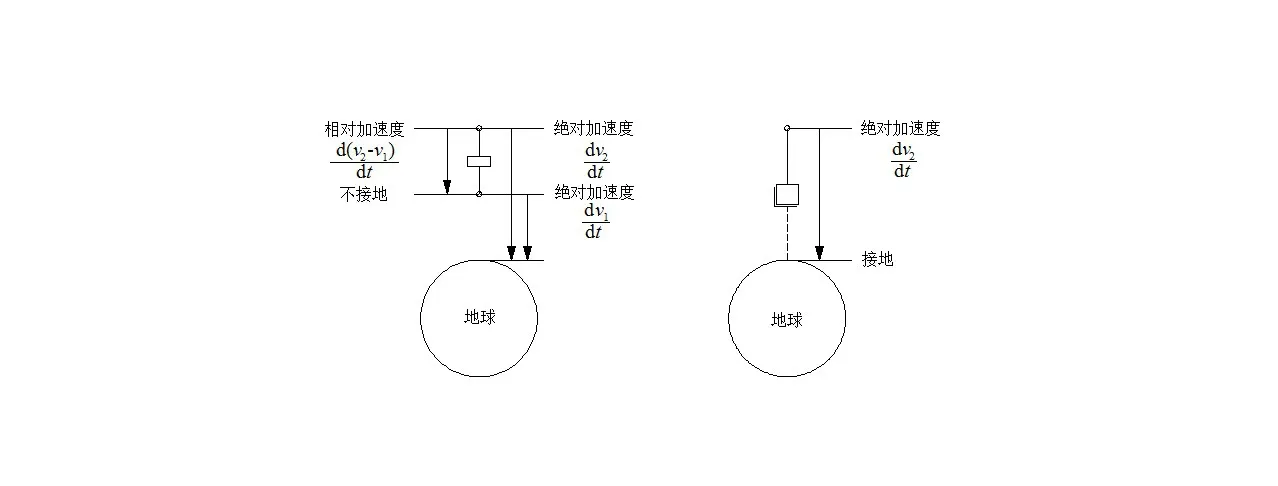
图1 惯容和质量的惯性力与加速度的关系Fig.1 Relationship between inertia force and acceleration of inerter and mass

1.2“惯容—弹簧—阻尼”的匹配关系规律

在惯容被物理实现后，机械系统和电气系统建立起严格相似关系。在“力—电流”第二类机电相似理论中，机械系统的惯容、弹簧、阻尼分别与电气系统的电容、电感、电阻相对应，为机械系统应用成熟的电网络综合理论创造条件。据此，建立如图2 所示的隔振系统机械网络模型。类比电网络，隔振器可看作一个双端接载的无源双口四端网络，输入输出端特征参数以力fi、fo和速度vi、vo表示。输入端负载是被隔振设备阻抗Zm，输出端负载是基础（或基座）阻抗Zf。若隔振器阻抗为Zi，则以机械阻抗表示的隔振系统力传递函数为

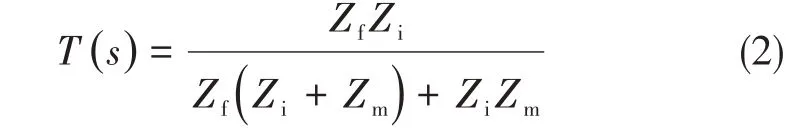
图2 隔振系统的机械网络模型Fig.2 Mechanical network model of vibration isolation system

将惯容、弹簧、阻尼三元件串并联组合成隔振器机械网络模型，共有8种组合方式，如图3所示。

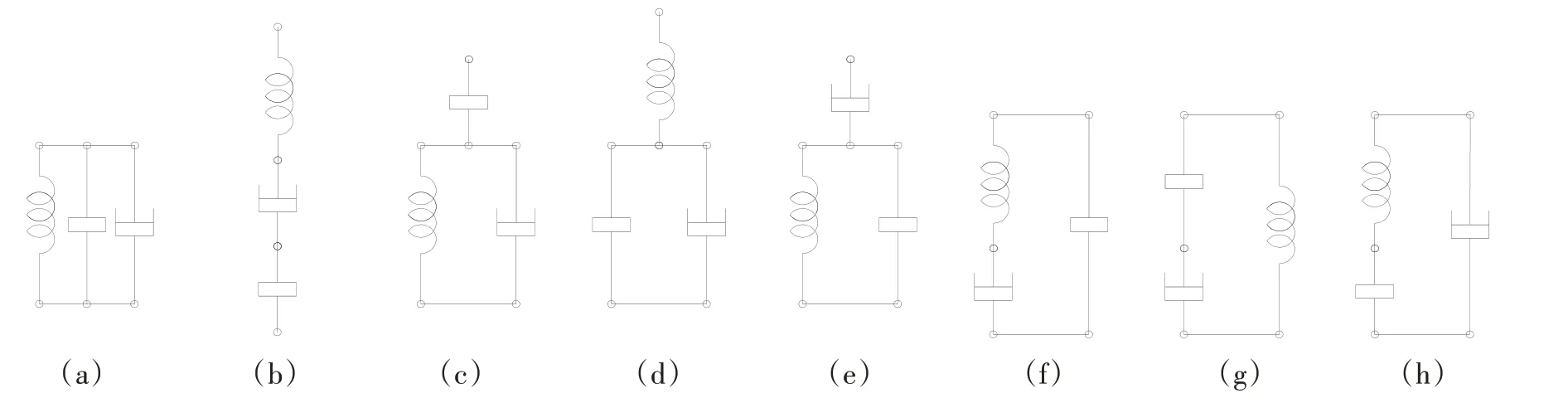
图3 惯容、弹簧、阻尼三元件组合方式Fig.3 Combination types of inerter-spring-damping three elements

根据阻抗的串并联关系式，这8种组合方式的机械阻抗分别为

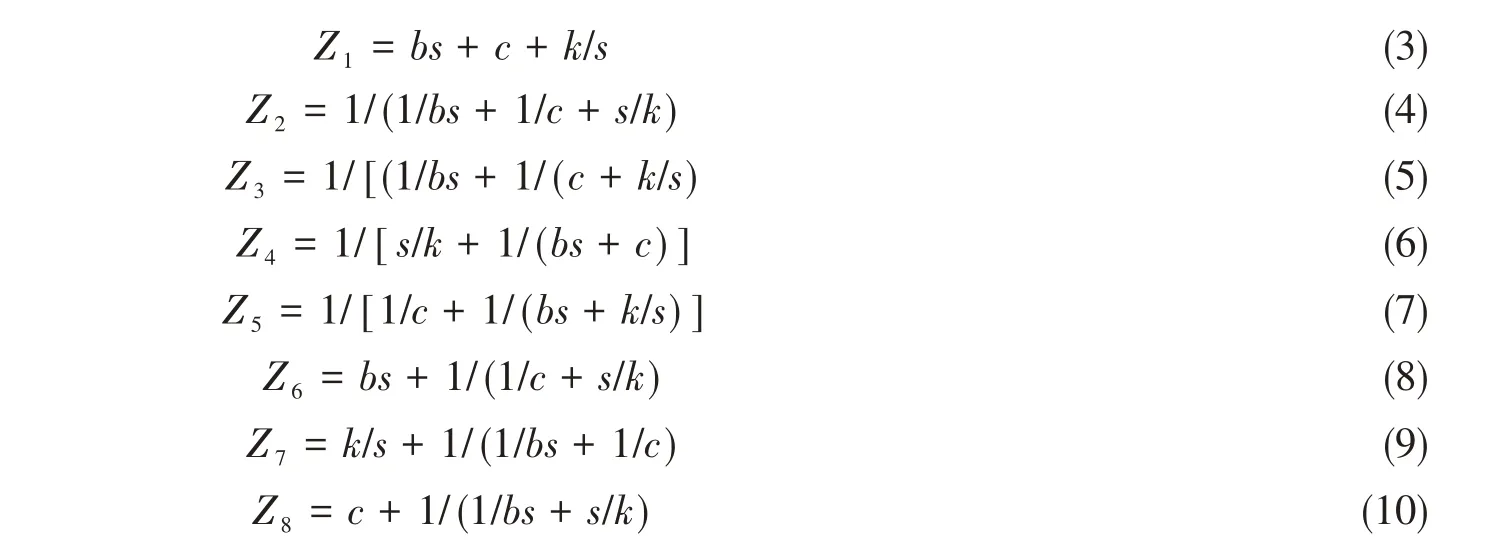
式中，k、c分别为弹簧刚度和阻尼系数，s为复数。

从图4可以总结“惯容—弹簧—阻尼”的匹配关系规律为：反共振的条件是惯容和弹簧并联，如组合方式（a）、（e）；在并联的惯容和弹簧结构中串联阻尼，将破坏反共振的条件，如组合方式（f）、（g）；在串联的惯容和弹簧结构中增加阻尼，都不会出现反共振，如组合方式（b）、（c）、（d）、（h）。

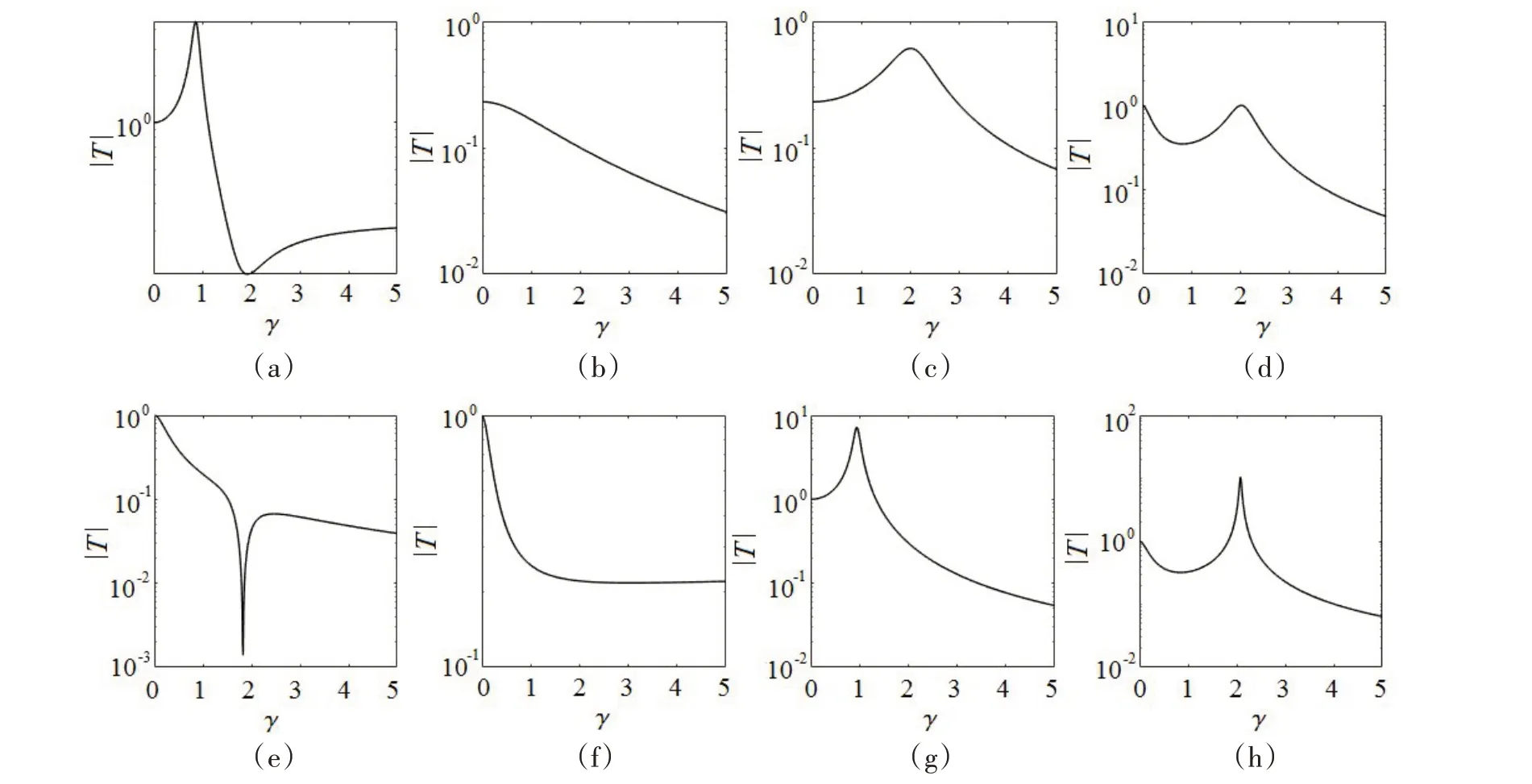
图4 不同组合方式的力传递函数幅频特性Fig.4 Amplitude-frequency characteristics of force transfer function corresponding to different types

2“惯容—弹簧”机械网络综合理论

2.1 线谱和宽带一体化隔振的技术条件

技术条件是指所设定的隔振器机械网络特性要求。在隔振系统分析中，通常以力传递率作为理论分析依据。为此，以力传递特性要求描述线谱和宽带一体化隔振的技术条件。

以反共振隔振作为线谱隔振的技术途径，而宽带隔振则采用传统的隔振技术。反共振隔振的特征反映在力传递函数曲线上是存在陷波的反共振峰，而宽带隔振的特征是在隔振区力传递函数曲线具有一定的衰减斜率，即力传递函数幅值单调递减。

图5展示了单层隔振和动力吸隔振的力传递函数幅频特性。动力吸隔振表现出较好的线谱和宽带一体化隔振特性，在线谱激励频率处出现反共振峰，而在第二阶共振峰之后隔振区的力传递函数曲线与单层隔振的力传递函数曲线趋于重合，具有相同的衰减斜率。根据机械系统的隔振与电气系统的滤波在原理上的相似性，线谱和宽带一体化隔振的技术条件反映在力传递函数曲线上，是在不同频带内具有不同类型的“滤波”特征，如图5所示的低通带、陷波阻带和高阻带。

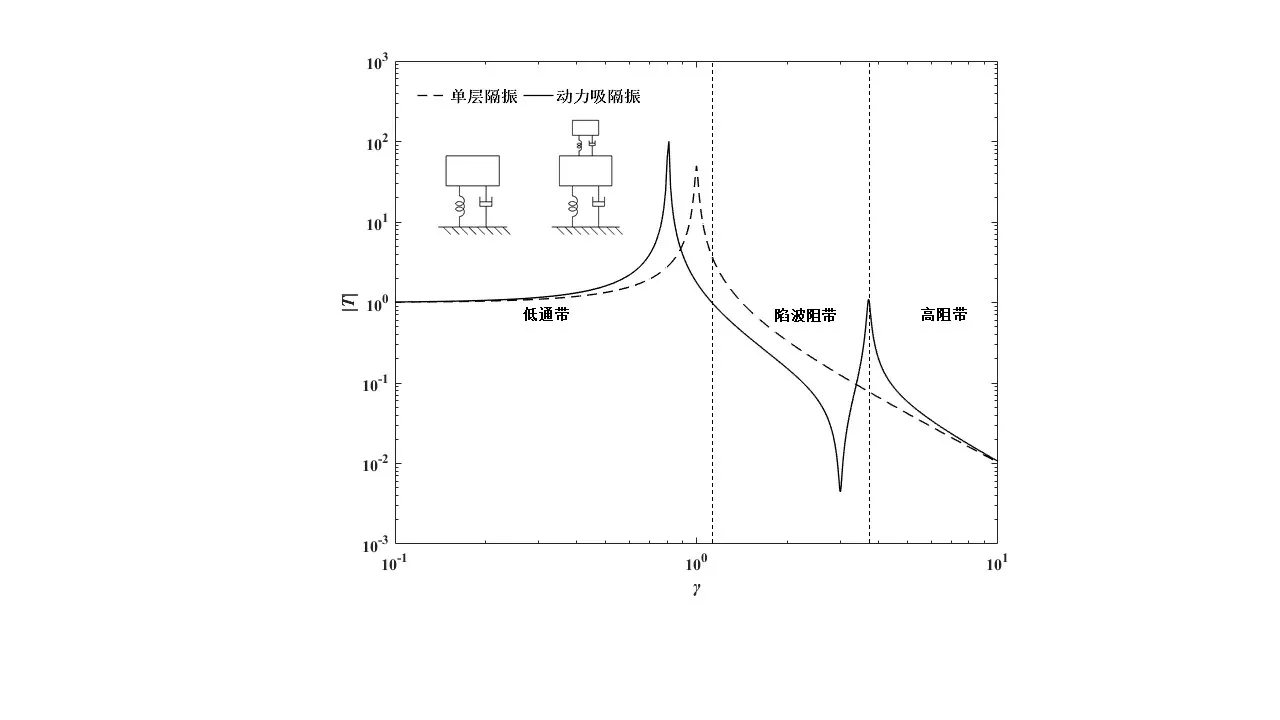
图5 单层隔振和动力吸隔振的力传递函数幅频特性比较Fig.5 Amplitude-frequency characteristics of dimensionless force transfer function between vibration isolation and dynamic vibration absorption

2.2 力传递函数综合方法

在机械系统的基本元件中，阻尼元件不改变机械系统的特性，表现为不影响传递函数曲线的基本特征，其影响局限在共振区和反共振区。故以惯容、弹簧二类元件进行隔振器机械网络综合。

线谱隔振通过反共振实现。类比滤波器原理，滤波器的类型由分子多项式所决定。机械系统的反共振隔振即属于陷波滤波器类型。陷波滤波器的构成要求力传递函数分子是形如b2s2+b0的2 阶多项式。

宽带隔振要求力传递函数分母多项式的阶数高于分子多项式。对于传统隔振器结构，单层隔振系统的分母多项式阶数比分子多项式高2 阶，为使得一体化隔振力传递函数在隔振区的衰减斜率达到单层隔振的下降水平，则一体化隔振力传递函数分母应是形如a4s4+a2s2+a0的4阶多项式。

因此，线谱和宽带一体化隔振的力传递函数的一般形式为

式中，a0、a2、a4、b0、b2都是正的常系数，分母是严格霍尔维茨多项式，仅有s复平面左半平面的根[15]。

假设基础刚性，隔振器机械网络退化为单端接载的双口无源网络，由图2列出方程组：

式中，z11和z21是隔振器机械网络阻抗矩阵的原点和跨点阻抗。对于无源网络，力流无损失，有

z11=z21。

由此推导出隔振器机械网络的力传递函数为

式（13）表明，隔振器机械网络的力传递函数与其阻抗具有严格的对应关系。根据“力—电流”第二类机电相似理论，对于由惯容、弹簧二类元件构成的无源机械网络，z11、z21是关于s的有理正实奇函数[15]。考虑被隔振设备阻抗Zm=ms，进而可推知T(s)是关于s的偶函数，这进一步印证了式（11）的正确性。

令z11=z21=N(s)D(s)，其中，N(s)是分子多项式，D(s)是分母多项式，代入式（13），整理得

根据式（11），在力传递函数分母是4 阶多项式的条件下，D(s)必定是形如a3s3+a1s的3 阶多项式。由此得到“惯容—弹簧”隔振器机械网络的阻抗表达式为

式中，a1、a3都是正的常系数，

这样，满足线谱和宽带一体化隔振技术条件的力传递函数综合转换为隔振器机械网络的阻抗函数综合。

3“惯容—弹簧—阻尼”隔振器结构综合

3.1 隔振器结构综合

在得到线谱和宽带一体化隔振器的机械网络阻抗函数的一般表达式后，可根据阻抗或其倒数导纳综合出隔振器的结构形式。由于阻抗综合的结构是并联网络，而导纳综合的结构是串联网络，按导纳综合，式（15）可展开成如下多项式

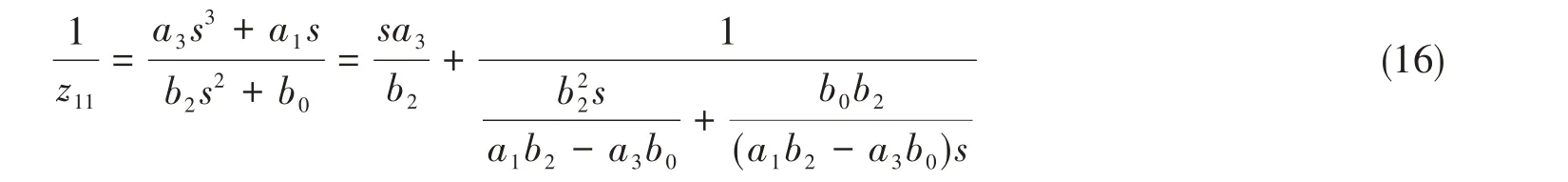
式中，最右端第1项是弹簧导纳，第2项是惯容和弹簧二元件并联导纳。

按阻抗综合，式（15）可展开成如下多项式

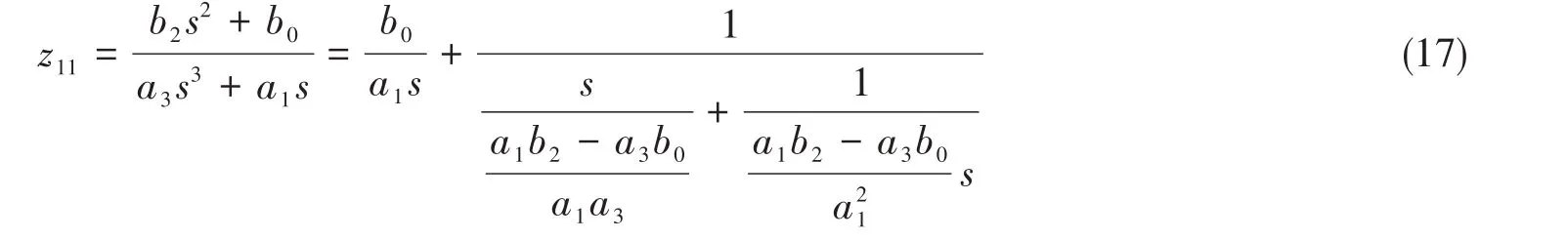
式中，最右端第1项是弹簧阻抗，第2项是惯容和弹簧二元件串联阻抗。

因此，满足线谱和宽带一体化隔振要求的隔振器结构应包括2个弹簧和1个惯容。由于惯容不具有独立承载能力，一旦超过工作行程将出现“击穿”短路，需要其中1个弹簧的并联防护。

按照上述两种综合方法构建的隔振器结构形式如图6 所示。结构Ⅰ是两级串联型，“惯容—弹簧”并联作为第一级，第2个弹簧作为第二级；结构Ⅱ是单级并联型，“惯容—弹簧”串联作为第一个并联分支，第2个弹簧作为第二个并联分支。

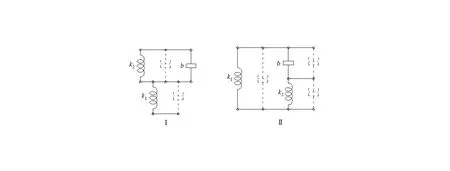
图6 隔振器结构形式Fig.6 Isolator structure

结构Ⅰ、Ⅱ的反共振频率分别为

在相同动力参数条件下，ωⅠ>ωⅡ。

为控制隔振系统的共振响应，在隔振器结构构成中还应设置阻尼，但阻尼元件数量是可选项。虽然阻尼的排列不影响力传递函数的性质，但有可能破坏反共振条件。根据前述“惯容—弹簧—阻尼”的匹配关系规律，阻尼应并联排列，如图6中的虚线位置。

3.2 隔振特性分析

设定阻尼元件数量不超过2 个，记为c1、c2，隔振器Ⅰ有3 种阻尼排列方式，分别记为Ⅰ1、Ⅰ2、Ⅰ3。隔振器Ⅱ有6种阻尼排列方式，分别记为Ⅱ1、Ⅱ2、Ⅱ3、Ⅱ4、Ⅱ5、Ⅱ6。

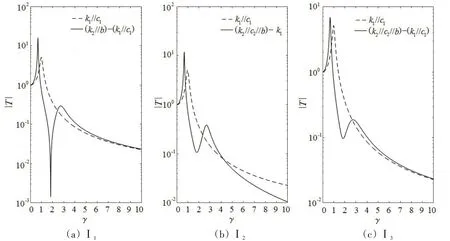
图7 隔振器Ⅰ的力传递函数幅频特性Fig.7 Amplitude-frequency characteristics of dimensionless force transfer function of Isolator Ⅰ

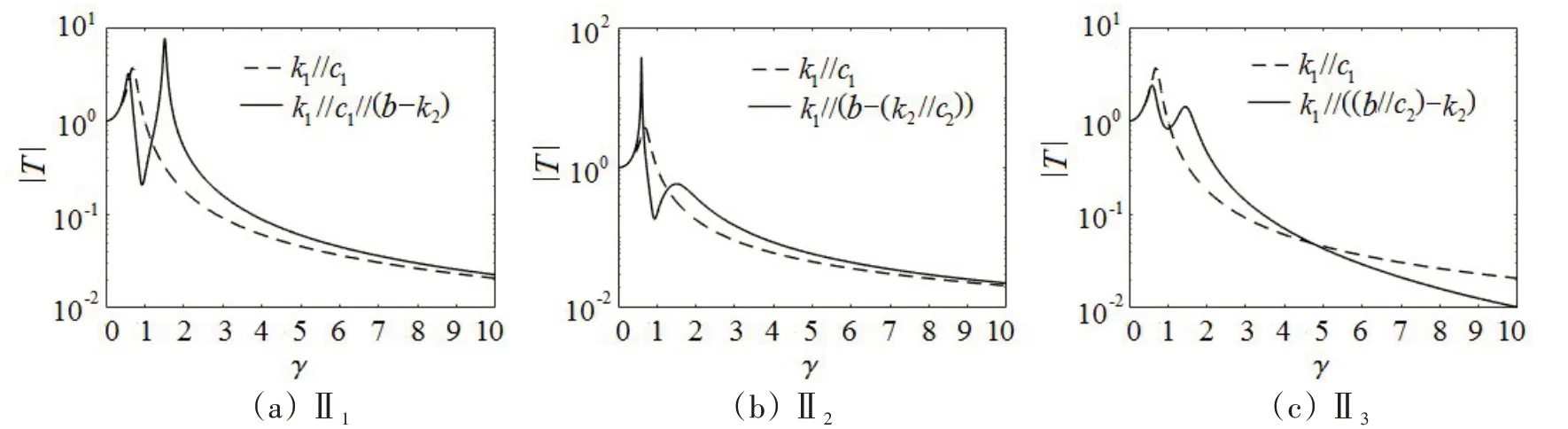
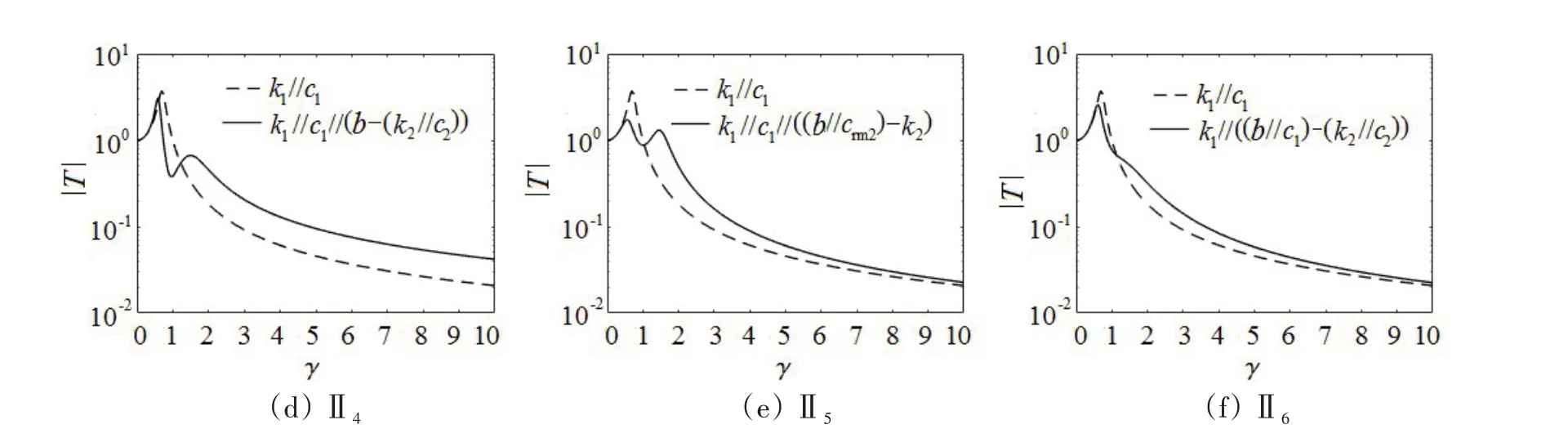
图8 隔振器Ⅱ的力传递函数幅频特性Fig.8 Amplitude-frequency characteristics of dimensionless force transfer function of Isolator Ⅱ

对比看出，基于“惯容—弹簧—阻尼”结构体系的隔振器Ⅰ、Ⅱ的力传递函数曲线都存在反共振峰，在隔振区的衰减斜率与传统隔振器也基本一致，证实了上述关于隔振器机械网络综合方法的正确性。

观察隔振器Ⅰ2和Ⅱ3，其力传递函数曲线在隔振区的衰减斜率较其他结构的力传递函数曲线更大，原因在于结构Ⅰ2和Ⅱ3力传递函数分母多项式与分子多项式的阶数差比其他结构力传递函数大1阶。在隔振区，结构Ⅰ2和Ⅱ3力传递函数曲线的下降速度为12 dB/Oct.，是其他结构的2 倍，达到双层隔振的衰减水平。

3.3 阻尼影响

阻尼的影响集中在共振区和反共振区，其作用是控制共振峰和反共振峰的幅值。通过比较力传递函数共振峰和反共振峰幅值的变化，可以识别不同位置阻尼的影响机制。

对于隔振器Ⅰ3，对比图7中Ⅰ1和Ⅰ3，可推知c2主要决定第1阶共振峰和反共振峰的幅值，并且对两者的影响作用相反，在降低第1 阶共振峰幅值的同时，也增大反共振峰的幅值，即削弱线谱隔振效果；由图7中Ⅰ2和Ⅰ3对比推知c1主要影响第2阶共振峰幅值。

阻尼c1和c2的影响作用和效果可以从图9进一步验证。在隔振区，增加阻尼c1会相应增大力传递函数幅值，不利于宽带隔振。而改变阻尼c2对宽带隔振效果几乎无影响，但会显著地影响线谱隔振效果。因此，隔振器Ⅰ的宽带隔振效果可通过调节阻尼c1改善，而线谱隔振效果由阻尼c2调节。

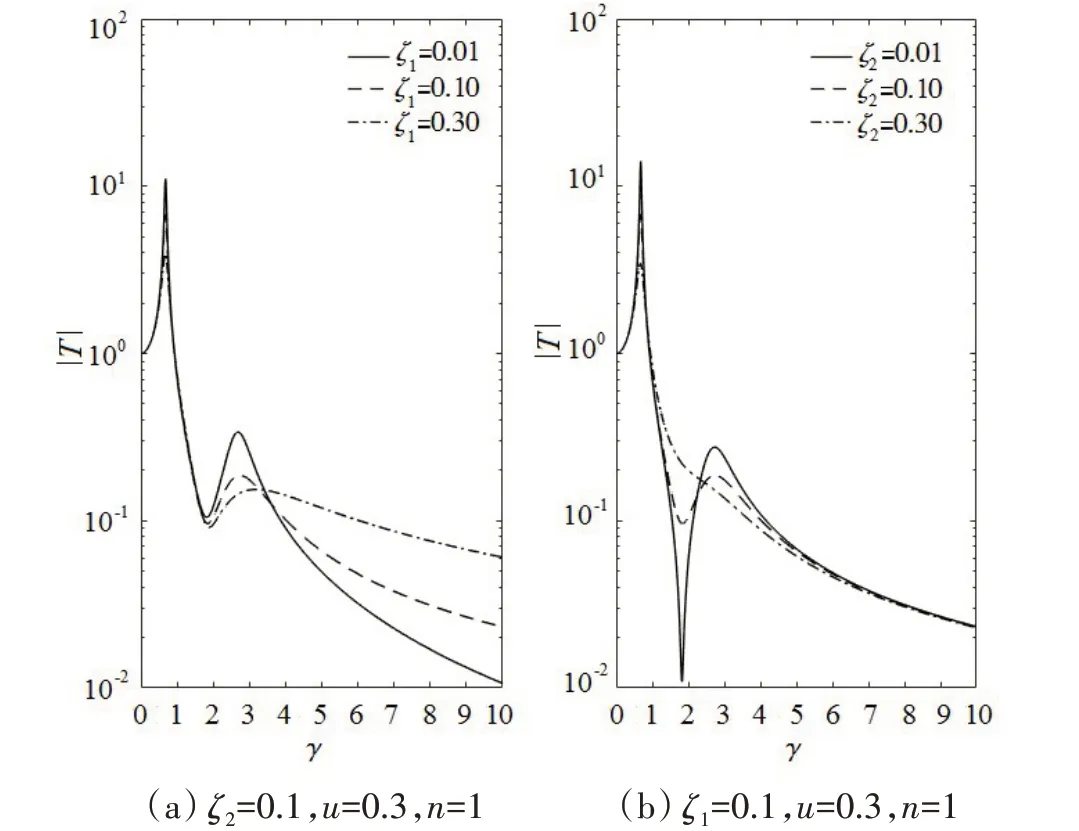
图9 隔振器Ⅰ3关于阻尼的影响Fig.9 Effect of damping on Isolator Ⅰ3

对于隔振器Ⅱ，由图8 中Ⅱ2和Ⅱ4、Ⅱ3和Ⅱ5对比，可推知c1决定第1 阶共振峰和反共振峰的幅值，并且对两者的影响作用也是相反的，第1个共振峰幅值被抑制的同时，会增大反共振峰幅值；由图8中Ⅱ1和Ⅱ4、Ⅱ5对比推知c2主要决定第2个共振峰幅值。

图10具体展示阻尼c1和c2对隔振器Ⅱ4的影响作用和效果。在隔振区，力传递函数幅值与阻尼c1和c2正相关，增加阻尼c1和c2都会降低宽带隔振效果。因此，阻尼c1同时决定了隔振器结构Ⅱ4的线谱和宽带隔振效果，而阻尼c2主要影响宽带隔振效果。

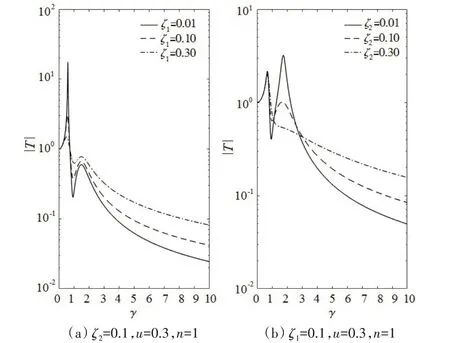
图10 隔振器Ⅱ4关于阻尼的影响Fig.10 Effect of damping on Isolator Ⅱ4

隔振器Ⅱ5关于阻尼的影响见图11。阻尼c1主要影响第1 阶共振峰幅值和宽带隔振效果，而第2阶共振峰幅值和线谱隔振效果由阻尼c2决定。因此，隔振器Ⅱ5的线谱和宽带隔振效果可以分别通过阻尼c1、c2进行独立调节，相对于隔振器Ⅱ4更有结构优势。

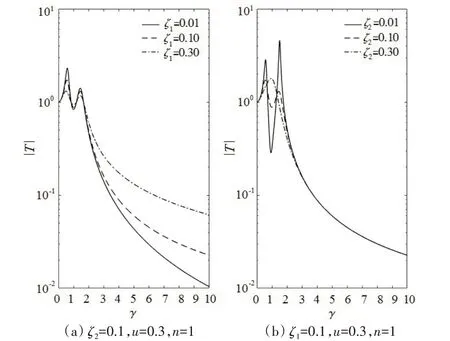
图11 隔振器Ⅱ5关于阻尼的影响Fig.11 Effect of damping on Isolator Ⅱ5

4 结 论

（1）在“惯容—弹簧—阻尼”三元件匹配关系中，惯容和弹簧并联形成反共振，在并联的惯容和弹簧结构中串联阻尼，将破坏反共振的条件，而在串联的惯容和弹簧结构中增加阻尼也不会出现反共振。

（2）线谱和宽带一体化隔振的技术条件反映在力传递函数表达式上时，分子多项式包含偶次的2阶多项式，通过反共振实现线谱隔振；分母多项式的阶数比分子多项式至少高1 阶，通过力传递函数幅值单调递减实现宽带隔振。

（3）存在两种类型的满足线谱和宽带一体化隔振技术条件的隔振器结构，分别是两级串联型和单级并联型；为实现线谱隔振效果和宽带隔振效果的独立调节，可以在两级串联型隔振器结构中与第一级和第二级各并联1个阻尼元件，或者在单级并联型隔振器结构中与分支和惯容各并联1个阻尼元件。