不同屈服准则对完好管道失效压力的影响分析

孙明明，李 昕

（1.郑州大学水利科学与工程学院，郑州 450001；2.大连理工大学a.海岸和近海工程国家重点实验室，b.工程抗震研究所，辽宁大连 116024）

0 引 言

钢管作为一种安全、经济的油气输送方式，在世界范围内得到广泛应用[1-2]。为了安全使用管道系统，有必要了解其所能承受的最大压力负荷。因此，准确预测其爆破压力是管道安全性和完整性评价中的重要考虑因素。内压失效压力通常被定义为在塑性失效时管道的极限载荷或失效压力。为了获得管道爆破压力的计算模型，专家学者进行了大量的理论、数值和实验研究，提出了无缺陷管道极限内压的解析公式或经验公式。

Cooper[3]和Svensson[4]通过使用von Mises 屈服准则和塑性失稳理论得到了柱形和球形容器失效压力的理论公式；Hiller[5]对承受内压和轴向载荷的薄壁管道进行了同类的理论失稳研究；Updike 等[6]基于同样的von Mises 准则，提出了预测拉伸塑性失稳中轴对称薄壁压力容器极限载荷的数学模型。由于von Mises 屈服准则表达式的非线性，使得基于该准则对结构进行弹塑性分析时得到的相关解表达式变得复杂。

针对完好管道失效压力，Zhu 等[7]应用Tresca 屈服准则得到了管道爆破压力。对于Tresca 屈服准则，由于其未考虑中间主应力的影响，对于部分材料是偏保守的，不能充分体现材料的潜在强度。Steward 等[8]分别基于Tresca 和von Mises 屈服准则，提出了两种无缺陷管道破裂压力理论解，发现不同延性钢的失效压力实验数据介于两种准则的预测之间：Tresca 屈服准则预测失效压力的下限和von Mises 屈服准则预测失效压力的上限。此外，Zhu 等[9]提出了平均剪应力屈服(ASSY)准则，用于对薄壁管道爆破压力的预测，证明了该准则的适用性。应力屈服准则[10]也被用于结构的弹塑性分析中，取得了较为满意的结果[11]。

Zhu等[9]和Law等[12]对薄壁管道的爆破压力公式进行了比较评述，Christopher等[13]对厚壁容器的爆破压力估算进行了比较研究，认为目前还没有一种准确和被广泛接受的评估方法。针对管道爆破失效压力的研究可知，不同屈服准则或者强度理论都有其自身的适用性，但是具体哪种屈服准则适合哪种属性材料尚无定论。Zhu等[14-15]认为：Tresca准则适用于高应变强化材料；von Mises准则适用于低应变强化材料；而两者的平均值可以用于预测中等应变强化材料的极限内压荷载。该结论没有给出具体管道属性与屈服准则的对应关系，因而在应用上有其局限性。统一屈服准则[16-18]是一种体现中间主应力效应以及能够适用于复杂应力状态的一种强度理论。统一屈服准则从一个统一的力学模型出发，得出一个统一形式的数学表达式，可以适用于不同属性的材料。该理论对工程结构进行极限分析具有优势，克服了单一屈服准则适用范围局限性的不足。本文基于该屈服准则的内压失效解析解，根据实际完好管道爆破试验，分析了不同材料属性管道内压失效时适应的屈服准则，并给出一种适用于多种钢材属性的无缺陷管道破裂压力的改进解析解。

1 爆破压力的解析解

1.1 简化与假设

为了推导完好管道极限内压荷载解析解，首先引入如下假设：（1）管道为薄壁结构；（2）管材在大塑性变形下，材料不可压缩；（3）对于长管道，忽略内压作用下其轴向应变[19-20]；（4）基于Hill 的塑性功假设和薄壁管道的应力和应变状态[9,21]。

海底管道在内压荷载作用下，随着内压的逐渐增加，管道的横截面逐渐扩展，壁厚逐渐减少。管道外壁首先达到屈服，并逐渐沿着管壁厚度扩展，当内压荷载达到特定值时，管壁厚度方向全部达到屈服，当管材的应变强化效应不再能补偿内压荷载引起的管壁减薄时，从而引起管道局部的膨胀和破裂，管道发生失效破坏，此时对应的内压荷载为管道的极限内压荷载，也就是爆破内压或失效内压管线在接近塑性倒塌破坏时，通常会发生较大的塑性变形。在这种情况下，考虑用应变强化效应来描述钢管的应力应变响应。

1.2 统一屈服准则

统一屈服准则[16-18]规定当两个较大主剪应力的某个函数达到极限值时，材料就会失效。该理论包括了第二主应力σ2对材料强度的贡献，并采用统一的力学模型描述了材料的塑性特征。对于钢质管道可看做拉压同性材料，统一屈服准则的数学表达式如下：

式中，τ13、τ12和τ23分别为主剪应力。如果σ1、σ2和σ3是主应力，并且σ1≥σ2≥σ3，则τ13=(σ1-σ3)/2，τ12=(σ1-σ2)/2，τ23=(σ2-σ3)/2。C为材料强度参数，可以表达为

式中，σUE为统一屈服准则的等效应力。将式（2）代入式（1）可得

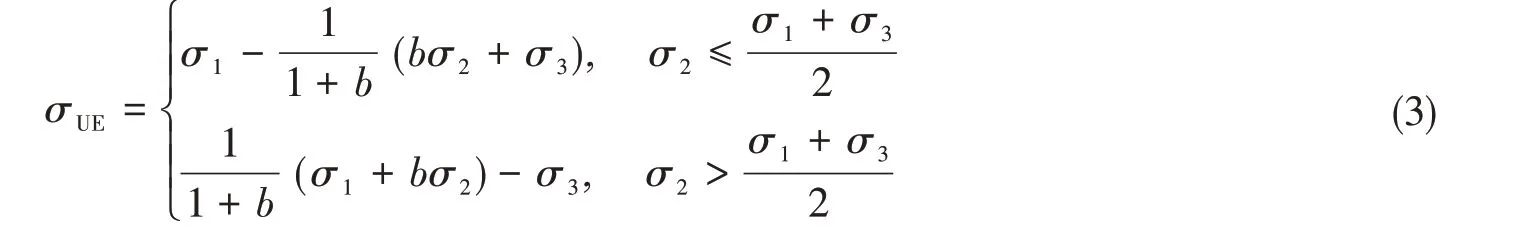
参数b是反映中间主剪应力影响的权系数。从统一屈服准则中可以看出参数b具有重要的作用，它反映了中间主剪应力对材料塑性失效的影响程度。另一方面，它也把不同的屈服准则有区分地联系了起来。对于不同的b值，统一屈服准则代表或接近所有通用的屈服准则。因此，统一屈服准则不能被认为是一个简单的屈服准则，而是一个包含一系列屈服准则的理论体系，它可以适用于各种不同的材料。

1.3 爆破压力推导

在内压荷载作用下，管道失效之前往往要经历大的塑性变形，研究表明采用幂次强化模型可以很好考虑应变强化效应，幂次强化模型可以表示为

式中，K为强化系数，n为强化指数，σ′为真实应力，ε′为真实应变。

管道是薄壁结构，由平衡方程可知：

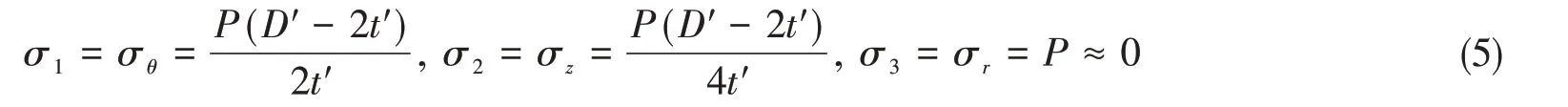
式中，D′为管道在内压荷载作用下发生变形后的外直径，t′为发生变形后的管道厚度。该平衡方程在弹性阶段和塑性阶段都成立，同时适用于小应变理论和有限应变理论。在管道发生大的塑性变形时，管材可近似认为不可压缩，εθ+εr+εz= 0，轴向应变很小可以忽略不计，εz≈0[19-20]，因此εθ= -εr.根据有限应变理论，管道的应变可以表示为

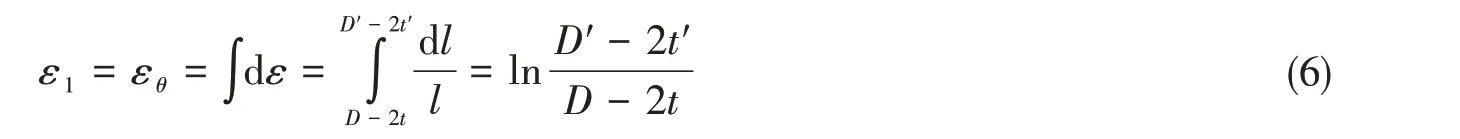
同理，

式中，D为管道发生变形前的外直径，t为发生变形前的管道厚度。

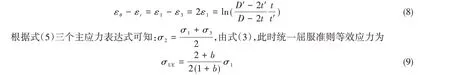
基于Hill的塑性功假设和薄壁管道的应力和应变状态[3,20]，

式中，εUE表示统一屈服准则等效应力对应的等效应变。将式（8）和式（9）代入式（10），得

根据式（8）可以得到：

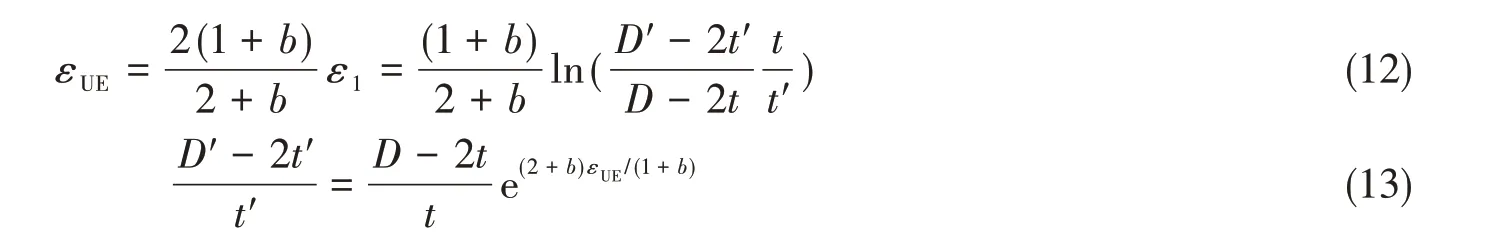
根据式（4）、式（5）、式（9）和式（13），管道内压可以表示为

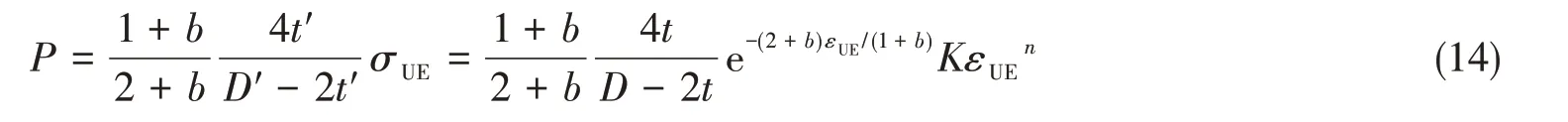
当爆破失效压力P取到极值时，对式（14）等效应变εUE求导数为0，即

根据工程极限抗拉强度σu，强化系数K可以表示为[8]

将式（15）和式（16）代入式（14），可以得到不同屈服准则的完好管道的极限内压荷载：

1.4 解析解讨论

必须指出，以上基于对管线进行塑性破坏分析的统一屈服准则的失效压力预测方法克服了单一屈服准则针对一种或几种特殊材料的局限性。统一屈服准则是反映中间主应力效应的强度理论，适用于复杂的应力状态，同时也适用于不同性质的材料。该理论在工程结构极限分析中具有优势，克服了单一屈服准则的局限性[22]。由式（17）可知，管道失效压力受参数b、强化指数n、壁厚t、直径D和抗拉强度σu影响。其中参数b决定了中间主剪应力对爆破压力和屈服准则的影响，该参数不同取值可以得到不同屈服准则下封闭管道爆破压力解：

（1）当b=0 时，管道失效等效应力仅由第一主剪应力决定，这个由式（17）给出的解析解为Tresca屈服准则的失效压力解：

（2）当b=(8 3 - 10)/23 ≈0.168 时，管道失效等效应力主要由第一主剪应力决定，式（17）解析解为基于平均剪应力屈服准则（ASSY）的失效压力解:

（3）当b=1/（1+ 3）≈0.366 时，管道失效等效应力主要由第一主剪应力决定，式（17）解析解为基于von Mises 准则的失效压力解：

（4）当b=1 时，管道失效等效应力由第一主剪应力和第二主剪应力共同决定，两者权重一致，式（17）解析解为基于双剪应力屈服准则（TSSY）的失效压力解：

2 管道内压失效强度差异与失效压力计算

Zhu和Leis[7,9,14-15]指出，不同材料属性的钢制管道适应的屈服准则并不相同，而且爆破压力的预测和屈服准则的选择主要随材料的屈强比和强化指数n的变化而变化。因为统一屈服准则（UYC）不是一个简单的强度准则，而是一个包含一系列强度准则的理论体系。它可以适用于各种不同的材料，该屈服准则克服了单一屈服准则的局限性，因此采用该模型进行管道内压失效屈服准则差异性分析。由1.3节分析讨论可知，管道屈服准则的选择主要由参数b决定。

2.1 管道在内压作用下参数b的确定

为了得到不同材料属性钢制管道内压失效适应的屈服准则，决定选取实际完好管道内压失效实验数据进行分析。令完好管道实际爆破压力P0和基于统一屈服准则的管道失效压力解析解式（17）相等：

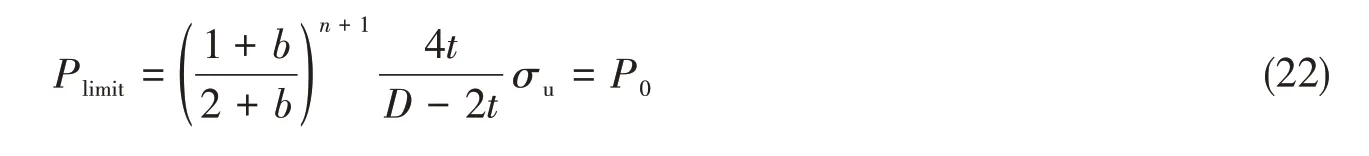
则有

管道的应力应变真实值和工程值的关系可以表示为

式中，ε′为真实应变，ε为工程应变，σ′为真实应力，σ为工程应力。

强化指数n和应变的关系可以表示为[14-15]

式中，εu和ε'u分别是极限拉应变工程值和真实值，

由式（4）、式（24）和式（25）可以得到强化指数与屈服强度和极限抗拉强度的函数关系：

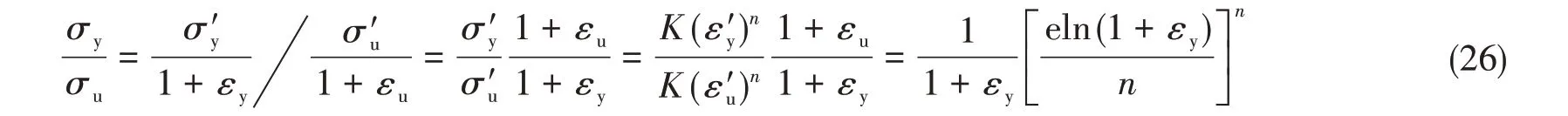
通常将对应于塑性应变为0.2%时的应力定义为屈服强度，此时屈服应变εy= 0.002 +σy/E，E为管道弹性模量。

式（26）表明，管材的屈强比是应变强化指数和屈服应变εy的函数。在已知管材的屈服强度和抗拉强度的情况下，可求解得到管材的强化指数。

本文搜集了55个管道全尺寸爆破试验，Mok等[23]做了两例关于X60的完好管道破坏实验；Liessem等[24]做了7 例关于X60、X65、X70 和X80 的完好管道破坏实验；Hillenbrand 等[25]做了两例关于X100 的完好管道破坏实验；Okaguchi 等[26]做了两例关于X80 和X120 的完好管道破坏实验；Papka 等[27]做了9例关于X120完好管道破坏实验；Paslay 等[28]做了14例从K50-Q125的完好管道破坏实验；Netto 等[29]做了1 例关于AISI 1020 完好管道破坏实验；Freire 等[30]做了1 例关于X80 完好管道破坏实验；Benjamin等[31]做了1 例关于X80 完好管道破坏实验；帅健[32]搜集了8 例关于X46 和X52 的完好管道破坏实验；Cronin 等[33]做了8 例关于X46 和X52 完好管道破坏实验。完好管道爆破实验钢材强度从AISI 1020 到X120，实验涵盖了低、中和高三种等级强度钢材。具体实验数据如表1所示。

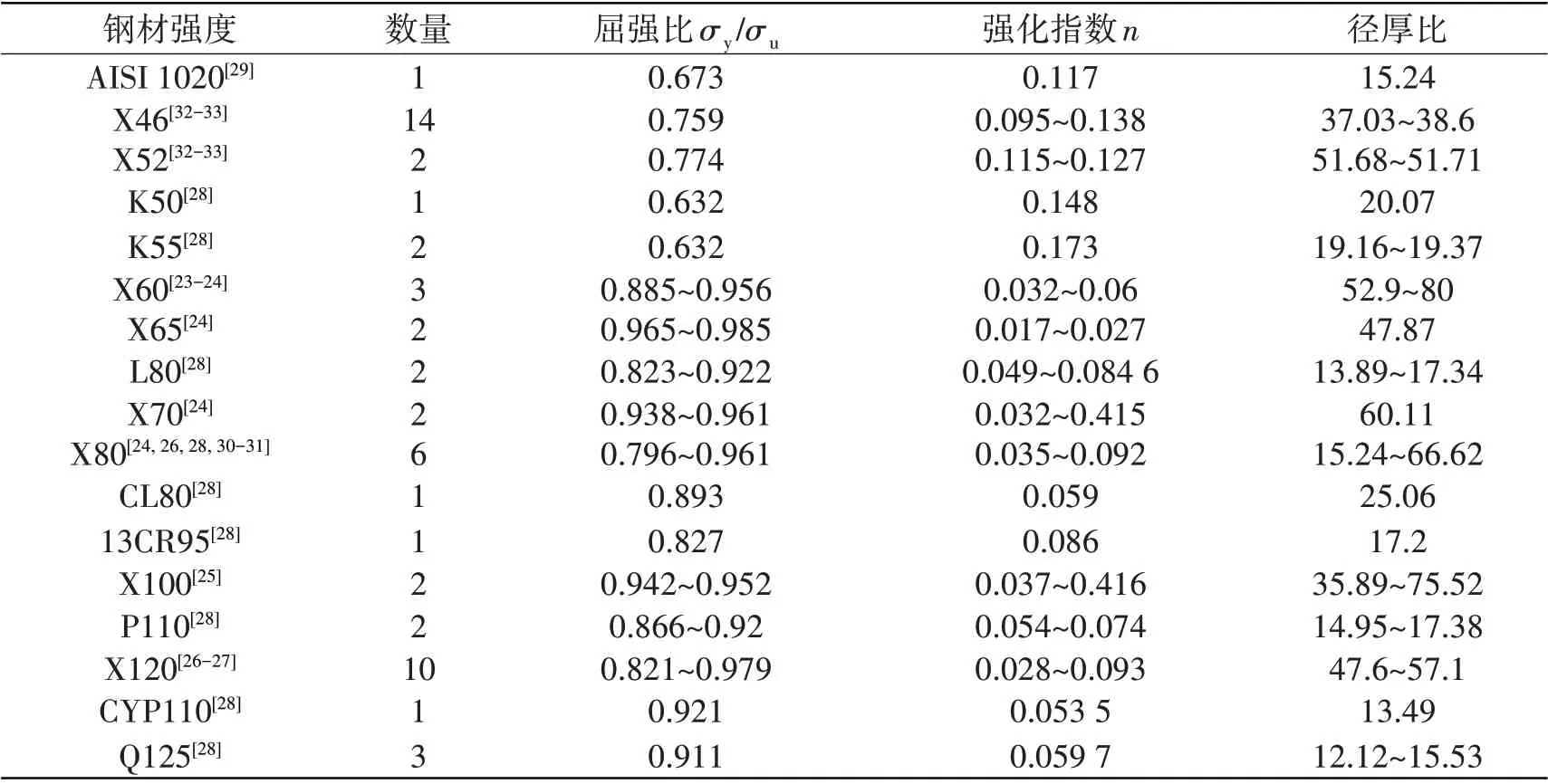
表1 实验数据Tab.1 Test data

图1为55个完好管道爆破试验中，由爆破压力计算得到的参数b与相应的强化指数n关系图。强化指数n从0.06～0.18 基本涵盖了强化指数n所有数值[14-15]。由图1 中看出，von Mises 屈服准则结果是钢制管道内压失效的上限，Tresca屈服准则结果是内压失效下限，TSSY失效准则不适用于钢制管道内压失效破坏准则。

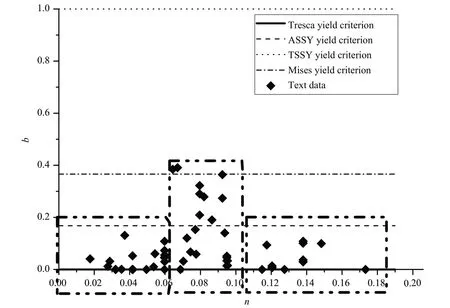
图1 完好管道强化指数与屈服准则Fig.1 n and yield criteria of defect-free pipeline

考虑到晶体结构和生产工艺的差异性，即使同一种强化指数的材料，其内压失效时所适合的屈服准则也并不相同，当0.06 ≤n< 0.11时，这种差异性最为明显。管道失效时屈服准则的不同，失效压力计算结果也并不相同，当管道强度指数n在（0，0.18）范围内时，管道屈服准则适用范围为在von Mises屈服准则和Tresca 屈服准则之间。在进行管道爆破压力预测时，运用von Mises 准则得到的是爆破压力的上限，Tresca准则得到的是爆破压力下限。

由图1看出，完好管道的屈服准则主要分为三部分：

（1）当0 ≤n< 0.06时，根据完好管道爆破试验确定的参数b分布在0和0.168之间，该类型管材运用ASSY准则得到的是爆破压力的上限，Tresca准则得到的是爆破压力下限；

（2）当0.06 ≤n< 0.11 时，完好管道爆破试验确定的参数b分布在0 和0.366 之间，该类型管材运用von Mises准则得到的是爆破压力的上限，Tresca准则得到的是爆破压力下限；

（3）当0.11 ≤n< 0.18时，完好管道爆破试验确定的参数b分布在0和0.168之间，该类型管材运用ASSY准则得到的是爆破压力的上限，Tresca准则得到的是爆破压力下限。

2.2 改进管道失效压力计算

图2为参数b随着强化指数n的变化趋势图，虚线为变化趋势线。

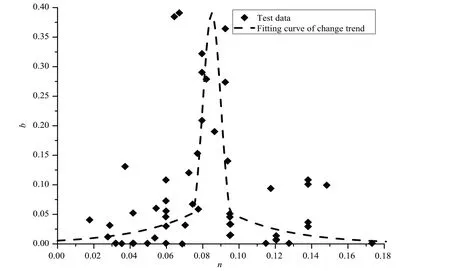
图2 参数b变化趋势图Fig.2 Variation of b with n

由图中可以看出，完好管道的爆破试验数据大致呈“钟形”分布，两边低，中间高。实验数据点大致关于n= 0.085 对称，当n→0 和n→0.18 时，b值趋向于0。根据参数b变化规律，考虑采用下列方式进行参数b的拟合：

（1）参数b以n= 0.085呈轴对称分布；

（2）0 ≤n< 0.075和0.095 ≤n< 0.18范围内参数b采用指数函数进行拟合；

（3）0.075 ≤n≤0.095范围内参数b采用凸函数拟合，因为参数b最大值为0.391，该函数最大值为0.391；

（4）分段函数在n= 0.075和n= 0.095两个节点数值相等。

根据参数b随着强化指数n的变化趋势，拟合函数如下：

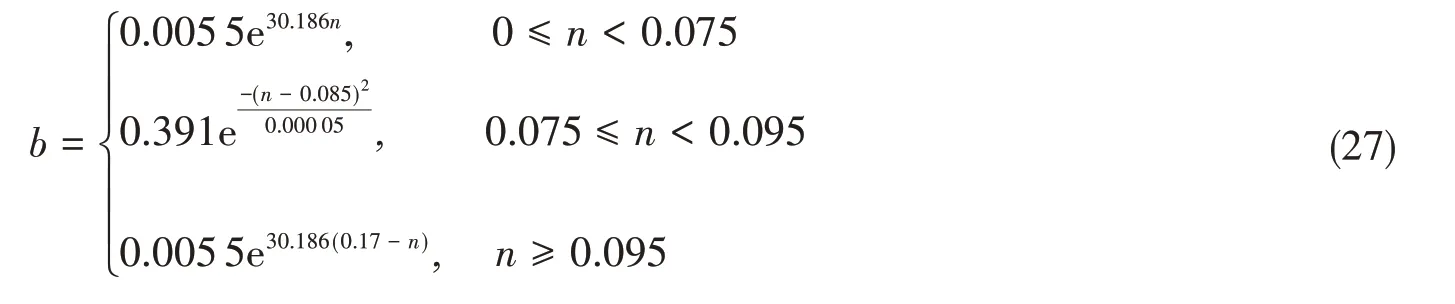
2.3 改进计算方法验证

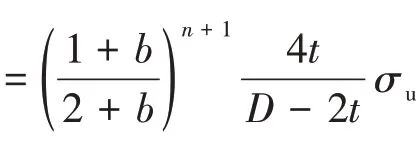
表2 不同计算方法误差绝对值比较Tab.2 Comparison of the errors of different calculation methods

由表2中可以看出，统一屈服准则计算方法平均误差最小为4.3%，将完好管道失效压力平均误差控制在5%以内。其它方法误差从小到大依次为：Tresca 屈服准则、ASSY 屈服准则和von Mises 准则。统一屈服准则计算方法最大误差为14%，是所有计算方法中最小值，误差最小值为0.157%，仅低于von Mises屈服准则。

表3为不同误差区间频率分布，表中数据为误差范围内的实例数量与总数的比值。由表3中可以看出，改进统一屈服准则实例验证中有36.36%的误差控制在2%以内，超过现有评价方法最大值（Tr⁃esca 准则）的两倍；41.82%的误差控制在3%以内，65.45%的误差控制在5%以内，92.73%的误差控制在10%以内，均大于其它屈服准则计算方法。本章得到的基于统一屈服准则的改进完好管道失效压力计算方法用于完好管道评估时，可以得到更准确的预测值。

表3 不同计算方法误差区间分布Tab.3 Error distributions for the different methods

3 结 论

本文对不同材料属性的管道内压失效时适应的屈服准则进行了分析，得到如下结论：

（1）不同材料属性的管道所适用的屈服准则并不相同，它随着管材强化指数、屈强比、屈服强度和抗拉强度等的变化而变化。管道爆破失效压力预测中，Mises准则是压力预测的上限，Tresca准则是压力预测的下限，力屈服准则不适用于管道内压破坏失效压力评估。

（2）不同强化指数n下参数b的分布类似于“钟形”分布，实验数据点大致关于n= 0.085对称。当0 ≤n< 0.06 和0.11 ≤n< 0.18 时该类管道材料运用ASSY 准则得到的是爆破压力的上限，Tresca 准则得到的是爆破压力下限；当0.06 ≤n< 0.11时，该类管道材料运用von Mises 准则得到的是爆破压力的上限，Tresca准则得到的是爆破压力下限。

（3）针对完好管道的失效压力评估，常规三种屈服准则中适用性最好的是Tresca 屈服准则，其次是ASSY 屈服准则和von Mises 准则。本文基于统一屈服准则，提出了一种新的完好管道失效压力评价方法，相比常规三种屈服准则评价方法，该方法的预测结果与实验结果吻合更好，误差更小。