砂土地基中刚性单桩水平极限承载力改进计算方法

付臣志，江杰，欧孝夺，龙逸航，张探

（1.广西大学土木建筑工程学院，广西南宁，530004；2.广西大学工程防灾与结构安全教育部重点实验室，广西南宁，530004；3.广西大学广西防灾减灾与工程安全重点实验室，广西南宁，530004）

海上风力涡轮机通常采用超大直径刚性单桩作为基础，它会承受由上部结构传递的水平力和弯矩作用，其安全性和稳定性成为保障风力涡轮机安全运行的关键[1]。水平荷载作用下刚性单桩的设计准则之一是计算其极限承载力，目前的极限承载力计算模型大多基于试验结果提出[2-4]，对刚性桩的桩-土相互作用问题认识还不够深入，而桩-土相互作用问题是桩基水平承载性能研究中必须考虑的重要内容，该问题的研究对于完善桩基础设计理论和指导工程实践具有重要意义[5]。

大量学者对砂土地基中刚性单桩的水平极限承载力计算模型进行了研究，BRINCH[2]、BROMS[3]、PETRASOVITS 等[4]和MEYERHOF 等[6]分别提出了不同的计算模型，如图1所示。图1中：e为荷载作用点高度；a为旋转点深度；L为桩长；Pu为极限土抗力；Hu为极限承载力。上述模型均假定桩侧土抗力沿桩周均匀分布，随着研究的深入，PRASAD等[7]发现桩侧径向土压力并非沿桩周均匀分布，而是由桩周中心处向两端逐渐减小。同时，PRASAD等[7]还测得了极限状态下土抗力沿深度的分布形式，建立了新的水平极限承载力计算模型，但该模型忽略了环向摩阻力的影响。对此，ZHANG 等[8]基于SMITH[9]和BRIAUD 等[10]提出的环向摩阻力沿桩周的分布形式，建立了同时考虑径向土压力和环向摩阻力的水平极限承载力计算模型。虽然该模型克服了不能考虑环向摩阻力的缺点，但仍存在不合理之处。YANG等[11]通过数值模拟方法对水平受荷刚性桩的桩-土相互作用进行了研究，结果表明极限状态下ZHANG 等[8]考虑的环向摩阻力分布与实际分布差别较大，因此，需要一种准确考虑环向摩阻力的极限土抗力计算方法。此外，YANG等[11]还指出当刚性单桩绕旋转点发生刚体转动时，桩端土体对桩端运动的阻碍作用使得桩端存在水平力和弯矩作用，桩身与桩侧土体的竖向相对滑动产生的竖向摩阻力对桩身旋转起到抵抗力矩作用，称之为侧阻抗力矩[12]，而现有水平极限承载力计算模型均未考虑这两者的有利作用，使得计算的水平极限承载力偏小，因此，一种考虑侧阻抗力矩、桩端水平力和弯矩影响的刚性桩水平极限承载力计算模型亟待提出。另外，若考虑侧阻抗力矩作用，则桩侧同时存在竖向摩阻力与环向摩阻力，而目前关于同时考虑竖向摩阻力和环向摩阻力的土抗力和侧阻抗力矩计算方法也未见报道。

图1 极限承载力计算模型Fig.1 Calculation models of lateral ultimate bearing capacity

鉴于此，本文作者从桩-土相互作用出发，基于实际径向土压力分布，并考虑环向摩阻力和竖向摩阻力的共同作用，分别对极限土抗力和侧阻抗力矩进行推导，在此基础上，建立考虑侧阻抗力矩、桩端水平力和弯矩影响的刚性单桩水平极限承载力计算模型，并给出其解析解。通过算例分析对极限土抗力、侧阻抗力矩以及水平极限承载力改进计算方法进行验证，并通过参数分析探讨水平极限承载力的变化规律。

1 水平极限承载力问题描述与基本假定

1.1 问题描述

刚性单桩受荷载变形示意图如图2所示。从图2可见：当桩顶受到水平荷载H（作用点到地面距离为e）作用时，刚性单桩整体会围绕着旋转点（z=a）发生刚体转动，且没有明显的材料变形。桩身材料以及截面通常可以满足承载力要求而不发生破坏，桩-土体系的破坏只会发生在桩周土体中。随着桩身水平位移增加，浅层土体出现塑性变形并向深层土体逐渐发展，直到土体整体失稳破坏，最终导致桩-土体系的破坏。因此，研究刚性单桩的水平极限承载力问题，实际上是分析极限状态下桩周及桩端土体对刚性单桩的作用力问题，即桩-土相互作用问题。基于已有研究成果，水平受荷刚性单桩的桩-土相互作用问题可分为以下4 个方面：桩侧土抗力P、桩身侧阻抗力矩Ms、桩端水平力Hbu和弯矩Mbu。综合考虑这4个方面，并带入水平承载力计算模型进行求解，即得刚性单桩的水平极限承载力。

图2 刚性单桩受荷变形示意图Fig.2 Deformation diagram of rigid pile under lateral load

水平受荷桩桩-土相互作用可分为2 个区域：桩移动方向前方，土压力增大，称为被动侧；桩移动方向后方，土压力减小，称为主动侧。在极限状态下，只考虑被动侧桩周土体的抗力作用，该抗力作用由径向土压力和环向摩阻力2个部分组成，因此，求解极限土抗力的关键是确定径向土压力和环向摩阻力的分布形式。SMITH[9]和BRIAUD等[10]给出了径向土压力水平分量和环向摩阻力水平分量沿桩周的分布形式，如图3所示。

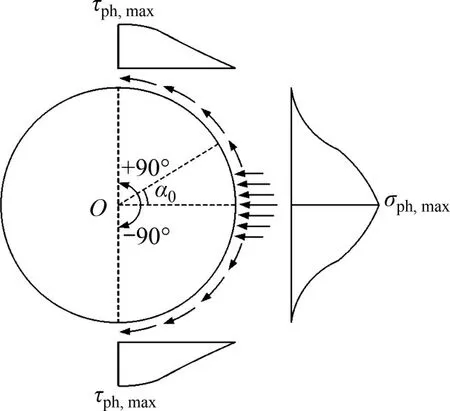
图3 被动侧桩周土抗力分布Fig.3 Distribution of soil resistance on passive side of pile

基于该分布模式，ZHANG 等[8]提出了考虑环向摩阻力影响的极限土抗力计算公式：

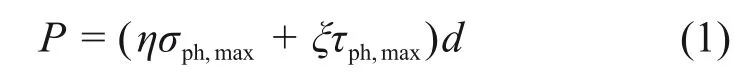
式中：σph,max为被动侧α0=0°处径向土压力极限值；τph,max为被动侧α0=±90°处环向摩阻力水平分量极限值；η为描述桩侧径向土压力水平分量不均匀分布的形状系数，对于圆形截面桩，η=0.8，对于矩形截面桩，η=1.0；ξ为描述桩侧径向土压力水平分量不均匀分布的形状系数，对于圆形截面桩，ξ=1.0，对于矩形截面桩，ξ=2.0；d为桩径。

从YANG 等[11]的研究结果可知，ZHANG 等[8]采用的桩侧土抗力的分布形式与实际形式差别较大。极限状态下桩侧土抗力如图4所示。由图4和图3可知：在极限状态下，径向土压力水平分量沿桩周的分布形式大致相同，但环向摩阻力水平分量沿桩周的分布形式差异明显，表现为环向摩阻力水平分量最大值由α0=±90°向α0=0°方向移动，这表明图3中的环向摩阻力水平分量并不符合实际受力状态。当环向摩阻力水平分量最大值由α0=±90°向α0=0°方向移动时，径向土压力逐渐增大使得环向极限摩阻力增大，从而导致按式（1）计算的环向摩阻力水平分量最大值τph,max偏小，低估了环向摩阻力水平分量对土抗力的贡献。

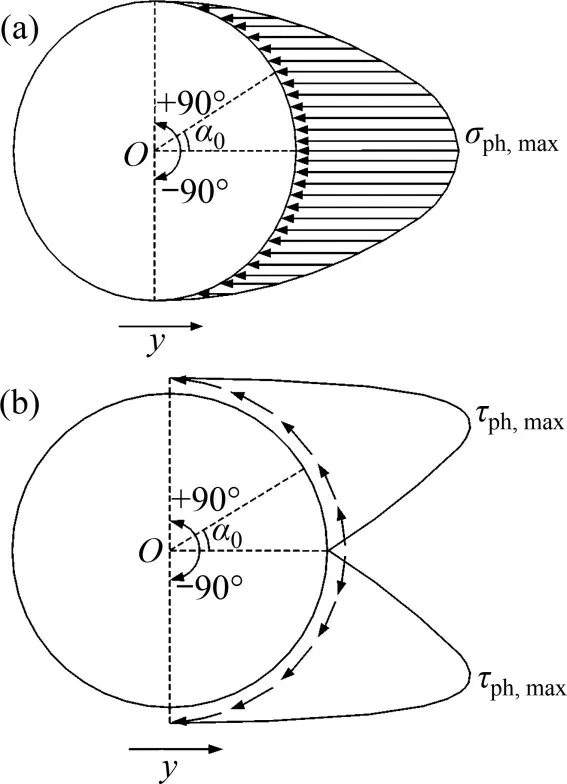
图4 极限状态下桩侧土抗力Fig.4 Distribution of horizontal component of soil resistance around pile in the limit state

为了便于分析，竺明星等[12]假定被动侧桩周径向土压力为均匀分布（为P/d），求解了桩身侧阻抗力矩，这使得桩周中心的竖向摩阻力偏小，桩周边缘的竖向摩阻力偏大，从而导致桩周中心的侧阻抗力矩偏小，桩周边缘的侧阻抗力矩偏大。此外，土抗力P包含了径向土压力水平分量和环向摩阻力水平分量，以P/d作为径向土压力也偏离了实际。因此需得到更符合实际的径向土压力，从而解决这2 个因素的影响，以求得更准确的侧阻抗力矩。

由前面分析可知，水平受荷刚性单桩极限承载力理论分析方法主要存在以下4个问题：1）现有极限土抗力计算方法无法更准确地考虑环向摩阻力的影响，这使得计算的极限土抗力不够准确；2）传统水平极限承载力计算模型均未考虑侧阻抗力矩、桩端水平力和弯矩的影响，这会显著低估刚性桩的水平极限承载力；3）当前侧阻抗力矩计算方法未能准确考虑径向土压力的实际分布形式，使得桩周中心的侧阻抗力矩偏小，桩周边缘的侧阻抗力矩偏大；4）由于桩身同时存在竖向摩阻力和环向摩阻力，因此，需要考虑两者的相互影响，否则会高估竖向摩阻力和环向摩阻力，从而导致极限土抗力P和侧阻抗力矩Ms偏大。

1.2 基本假定

在极限状态下，土抗力与侧阻抗力矩均分布于桩身被动侧，以旋转点为临界点，旋转点上下桩侧竖向摩阻力与环向摩阻力分布如图5（a）所示。鉴于目前尚无文献报道，同时考虑桩身竖向和环向摩阻力的水平承载力分析方法，本文对极限状态下两者的关系进行假设。

假设极限状态下桩侧竖向摩阻力τv与环向摩阻力τt相等，但两者均小于极限摩阻力τf[13-14]，如图5（b）所示。根据τv与τt合力等于τf，可建立如下关系式：

图5 竖向与环向摩阻力共同作用示意图Fig.5 Schematic diagram of coupling action of vertical and circular friction resistance

式中：τf为极限摩阻力，其表达式如下：

式中：μ为桩土摩擦因数，μ=tanδ，δ为桩-土界面摩擦角；σpr,i为径向土压力。对于比较光滑的桩，取δ=（0.5～0.7）φ′，对于比较粗糙的桩，取δ=（0.7～0.9）φ′，φ′为土体的有效内摩擦角[15]。

本文综合考虑上述4个问题，在合理的假设基础上，通过求解被动侧桩周的实际径向土压力，得到实际的环向摩阻力和竖向摩阻力，从而给出更准确的极限土抗力和侧阻抗力矩，最终得到改进的刚性单桩水平极限承载力解答。与已有文献结果相比，本文方法计算精度更高。

2 改进计算方法

2.1 实际径向土压力求解

当桩身水平位移为零时，桩周土压力均为静止土压力；当桩身发生水平位移时，被动侧桩对土体的挤压作用使得桩周径向土压力逐渐增大到被动极限土压力，因此，极限状态下被动侧桩周径向土压力可视为由初始径向土压力σ0和径向土压力增量Δσpr,i2个部分组成，如图6所示（其中：y为桩身水平位移）。初始径向土压力即为静止土压力，其表达式为

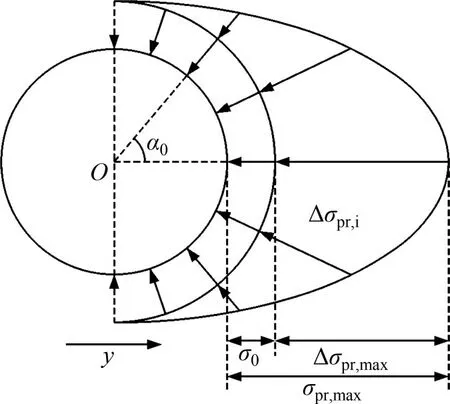
图6 桩周径向土压力分布Fig.6 Distribution of radial soil pressure around pile

式中：K0为静止土压力系数，K0=1-sinφ′；γ为土的重度。

将由水平荷载引起的径向土压力视为径向土压力增量，通过PRASAD等[7]的拟合结果可以得到被动侧桩周的径向土压力增量Δσpr,i：

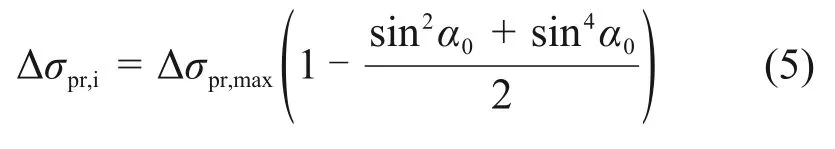
式中：Δσpr,i为被动侧桩周的径向土压力增量；Δσpr,max为被动侧α0=0°处的径向土压力增量。在极限状态下，Δσpr,max=σpr,max-σ0，其中，σph,max为α0=0°处的径向土压力极限值。根据ZHANG 等[8]离心模型试验结果可取σph,max=Kp2γz（其中，Kp为被动土压力系数，Kp=tan2（45°+φ/2），φ为土的内摩擦角）。

在式（5）的基础上，考虑初始径向土压力σ0，可得被动侧桩周实际径向土压力σpr,i：

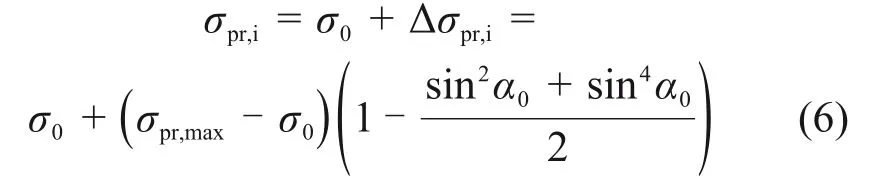
2.2 极限土抗力求解

求解桩周实际径向土压力分布后，可分别解得由径向土压力和环向摩阻力提供的土抗力。取单位桩长进行分析，被动侧桩周的径向土压力水平分量σph,i为

通过积分可以得到单位桩长由径向土压力提供的土抗力P1：

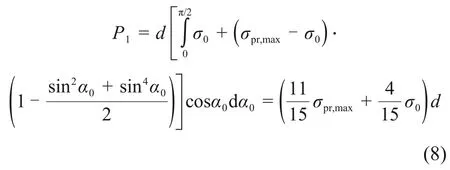
由图4（b）可知：桩周环向摩阻力水平分量由α0=0°向α0=±90°先增大后减小。本文考虑实际径向土压力分布，根据式（6）求得被动侧桩周环向极限摩阻力水平分量ft,p为

在此基础上，通过积分可得单位桩长由环向摩阻力提供的土抗力：

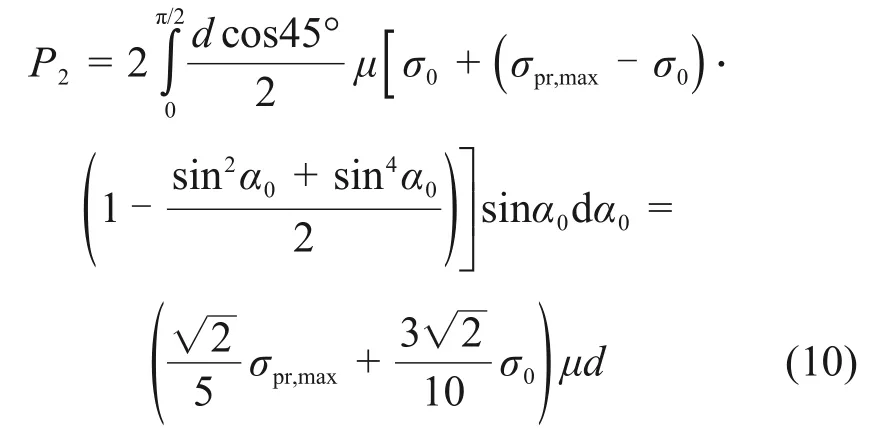
综合式（8）和式（10）可得根据实际径向土压力分布，考虑竖向摩阻力和环向摩阻力共同作用的刚性桩任意深度处的极限土抗力P：

2.3 极限状态下侧阻抗力矩求解

当刚性桩绕旋转点发生整体旋转时，桩身与桩侧土体会产生竖向剪切作用，由此产生的竖向摩阻力会对桩横截面中心产生力矩作用，从而减小桩身水平位移。竺明星等[12]假定被动侧桩周的径向土压力均等于土抗力P与桩径d的比值，实际上，被动侧桩周的径向土压力由α0=0°向α0=±90°逐渐减小。基于此，本文考虑桩周实际径向土压力分布对侧阻抗力矩进行求解，取任意深度处桩横截面微段进行分析，如图7所示，第i段圆弧中心点到轴线AC的距离为

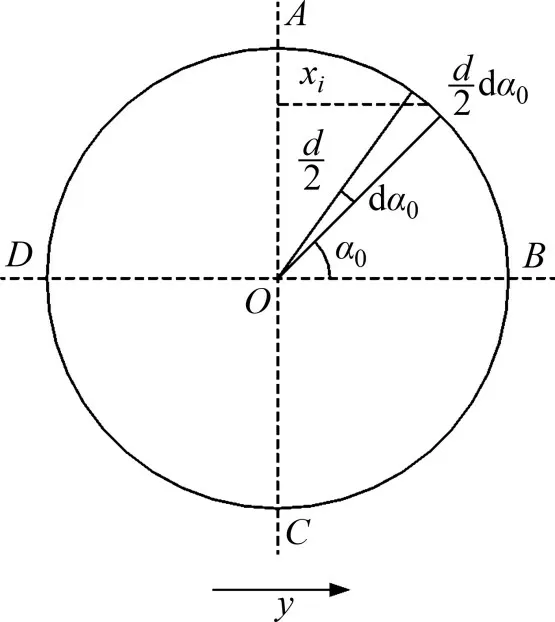
图7 侧阻抗力矩计算模型Fig.7 Calculation model of shaft resisting moment around pile

考虑竖向摩阻力与环向摩阻力的共同作用，可得第i段圆弧的竖向摩阻力：

由该竖向摩阻力产生的竖向力为

通过积分可得圆弧AB和BC的竖向力对单位长度桩身截面AC轴产生的抗力矩之和：

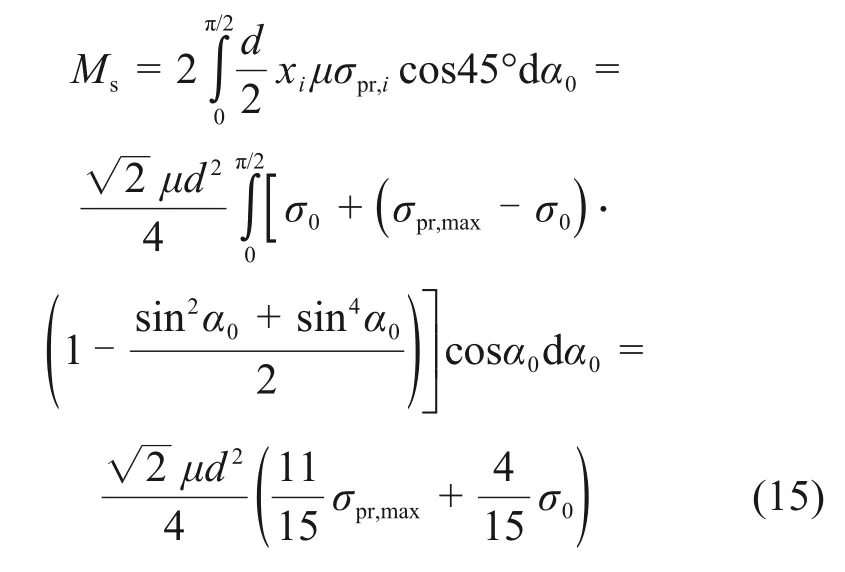
2.4 水平极限承载力求解

当前水平受荷刚性单桩极限承载力计算模型仅考虑了桩侧土抗力，本文进一步考虑侧阻抗力矩、桩端水平力和弯矩的影响，建立图8所示的水平极限承载力计算模型。以旋转点为临界点，旋转点以上，极限土抗力和侧阻抗力矩随深度线性增加。当深度达到0.6a时，极限土抗力和侧阻抗力矩达到最大，分别记为F和Ms。由于旋转点处水平位移为零，因此，随着深度进一步增大，极限土抗力和侧阻抗力矩逐渐减小到零。在旋转点以下，极限土抗力和侧阻抗力矩反向增加到最大值，分别记为1.7F和1.7Ms[7]。另外，桩端水平力Fbu和弯矩Mbu可参考文献[16]方法求得。

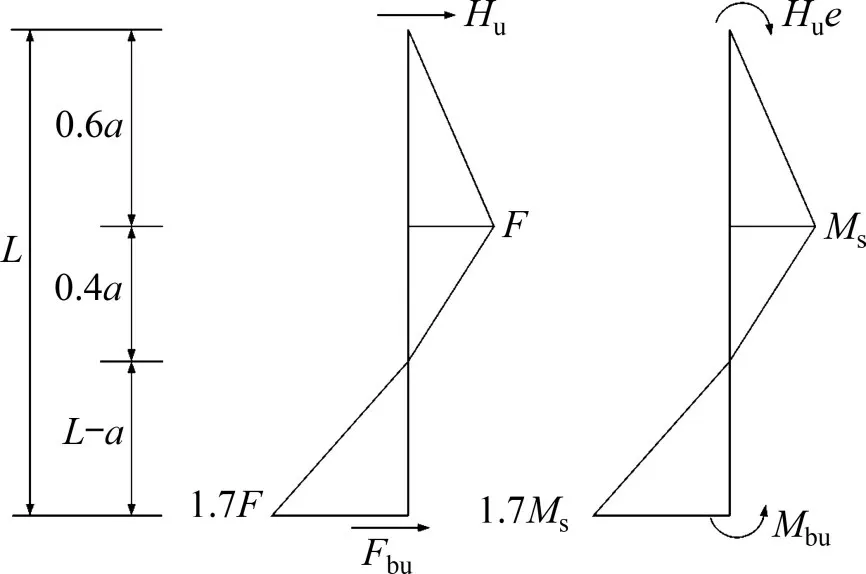
图8 刚性单桩水平极限承载力计算模型Fig.8 Calculation model of lateral ultimate bearing capacity of rigid pile

将z=0.6a分别代入式（11）和（15）可得：

通过水平力平衡建立控制方程：

将式（16）代入式（18）可得

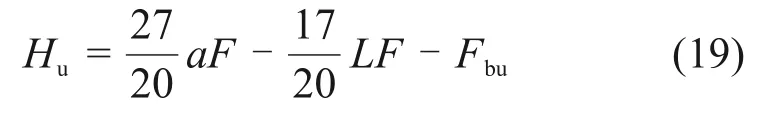
通过力矩平衡建立控制方程：

将式（17）和（19）代入式（20），经处理得到关于旋转点深度a的一元四次方程：

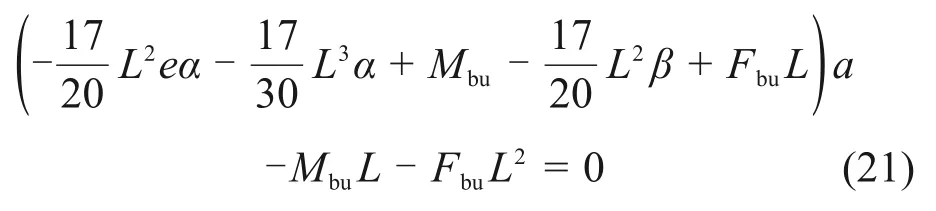
为了方便求解式（21），令：

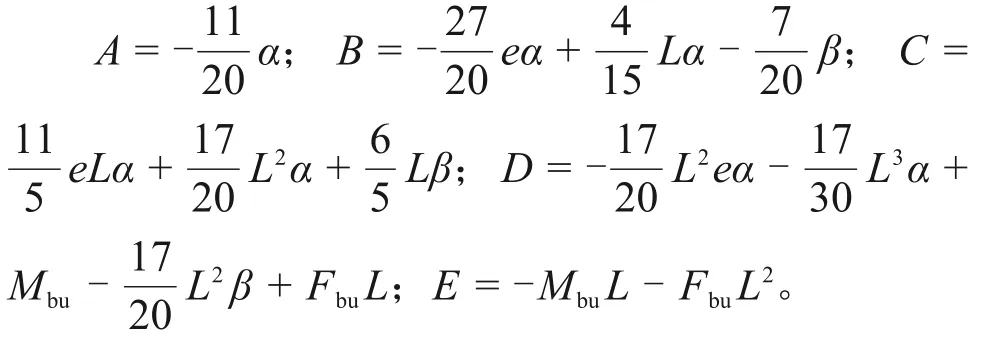
因此，式（21）可简化为

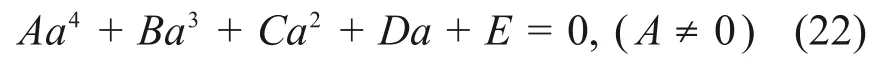
式（22）在复数域内的4 个解分别为a1，a2，a3和a4。再令

并记

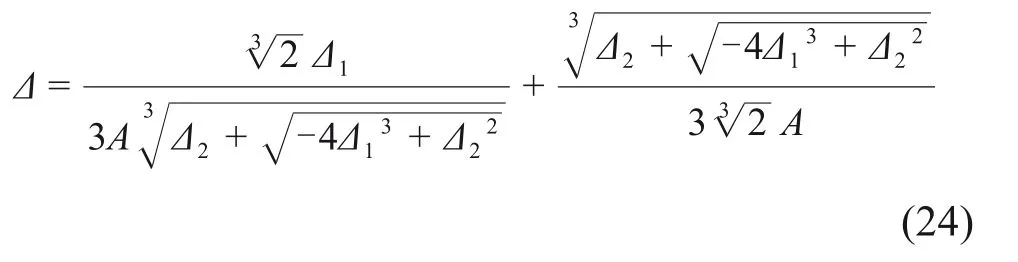
则可分别求得a1，a2，a3和a4：

已有学者对旋转点深度a进行了研究，AHMED 等[17]分析结果表明，a=0.7L～0.78L。基于上述研究成果，通过试算可以确定本文解为a4，将其代入式（19）即得刚性单桩的水平极限承载力Hu：

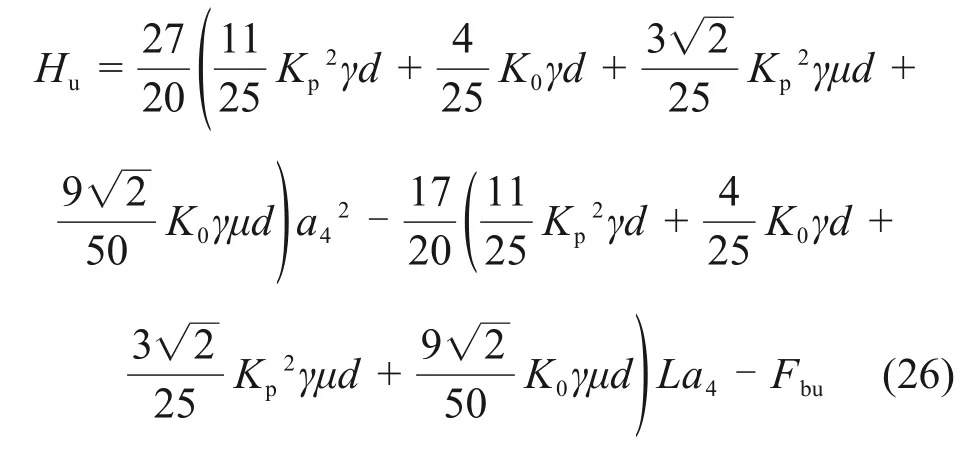
3 方法验证

3.1 极限土抗力的验证

以BARTON 等[18]的离心试验结果Pu,mea为基础，将ZHANG 等[8]、REESE 等[19]、BROMS[3]以及本文方法计算结果Pu,cal进行归一化处理，如图9所示。从图9可以看出：BROMS[3]计算结果偏小，REESE 等[19]计算结果在浅层土体偏小，深层土体偏大。与REESE 等[19]和BROMS[3]方法相比，ZHANG 等[8]同时考虑了径向土压力和环向摩阻力对极限土抗力的贡献，计算精度有所提高，但由于环向摩阻力的分布形式与实际分布差别较大，因此，计算结果仍然偏小。本文不但考虑实际环向摩阻力分布，还考虑竖向摩阻力和环向摩阻力的共同作用，计算结果与试验结果最接近，不考虑两者共同作用将会高估极限土抗力。另外，分别采用本文方法和ZHANG 等[8]方法得到P1/P和P2/P随内摩擦角的变化规律，其结果如图10所示。从图10可以看出：ZHANG等[8]方法得到的P1/P偏大，P2/P偏小，且随着内摩擦角增大，偏差更加明显，这表明ZHANG 等[8]计算方法会高估径向土压力的抗力作用，而低估环向摩阻力的抗力作用。

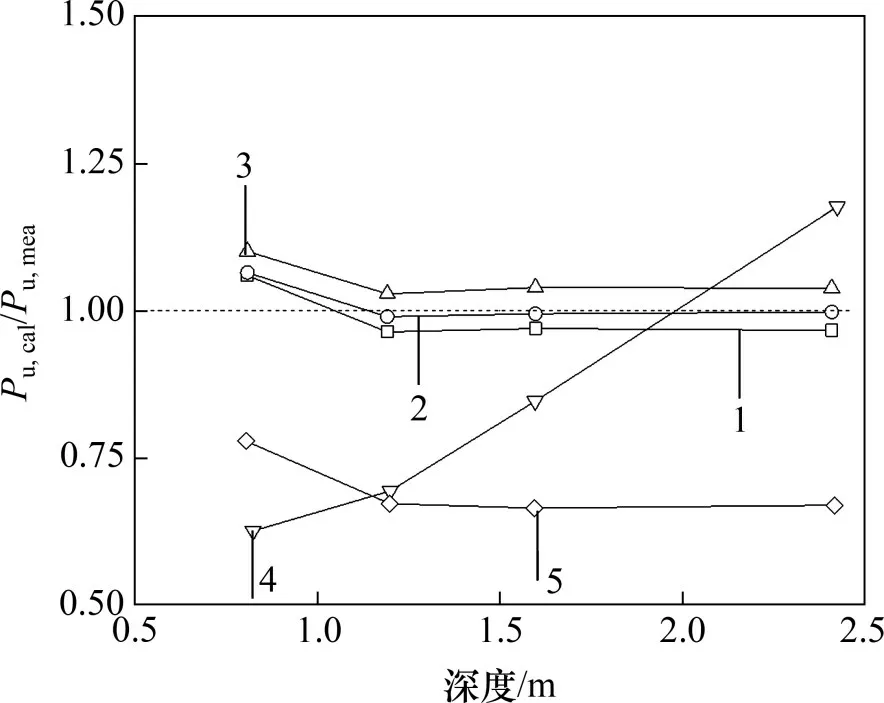
图9 极限土抗力归一化计算结果对比Fig.9 Comparison of normalized calculation results of ultimate soil resistance

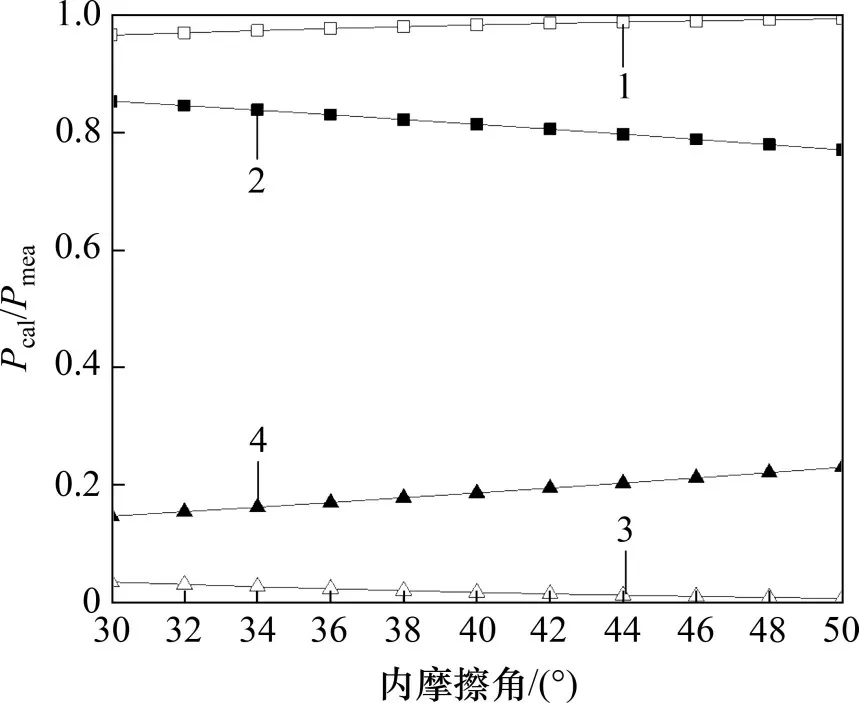
图10 P1/P和P2/P随内摩擦角变化Fig.10 Variation of P1/P and P2/P with angle of internal friction

3.2 侧阻抗力矩的验证

基于YANG等[11]对大直径水平受荷刚性单桩的数值模拟结果，取地面下1 倍桩径深度处进行分析，分别采用本文方法以及竺明星等[12]方法求解被动侧桩周的侧阻抗力矩，结果见图11。从图11可以看出：不考虑竖向摩阻力和环向摩阻力的共同作用，2 种方法均会高估侧阻抗力矩的有利作用。考虑竖向摩阻力和环向摩阻力的共同作用后，计算结果与试验结果误差减小。相比之下，本文计算结果与数值模拟结果变化趋势更一致，且计算精度更高。分析其原因是：竺明星等[12]假定被动侧桩周的径向土压力均匀分布，等于土抗力P与桩径d的比值，这使得桩周α0=0°附近的竖向摩阻力偏小，而显著高估其他位置的竖向摩阻力，本文方法考虑实际径向土压力分布，因此，桩周竖向摩阻力更符合实际。表1所示为被动侧桩周总侧阻抗力矩计算结果。与竺明星等[12]方法相比，采用本文方法可使计算误差由32.74%降低到5.88%。

表1 总侧阻抗力矩计算结果对比Table 1 Comparison of calculation results of total shaft resisting moment

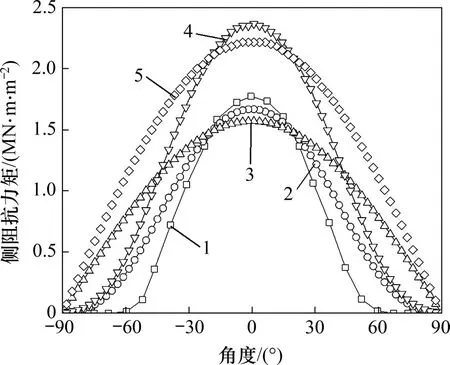
图11 侧阻抗力矩计算结果对比Fig.11 Comparison of calculation results of shaft resisting moment

3.3 水平极限承载力的验证

ADAMS 等[20]、MEYERHOF 等[6,21]和PRASAD等[7]分别通过模型试验研究了刚性单桩的水平极限承载力，模型桩由钢管制作而成。此外，ADAMS等[20]和BHUSHAN等[22]还研究了现场钢筋混凝土钻孔灌注桩的水平极限承载力。根据上述桩土参数，采用本文改进方法对10 个算例进行分析，分为考虑桩身侧阻抗力矩、桩端水平力和弯矩的有利作用与不考虑此有利作用2 种情况，并与ZHANG等[8]计算结果和试验结果进行对比，见表2。图12所示为不同方法计算结果的相对误差。从图12可以看出：在不考虑上述3个因素的有利作用时，与ZHANG 等[8]计算结果相比，采用改进的极限土抗力求解水平极限承载力，计算精度有所提高，但与试验结果相比仍然偏小。而考虑上述3个因素的有利作用时，计算精度显著提高。表3所示为3种方法的平均相对误差，采用本文方法可使平均相对误差由-15.914%减小到2.089%，验证了本文方法的正确性，也表明了在求解水平受荷刚性单桩的极限承载力时，应同时考虑竖向摩阻力与环向摩阻力的共同作用以及侧阻抗力矩、桩端水平力和弯矩对水平极限承载力的贡献。

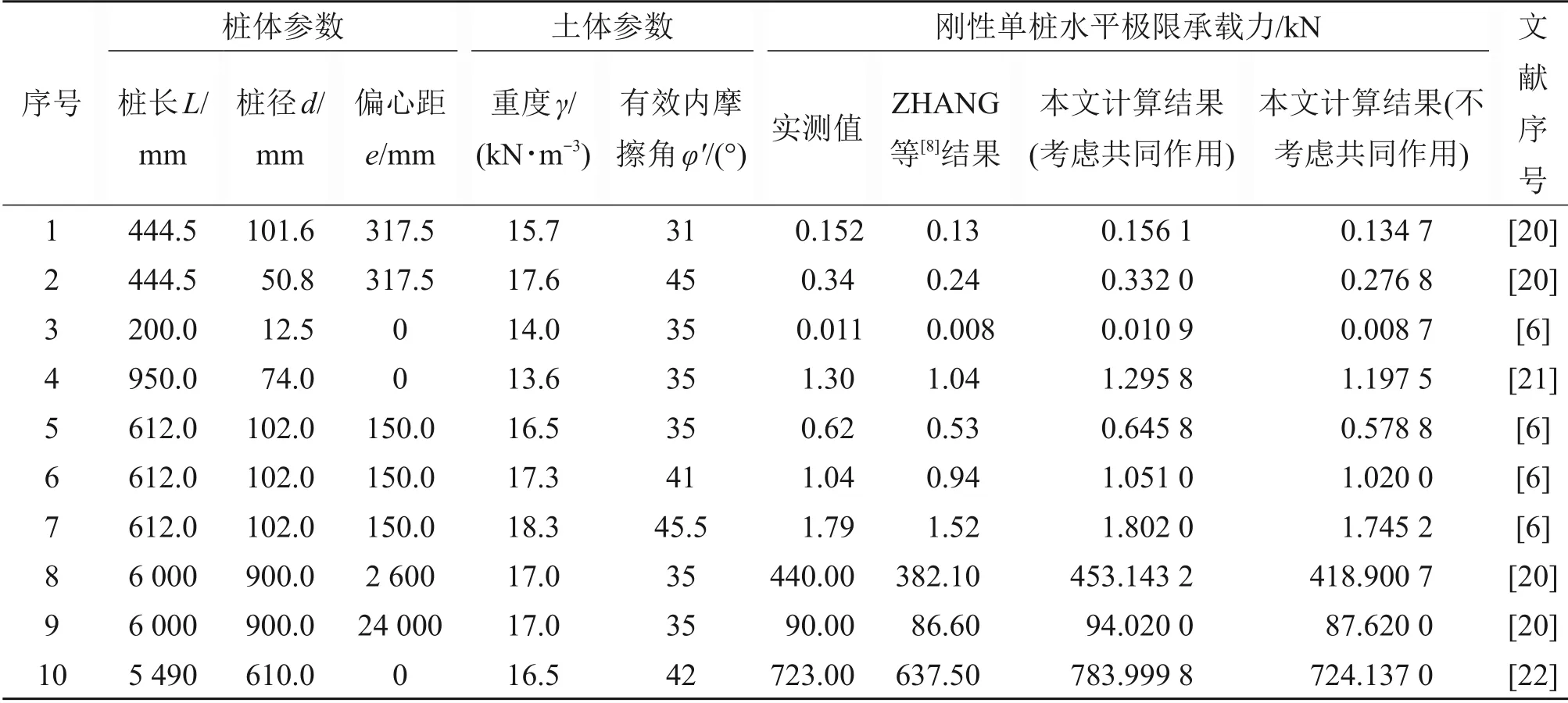
表2 刚性单桩水平极限承载力计算结果对比Table 2 Comparison of lateral ultimate bearing capacity of rigid pile

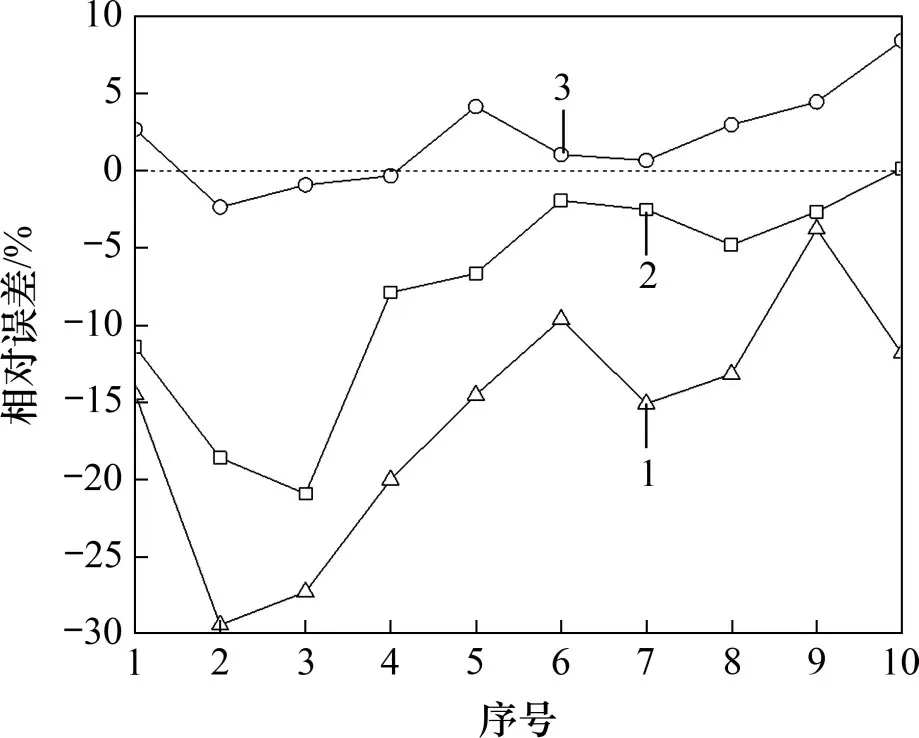
图12 不同方法计算相对误差对比Fig.12 Comparison of relative errors calculated by different methods

表3 平均相对误差对比Table 3 Comparison of average relative error %

4 参数分析

从表2可知：有效内摩擦角、荷载作用点高度、桩埋深、桩径以及土重度等均对刚性单桩的水平极限承载力有影响。因此，以表2中序号8的桩土参数为基础，分别对旋转点深度和水平极限承载力的变化规律进行探讨。另外，为了便于分析有效内摩擦角、土重度、桩埋深以及桩径变化等参数的影响规律，均取荷载作用点高度e=0 进行计算。

4.1 对旋转点深度的影响

旋转点深度的计算结果如图13所示。从图13可见：有效内摩擦角、土重度、桩埋深以及桩径变化对极限状态下刚性单桩的旋转点深度几乎没有影响，而荷载作用点高度e对旋转点深度影响显著；随着e的增大，旋转点深度迅速减小；当荷载作用点高度e大于3 倍桩埋深L时，旋转点深度基本不再变化；在极限状态下，旋转点深度的取值范围为0.65L～0.85L，这与目前的研究成果基本一致[1,17]。综上所述，旋转点深度与荷载作用点高度e密切相关，因此，在求解刚性单桩的水平极限承载力时，应重视荷载作用点高度e对旋转点深度的影响，进而得到更准确的水平极限承载力。

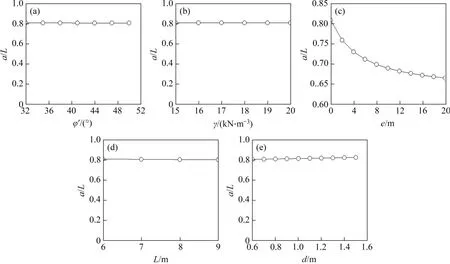
图13 不同影响因素下旋转点深度计算结果Fig.13 Calculation results of depth of rotating point under different factors

4.2 对水平极限承载力的影响

图14所示为不同影响因素下水平极限承载力计算结果。从图14可见：有效内摩擦角对刚性单桩的水平极限承载力影响较大。由图14（a）可以看出：水平极限承载力随有效内摩擦角增大呈指数形式增加，当有效内摩擦角从32°增大到50°时，水平极限承载力增大到了原来的7 倍。由图14（b）可以看出：水平极限承载力随土重度增加呈线性增大，当土重度从15 kN/m3增大到20 kN/m3时，水平极限承载力增加了33%。由图14（c）可以看出：随着荷载作用点高度e的增大，水平极限承载力呈指数减小，当荷载作用点高度大于3 倍桩埋深时，水平极限承载力仅为原来的13%。图14（d）和（e）所示分别为桩埋深和桩径变化对水平极限承载力的影响，可见水平极限承载力均随桩埋深以及桩径的增大而线性增大，且增加桩埋深对提高刚性单桩的水平极限承载力效果更佳。

图14 不同影响因素下水平极限承载力计算结果Fig.14 Calculation results of lateral ultimate bearing capacity under different factors

ZHANG 等[23]指出，在满足给定条件下，单桩发生刚性旋转的条件为：L/T≤2（其中，T=nh,max为水平地基反力系数，EI为桩的抗弯刚度）。海上风电刚性单桩基础荷载作用点高度一般较大，在满足ZHANG 等[23]给出的条件下，应优先选用增加桩埋深的方式来提高水平极限承载力，这既可以发挥增加桩埋深比增加桩径效果更佳的优势，又可以减小荷载作用点高度大的不利影响。

5 结论

1）本文方法能更准确地反映桩周径向土压力和环向摩阻力对极限土抗力的贡献，克服了现有方法的不足。此外，现有方法均未考虑竖向摩阻力和环向摩阻力的共同作用，这会高估极限土抗力和侧阻抗力矩。

2）建立了考虑侧阻抗力矩、桩端水平力和弯矩影响的刚性单桩水平极限承载力计算模型，并给出其解析解，平均相对误差由-15.914%减小到2.089%，计算精度显著提高。因此，在求解水平受荷刚性单桩的极限承载力时，应同时考虑竖向摩阻力与环向摩阻力的共同作用以及侧阻抗力矩、桩端水平力和弯矩对水平极限承载力的贡献。

3）海上风电刚性单桩基础荷载作用点高度一般较大，应优先选用增加桩埋深的方式来提高水平极限承载力，这既可以发挥增加桩埋深比增加桩径效果更佳的优势，又可以减小荷载作用点高度大的不利影响。