变论域双模糊算法在铝电解槽电压滤波中的应用研究
2021-11-25邓联文蒋海斌赵岩刘国涛陈鸿飞罗衡
邓联文,蒋海斌,赵岩,刘国涛,陈鸿飞,罗衡
(1.中南大学物理与电子学院,湖南长沙,410083;2.湖南力得尔智能科技有限公司,湖南长沙,410006)
随着电解铝工业的发展,铝电解过程的智能控制和专家控制系统[1]成为研究热点。电解槽电压是唯一能在线实时测量并反映槽状态的参数,因此,对电解槽电压尽可能快速进行滤波跟踪分析至关重要。对槽电压信号进行分析应尽可能即时获取电解槽运行的状态信息,这有利于及时预防和处理电解槽的不正常工作状态(如电解槽阳极效应),估计电解质中氧化铝浓度变化,从而为调控进料量提供参考依据,提高电解铝效率和节约能源。目前,在电解铝工业中应用的滤波算法是固定滤波系数的一阶滤波算法,难以兼顾算法平稳度和灵敏度。除了使用传统的滤波方法外,人们还使用模糊算法[2-12]获取滤波系数,或使用双模糊算法[13-14]获取滤波系数和校正系数。在电解槽电压变化量较大时,这些算法的滤波跟踪能力不强。使用输入变量论域可变的隶属函数[15]可提高模糊算法的精度。本文拟设计一种变论域双模糊算法,获取并调整一阶滤波器的系数和校正系数。该算法具有抗干扰能力强、响应速度快等优点,对参数变化有较强的鲁棒性。
1 滤波算法设计
1.1 电解槽电压滤波算法
现阶段采用具有惯性滤波性能的一阶滤波算法,滤波算法的数学模型为:
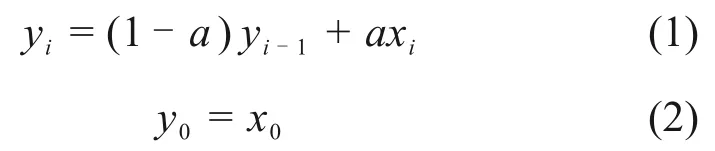
式中:yi为i时刻的电解槽电压滤波值;xi为i时刻的电解槽电压测量值;yi-1为i-1时刻的电解槽电压滤波值;x0为电解槽电压测量初始值;y0为电解槽电压滤波初始值;a为滤波系数。电解槽电压采样频率为1 Hz,电解槽电压频率范围为0.002~0.040 Hz,噪声频率约为0.03 Hz[16]。为有效滤除噪声,滤波系数a取定值,为1/32。该算法在电解槽电压变化量较小时滤波效果好。受生产工艺影响(如电解槽Al2O3缺少)、当电解槽电压变化量较大时,电压信号偏向于0.005~0.040 Hz频段,由于滤波系数小,通频带窄,此频段的电压信号衰减最高达-20 dB,算法灵敏度低,迟滞性严重,不能满足电解槽电压滤波要求。
1.2 改进的滤波算法
针对固定系数一阶滤波算法在电解槽电压变化量大时滤波器通带窄、迟滞性严重、灵敏度低等问题,本文设计滤波系数αi可变的一阶低通滤波器。为有效滤除噪声,提高滤波算法的滤波性能,设计校正系数βi可变的校正方程。对式(1)和(2)进行改进,得到如下滤波算法系统模型:

式中:xi为i时刻电解槽电压;xi为i-1 时刻电解槽电压;为校正后i时刻电解槽电压;-1为校正后i-1时刻电解槽电压;x′i为滤波后i时刻的电解槽电压;Δxi为i时刻电解槽电压与i-1 时刻电解槽电压的变化量;dxi为第i时刻电解槽电压与校正后i-1 时刻的电压的变化量;αi∈[0,1],为变论域模糊控制器计算的可变的滤波系数;βi∈[0,1],为变论域模糊控制器计算的可变校正系数。
2 变论域双模糊控制
2.1 变论域双模糊控制器的工作原理
变论域双模糊算法工作原理如图1所示,双模糊算法有2个模糊控制器。图1中,虚线框为模糊控制器1,输入量为Δxi和dxi,输出为i时刻滤波系数αi;实线框为模糊控制器2,输入量为Δxi和dxi,输出为i时刻校正系数βi;右上侧为改进的滤波算法中滤波器,用于计算x′i;右下侧为改进的滤波算法中校正方程,用于计算。图1中论域伸缩环节主要功能是对输入量论域压缩或扩张,当输入量Δxi或dxi较小时,压缩论域,当输入量Δxi或dxi较大时,扩张论域。

图1 变论域双模糊控制结构图Fig.1 Structure diagram of variable universe double fuzzy control
2.2 变论域双模糊算法设计
在电解过程中,电解槽电压变化幅值易受工艺参数变化影响,常规的固定论域以及与之对应的固定模糊判决规则的模糊控制有较大局限性。当选择的论域范围较小时,输入输出的调节范围会超出所选择的论域范围,从而导致系统超调,控制效果不理想;当选择的论域范围较大且模糊控制器输入量较小时,输入输出可使用的模糊规则数量减少,导致输入输出所使用的模糊规则的数量降低,控制精度下降。变论域模糊控制方法与常规模糊控制算法的主要区别是其基本论域能根据输入量差值的变化而变化。变论域是依据伸缩因子改变论域[17]。收缩因子函数f(x)表达式为
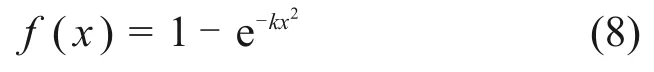
式中:k为实际应用中的可设计参数。电解槽在正常工作状态下,电压大约为4 V,当电解槽电压大于8 V 时,电解槽发生阳极效应,所以,不分析8 V 以上的电解槽电压,且电解槽电压波动一般不超过4 V,本文中输入变量的初始论域为[0,E],其中,E=4。当输入变量Δxi和dxi在区间[0,1]时,论域为初始论域的25%,即论域为[0,1],此时,f(x)=0.25,x=1,代入式(8)得k=0.287。依此类推可得变量x={Δxi,dxi}与参数k的关系,如表1所示。

表1 收缩函数参数kTable 1 k of shrink function parameter
由表1可知:当输入变量值在不同区间时,收缩函数参数k取不同值。Δxi和dxi的初始论域为[0,E],根据收缩原理,Δxi通过论域收缩后,论域范围可变换为[0,f(Δxi)E],dxi通过论域收缩后,论域范围可变换为[0,f(dxi)E]。可变论域的输入变量隶属函数如图2(a)所示。输出变量αi和βi的论域为[0,1],输出变量的隶属函数如图2(b)所示。
图2中,输入变量和输出变量都采用幅值为1的三角隶属函数。输入变量和输出变量模糊子集为{S(小),SM(小中),M(中),MB(中大),B(大)},{Δxi,dxi,αi,βi}={S,SM,M,MB,B},模糊控制器根据输入量决定模糊控制器的输出量。若Δxi和dxi小,则模糊控制器1 输出αi小;若Δxi和dxi大,则模糊控制器1 输出αi大;若Δxi和dxi小,则模糊控制器2输出βi小;若Δxi和dxi大,则模糊控制器2 输出βi大。以此可推出25 条模糊控制规则。

图2 模糊输入输出隶属函数Fig.2 Input and output membership function
模糊控制器1:
IF Δxi=S and dxi=S,THENαi=S;
IF Δxi=B and dxi=B,THENαi=B。
模糊控制器2:
IF Δxi=S and dxi=S,THENβi=S;
IF Δxi=B and dxi=B,THENβi=B。
模糊控制器1和模糊控制器2均能得出25条控制器模糊规则(如表2所示),组成图1中的模糊规则库。模糊控制器1完成模糊推理后,采用重心解模糊[18]获得精确控制量αi;模糊控制器2 完成模糊推理后,采用重心解模糊获得精确控制量βi。
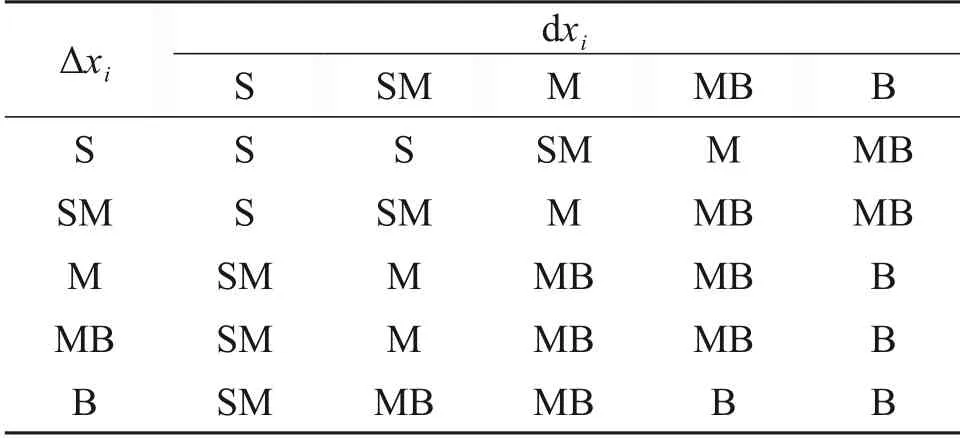
表2 模糊规则表Table 2 Fuzzy rules table
3 仿真与结果分析
3.1 电解槽电压跃变滤波比较
电解槽电压由ADC 转换计算得出,本文取200个电压数据,采样频率为1 Hz。在50 s时调节电压幅度上升1 V,在100 s 时调节电压幅度下降1 V。分别用一阶滤波、模糊算法滤波(无校正系统模块)、双模糊算法滤波、变论域双模糊算法对200个实验数据滤波仿真结果进行分析、比较。电压跃变滤波波形见图3。

图3 电压跃变滤波波形Fig.3 Voltage sudden filtered waveform
分析图3可知:在电压变化量小时(如40~50 s时的电压区间),一阶滤波算法、模糊算法、双模糊算法、变论域双模糊算法效果均理想,50 s时电压幅值上升1 V,第100 s时电压幅值下降1 V,电压变化量较大,一阶滤波算法的滤波系数小,故迟滞严重,跟踪能力弱。系统的均方根误差与跟踪时间见表3。从表3可见:模糊算法通过1 个模糊控制器由电压变化获取滤波系数,滤波跟踪时间比一阶滤波缩短70%;双模糊算法通过2个模糊控制器由电压变化分别获取滤波系数和校正系数,滤波跟踪时间比一阶滤波缩短85%;变论域双模糊算法在双模糊控制器基础上对模糊控制器的输入量论域进行伸缩后,通过2个模糊控制器分别获取滤波系数和校正系数,滤波跟踪时间比一阶滤波缩短93%。
滤波算法的均方根误差越小,说明滤波算法性能越好。由表3可知变论域双模糊算法均方根误差最小,表明变论域双模糊算法比其他3种方法有更好的滤波效果。
3.2 电解槽电压波动时滤波比较
具有强跟踪性的滤波算法可提高效应预报的准确率,阳极效应智能预报[19]是现代铝电解控制中一种最有效的预防电解槽效应方法,是通过滤波后的电解槽电压计算电解槽电压斜率,智能预报电解槽阳极效应。用4 种不同滤波方法对某铝厂500 kA 系列电解槽中1 台电解槽电压进行滤波处理。一阶滤波、模糊算法、双模糊算法和变论域双模糊算法对电解槽电压滤波仿真结果见图4。从图4(a)可见:在60~70 s 时,电解槽电压波动小,一阶滤波算法在此区间的均方根误差为25 mV,模糊算法在此区间的均方根误差为20 mV,双模糊算法在此区间的均方根误差为19 mV,变论域双模糊算法在此区间的均方根误差为17 mV,4种电压滤波方法在此时间段滤波效果均很好,其中,变论域双模糊算法滤波效果最好。从图4(b)可见:当电解槽电压为80~90 s 时,区间槽电压波动较大,一阶滤波算法在此区间的均方根误差为382 mV,模糊算法在此区间的均方根误差为326 mV,双模糊算法在此区间的均方根误差为307 mV,变论域双模糊算法在此区间的均方根误差为150 mV。实验结果表明,变论域模糊算法在电解槽电压波动量小时算法平稳度好,在电解槽电压波动量大时跟踪性强,灵敏度高,滤波效果最优。

图4 电解槽电压滤波波形Fig.4 Voltage filtering waveforms of electrolytic cell
电解槽电压波动量较小时的滤波系数与校正系数见图5,其中,图5(a)所示为变论域双模糊算法、双模糊算法、模糊算法与一阶滤波算法在电解槽电压波动量小条件下进行电解槽电压滤波的滤波系数变化曲线,图5(b)所示为变论域双模糊算法、双模糊算法在电解槽电压波动量小条件下的校正系数变化曲线。从图5可见:在电解槽电压波动量小时,滤波系数较小,为0.1左右,此时,滤波算法的校正系数较小,可以得到平稳的滤波效果。
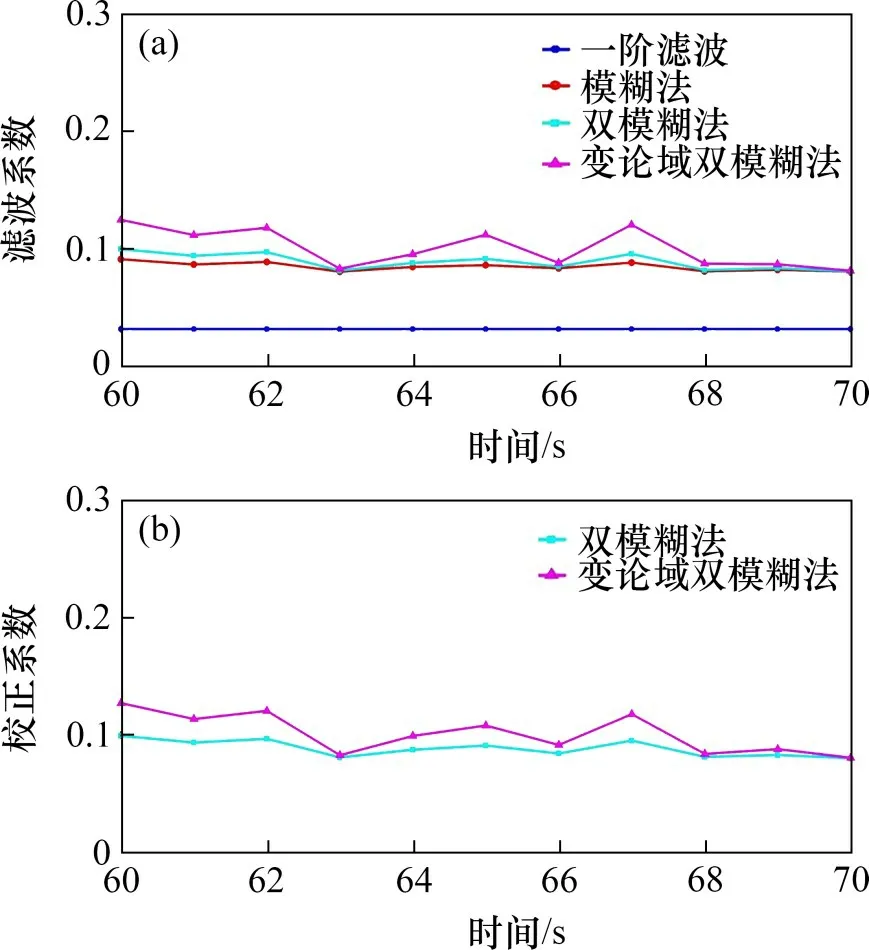
图5 电解槽电压波动量较小时的滤波系数与校正系数变化曲线Fig.5 Varied curves of filter coefficient and correction coefficient when electrolytic cell voltage fluctuation is small
电解槽电压波动量较大时的滤波系数与校正系数见图6,其中,图6(a)所示为变论域双模糊算法、双模糊算法、模糊算法与一阶滤波算法在电解槽电压波动量大条件下进行电解槽电压滤波的滤波系数变化曲线,图6(b)所示为变论域双模糊算法、双模糊算法在电解槽电压波动量大条件下校正系数变化变化曲线。从图4(b)可见:在80~90 s时,电压波动较大且在85 s时电解槽电压变化量较大,为0.697 V。由图6可见:在80~90 s 时,模糊算法、双模糊算法和变论域双模糊算法的滤波系数呈变大趋势,且都在85 s时达到最大值,分别为0.198 9,0.240 6 和0.663 2;双模糊算法和变论域双模糊算法的校正系数也呈变大趋势,在85 s时分别达到0.240 6 和0.694 4,此时,滤波算法校正系数和滤波系数最大,可以获得跟踪性强的滤波效果。
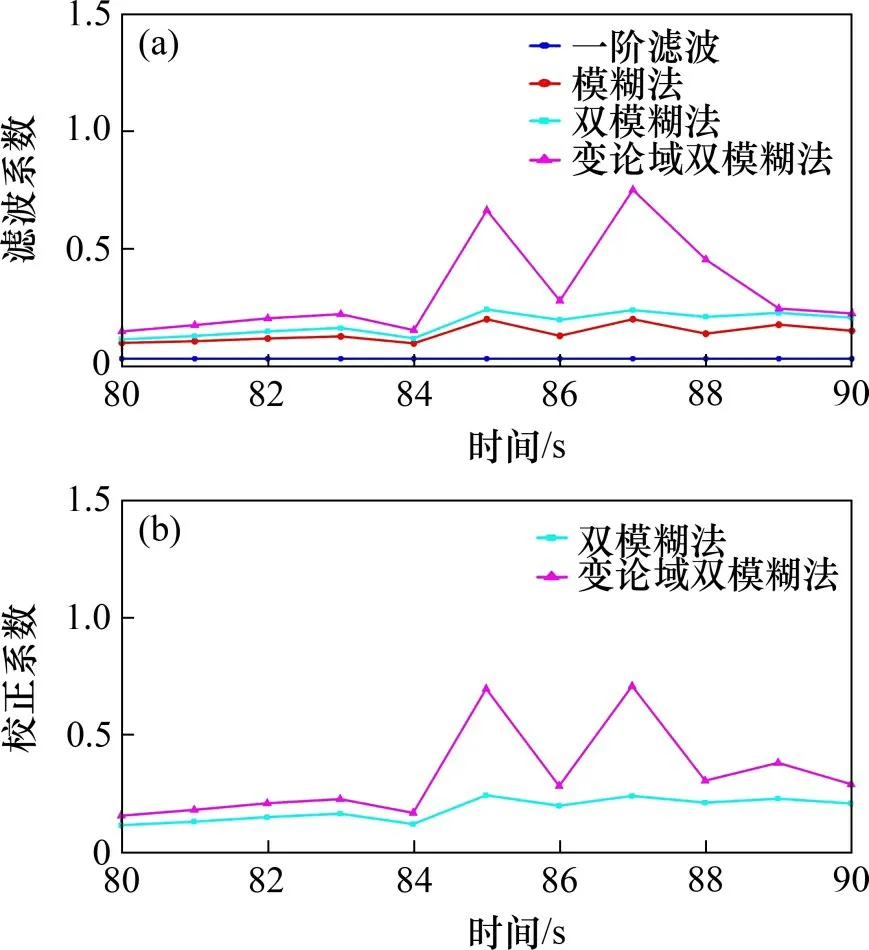
图6 电解槽电压波动量较大时的滤波系数与校正系数变化曲线Fig.6 Varied curves of filter coefficient and correction coefficient when electrolytic cell voltage fluctuation is large
电解槽电压与不同算法滤波电压的差值见表4,其中,η1为电解槽电压与一阶滤波算法滤波后电压的差值,η2为电解槽电压与模糊算法滤波后电压的差值,η3为电解槽电压与双模糊算法滤波后电压的差值,η4为电解槽电压与变论域双模糊算法滤波后电压的差值,γ1为一阶滤波电压,γ2为模糊算法滤波电压,γ3为双模糊算法滤波电压,γ4为变论域模糊算法电压,xi为电解槽电压,t1为时间。由表4可知:84 s 与85 s 时的电解槽电压差值为697 mV,一阶滤波法得出85 s 时的滤波电压为4 025.1 mV,与电解槽电压差值为791.7 mV;模糊算法滤波得出85 s时滤波电压为4 218.1 mV,与电解槽电压差值为601.9 mV;双模糊算法滤波得出85 s时滤波电压为4 260.4 mV,与电解槽电压差值为559.6 mV;变论域双模糊算法滤波得出85 s 时滤波电压为4 602.0 mV,与电解槽电压差值为218 mV。结合上述分析,可知变论域双模糊算法不仅在数据变化量小时算法平稳度好,而且在电解槽电压变化量大时灵敏度高,跟踪性强。

表4 电解槽电压与不同算法滤波电压的差值Table 4 Difference between electrolytic cell voltage and filtering voltage of different algorithms
实验结果表明:变论域双模糊算法能根据电解槽电压波动量自适应地改变滤波系数;当电解槽电压波动量较小时,滤波系数变小;当电解槽电压波动量大时,滤波系数变大。变论域双模糊算法有效解决了滤波算法在电解槽电压变化量大时跟踪性差的问题;校正系数也能根据电解槽电压变化量发生改变,极大地增强了滤波效果。
4 结论
1)研究了一种基于一阶滤波算法改进的自适应滤波器,对电解槽电压进行滤波。分析了相邻电解槽电压变化量以及电解槽电压与校正后电压的变化量,设计了一种输入变量论域可变的改进的双模糊控制系统。变论域双模糊控制器分别控制滤波系数与校正系数变化,滤波系数和校正系数在滤波过程中自适应获得最优取值。
2)变论域双模糊法优化的滤波算法跟踪时间比双模糊法优化的滤波算法跟踪时间缩短54%,比模糊法优化的滤波算法跟踪时间缩短77%,比一阶滤波算法的跟踪时间缩短93%;变论域双模糊法优化的滤波算法的均方根误差比双模糊法优化的滤波算法减小74%,比模糊法优化的滤波算法减小82%,比一阶滤波算法减小93%。该算法可极大地提高阳极效应预报的准确率,对电解铝节约电能、提高电解效率具有重大意义。
