DT-Ⅲ型扣件系统弹条疲劳特性及优化研究

宋子洋，卢俊，胡世斌，陈明明，赵才友

（1.高速铁路线路工程教育部重点实验室，四川成都，610031；2.西南交通大学土木工程学院，四川成都，610031；3.重庆市轨道交通（集团）有限公司，重庆，401120）

随着轨道交通的高速发展，扣件系统为轨道结构提供的作用不仅仅局限在弹性支承和保持轨距等方面，扣件系统受到的荷载情况也越来越复杂，人们对其服役要求也越来越高。近年来，扣件系统弹条在服役过程中频繁地出现断裂现象，这种现象往往发生在波磨突出段或曲线段。弹条的服役状态直接影响到扣件系统的支承刚度和服役寿命，甚至影响到行车的安全性和稳定性。如何让弹条服役寿命得到改善，引起了众多学者的关注和探讨。

国内外学者对弹条服役情况进行了研究。伍曾等[1]从蠕变影响下的扣压力损失角度探讨了弹条的服役性能变化情况。余自若等[2]研究了疲劳荷载作用下X2 弹条的疲劳寿命及疲劳破坏危险点位置。刘玉涛[3]对有无钢轨波磨下高速铁路WJ-7 扣件系统动力响应进行分析，研究了钢轨波磨下扣件弹条疲劳破坏的机理，并计算了弹条危险点处的疲劳寿命，但是影响因素考虑不够全面，比如轨距块对弹条力学响应影响。辛涛等[4]建立扣件精细分析模型计算得到扣件弹条应力应变时程曲线，结合疲劳分析方法和累积损伤理论，采用Seeger算法对弹条的疲劳寿命进行分析。XIAO 等[5]建立了精细化扣件系统模型并对其进行服役状态下模态和谐响应分析，结合现场实测弹条振动加速度，进行了疲劳分析，其认为钢轨波磨引起弹条共振是弹条断裂的主要原因。FERREÑO 等[6]结合疲劳试验和有限元方法对SKL-1型弹条进行疲劳预测，同时分析了弹条材料热处理工艺和现场安装精度的合理性。可以看出目前对弹条的力学特性研究集中在应力应变、振动加速度和疲劳寿命分析，但是对于弹条断裂现象没有提出针对性改进意见。现有的针对弹条断裂问题的改进处理措施一方面是针对弹条的断口宏微观观察和金相组织检查等，以此减少弹条组织缺陷[7-8]；另一方面是针对弹性垫板和绝缘阻尼块等零部件的材料特性作出改进，通过静动力计算来判断改进效果[3,9-12]。但对于改进措施后弹条的疲劳寿命[13]等服役性能的影响缺乏研究，没有进一步验证其意见合理性。

本文作者针对深圳地铁弹条断裂频发的现象，先对DT-Ⅲ型扣件系统进行静力、动力学分析，同时提出并验证一系列改进措施对弹条的影响。在此基础上，再通过多体动力学和有限元结合的方法，分析上述不同改进方法下波磨幅值对弹条动力响应的变化规律。最后，对弹条的疲劳寿命进行改进前后对比计算。

1 DT-Ⅲ型扣件系统

1.1 有限元模型

DT-Ⅲ型扣件系统由轨下垫板、轨距块、III型弹条、铁垫板、板下垫板以及道钉等主要部件组成，其几何模型见图1（a）。根据扣件系统三维实体模型，建立扣件系统精细化有限元模型。建模时，考虑到几何模型的复杂性，在对结果影响不大的前提下，对混凝土短轨枕、轨下垫板、铁垫板及板下垫板、轨距块进行必要的简化。有限元模型如图1（b）所示。

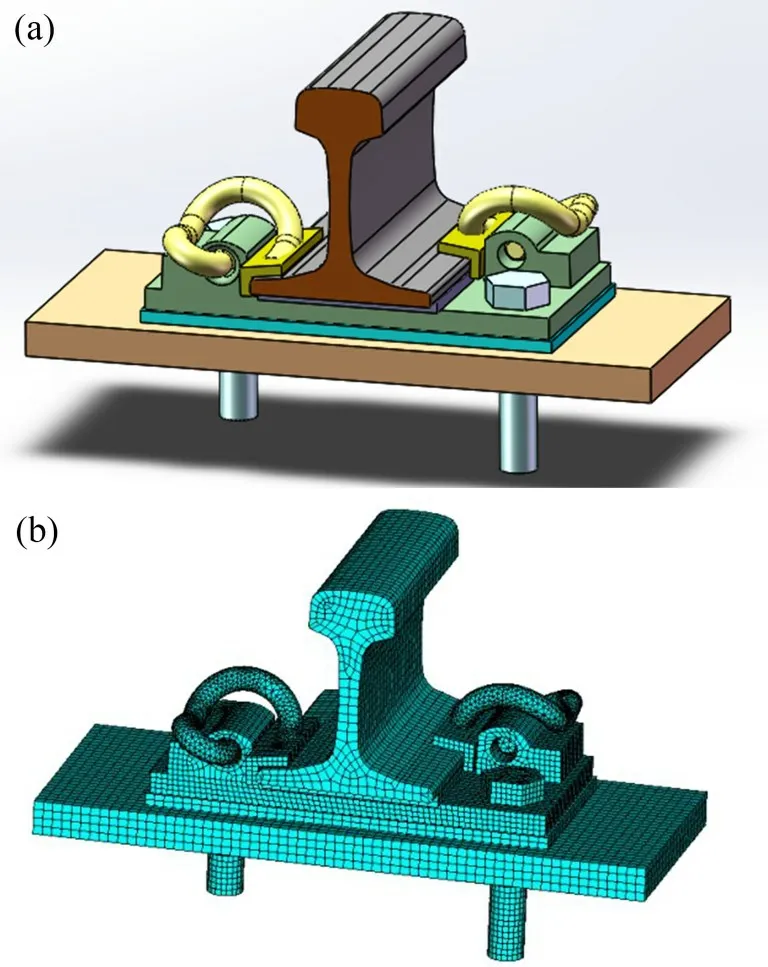
图1 DT-III型常阻力扣件系统Fig.1 DT-III constant resistance fastener system

1.2 边界条件与材料参数

根据Ⅲ型弹条扣件系统的实际工作状态，以尽量模拟扣件系统弹条的真实受力状况为原则，确定有限元模型的边界条件。模拟真实弹条工作状态下的接触条件，各接触对设置如表1所示，接触方式均为面-面接触，并且接触算法选用增广Lagrange法。其他部件之间通过黏接命令进行黏结绑定。

表1 接触对参数Table 1 Contact parameters

考虑到随着弹条中肢插入铁垫板插孔深度的增大，弹条会发生局部的塑性变形，简单选用理想弹性模型并不能真实地模拟弹条的受力状态，因此需要考虑弹条材料的塑性变形，进行非线性分析。

根据GB/T 1222—2007“弹簧钢”标准要求，弹条材料的屈服强度σs=1 375 MPa，抗拉强度σb=1 570 MPa，强化模量取为0.1E（E为弹性模量）。并选择第四强度理论（Mises 准则）作为准确分析弹条应力和应变的评价指标。弹条材料设置为理想线性强化弹塑性，如图2所示。模型中各个部件的材料属性如表2所示。

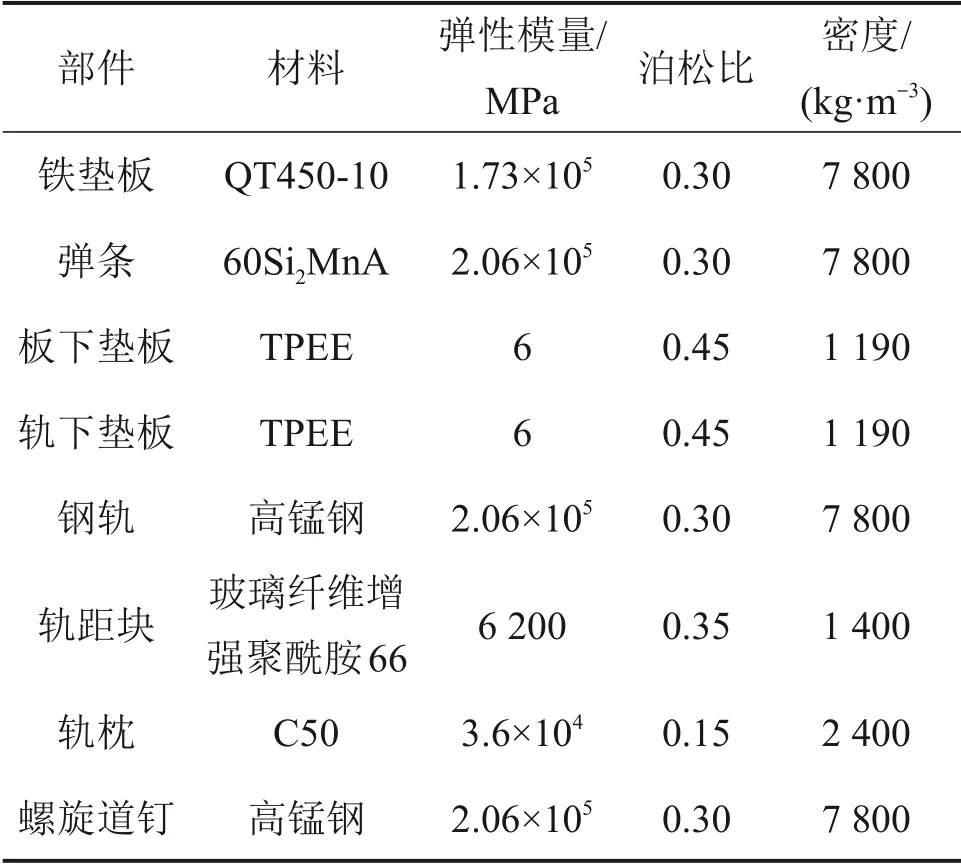
表2 各部件材料参数Table 2 Material parameters of each component

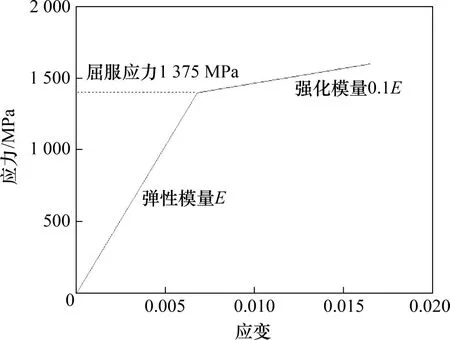
图2 理想线性强化弹塑性模型Fig.2 Ideal linear hardening elastic-plastic model

2 弹条静态应力分析

2.1 服役状态下弹条应力

基于上述有限元模型，在弹趾与轨距块的接触对中，使接触面“移动”至轨距块上表面，以模拟弹条的安装过程。计算结果如图3所示。由图3可知：正常安装状态下弹条的最大等效应力为1 400 MPa，发生在后拱小圆弧内侧，与弹条的实际断裂位置相符。

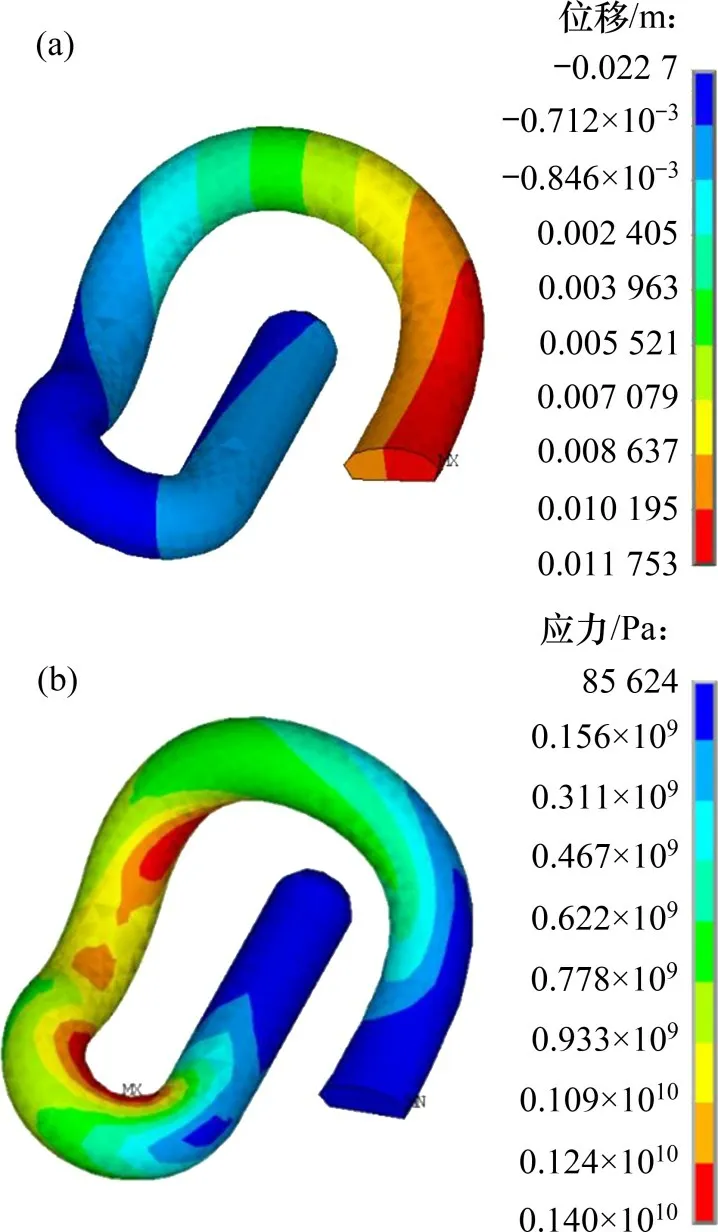
图3 正常安装状态下计算结果Fig.3 Calculation results under normal installation

由Q/CR 565—2017“弹条III 型扣件”提出的技术要求，在正常安装状态下，弹条后端小圆弧内侧与铁垫板端部的距离应在8～10 mm 范围内。但由于实际安装过程中的人工安装误差，通常存在弹条过安装的现象。当弹条后端小圆弧内侧与铁垫板端部的距离由8 mm 减小到1 mm 时，弹条后端的最大等效应力由原来的弹条后端外侧圆角转移到内侧圆角。最大等效应力发生在弹条后拱内侧单元集，如图4所示。

图4 插入深度1 mm对弹条最大等效应力发生位置的影响Fig.4 Influence of inserting depth to 1 mm on position of maximum equivalent stress of clips

当弹条后端小圆弧内侧距铁垫板插入孔端面较小时，弹条后拱接近中肢的区域与铁垫板发生挤压，接触状态由之前的线接触转变为点接触，造成局部应力集中，超过屈服强度，从而在弹条后端圆弧与铁垫板接触处表层出现塑性变形，如图5所示。

图5 弹条中肢与铁垫板插孔间接触斑大小和位置Fig.5 Size and location of indirect contact spot between fastener clips middle leg and iron base plate socket

2.2 优化措施下弹条静态应力

考虑到弹条在工作过程中可能出现的局部应力集中后的疲劳断裂现象，本文一方面对弹条进行打磨，改进为高频弹条；另一方面对绝缘轨距块进行参数化改进研究。高频弹条指通过提高弹条的固有频率，使弹条的固有频率大于钢轨波磨的激振频率，以避免弹条发生共振。提高弹条固有频率的方法是对弹条跟端进行打磨，跟端打磨区域见图6。轨距块主要起绝缘和传递钢轨振动、抵抗横向力的作用，对轨距块的改进方法主要是材料参数和结构尺寸的优化。

图6 弹条跟端打磨3 mmFig.6 Grinding of fastener clips heel 3 mm

2.2.1 高频弹条静态应力

图7所示为跟端打磨3 mm 后弹条应力计算结果。跟端打磨3 mm及跟端未打磨的计算结果见表3。由图7和表3可知：跟端打磨3 mm后弹条的最大等效应力为1 400 MPa，扣压力为11.7 kN，与未打磨弹条相比，其最大等效应力及扣压力基本无变化，而最大等效应力的位置由后拱小圆弧转移到后拱小圆弧靠近跟端处（见图7）。

表3 高频弹条对弹条静态受力的影响Table 3 Influence of high frequency fastener clips on static stress of elastic strip

图7 跟端打磨3 mm应力计算结果Fig.7 Stress calculation results of grinding heel for 3 mm

2.2.2 轨距块对弹条静态应力影响

轨距块与弹条直接接触，其变形以及厚度直接影响弹条的扣压力，进而引起一系列影响。计算时，轨距块弹模分别取6 200，3 000，1 500，1 000和500 MPa，其他部件材料参数见表2，分析不同轨距块弹性模量对弹条受力的影响，结果见表4。轨距块厚度分别为8，6 和4 mm，分析不同轨距块厚度对弹条受力的影响，结果见表5。

表4 轨距块弹性模量对弹条静态受力的影响Table 4 Influence of elastic modulus of gauge block on static stress of fastener clips

表5 轨距块厚度对弹条静态受力的影响Table 5 Influence of gauge block thickness on static stress of fastener clips

由计算结果可知：随着轨距块弹性模量增大，弹条趾端的位移增大，扣压力和最大等效应力也随之变大；轨距块弹性模量从500 MPa 增大到6 200 MPa，弹条最大等效应力从1 370 MPa 增大到1 400 MPa，且最大应力均发生在弹条后拱小圆弧处。随着轨距块厚度的减小，弹条的最大等效应力以及扣压力均随之减小。经分析可知，轨距块厚度的降低使弹条的弹程减小，进而导致弹条扣压力以及最大等效应力的降低，但在这3种情况下，弹条最大等效应力均发生在后拱小圆弧内侧，说明轨距块厚度不会改变弹条最大等效应力的发生位置。

3 弹条频域分析

3.1 Ⅲ型弹条频响分析

为探究弹条的振动特性，探明弹条在自由状态下在哪些频段下的振动最容易被激发出来，有必要对其进行频响分析[14-15]。分析中，在趾端下表面施加一个方向垂直向上的正弦激励荷载，荷载频率为10～2 000 Hz。重点关注弹条断裂位置的频响计算结果，即后拱小圆弧内侧靠近中肢位置。选取弹条后拱小圆弧加速度导纳作为评价指标，如图8所示。

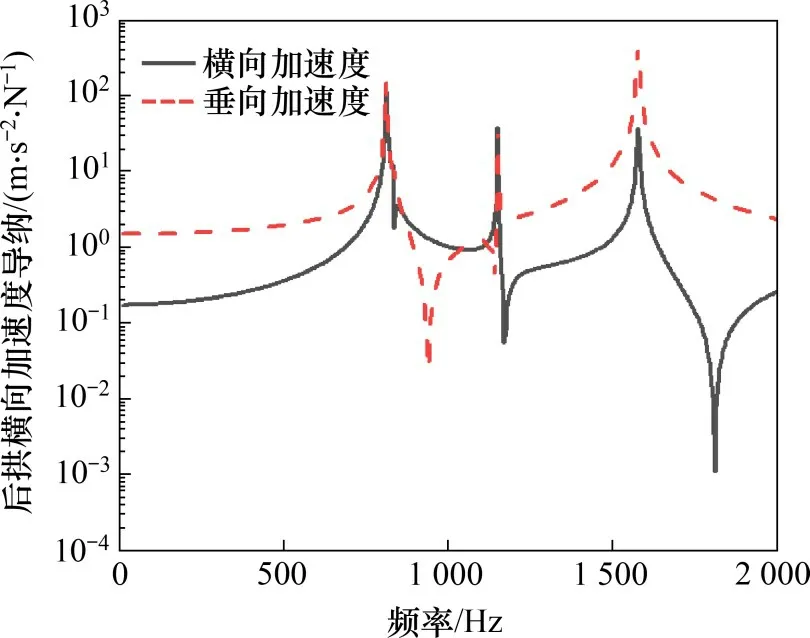
图8 III型弹条后拱加速度导纳Fig.8 Acceleration admittance of rear arch of type III fastener clips

从频响结果可看出：弹条各部位的垂横向加速度导纳均出现4个比较明显的共振峰，对应频率分别为811，833，1 115 和1 515 Hz，说明在10～2 000 Hz激扰源激励下，此四阶频率容易被激发出来，造成弹条相应部位垂横向加速度增大。故当扣件受到该频率的激振作用时，弹条发生共振，并引起弹条的断裂。

3.2 服役状态模态分析

为进一步研究弹条在工作时的振动特性，对弹条正常安装状态进行模态分析，计算可得其固有频率及振型描述如表6所示。在正常安装状态下，III型弹条的第一阶振型如图9所示。

图9 III型弹条服役状态下第一阶振型Fig.9 The first mode shape of type III fastener clips in service

表6 III型弹条服役状态下前四阶固有频率及振型描述Table 6 Description of the first-four natural frequencies and vibration modes of type III fastener clips in service

3.3 优化措施对弹条模态影响

3.3.1 高频弹条对弹条模态影响

对跟端打磨3 mm 的高频弹条进行模态分析，其在正常安装状态下的前四阶固有频率以及相应的振型描述如表7所示。在正常安装状态下，高频弹条的第一阶振型如图10所示。

图10 打磨3 mm服役状态下第一阶振型Fig.10 The first mode shape in service after 3 mmgrinding

表7 打磨3 mm弹条下前四阶固有频率及振型描述Table 7 Description of the first four natural frequencies and vibration modes under polished 3 mm fastener clips

由表7可知：与未打磨相比，跟端打磨后弹条的前四阶固有频率均有所提高。其中，弹条的第一阶固有频率从333 Hz提高到358 Hz，增大了25 Hz；第二阶固有频率从524 Hz 提高到690 Hz，增大了166 Hz；第三阶固有频率从886 Hz提高到950 Hz，增大了64 Hz；第四阶固有频率从1 103 Hz 提高到1 575 Hz，提高了472 Hz。分析表明，跟端打磨可在一定程度上提高弹条的固有频率，满足设计需求。

3.3.2 轨距块对弹条模态影响

考虑到轨距块与弹条的直接接触，是钢轨振动传导至弹条的重要途径。为研究轨距块对弹条动力学性能的影响，对不同轨距块阻尼和厚度取值下的弹条分别进行参数化模态分析。分析中，轨距块阻尼系数分别为0.1，0.3，0.5 和1.0，轨距块厚度分别为8，6 和4 mm，计算结果如表8和表9所示。由表8和表9可知：考虑轨距块阻尼时，随着轨距块阻尼系数的增加，弹条的前四阶固有频率略有降低；随着轨距块厚度降低，弹条的前四阶固有频率均有所降低，但变化幅度不大。

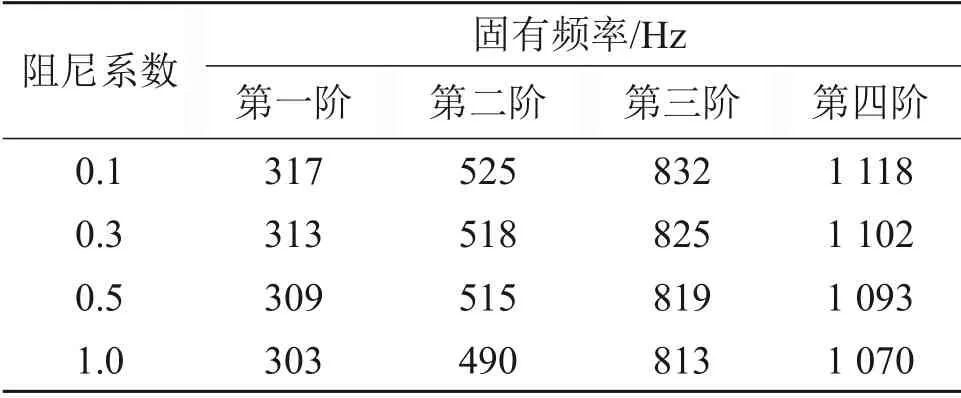
表8 轨距块阻尼对弹条模态的影响Table 8 Influence of gauge block damping on fastener clips mode

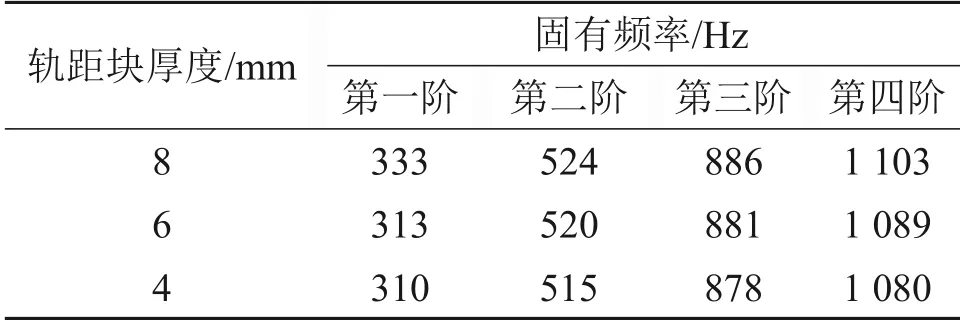
表9 轨距块厚度对弹条模态的影响Table 9 Influence of gauge block thickness on fastener clips mode

4 弹条动态响应分析

4.1 地铁车辆-轨道耦合动力学模型

为了分析不同工况下不同优化措施对弹条动态响应的影响，本文建立地铁车辆-轨道耦合系统动力学模型。借助多体动力学软件SIMPACK和有限元分析软件ANSYS进行联合仿真求解。

车辆-轨道耦合动力学将车辆系统和轨道结构系统看作一个相互作用、相互耦合的整体大系统，把轮轨接触关系作为连接车辆和轨道结构的纽带，在建立车辆-轨道耦合动力学模型时，主要遵循以下基本原则：

1）本文中主要分析车辆和轨道系统的垂向和横向振动响应，故车辆考虑为单节车模型，车体、转向架、轮对和一系、二系悬挂均在模型中予以考虑。

2）采用分层建模思想，地铁轨道模型自上往下依次为钢轨—扣件—轨道板—下部基础体系。

3）轨道结构的支承考虑为弹性离散点支承，可以更好地处理轨道结构参数（如扣件间距、支承弹性和阻尼等）沿轨道纵向不均匀分布的动力学问题。

4）钢轨采用欧拉梁模型，以提高计算精度，减少模型计算时间。

5）轮轨接触考虑为赫兹线性弹簧接触。

6）轨道不平顺采用美国六级谱。

在仿真过程中，轨道模型总长度为150 m，选取50 m 长作为波磨仿真的最大长度，以研究不同波深下的弹条的动力特性。由于深圳地铁11 号线采用的是地铁A 型车，故本模型车辆采用地铁A型车参数，轴距为4.5 m，定距为15.7 m，轴质量为16 t。地铁A 型车的计算参数见表10。表11所示为轨道结构的材料属性参数。

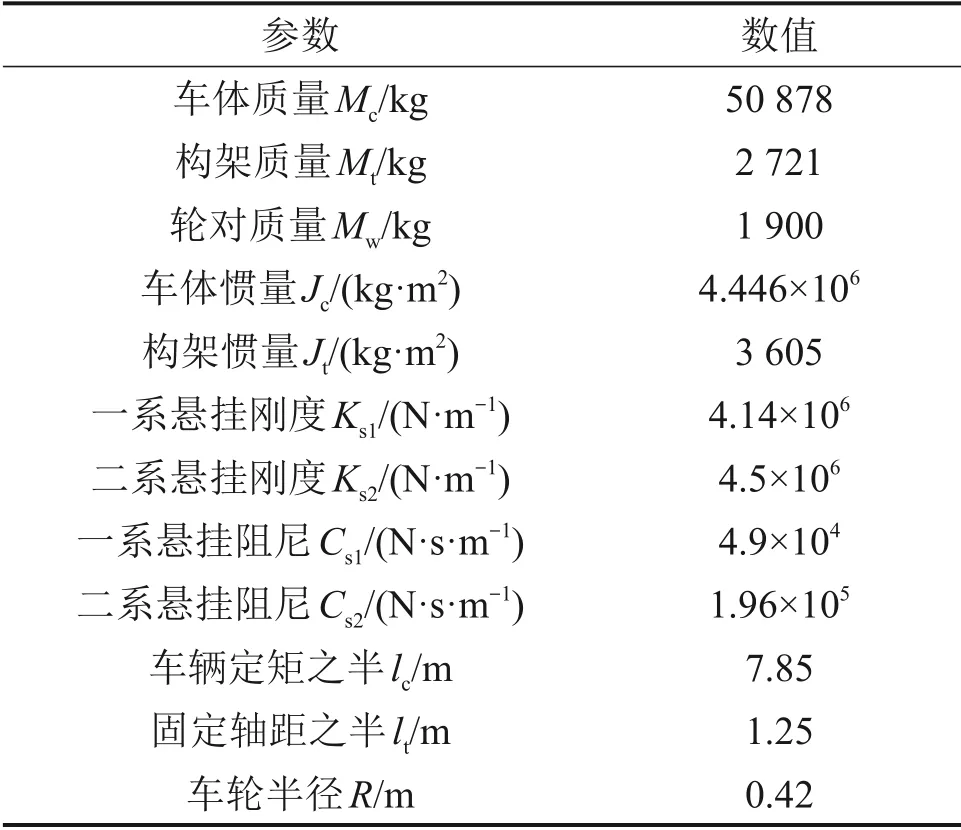
表10 地铁A型车参数Table 10 Metro Type A car parameters

表11 轨道结构参数设置Table 11 Parameters setting in track structure

4.2 弹条动态响应分析

4.2.1 高频弹条动态响应分析

高频弹条的固有频率相对于Ⅲ型弹条得到提高，为探究高频弹条在列车荷载激励下的振动响应，将列车通过时的钢轨动力响应作为扣件系统有限元模型的输入载荷，计算高频弹条动态响应。文献[16]发现Ⅲ型弹条在部分波磨严重段发生大量断裂，经实测后发现，该段存在40 mm 的典型波磨波长。针对这一现象，本文计算钢轨波磨波长为40 mm 和波磨幅值为0.02，0.04，0.06，0.08 和0.10 mm时的高频弹条动态响应，并与普通Ⅲ型弹条进行对比，比较该典型波长下不同波磨幅值对弹条动态响应的影响，如图11所示。

图11 不同波磨幅值下弹条振动加速度Fig.11 Vibration acceleration of fastener clips under different wave amplitudes

从图11可以看出：随着钢轨波磨幅值的增大，高频弹条振动加速度也在增大。当钢轨波磨幅值为0.02 mm 时，Ⅲ型弹条振动加速度最大值为212 m/s2，高频弹条振动加速度最大值为127 m/s2。当钢轨波磨幅值为0.10 mm时，Ⅲ型弹条振动加速度幅值达到1 096 m/s2，高频弹条振动加速度最大值为560 m/s2。在同样波磨情况下，高频弹条相对于Ⅲ型弹条振动加速度明显减弱。

4.2.2 绝缘轨距块阻尼对弹条动态响应分析

绝缘轨距块阻尼能减弱钢轨传递到弹条的振动，当阻尼轨距块阻尼系数为0.3时，计算钢轨波磨波长为40 mm 和波磨幅值为0.02，0.04，0.06，0.08和0.10 mm时的弹条动态响应，并与普通阻尼轨距块对比，如图12所示。

从图12可以看出：随着钢轨波磨幅值增大，弹条振动加速度也在增大。当钢轨波磨幅值为0.02 mm时，正常轨距块下弹条振动加速度最大值为212 m/s2，阻尼轨距块下弹条振动加速度最大值为184 m/s2。当钢轨波磨幅值为0.10 mm 时，正常轨距块下弹条振动加速度最大值为1 096 m/s2，阻尼轨距块下弹条振动加速度最大值为934 m/s2。在同样波磨情况下，采用阻尼轨距块作用时弹条振动加速度略有减弱。

图12 阻尼轨距块下弹条振动加速度Fig.12 Vibration acceleration of fastener clips under damping gauge block

5 弹条疲劳寿命分析

5.1 疲劳分析方法

确定结构疲劳寿命的方法主要有2类：疲劳试验法和疲劳数值模拟法。疲劳试验法通过模拟现场状况获取比较准确的疲劳寿命，成本高；疲劳数值模拟法主要利用计算机进行寿命计算，依据结构材料的疲劳性能，根据结构所受的荷载估算疲劳寿命。结合国内外学者常用的疲劳寿命分析方法[17-19]，本文主要通过基于名义应力法估算弹条的疲劳寿命。弹条受到的载荷属于随机荷载，载荷随时间任意变化，需要采用雨流计数法将荷载谱转换为变幅荷载，再基于Miner线性累积损伤理论计算弹条损伤及疲劳寿命。

为了分析列车通过时弹条的疲劳寿命变化规律，首先，基于有限元理论得到扣件系统服役下弹条的装配应力；然后，将扣件系统的垂向位移时程曲线作为疲劳荷载，分析扣件系统中弹条的受力情况；最后，结合疲劳分析理论和线性累积损伤法则，估算弹条疲劳寿命。

5.2 弹条疲劳分析模型

根据扣件系统中弹条的疲劳应力应变谱，结合疲劳分析理论和累积损伤法则，估算弹条疲劳寿命。扣件弹条采用60Si2Mn 弹簧钢制成，其95%存活率时的σ-N曲线公式为

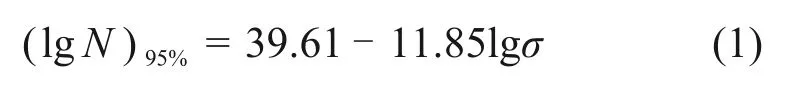
式中：σ为应力循环幅值，MPa；N为试件破坏时应力循环次数。

弹条在安装过程中提供扣压力而产生较大的初始应力，因而仅考虑应力幅值的变化来计算其疲劳寿命是不合理的，应进行平均应力的修正，一般采用工程中应用较多的Goodman 模型[20]进行修正。Goodman公式为

式中：σ-1为应力等于0的疲劳强度，MPa；σu为强度极限，MPa；σm为平均应力，MPa；σa为平均应力等于σm的疲劳强度，MPa。

5.3 扣件弹条疲劳寿命影响因素分析

5.3.1 高频弹条疲劳寿命分析

从前面可以看出：高频弹条固有频率得到提高，有波磨情况下其振动较Ⅲ型弹条的小。本文计算高频弹条在波长40 mm 和波磨幅值为0.02，0.04，0.06，0.08 和0.10 mm 时的弹条应力时程，弹条最大等效应力时程曲线如图13所示。通过雨流计数法得到最大等效应力-时程曲线雨流循环计数幅值分布图，如图14所示。

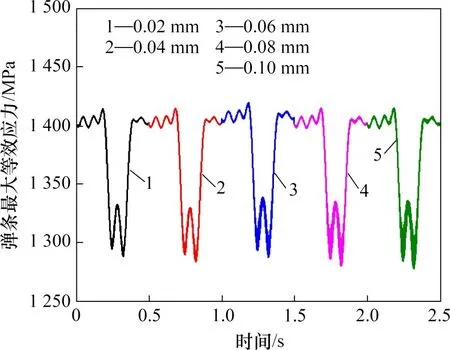
图13 不同波磨幅值下高频弹条最大等效应力时程曲线Fig.13 Time history curves of the maximum equivalent stress of high frequency fastener clips under different amplitudes of wave abrasion

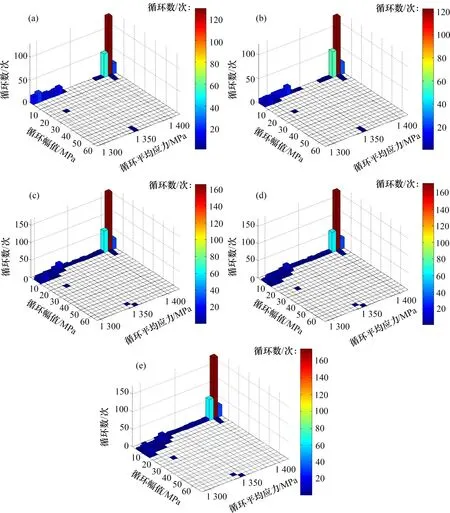
图14 高频弹条在不同波磨幅值下的雨流计数幅值分布Fig.14 Rain flow count amplitude distribution of high-frequency elastic clips under different corrugation amplitudes

根据雨流循环计数以及线性累积算法，可以得到不同波磨幅值下对弹条造成的损伤，如表12所示。从表12可知：波磨幅值越大，对弹条损伤越严重，当波长为40 mm 和波磨幅值为0.10 mm时，轮轨作用对高频弹条的损伤为6.86×10-7，而普通弹条的损伤为4.36×10-6，波磨对高频弹条的损伤相比普通弹条大幅减小。

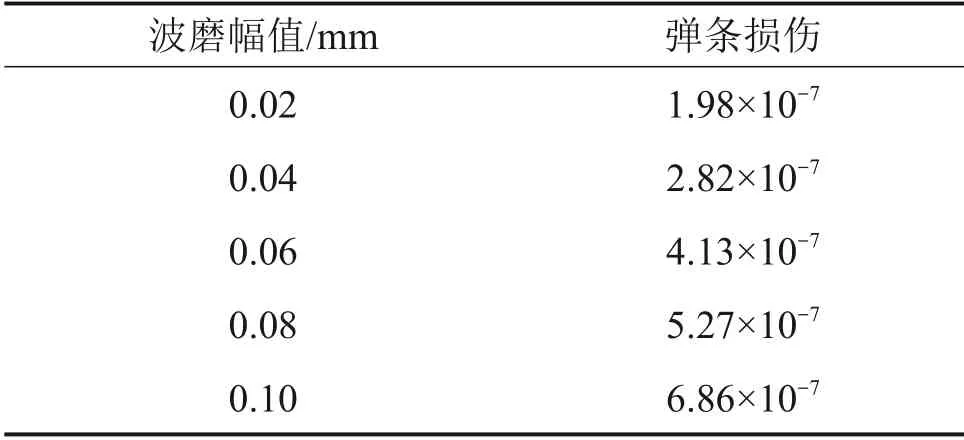
表12 高频弹条在不同波磨幅值下弹条危险点疲劳损伤Table 12 Fatigue damage of dangerous point of highfrequency elastic clips under different corrugation amplitudes

5.3.2 阻尼轨距块对弹条疲劳寿命影响

阻尼轨距块能减小钢轨到弹条的振动，计算弹条在阻尼轨距块下波长为40 mm 和波磨幅值为0.02，0.04，0.06，0.08和0.10 mm时的弹条应力时程，弹条最大等效应力时程曲线如图15所示。通过雨流计数法得到最大等效应力-时程曲线雨流循环计数幅值分布，如图16所示。

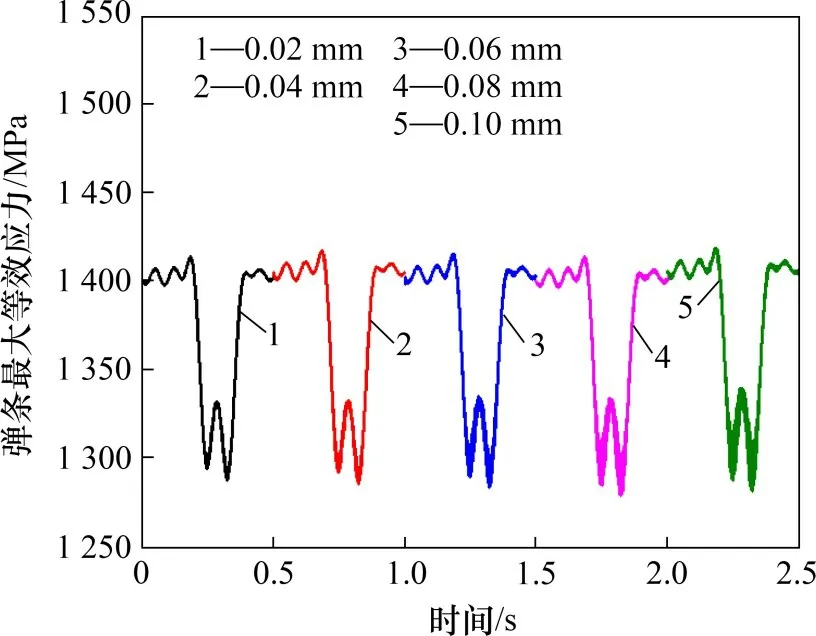
图15 阻尼轨距下弹条最大等效应力时程曲线Fig.15 Time history curves of the maximum equivalent stress of fastener clips under damping gauge

图16 阻尼块下不同波磨幅值时雨流计数幅值分布Fig.16 Amplitude distribution of rain flow count at different corrugation amplitudes under damping block

同样根据雨流循环计数以及线性累积算法，得到不同波磨幅值下弹条造成的损伤如表13所示。从表13可知：波磨幅值越大，对弹条损伤越严重；当波长为40 mm和波磨幅值为0.10 mm时，有阻尼轨距块时轮轨作用对弹条的损伤为1.12×10-6，正常轨距块普通弹条的损伤为4.36×10-6，使用阻尼轨距块时弹条损伤相比正常轨距块时有一定程度减小。

表13 阻尼块下不同波磨幅值时弹条危险点疲劳损伤Table 13 Fatigue damage of dangerous points of spring bar at different corrugation amplitudes under damping block

6 结论

1）Ⅲ型高频弹条最大等效应力为1 400 MPa，扣压力为11.7 kN，与原Ⅲ型弹条相比，其最大等效应力及扣压力基本无变化，而最大等效应力的位置由后拱小圆弧与中肢连接处转移到后拱小圆弧靠近跟端处。

2）与Ⅲ型弹条相比，Ⅲ型高频弹条的前四阶固有频率均有所提高。其中，弹条的第一阶固有频率从333 Hz 提高到358 Hz；第二阶固有频率从524 Hz 提高到690 Hz；第三阶固有频率从886 Hz提高到950 Hz；第四阶固有频率从1 103 Hz 提高到1 575 Hz。分析表明跟端打磨可有效地提高弹条的固有频率。

3）考虑轨距块阻尼时，弹条的前四阶固有频率与不考虑轨距块阻尼相比变化不大，且随着轨距块阻尼系数的增加，弹条的固有频率略有降低。阻尼轨距块能在一定频段内减小钢轨传递到弹条趾端的振动。

4）当钢轨波磨波长为40 mm和幅值为0.10 mm时，Ⅲ型弹条振动加速度幅值达到1 096 m/s2，高频弹条振动加速度最大值为560 m/s2。在有波磨情况下，高频弹条相对于Ⅲ型弹条振动加速度明显减弱。高频弹条的损伤为6.86×10-7，普通弹条的损伤为4.36×10-6，波磨对高频弹条的损伤相比普通弹条大幅减小。

5）当钢轨波磨波长为40 mm和幅值为0.10 mm时，正常轨距块下弹条振动加速度最大值为1 095 m/s2，阻尼轨距块下弹条振动加速度最大值为934 m/s2。在阻尼轨距块作用下，弹条振动加速度得到减弱。有阻尼轨距块时轮轨作用对弹条的损伤为1.12×10-6，正常轨距块时弹条损伤为4.36×10-6，使用阻尼轨距块时弹条损伤相比正常轨距块时略有降低。