碳纤维增强透声型浮力材料夹层板弯曲刚度特性
2021-11-25付晓梅志远张二陈国涛祝熠
付晓,梅志远,张二,陈国涛,祝熠
(海军工程大学舰船与海洋学院,湖北武汉,430033)
舰艇声呐导流罩是确保声呐平台正常工作,充分发挥声呐观测潜力的重要平台。舰艇首部声呐导流罩承受水动力载荷及偶发性突加载荷,为满足导流罩壳体结构的刚度和强度要求,需具有一定的强度刚度以保证舰艇型线光顺,同时,由于声呐的存在,又需要其具备优良的透声性能。对传统声呐导流罩壳板而言,壳板厚度与材料的透声性能对导流罩整体性能具有重要影响。降低壳板厚度必然会极大地改善透声性能,然而,壳板过薄则难以保证强度刚度要求。采用复合材料夹层板较好地解决了此类问题,纤维增强复合材料夹层薄板结构被认为是未来发展的一种趋势[1]。碳纤维是一种高强度、高模量的新型纤维材料,兼具碳材料和纤维材料的双重优良特性,其质量比钢、镁、铝质量低,但强度、模量却很高,是典型的高强度轻量化材料,较铝合金及钢材有着良好的材料力学性能[2]。结合材料的透声特性与性能参数[3],选用高透声性低密度材料作为芯材,高模高强材料作为表层的复合材料夹层板具有高强度刚度、高透声性能的优势,可较好地满足导流罩工作环境的要求。
针对复合材料壳板的声学性能研究,目前多涉及壳板吸声、隔声问题,有关透声性能的优化研究较少。在国外,KURTZE等[4]较早开始了夹层板的传声损失研究,并且考虑了3种形式的动力学状态用以确定理想夹层板的声学行为;PAOLOZZI等[5-6]研究了夹层板固有频率对传声特性的影响,并对芯层刚度进行了优化;MOORE 等[7]对具有均质和正交各向异性夹芯的对称无限大夹层复合材料板的声传递特性进行了研究;PATIL[8]用统计能量法对具有均质芯层和正交各向异性蜂窝芯层的有限尺寸夹层结构复合材料板的传声损失进行了估计。国内对夹层板声学性能的研究相对较晚,黄文超[9]于1990年将蜂窝夹层结构应用于螺旋桨飞机的座舱降噪中,研究了蜂窝夹层结构的声透射机理;王志瑾等[10]针对皱褶夹芯形式的蜂窝夹层结构进行了隔声性能的机理研究,得到了各频率段影响其隔声特性的主要参数变化规律。
针对复合材料夹层板的刚度优化问题,国内外学者进行了许多研究[11-18]。钟焕杰[12]借助拓扑优化完成了对薄壁加筋结构的优化设计;赵群等[15-16]研究了加筋板刚度匹配下的失稳变形模态,同时提出了一种以压缩、弯曲刚度系数作为设计变量的模型设计方法;李林远等[17]基于无网格法和遗传算法,对矩形加肋板肋条位置进行了优化;熊长丽[18]使用碳纤维材料代替金属材料,实现了汽车B柱等刚度条件下的轻量化设计,但上述研究对象多为加筋板结构,较少涉及夹层板格的刚度优化问题,对于壳板透声性能与力学性能交互的优化设计研究也较少。然而,透声型复合材料夹层板在导流罩、雷达罩等对透声性能要求高的结构中具有非常重要的作用,在对该类结构优化设计时考虑透声特性,将会极大提升结构整体性能。
结合夹层板研究现状,本文作者提出碳纤维增强透声型浮力材料夹层板方案,通过层合板弯曲理论推导夹层板结构弯曲刚度系数,并探讨高模量高强度材料与低模量功能型材料对所构成夹层板弯曲刚度的贡献率,进而研究夹层平板的刚度特性变化规律。
1 透声型夹层板弯曲刚度变化规律
1.1 理论分析
夹层结构通常由较薄的面板与较厚的芯材组成,而层合板由单层板按规定的纤维方向和次序铺放成叠层形式,进行黏合、加热固化而成。相比较而言,夹层板与夹层混杂层合板具有相似之处,结合本文提出的夹层板方案,可认为夹层板是由上下两层层合板以及中间的均质芯材组成。本文根据经典层合板理论,首先从层合板的弯曲刚度表达式开始探讨,验证此公式是否可以推广至夹层板结构,用以评价夹层板的弯曲刚度。
假设夹层混杂层合板表层和芯材2种材料的工程常数分别为:表层材料,1方向弹性模量E1,a和2方向弹性模量E2,a以及泊松比μ12,a;芯材,1方向弹性模量E1,b和2 方向弹性模量E2,b以及泊松比μ12,b。对于正交各向异性层合板,由于织物采用0°/90°正交铺层,其工程常数E11=E22,则有退缩刚度系数Q11=Q22,层合板厚度为h,其中表层材料总厚度为ha,芯材的总厚度为hb;定义混杂比图1所示为正交对称铺层的夹层混杂层合板。

图1 夹层混杂层合板Fig.1 Sandwich hybrid laminate
由经典层合板理论[19],层合板的刚度表达式为
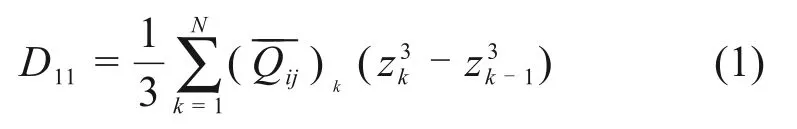
式中:N为层数;()k为第k层材料的退缩刚度系数;zk为第k层铺层的下表面的坐标(板中面为坐标原点,向上为正)。
将图1所示的夹层板各部分结果代入式(1),化简合并后,可得其弯曲刚度系数的计算公式为

由于μ12,a·μ21,a≪1;μ12,b·μ21,b≪1,对D11的影响极小,可将其省略,并令E1,a=kE1,b,简化为
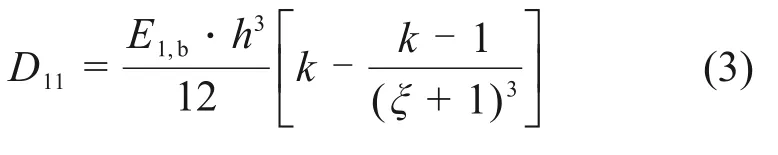
假设夹层板由上下两块层合板与芯材组成的结构,最终其刚度计算公式即为表层与芯材的弯曲刚度相加,夹层板的弯曲刚度见式(4),弯曲刚度除以单位长度后即可得到该结构的弯曲刚度系数。
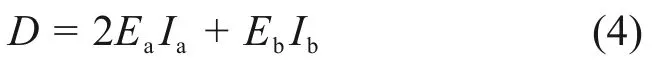
式中:Ea和Eb分别为表层和芯材的弹性模量;Ia和Ib分别为表层或芯材对夹层板中性轴的弯曲惯性矩。
任取一夹层平板(表层为厚度2.48 mm 的碳纤维材料,芯材为厚度16 mm 的浮力材料),分别根据式(3)与式(4)计算夹层板的弯曲刚度系数,如表1所示。由表1可知:2 种理论所计算的弯曲刚度系数相对误差较小,说明式(3)和式(4)均可以用于评价夹层板的刚度。

表1 采用2种公式计算的夹层板刚度系数Table 1 Stiffness coefficient of sandwich plate calculated by two formulas
1.2 透声型碳纤维夹层板刚度影响因素分析
透声型浮力材料具备低密度、高透声的显著特点,在具备透声功能结构中得到广泛使用。本文采用课题组自研浮力材料,在树脂中预加入真空微珠(微珠需提前预制),充分搅拌,以达到降低密度、提高透声性能的目的,同时保证材料具有较高的强度。图2所示为该结构制作原理。

图2 浮力材料制作原理示意图Fig.2 Schematic diagram of buoyant material
该材料在透声性能方面表现优异,厚度为20 mm 的浮力材料透声系数可达0.99[3],其透声系数的拟合曲线如图3所示。该材料应用在夹层平板中能够改善整体的透声性能,但是其自身性能参数难以满足结构承载要求,又需要增大其他材料强度以保证夹层板基本的力学性能,因此,本文提出的碳纤维增强浮力材料夹层板具有可行性。表2所示为本文所用透声型浮力材料的力学性能参数。

表2 材料性能参数Table 2 Material performance parameters
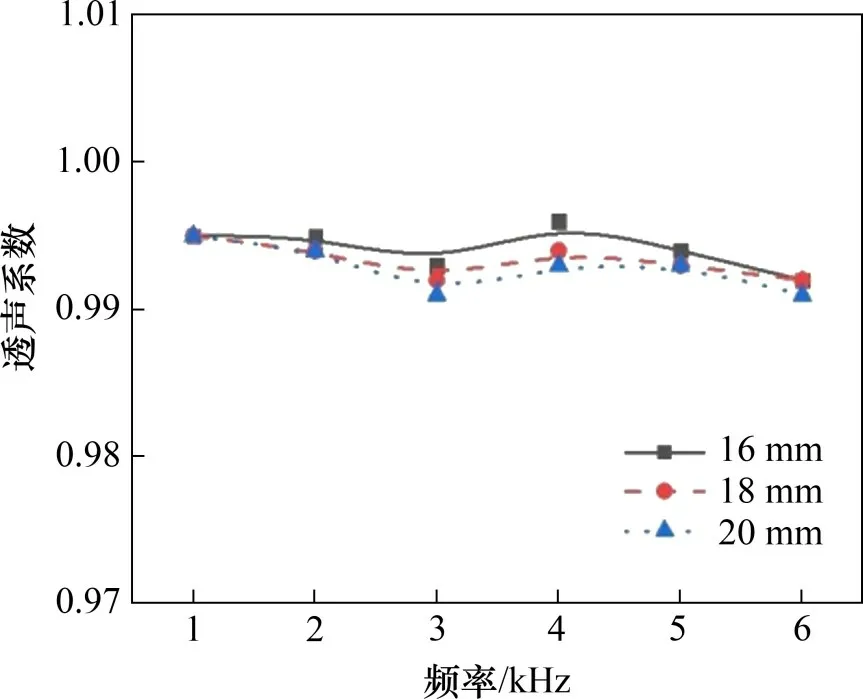
图3 透声型浮力材料的透声系数拟合曲线Fig.3 Fitting curve of sound transmission coefficient of transparent buoyancy material
根据1.1节中的理论推导,探讨夹层板表层与芯材对整体弯曲刚度的贡献率,定义表层碳纤维弯曲刚度D1与芯材弯曲刚度D2之比为β,其表达式如下:
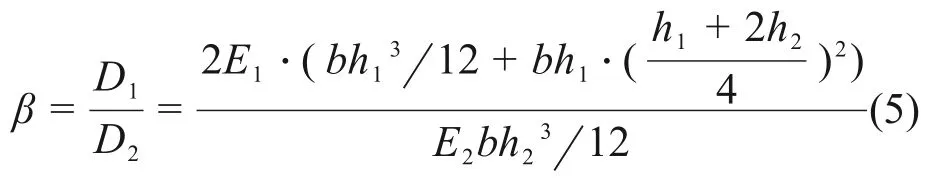
记E1=E2,h1/h2=ξ,则式(5)可化简为
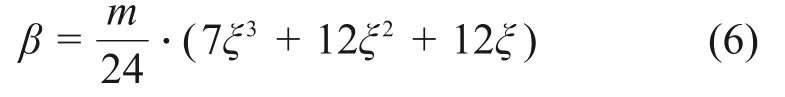
结合工程实际,夹层板混杂比ξ一般在0~100%之间,由此可见β一般远大于1,以常见碳纤维材料的弹性模量60 GPa代入计算,当ξ=10%时,β=2.76,表层材料对整体刚度贡献率为73.4%。即对夹层板而言,表层碳纤维材料对整体刚度的贡献明显比透声型浮力芯材的高,浮力材料主要起透声与减小质量的作用,对夹层板弯曲刚度的影响程度有限。因此,在夹层板刚度优化分析时,需要着重关注表层碳纤维材料对弯曲刚度的影响。
1.3 基于数值计算的夹层板弯曲刚度特性规律分析
结合1.1节中的理论推导,本文通过ABAQUS软件,对夹层板表层及芯材厚度对刚度的影响情况进行仿真分析,图4所示为模型示意图。依据工程背景需求,取长×宽为3m×2 m的矩形板格,板格表层为碳纤维材料(T700/350),芯材为透声型浮力材料,使用实体单元建模,采用线性分析步,施加均布载荷。边界条件为四周固支,表层碳纤维区域网格单元为SC8R,其余区域网格单元为C3D8R,网格尺寸为10 mm,芯材厚度为8~20 mm,表层厚度为0.64~5.58 mm,绘制不同芯材厚度时夹层板最大位移随表层厚度变化曲线,如图5所示。
图4 有限元仿真模型图Fig.4 Finite element simulation model
由图5可见:夹层板的位移能够直观地反映其刚度水平(位移越大,板的刚度越小),显然,表层厚度对夹层板位移的影响较为显著,此结论与前文推导的结论一致。当表层厚度一定时,随着芯材厚度增加,夹层板模型刚度逐渐增加,但当芯材厚度为16 mm 时,其对弯曲刚度影响程度明显降低;当芯材厚度一定时,随着表层厚度增加,夹层壳板刚度逐渐增加,但其影响程度也随之降低,主要表现为每条曲线在表层厚度达到一定时,不同芯材厚度的表层厚度-位移曲线均存在拐点即优化效率最优点,该位置过后表层厚度增加对壳板刚度影响明显下降。对于本文所取板格,即对芯材厚度为16 mm时曲线通过拟合可得其表层厚度与刚度的函数关系即式(7),然后对该函数进行解析,求解可知当横坐标为2.5 mm 时,优化效率达到最优点。

图5 表层厚度-位移曲线Fig.5 Thickness-displacement curves of surface layer

2 透声型碳纤维夹层板力学性能试验研究
2.1 夹层板的制备
在复合材料结构工程应用中,常见的纤维有碳纤维、玻璃纤维、芳纶纤维等,其中T700 与其他牌号碳纤维相比具有如下优点:单向布具有较高的强度和模量;密度(1.43 g/cm3)低于玻璃纤维布密度(1.76 g/cm3);T700 碳纤维布与环氧树脂成型界面浸润性能比乙烯基树脂的优。此外,T700/350具有良好的透声性能,可较好地适用于透声性能要求下的结构设计中。因此,本文进行力学性能试验所用夹层板的材料体系如下:树脂基体材料为QC-350 环氧树脂,纤维增强体为T700 单向布(0.31 mm/层),芯材为自研透声浮力材料。
碳纤维夹层板的制作采取真空成型工艺制作,使用QC-350 环氧树脂粘接上、下蒙皮与芯层,形成“蒙皮—芯层—蒙皮”的三层结构,板的上下表层碳纤维铺层顺序为(0°/90°)4,织物正交铺层,厚度为2.48 mm,夹芯透声材料厚度为16 mm,夹层板总厚度为20.96 mm,图6和图7所示分别为夹层板具体尺寸示意图及剖面图。
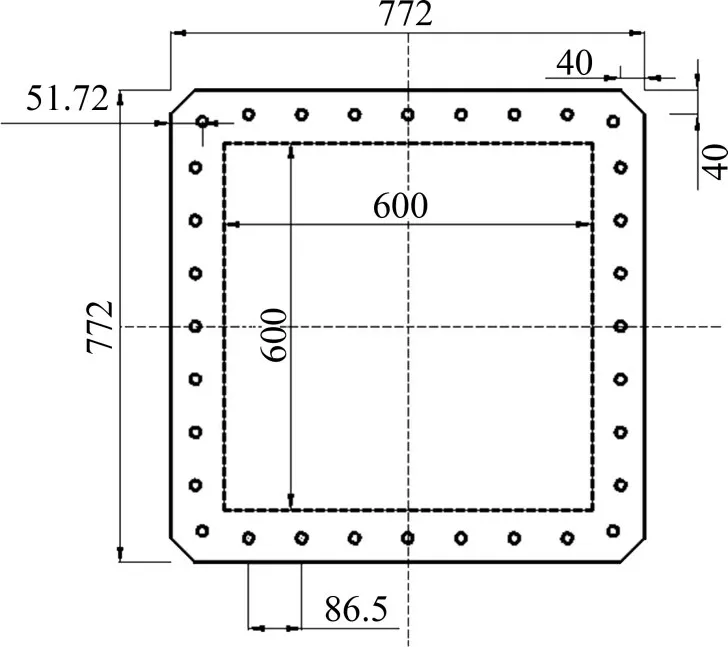
图6 碳纤维夹层板尺寸示意图Fig.6 Dimensions of carbon fiber sandwich plate

图7 碳纤维夹层板剖面图Fig.7 Section of carbon fiber sandwich plate
2.2 夹层板仿真分析
试验开始前,通过ABAQUS 软件,对夹层板进行有限元仿真计算,初步了解其强度、刚度,为确定试验方案、选取测点等方面提供指导。模型采用实体单元建模,使用线性分析步,在试验区施加均布载荷,边界条件四周固支,表层碳纤维区域网格单元为SC8R,其余区域网格单元为C3D8R,网格尺寸为20 mm,图8所示为碳纤维夹层板有限元计算模型。
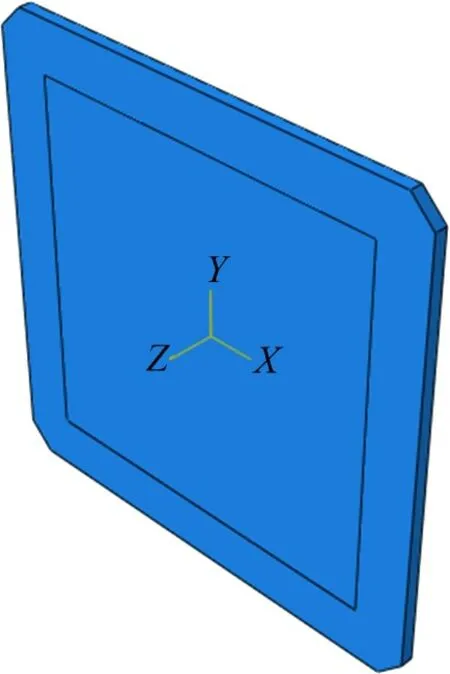
图8 碳纤维夹层板有限元计算模型Fig.8 Finite element calculation model of carbon fiber sandwich plate
2.3 碳纤维夹层板强度刚度试验
为测试本文提出的碳纤维夹层板是否满足规范要求,同时验证本文仿真方法的准确性。本文开展碳纤维夹层板模型试验,采用正、负压稳压试验方法。模型工装与夹层板组成密闭空间,利用空压机向工装模型内加压以达到正压状态,利用真空泵对工装模型进行抽真空以达到负压状态,图9所示为试验框图。
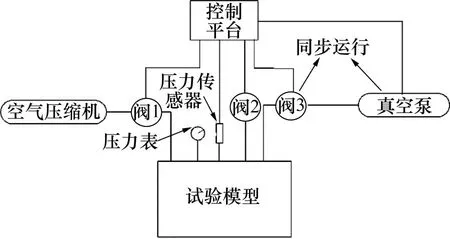
图9 试验框图Fig.9 Test block diagram
试验流程为:试验前先进行1~2 次静压试验,消除残余应力。首先进行正压试验,启动空压机,向模型内部充气,直至到达设定的载荷,压力传感器反馈信号至控制平台,将阀门1关闭,待压力传感器示数稳定,记录各通道数据。然后打开控制阀1,向模型内部充气至下一设定载荷,以此类推,直至载荷增加至试验设定的最大值,正压试验完成。打开控制阀2,将模型内的气体释放至大气中,当模型内部压力降至与大气压相同时,关闭控制阀2,准备进行负压试验。打开控制阀3,开启真空泵,抽取模型内部气体至设定载荷,此时,压力传感器反馈信号至控制平台,关闭真空泵与控制阀3,待压力传感器示数稳定,记录各通道结果。然后继续抽取模型内部气体达到下一载荷,以此类推,当载荷增加至设定的最大值后,完成负压试验。最后打开控制阀2,使模型内部气压恢复至标准大气压,关闭控制阀2。重复上述过程3次,记录相关数据,试验完成。
在试验开始前,根据2.2 节中有限元分析结果,分别选取具有代表性的5 个位移和应变测点,图10和图11所示分别为具体测点布置方案。
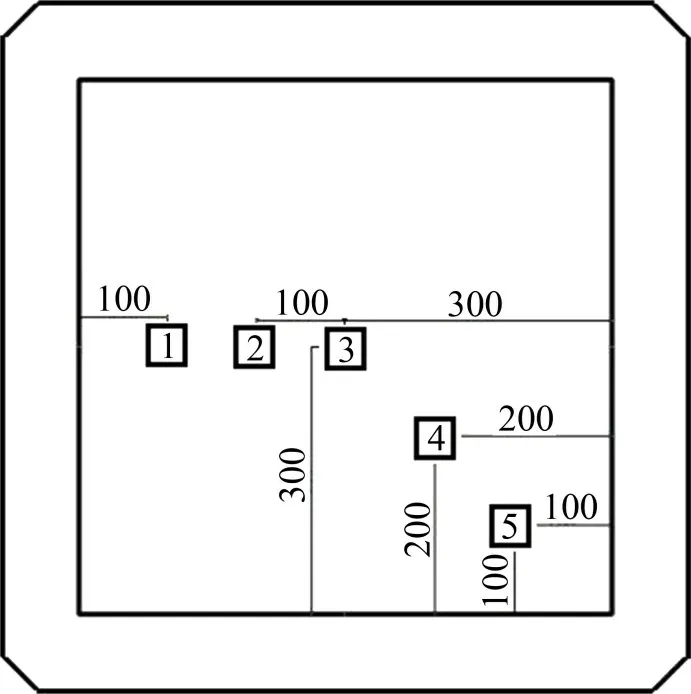
图10 刚度试验位移计测点布置Fig.10 Layout of measuring points of stiffness test
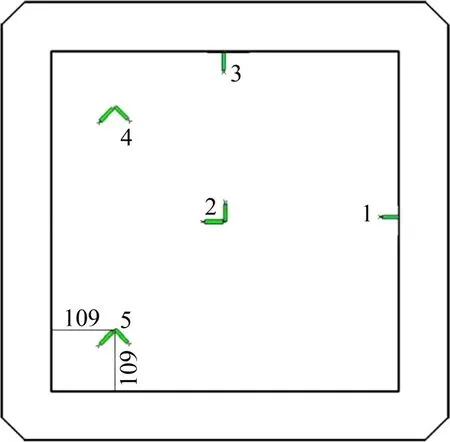
图11 强度试验应变测点及布置Fig.11 Strain measuring points and layout of strength test
2.4 试验结果分析
根据2.3节测点布置方案,分别在模型上读取各测点的仿真计算数据,然后与各测点的试验值进行对比分析,验证仿真方法的准确性。表3和表4所示分别为碳纤维夹层板承受50 kPa均布载荷时应变和位移测点的试验值与仿真值结果。
由表3可知:夹层板的各应变测点试验值与仿真值数据拟合较好,相对误差较小,均在可接受范围内,说明本文仿真方法在应变分析上的可信度较高。
由表4可知:除5号位移测点外,夹层板的各应变测点试验值与仿真值数据拟合较好,相对误差较小,均在可接受范围内。对于5 号位移测点,由于其位置距离边界较近,受边界影响较大,且在试验中边界条件很难达到理想的固支状态,同时该点位移较小,仪器的测量误差对其影响较大。综合比较各测点位移,说明本文仿真方法在位移分析上具有较高的可信度。由表3和表4可知:本文仿真方法的准确性较高,说明夹层板刚度特性变化规律应用于工程设计具有可行性。
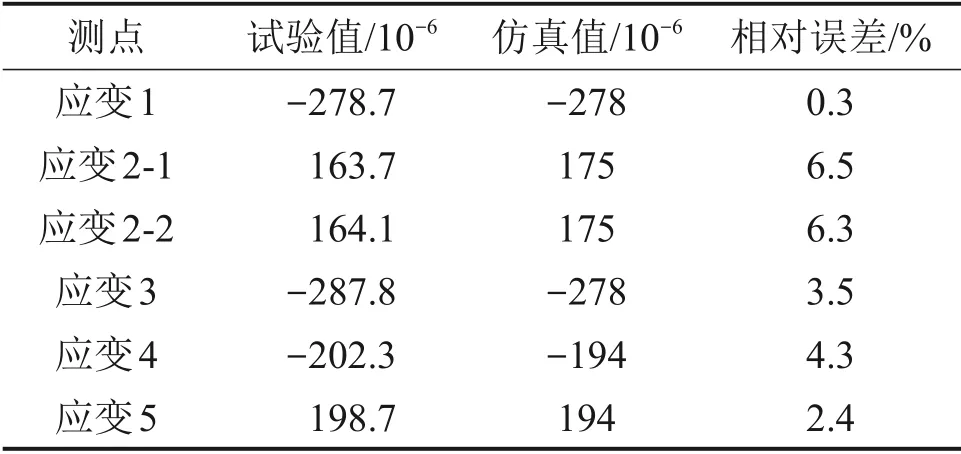
表3 夹层板应变测点试验值与仿真值Table 3 Test value and simulation value of strain measuring point of sandwich plate
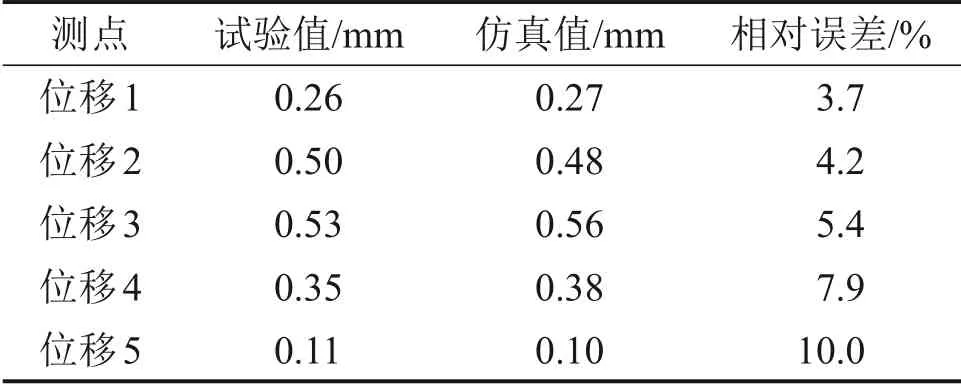
表4 夹层板位移测点试验值与仿真值Table 4 Test value and simulation value of displacement measuring point of sandwich plate
3 结论
1)本文将层合板的弯曲刚度系数公式与材料力学截面弯曲刚度计算公式联系起来。经对比分析,证明2种公式均可用于夹层板弯曲刚度计算。
2)由夹层板表层与芯材的弯曲刚度比表达式可知,本文所使用的透声型浮力材料作为芯材对整体刚度贡献率较低,夹层板弯曲刚度主要受表层材料属性及厚度的影响,在优化设计时需重点关注。
3)夹层板刚度优化中普遍存在效率最优点,在此之后,增加表层厚度对整体刚度的作用明显下降,但是其刚度维持在较高值。在夹层板优化设计中,参考弯曲刚度特性变化规律有利于提高优化效率。
4)对于夹层板优化设计,选择具备高强度材料作为表层,其他功能型材料作为芯材,能够较好地兼顾结构功能与力学性能的需求。本文通过理论和数值分析,探讨了夹层板弯曲刚度规律并通过试验加以验证,可为夹层板的工程应用提供借鉴。
