基于短时傅里叶变换和时域包络的AEB系统预警声信号时间提取方法*

杨刚 杨小青 钟欣

（1.重庆车辆检测研究院有限公司 国家客车质量监督检验中心，重庆 401122；2.汽车主动安全测试技术重庆市工业和信息化重点实验室，重庆 401122；3.重庆大学，重庆 400030）

主题词：自动紧急制动系统 主动安全 包络提取 短时傅里叶变换

1 前言

自动紧急制动（Automatic Emergency Braking，AEB）系统是避免碰撞事故发生的重要主动安全系统[1-3]，已成为主动安全领域研究的热点。

AEB 系统的控制策略和测试验证对系统优化起着至关重要的作用，国内外学者对此进行了深入的研究。兰凤崇等[4]提出一种考虑预碰撞时间的AEB 系统分层控制策略，在考虑舒适性的条件下确定预碰撞时间阈值。高振海等[5]基于地面目标运动状态转移机理提出了一种基于时间窗的汽车前方静、动态目标状态分类方法。杨为等[6]提出了一种采用上层模糊控制和下层PID控制的分层控制行人避撞策略。季中豪等[7]基于对实车自动紧急制动和前向碰撞预警功能的测试数据，研究了AEB系统的测试评价方法。郭建英等[8]提出了一套AEB系统核心控制策略，完成了对车辆AEB系统性能的道路验证测试。但以上分析和测试验证都仅基于控制策略的控制信号，或者直接从车辆CAN总线采集预警信号，忽略了实际测试过程中预警声音信号的准确性。预警声音会提醒驾驶员采取措施以降低事故发生的概率，而预警声音需要在合适的时间发出[9]。目前，AEB 系统测试中普遍采用麦克风采集预警声音，需要准确计算预警开始时刻，否则会直接影响测试结果的判定。

鉴于上述因素，本文提出一种基于短时傅里叶变换（Short-Time Fourier Transform，STFT）和信号包络的AEB 系统测试预警时间提取方法。分别从频域和时域计算低噪声情况下预警发生时间和两者之间的差值，再利用STFT 提取实际高噪声预警信号中的预警发生时间，采用低噪声情况下的时间差值校正预警发生时间，从而获得准确的预警时间，并开展仿真与试验，验证方法的准确性。

2 预警时间提取原理

车辆在进行AEB 系统道路试验时，麦克风采集的预警声音往往包括一些外界的噪声，以致难以从高噪声的预警声音中获取准确的预警时间。因此，本文提出一种结合STFT和希尔伯特（Hilbert）包络的预警时间提取方法，原理如图1所示，主要包括时、频域法获取低噪声预警时间差和准确提取高噪声信号预警时间2个步骤。

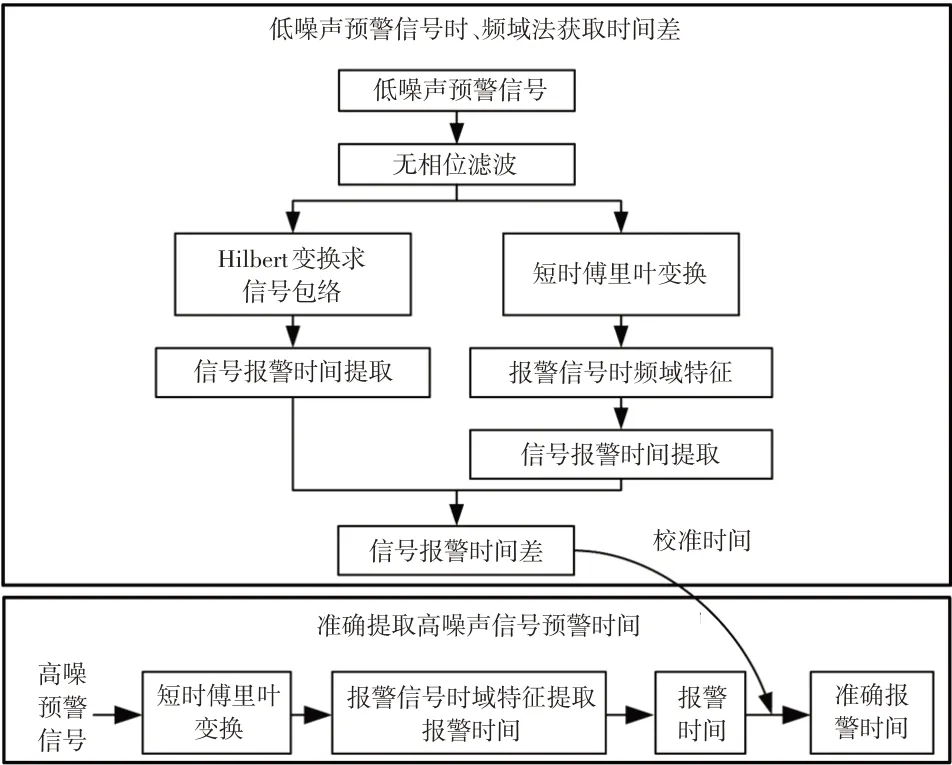
图1 预警时间准确提取原理

2.1 时、频域法获取低噪声预警时间差

为准确提取实际声信号的报警时间，先通过时、频域法获取低噪声预警信号时间差，步骤如下：

a.对低噪声预警信号进行无相位带通滤波。无相位带通滤波器的上、下截止频率根据车辆发出的预警声音频率确定，滤波后得到降噪后的信号x(t)。

b.从时域获取预警时间。对x(t)进行Hilbert 变换[10]，其表达式为：

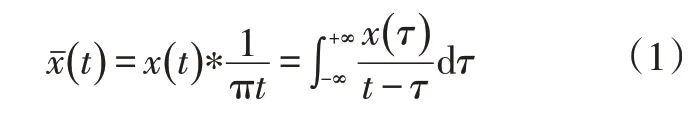
式中，*表示卷积运算；τ为积分变量；t为采样时间。

x(t)进行Hilbert变换后得到信号包络A(t)为：

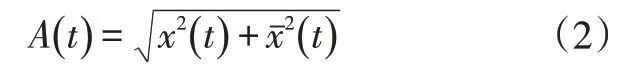
低噪声预警信号是在外界较安静的环境下采集的声音，可直接对滤波后的信号进行Hilbert 变换求信号包络，再对包络求差分得到低噪预警信号中预警的准确开始和结束时间。

c.从频域获取预警时间。对滤波后的低噪声预警信号x(t)进行短时傅里叶变换，得到时频域特征，其表达式为[11]：

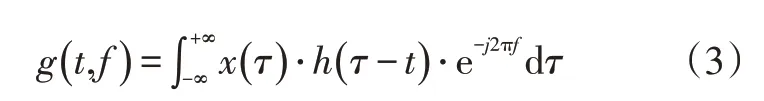
式中，h(t)为窗函数；g(t,f)为关于时间t和频率f的函数。

预警信号经过短时傅里叶变换后，从信号的时频图可得到预警信号的最大幅值Am及其对应的频率fm。分别设定幅值和频率范围为[Am-Ae,Am+Ae]和[fm-fe,fm+fe]，其中Ae为幅值宽度，一般设定为0.3Am～0.8Am，fe为频率宽度，一般设定为1～3个频率分辨率。

在短时傅里叶变换运算中，每个窗长的信号经傅里叶变换后，如果每一小段频谱中最大幅值及其对应的频率同时满足设定的幅值和频率范围，将该时刻的结果设定为1，反之，该时刻的结果设定为0。其中1表示该时刻识别到预警信号，0则表示该时刻没有识别到预警信号。

d.计算时域和频域法获取的预警时间的差值。低噪声预警信号经过短时傅里叶变换计算得到的预警时间受到中心频率的幅值宽度和频带宽度影响，计算结果不准确。而低噪声预警信号通过Hilbert 求时域包络得到的预警时间是准确的，计算时域和频域法获取预警时间的差值tm。

2.2 准确提取高噪声信号预警时间

AEB 系统测试得到的预警声信号一般含有较多噪声，Hilbert 求时域包络会受到外界噪声的影响，无法得到高噪声信号的准确预警时间，而短时傅里叶变换计算的预警时间受中心频率幅值宽度和频带宽度的影响也存在误差，但该误差与短时傅里叶变换计算低噪声信号的预警时间误差tm相同。所以，先对高噪声预警信号进行短时傅里叶变换计算预警时间，再对预警开始和结束时刻进行校正，得到准确的预警过程。

3 仿真计算与分析

3.1 低噪声预警仿真信号

3.1.1 低噪声预警信号仿真模型

构造模拟实际预警声信号的调幅信号y(t)：

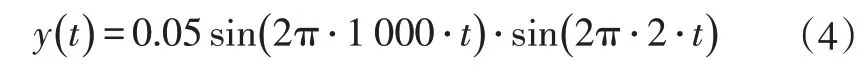
由式（4）可知，y(t)是载波频率为1 000 Hz，调制频率为2 Hz 的调幅信号。为了模拟实际声音信号，取y(t)信号的前半个周期，即0.25 s的信号作为y(t)。z(t)为一个5 s 的信号，分别在第0.5 s、第1.5 s、第2.5 s、第3.5 s、第4.5 s 处发出预警声音信号y(t)，并在信号z(t)中加入30 dB的高斯白噪声，z(t)信号的时域图如图2所示，时频图如图3所示，其中采样频率fs=20 kHz。

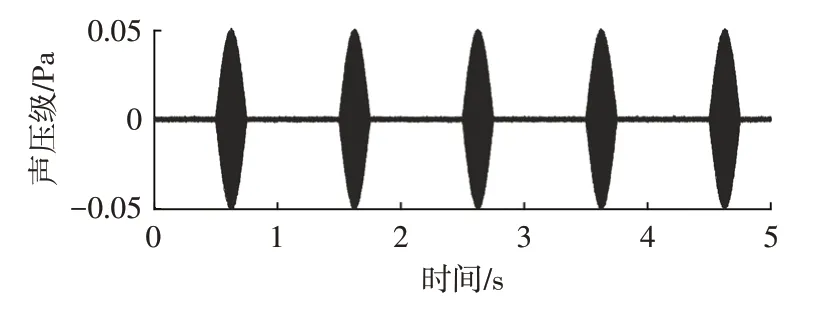
图2 z(t)信号时域图

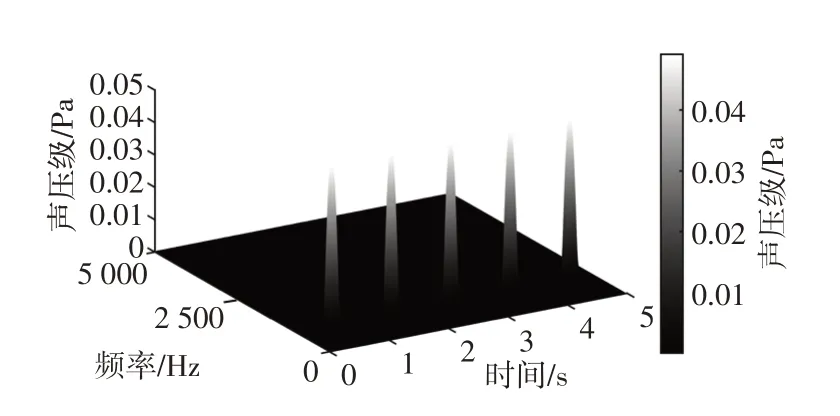
图3 z(t)信号时频图

3.1.2 时域法获取预警时间

时域信号除白噪声外无明显的干扰噪声，可将信号直接进行Hilbert 变换求包络来识别预警时间。从频域特征可知预警声的频率为1 000 Hz，所以将z(t)信号进行无相位带通滤波，通带范围为[950,1 050] Hz，阶数为200阶。滤波后的信号根据Hilbert变换求得包络如图4所示。从图4中可知，第1个预警声信号的开始时刻为第0.499 7 s，结束时刻为第0.752 8 s，与仿真中设置的第0.50 s和第0.75 s相比误差极小。

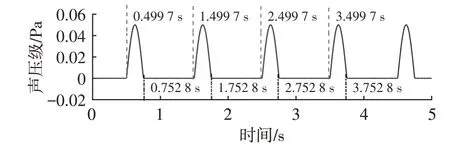
图4 z(t)信号包络

3.1.3 频域法获取预警时间

将z(t)信号进行无相位带通滤波后进行短时傅里叶变换，窗长选用1 000个数据点，选取汉宁窗，重叠率为90%，对应的频率分辨率为20 Hz，时频图见图3，信号的最大幅值为0.05 Pa，为了识别到声音并同时降低噪声信号的干扰，设Ae=0.02 Pa，最大幅值识别范围为[0.03,0.07]Pa。最大幅值对应的频率为1 000 Hz，为了识别到声音并考虑短时傅里叶变换的频率分辨率为20 Hz，设fe=20 Hz，最大幅值对应的频率范围为[980,1 020]Hz。

如果信号最大幅值对应的频率在[980,1 020]Hz 范围内且最大幅值在[0.03,0.07]Pa范围内，说明满足频域特征，将该时刻的结果设定为1，反之，该时刻的结果设定为0，设求得的结果为)，信号预警时刻如图5所示。计算可得第1 个预警声信号的开始时刻为第0.555 s，结束时刻为第0.700 s，误差与实际的开始时刻第0.5 s 和结束时刻第0.75 s 相差较大。误差产生的原因是信号在进行短时傅里叶变换计算时窗长是移动的，当移动窗内有效数据的数量较少时，傅里叶变换计算的幅值就会较小，不在设定的最大幅值范围内，但是设置幅值宽度太大会造成外界干扰触发预警。

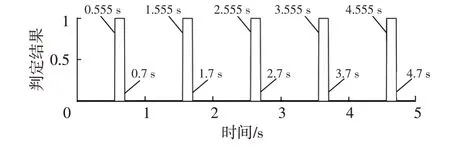
图5 信号预警时刻

3.1.4 低噪声信号时域和频域法时间差

为了消除频域法因幅值宽度大造成的时间差，对频域法计算的预警时刻进行修正。将信号求差分，找到求差分后等于1和-1的所有点，将图5中求差分计算值等于1 的所有数据点对应的时刻向左移动(0.555 0-0.499 7)s=0.055 3 s，将等于-1 的数据点对应的时刻向右移动(0.752 8-0.700 0)s=0.052 8 s。用校准的方法重新计算z(t)预警时刻，计算结果如图6所示，此时计算的结果和仿真结果相比几乎无误差。

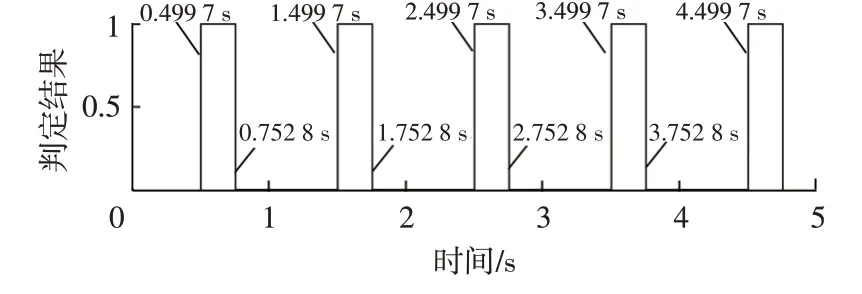
图6 低噪声预警时刻校正

3.2 高噪声信号预警时间的获取

3.2.1 高噪声信号仿真模型

为了考察所提出方法识别预警信号并模拟实际声信号的效果，在仿真信号中先加入噪声u(t)，其表达式为：

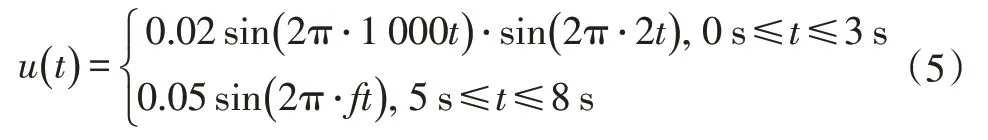
式中，f=400t-800。

仿真实际预警声音信号，取y(t)信号的前半个周期0.25 s 的信号作为y(t) 。分别在信号u(t)的第1 s、第2 s、第3 s、第4 s 处发出预警信号y(t)，并在信号中加入30 dB 的高斯白噪声，所得信号的时域图如图7 所示，时频图如图8所示，其中采样频率fs=20 kHz，窗长选用1 000个数据点，选取汉宁窗，重叠率为90%。

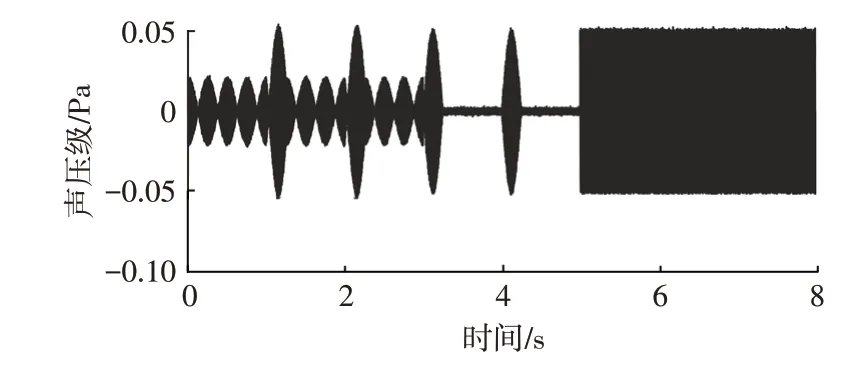
图7 高噪声预警信号时域图

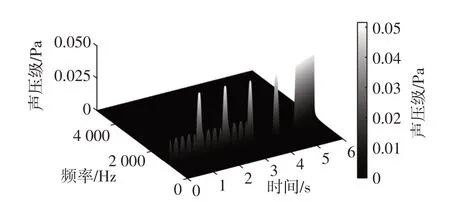
图8 高噪声预警信号时频图

3.2.2 准确提取高噪声信号预警时间

由图7 可知，当声音信号含有噪声时，无法直接从信号的时域图中判断信号的预警时刻。可从频域进行分析，利用短时傅里叶变换结合时、频域时间误差校正预警时刻，校正后预警时刻如图9所示。由图9可知，预警起始点都可准确计算获得，与仿真数值中给定的时间进行比较，几乎无误差，表明该方法计算预警时间准确率高。

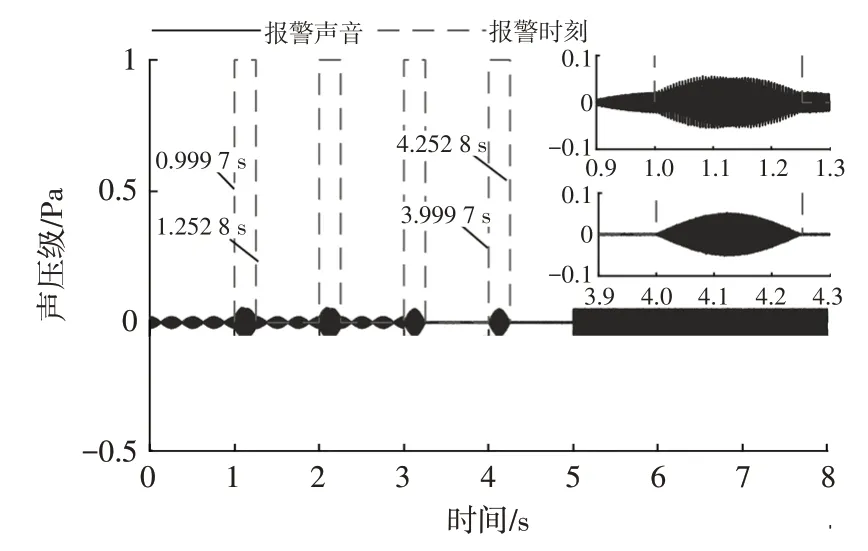
图9 高噪声预警时刻校正

此外，前3 s 的信号频率满足在[950,1 050]Hz 的范围内，但幅值不满足在[0.03,0.07]Pa 的范围内，信号后3 s幅值满足在[0.03,0.07]Pa的范围内，但频率不满足在[950,1 050]Hz 的范围内，均被屏蔽，说明该方法能较好地屏蔽外界的干扰噪声。将最大幅值的识别范围设置为[0.01,0.09]Pa，得到的信号预警时刻如图10 所示，因幅值识别范围的扩大，计算的结果会把外界干扰信号识别进来，造成误判断，进一步体现出本文方法的优势。

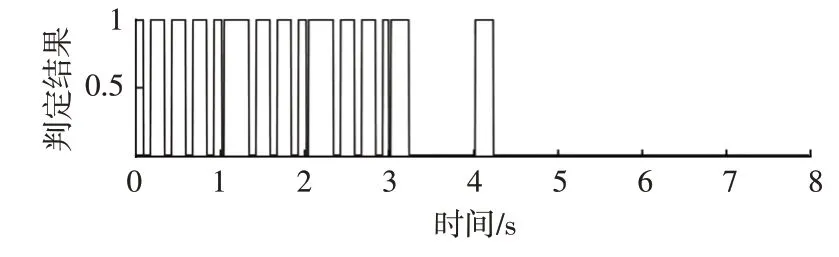
图10 高噪声预警声音预警时刻误判

4 试验测试及算法验证

4.1 试验测试

按照标准JT/T 1242—2019 进行AEB 系统试验，利用国内某款客车作为测试车辆，该车辆具备AEB功能，装配有毫米波雷达和摄像头。本次试验采用的设备包括RT 3002 机械陀螺仪、双车通信模块RT ranger、GPS差分基站、IMC 通用数据采集器、采集预警声音的PCB麦克风以及工程验证测试（Engineering Validation Test，EVT）假车，如图11所示。

图11 试验设备及车辆测试工况

为了验证方法的准确性，进行目标车辆静止工况的自动紧急制动测试，自车速度40 km/h，距离目标车辆150 m 时，测试开始，测试过程中驾驶员保持油门踏板位置维持车速恒定。

4.2 试验结果计算与分析

4.2.1 低噪声信号滤波及频域分析

AEB 系统试验中，系统会发出两级预警的声音，为了后期进行分析，正式测试前在较安静环境下分别采集预警声音并进行无相位滤波，再进行时域和频域分析。采样频率为20 kHz，因本试验不需计算声音的大小，所以测试过程中未对麦克风灵敏度进行校正。将预警信号先进行无相位带通滤波，通带范围为[500,5 000]Hz，阶数为200 阶。再进行短时傅里叶变换，窗长选用1 000 个数据点，重叠率为99%，选取汉宁窗，频率分辨率为20 Hz。一、二级预警时频域分别如图12、图13 所示，从图12、图13 中可知，一、二级预警的最大幅值对应的频率分别为1 560 Hz和2 000 Hz，一、二级预警的最大幅值分别为0.050 2 Pa和0.089 1 Pa。设置一级预警的频率识别范围为[1 520,1 600]Hz，幅值识别范围为[0.03,0.07]Pa；设置二级预警的频率识别范围为[1 960,2 040]Hz，幅值识别范围为[0.03,0.15]Pa。

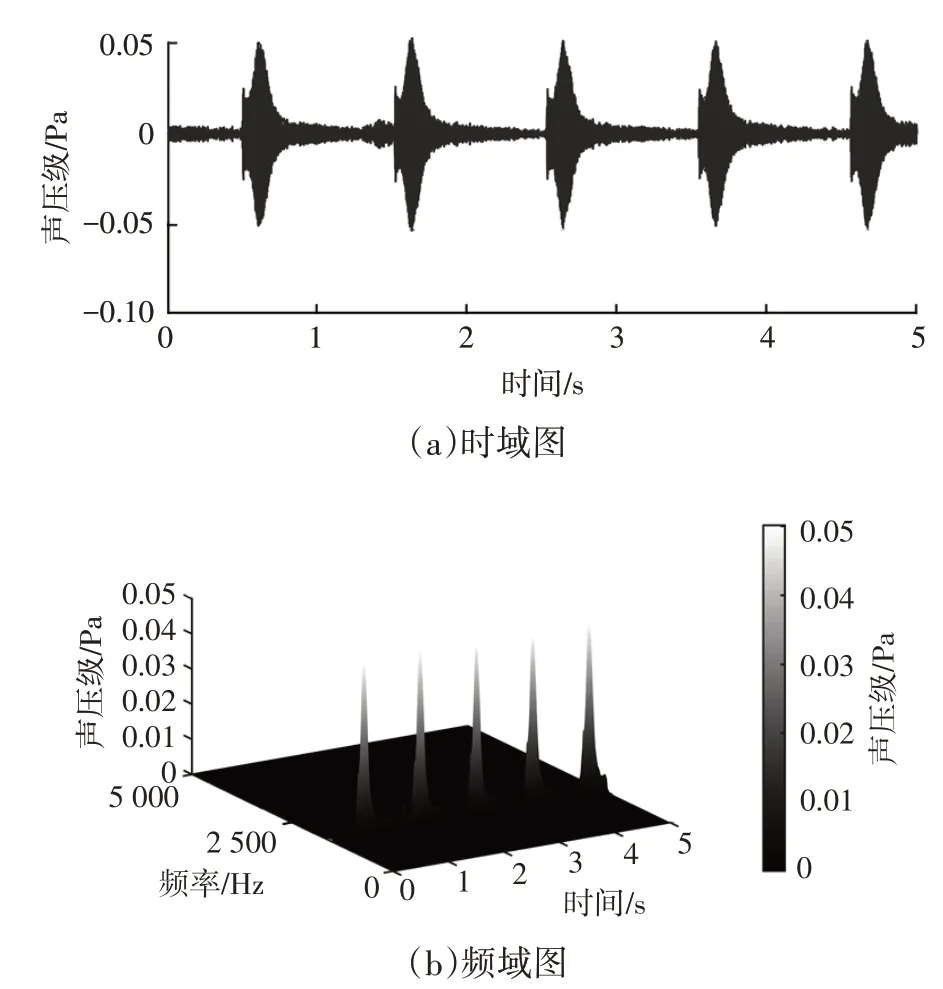
图12 低噪声一级预警时频域图

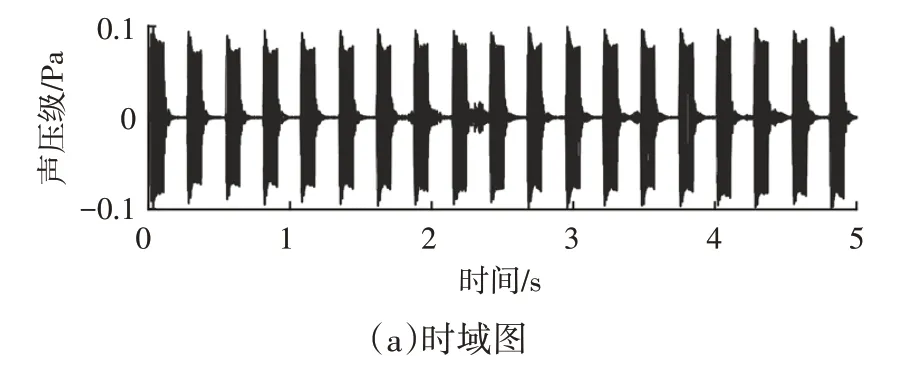
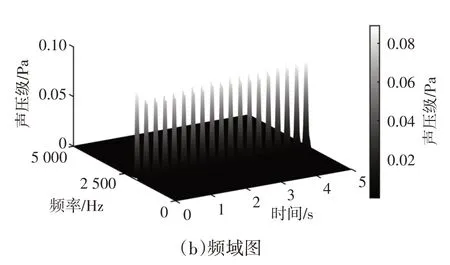
图13 低噪声二级预警时频域图

4.2.2 低噪声信号时域法获取预警时间

将低噪声预警信号先进行无相位带通滤波，再进行Hilbert 变换求得包络来识别预警时间，一、二级预警信号包络如图14所示。

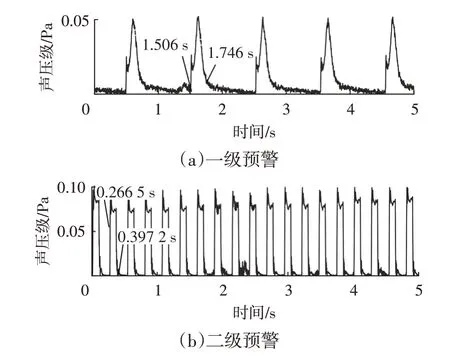
图14 低噪声一、二级预警信号包络

4.2.3 低噪声信号频域法获取预警时间

将无相位带通滤波后的低噪声预警信号进行短时傅里叶变换，每个窗长的最大幅值及其频率满足设定的频率和幅值范围时，将该时刻的结果设定为1，反之，该时刻的结果设定为0。计算得到的一、二级信号预警时刻如图15所示。

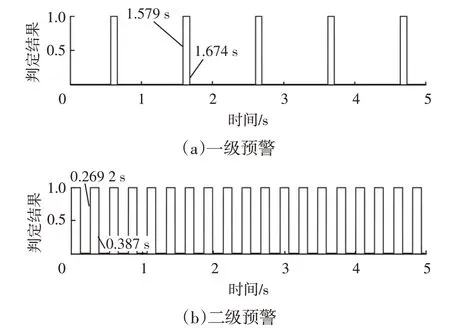
图15 低噪声一、二级预警时刻

4.2.4 低噪声信号时域和频域法时间差校正

JT/T 1242—2019 要求一级预警到紧急制动的时间大于1.4 s，二级预警到紧急制动的时间大于0.8 s。结合图14和图15，两者的预警时刻误差较大，其中一级预警的误差达到0.073 s，会极大地影响测试结果，造成测试结果误判。将预警时刻按照包络提取和短时傅里叶变换进行校正，校正后预警时刻如图16所示，预警时刻与预警声音相符。

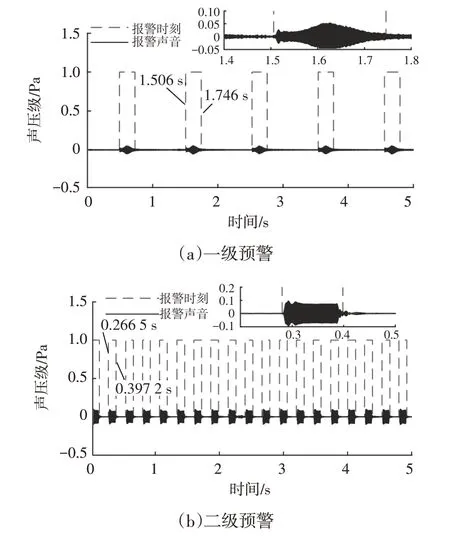
图16 低噪声一、二级预警时刻校正

4.2.5 试验结果

目标车辆静止进行测试，自车速度40 km/h，采集试验过程的预警声信号如图17所示。由于采用1个麦克风采集整个试验过程中的报警声音信号，为了进行声音报警时间识别，需要将信号进行分离。先将预警信号进行无相位带通滤波，范围分别为[1 300,1 800] Hz 和[1 800,2 200]Hz，得到高噪声的一、二级预警信号。再将预警声音按照包络提取和短时傅里叶变换校正法得到的预警时刻如图18所示。从图18中可知，预警时刻与预警声音吻合，验证了方法的准确性。

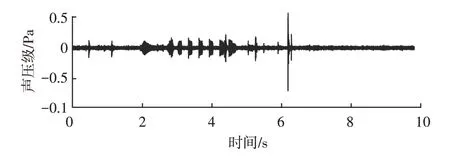
图17 高噪声预警信号时域图

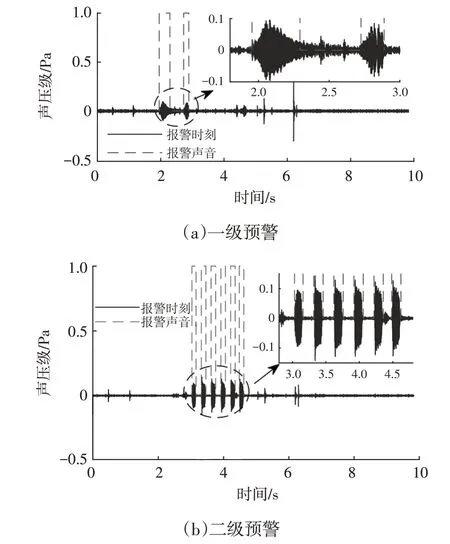
图18 测试信号一、二级预警时刻校正

AEB 系统试验与预警时间有关的参数是距离碰撞时间（Time To Collision，TTC）和制动加速度，所以此处仅分析这2 个量，测试中加速度和TTC 信号如图19 所示。测试结果如表1 所示，t1和t2分别为一级和二级预警时刻相对于紧急制动时刻的时差，tc1、tc2和tc3分别为一级预警时刻、二级预警时刻和紧急制动阶段（以至少4 m/s2的减速度开始减速的阶段）的TTC，由测试数据可知，测试结果满足标准要求，但本试验报警时刻误差较大时将会直接导致结果的误判。

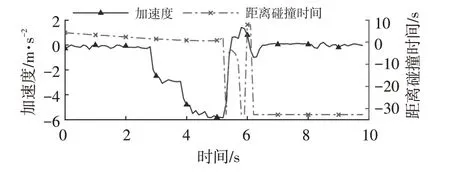
图19 测试信号加速度和距离碰撞时间

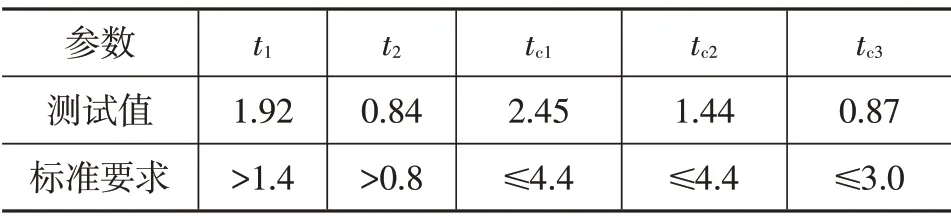
表1 试验结果 s

5 结束语

本文提出一种结合短时傅里叶变换和信号包络的AEB系统测试预警时间准确提取方法，先分别利用短时傅里叶变换和Hilbert 包络从频域和时域计算低噪声预警信号的时间，并进行短时傅里叶变换得到预警时间的误差时间，再利用短时傅里叶变换和误差时间准确提取高噪声信号预警时刻。建立了试验车辆预警声音的仿真信号，仿真结果表明，频域法提取预警时刻有较大误差，由时域法提取预警时刻易造成误判，通过本文所提出方法计算的预警时刻与仿真中真实时刻相比误差很小，并能够屏蔽外界干扰噪声。

在某客车上进行的目标车辆静止工况的自动紧急制动测试结果表明，未校正的一级预警到紧急制动的时间的误差达到0.073 s，会造成测试结果误判，而校正方法计算的预警时刻与实际的预警声音吻合，验证了方法的准确性。

本文所提出的方法还可直接应用在车道偏离预警、前撞预警、车道保持系统等主动安全测试中，在测试噪声较大时得到准确的预警时刻。