基于EMB的纯电动汽车制动稳定性与制动能量回收多目标优化

彭伟 李志华 陈启鹏

（杭州电子科技大学，杭州 310018）

主题词：纯电动汽车 制动稳定性 制动能量回收

1 前言

相比于传统的液压制动系统，电子机械制动（Electro-Mechanical Braking，EMB）系统结构简单、制动响应迅速、制动能效高、灵敏度高，且易于和其他系统进行综合控制，将其与轮毂电机、蓄电池/超级电容相结合将大幅提高整车的能源利用率和动力性能，同时也是目前新能源汽车研究的新方向。

目前的研究中对EMB系统的再生制动能量回收系统[1]研究甚少。为此，本文采用粒子群优化算法对再生制动回收目标函数和稳定性目标函数进行最优求解，以提高纯电动汽车的再生制动能量回收率与制动稳定性，并利用ADVISOR软件建模对最优解集进行仿真验证。

2 整车动力学模型

2.1 电子机械制动系统

2.1.1 EMB系统执行机构工作原理

本文的研究对象为某型纯电动汽车，前轮、后轮共配有4个电子机械制动器，后轮配备2个轮毂电机，车辆转弯时会节省更多能量，且加速、爬坡能力强，驱动性能更好。将蓄电池/超级电容混合使用，能充分发挥超级电容比功率大、蓄电池比能量大的优势，同时也满足了电动汽车对比能量大、比功率大的双重要求，大幅延长了电动汽车续驶里程。

本文研究的EMB 系统主要由电动机、减速增力机构、运动转换机构3个部分组成，如图1所示。选择无刷直流电动机，减速增力机构选择行星齿轮，运动转换机构选择滚珠丝杆，该滚珠丝杆为螺旋机构，可将旋转运动转换为直线运动并产生压紧力，从而使摩擦片压紧制动盘。

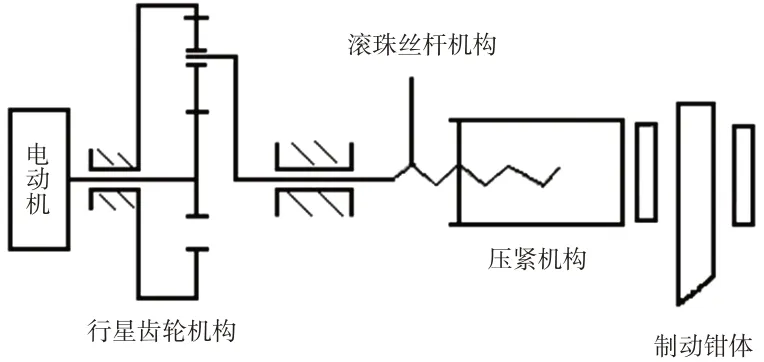
图1 EMB系统执行机构原理示意

2.1.2 EMB系统模型

电子机械制动器模型是一个涉及结构参数、电机参数、控制参数等耦合的模型，其数学模型为[2-3]：

a.无刷直流电动机的数学模型为：

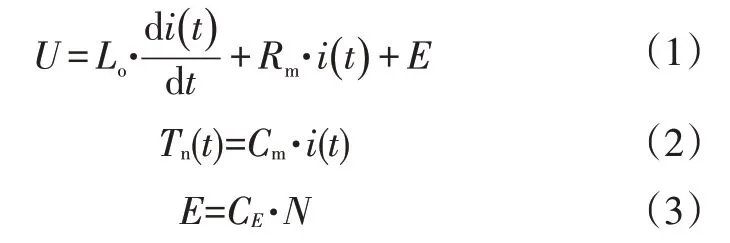
式中，Lo为电枢电感；Rm为回路电阻；U为电枢电压；i(t)为电枢电流；Tn(t)为电动机产生的转矩；Cm为转矩系数；E为电枢反电势；CE为电机感应电势系数；N为转子的转速。

b.行星齿轮减速机构数学模型为：式中，Tx为行星架输出扭矩；Ta=Tn为太阳轮输入扭矩；ix为传动比；ηx为行星齿轮的传动效率。

c.滚珠丝杆副数学模型为：

式中，To为滚珠丝杆的驱动转矩；F为丝杆的推力；Ph为丝杆的导程；ηs为滚珠丝杆的传动效率。

由式（1）～式（6）可得EMB 系统制动力的数学模型为：

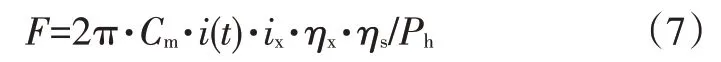
2.1.3 再生制动控制与原理分析

EMB系统根据驾驶员的制动强度和路况由制动控制单元来分配前、后轴的制动力，然后将制动信号发送给执行机构，执行机构通过对制动盘施加合适的制动力实时控制制动钳夹紧力，最终实现车辆制动。纯电动汽车再生制动系统工作原理如图2所示。

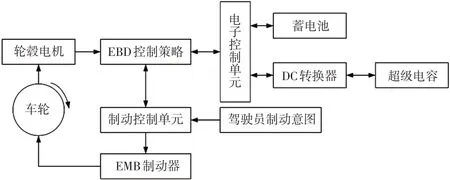
图2 纯电动汽车再生制动系统工作原理

2.1.4 电子制动力分配制动控制策略

由于在进行前、后制动力分配时应使前轮先于后轮抱死且避免后轮抱死，故前、后轮制动力按电子制动力分配（Electronic Brake force Distribution，EBD）控制策略进行分配[4-5]能有效提高车辆稳定性，具体流程如图3所示，其中Fn为需求的总制动力，Freg为再生制动力，Ff为前轴制动力，Fregmax为最大再生制动力。

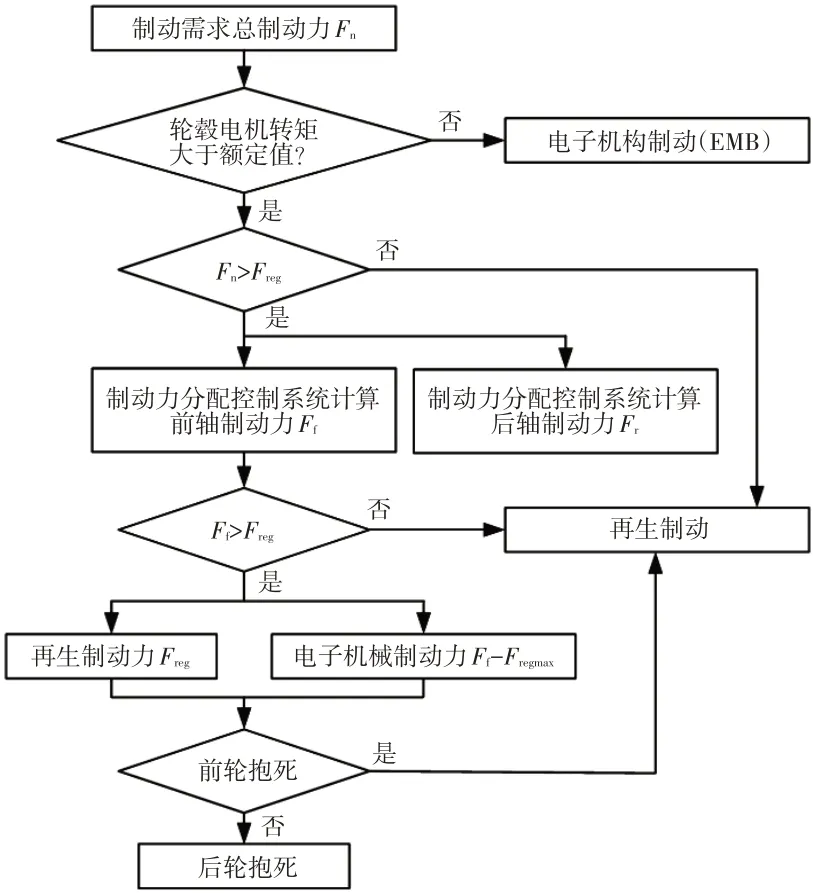
图3 制动能量回收控制策略流程

2.2 轮毂电机模型

纯电动汽车在行驶过程中，轮毂电机转速与车速的关系为：

式中，w为轮毂电机转速；vα为行驶瞬时速度；rw为车轮滚动半径。

轮毂电机的制动转矩与制动力的关系为：

式中，Tm为轮毂电机制动转矩；Fm为轮毂电机再生制动力。

当轮毂电机再生制动反转时，转矩与转速的关系为：

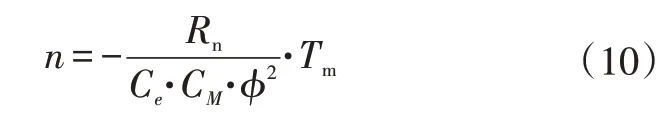
式中，n为电机转速；Rn为电机内阻；φ为磁通量；Ce为电机电势常数；CM为转矩常数。

2.3 双能源系统分析

2.3.1 双能源系统工作原理

超级电容工作电压相对低，蓄电池和超级电容的功率分配采用DC/DC 变换器控制。在超级电容/蓄电池配合的双能源系统纯电动汽车上，蓄电池输出功率应与电动汽车的平均行驶功率相近，当电动汽车的实际行驶功率高于超级电容的最大输出功率时，剩余部分功率优先由蓄电池提供。蓄电池/超级电容的工作原理如图4所示。

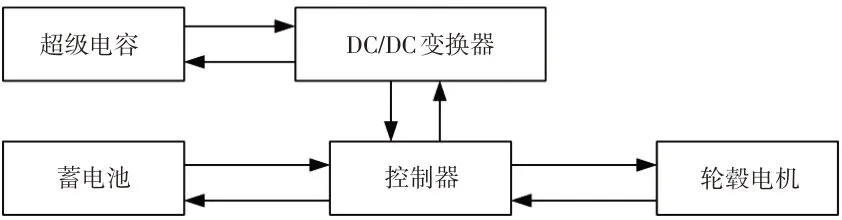
图4 双能源工作原理

2.3.2 超级电容模型

轮毂电机的电流平衡方程为：

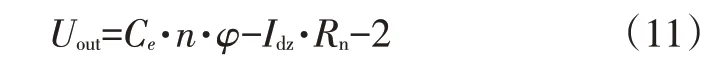
式中，Uout、Idz分别为电枢电压和电流。

根据降压变换器的变换规律，超级电容两端电压Uo应满足：

式中，Umax为充电电压；D为DC/DC 变换器的占空比，本文取D=0.085。

超级电容的充电方程为：

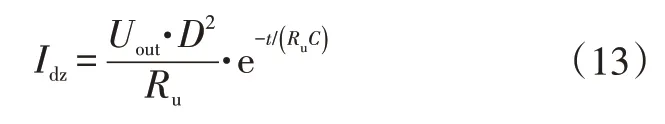
式中，Ru为充电电阻；C为超级电容容量。

超级电容在充电时端电压U(t)为时间t的函数：

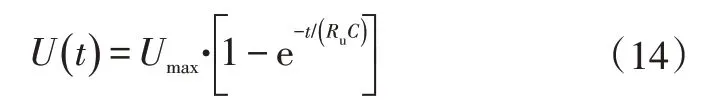
考虑到工作寿命，超级电容应工作在合理的电压范围[Umin,Umax]内，超级电容储存的电量USOC为：

2.3.3 蓄电池模型

蓄电池充电的输入功率Pa为：

式中，Ua为蓄电池的端电压；Ia为蓄电池回路电流。

蓄电池充电端电压方程为：

式中，Ea、Ra分别为跟随荷电状态变化的蓄电池电动势和等效内阻。

故由式（16）、式（17）可得蓄电池充电回路电流方程为：

蓄电池的荷电状态的计算公式为：

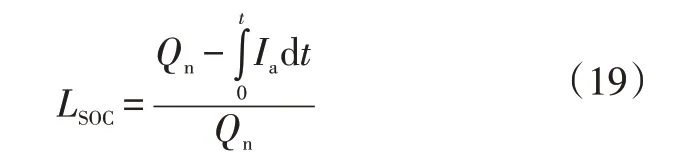
式中，Qn为蓄电池电荷量。

3 再生制动过程分析

电动汽车在制动过程中，制动力同时由电子机械制动系统与轮毂电机再生制动系统提供，则电动汽车提供的总制动力FN为：

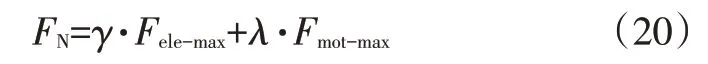
式中，Fele-max为电子机械制动系统提供的最大制动力；γ∈[0,1]为电子机械制动系数；Fmot-max为轮毂电机在当前速度下可提供的最大制动力；λ∈[0,1]为轮毂电机制动力系数。

当需求制动力矩小于轮毂电机所能提供的最大制动力矩时，电子机械制动系统不起作用，γ=0，此时制动力全部由轮毂电机再生制动提供；当需求制动力矩大于轮毂电机再生制动所能提供的制动力矩时，电子机械制动系统工作在最大制动力状态下，λ=1，γ的取值根据工况和需求制动力确定。

4 基于EMB控制的再生制动回收多目标优化

4.1 设计变量

为保证纯电动汽车制动能效和制动稳定性，在满足欧洲经济委员会（ECE）制动法规的前提下，为保证纯电动汽车制动能效和制动稳定性，须将制动力分配系数、蓄电池/超级电容荷电状态和温度控制在合理的范围内，否则会影响再生制动能量的回收率。另外，轮毂电机产生的制动转矩是再生制动能量回收的重要指标，合理的制动转矩能提高制动回收率，故优化设计变量X为[6]：

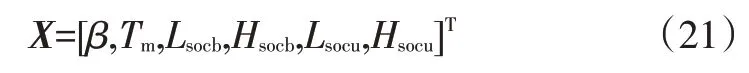
式中，β为电动汽车制动力的分配系数；Lsocb、Lsocu分别为蓄电池电荷量的最小值、最大值；Hsocb、Hsocu分别为超级电容的电荷量最小值、最大值。

4.2 优化的目标函数

4.2.1 制动稳定性目标函数

对汽车进行受力分析，得到纯电动汽车在制动工况下前、后轴利用附着系数δ1、δ2分别为：

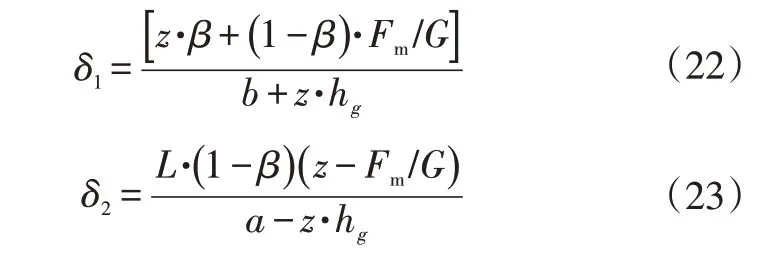
式中，G为整车所受重力；L为轴距；a、b分别为整车质心到前、后轴的距离；hg为整车质心高度；z为制动强度。

汽车越稳定，附着系数越接近制动强度。因此，制动稳定性的目标函数Y1可表示为：

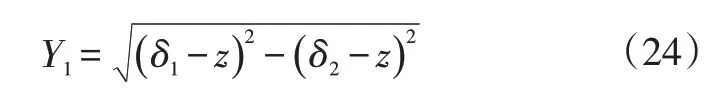
4.2.2 制动回收能量目标函数

纯电动汽车在再生制动过程中，轮毂电机的惯性转动产生的动能转化为电能，最终存储到蓄电池/超级电容中，才能实现制动能量的回收。故轮毂电机的发电效率、蓄电池/超级电容的充电效率直接影响制动能量的回收效率。

轮毂电机的发电效率与电机转速有关，蓄电池/超级电容的充电效率与蓄电池/超级电容的荷电状态、温度有关，故两者的联合效率可表示为：

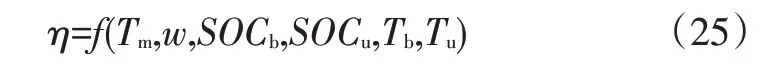
式中，SOCb、SOCu分别为蓄电池、超级电容的荷电状态；Tb、Tu分别为蓄电池和超级电容的工作温度；f为函数关系。

则最大再生制动回收能量的目标函数Y2可表示为：

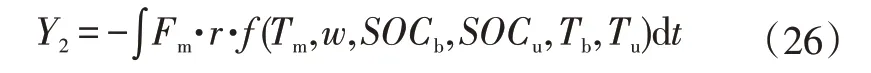
式中，r为车轮半径。

4.3 约束条件

4.3.1 ECE制动法规限制

轮毂电机产生的再生制动力参与制动时，制动力分配系数将在一定范围内变化，故整车制动力分配系数应有合理的上限值。

4.3.2 轮毂电机峰值转矩限制

当制动强度较大时，所需的制动力也很大，此时再生制动力不能单独提供整车所需的制动力，不能满足制动要求的部分由电子机械制动系统配合提供，故轮毂电机的再生制动效果将受最大制动转矩的限制。

4.3.3 蓄电池/超级电容的充电功率限制

蓄电池/超级电容的荷电状态是影响再生制动能量回收的主要因素之一。当其荷电状态较低时，再生制动能量回收能力变强，而荷电状态较高时，不宜对蓄电池/超级电容充电，过度充电会损害蓄电池/超级电容，故再生制动能量回收系统将停止工作。因此，选取合适的蓄电池/超级电容的荷电状态对再生制动能量回收很关键。

综上所述，本文所确定的目标函数需满足如下约束条件：

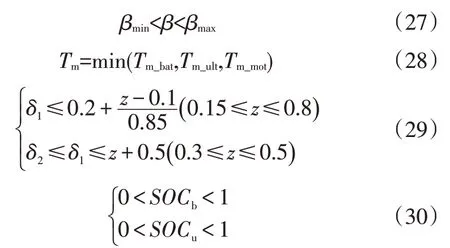
式中，βmin=0.5、βmax=0.8分别为再生制动分配系数的下限值和上限值；Tm_bat、Tm_ult分别为满足蓄电池/超级电容最大充电功率的轮毂电机再生转矩上限；Tm_mot为满足轮毂电机峰值转矩的再生转矩上限。

4.4 多目标粒子群优化算法

多目标优化问题需要同时优化多个目标函数，可以表述为[7-8]：

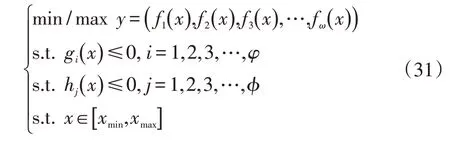
式中，fω(x)为目标函数；gi(x)、hj(x)为约束条件。

在多目标学科设计优化软件Isight 中，利用多目标粒子群优化（Multi-Objective Particle Swarm Optimization，MOPSO）算法进行自动搜索及迭代运算，实现对纯电动汽车电子机械制动系统关键参数的优化，如图5 所示[9-10]。其中，设置最大迭代次数为50 次，粒子数量为20 个，粒子最大速度为0.1 m/s。在优化过程中，EMB制动器中的行星齿轮主要参数为：太阳轮齿数z1=25、行星轮齿数z2=35、内齿轮齿数z3=88、传动比ia=6.073、模数m=1.25，滚珠丝杆导程为0.008 m。轮毂电机额定功率、峰值功率分别为5 kW、15 kW，额定扭矩、峰值扭矩分别为20 N·m、70 N·m。

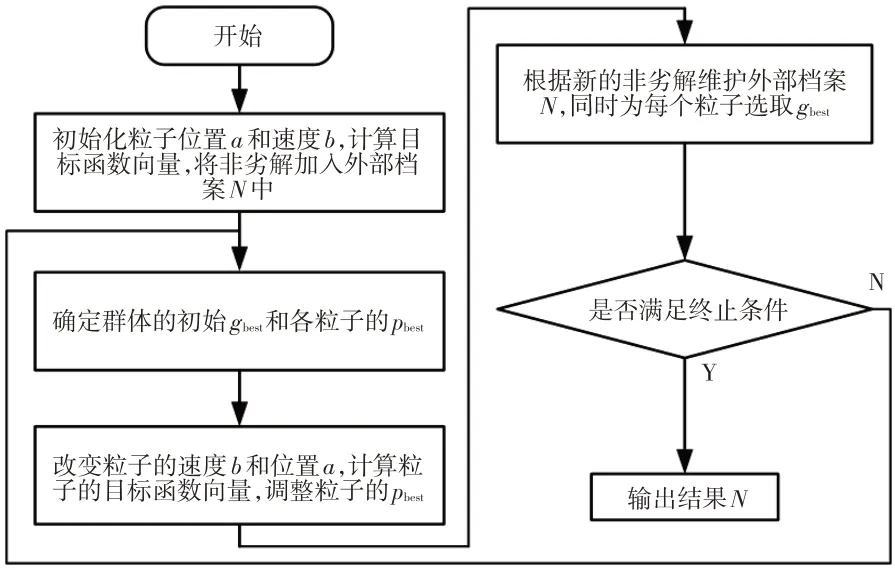
图5 MOPSO算法计算流程

将模型参数在Isight 软件中设置好后，得到优化目标从开始迭代到最终结束时群粒子在空间寻优的过程，如图6、图7 所示。图8、图9 分别反映了制动稳定性Y1和制动能量回收Y2的寻优解集。优化过程中选取制动强度z为0.10、0.20、0.25、0.30、0.40、0.50、0.55、0.60、0.70。经过选择，选取其中一组优化结果作为优化后的仿真模型参数，如表1所示，其中，Fr为后轮制动力。

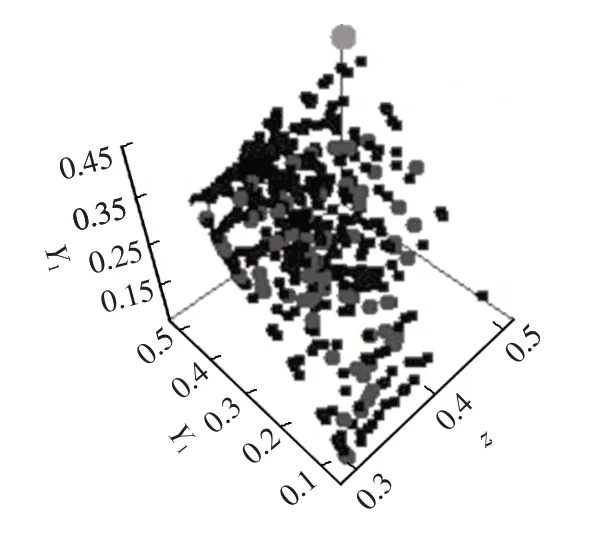
图6 制动稳定性群粒子分布

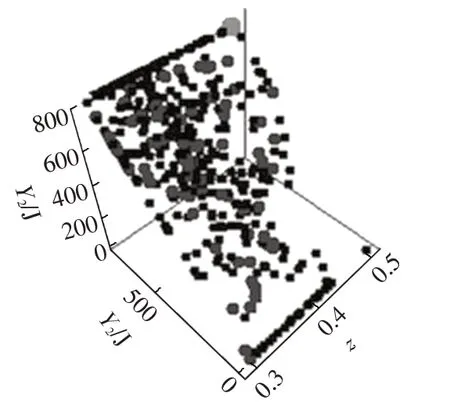
图7 制动能量回收群粒子分布

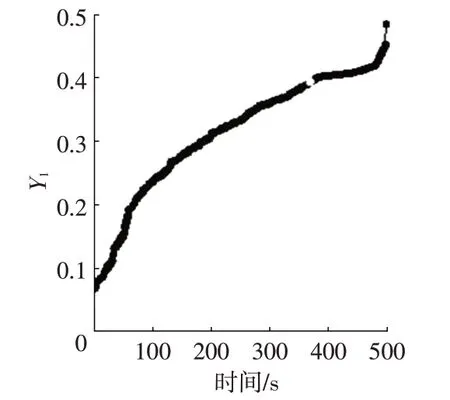
图8 制动稳定性

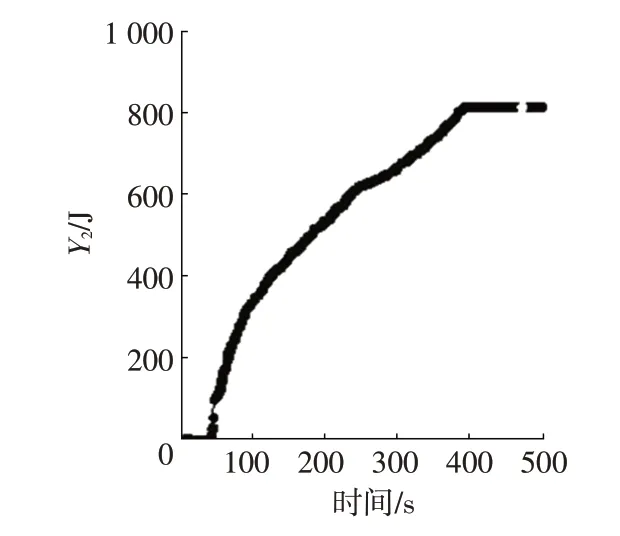
图9 制动能量回收

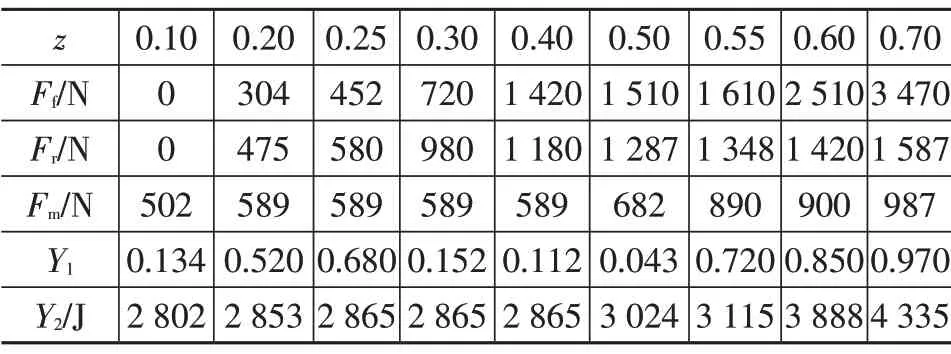
表1 选取参数数据

最优参数结果为：制动力分配系数的下限为0.580、上限为0.754，最优制动力分配系数为β=0.68，再生制动力矩Tm=145.36 N·m，蓄电池荷电状态的上限为0.90、下限为0.40，超级电容荷电状态的上限为0.95、下限为0.30。根据优化结果选择的永磁直流力矩电机、行星齿轮主要参数为：太阳轮齿数zy=19、行星轮齿数zx=29、内齿轮齿数zn=77、传动比i=5.053、模数m=1.25，滚珠丝杆导程为0.002 m。

4.5 建模仿真分析

通过Simulink 建立双能源模型，在ADVSIOR 软件平台上进行验证，控制策略是基于电子机械制动系统的EBD 控制策略，在进行整车仿真时，忽略制动器传递损失效率、制动滞后等因素。

在Simulink 中建立EMB 制动器、轮毂电机、双能源系统仿真模型如图10所示。

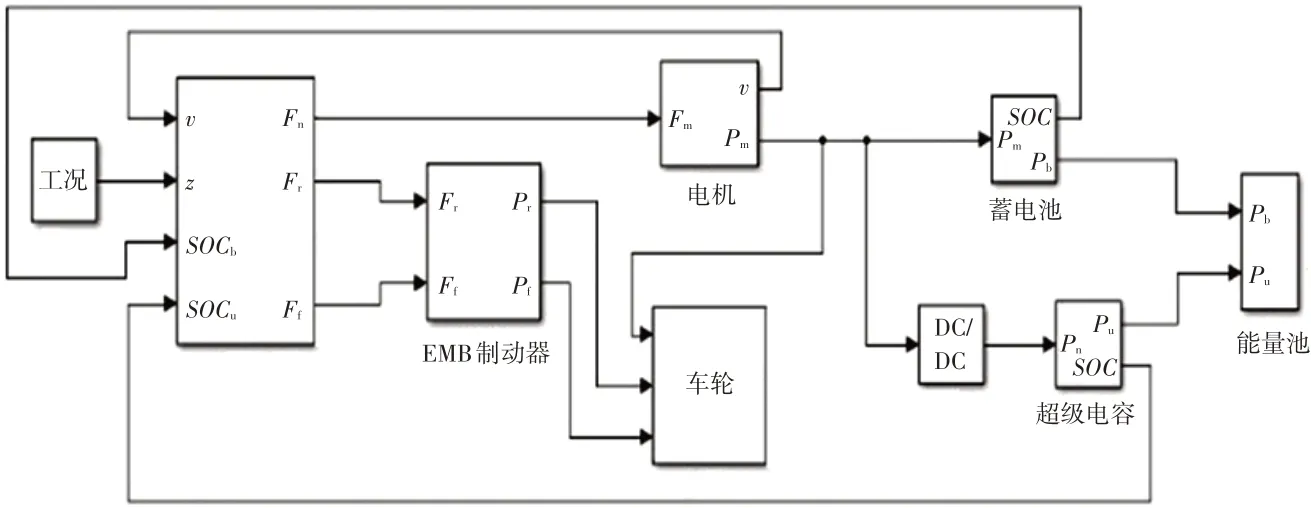
图10 Simulink仿真框图

为了验证优化结果对双能源电动汽车的制动性能的影响，在典型ECE 工况、NYCC 工况、UDDS 工况下进行对比仿真分析，模型如图11 所示，整车模型参数如表2所示。

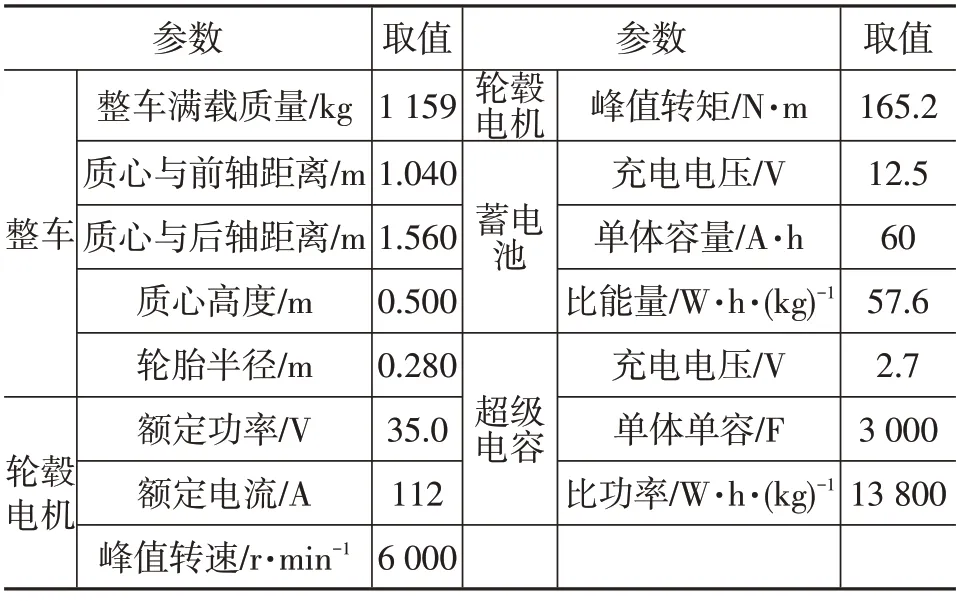
表2 整车模型参数

图11 纯电动汽车ADVISOR仿真模型

通过ADVSIOR软件的仿真验证，使用优化前、后的参数在ECE、NYCC、UDDS 工况下进行验证，得到蓄电池/超级电容荷电状态、再生制动能量回收曲线如图12～图14所示。

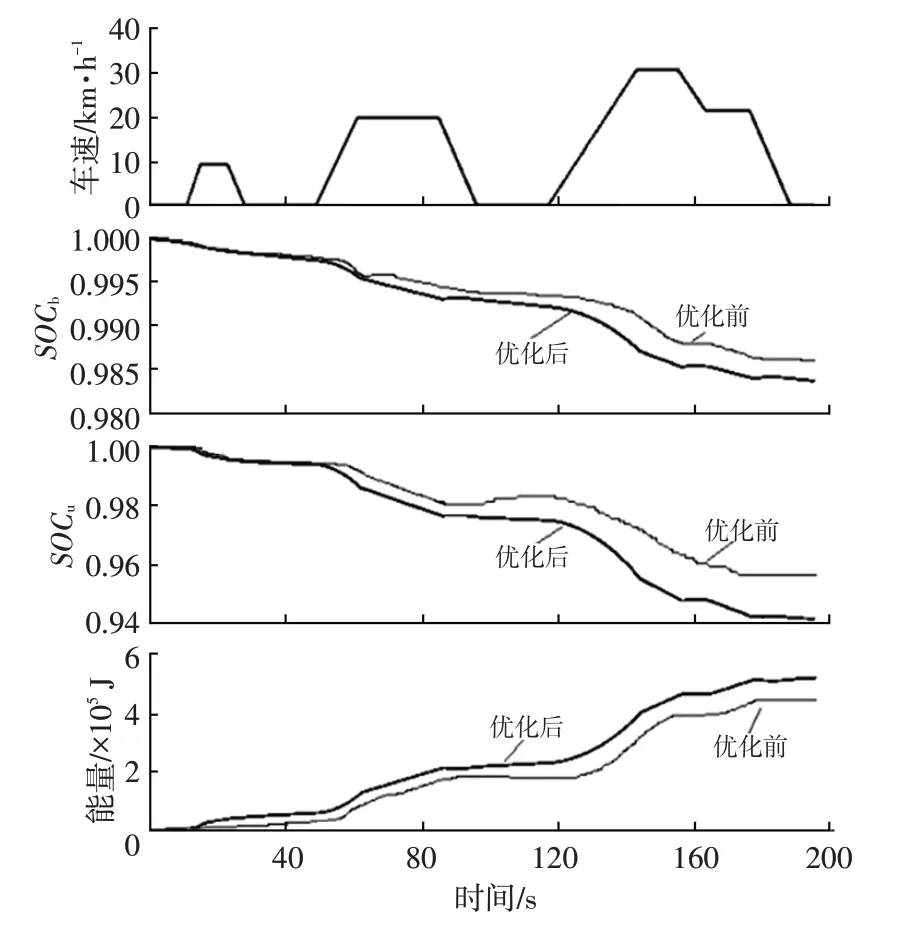
图12 ECE工况优化结果

本文优化算法与其他再生制动优化策略在ECE、NYCC、UDSS 制动工况下，制动过程中总的制动能量回收效率对比如表3所示。

由图12～图14可以看出：该纯电动汽车在3个典型工况下，优化后的再生制动能量回收率都得到有效提高且续里航程增加；在相同速度、不同工况下，制动回收的能量不同，且在NYCC工况下行驶时制动能量回收率最大，UDDS 工况制动能量回收率次之；电动汽车在ECE工况与UDDS工况下行驶得到的制动回收能量相比，其优化后的制动能量回收率相近，但蓄电池/超级电容的荷电状态变化相差较大。

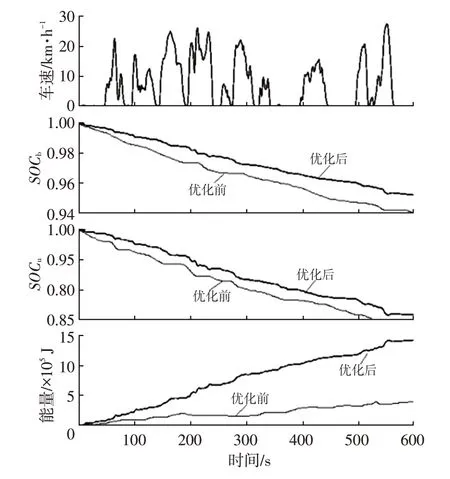
图13 NYCC工况优化结果

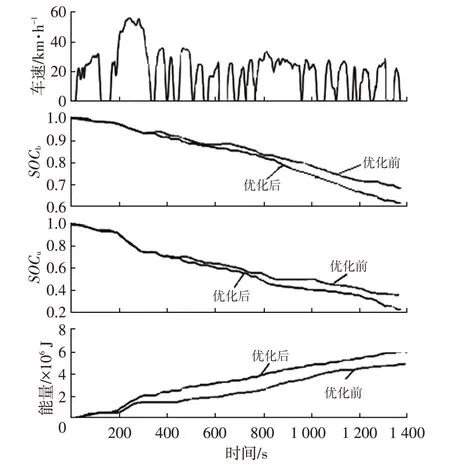
图14 UDDS工况优化结果

由表3可知：本文优化方法相比传统汽车的再生制动控制策略，在3种工况下再生制动能量回收率都明显提高；而相比遗传算法的优化控制策略，本文优化方法的再生制动能量回收率在ECE工况、NYCC工况下有提高；相比人工神经网络制动力分配控制策略，本文的再生制动能量回收率在NYCC 工况、UDSS 工况下有所提高；在UDSS 工况下，本文优化方法的再生制动能量回收率相比其他3种控制方法提升幅度最大。

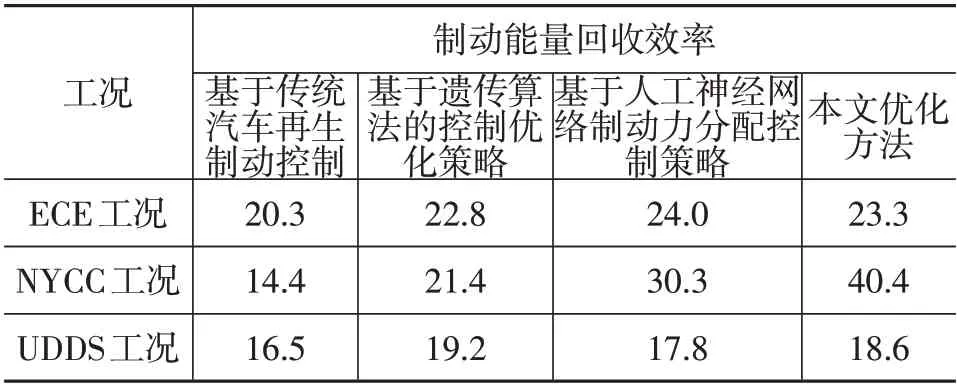
表3 不同工况下制动能量回收效率 %

综上所述，在3种不同工况下，相同的时间内，优化后的制动能量得到提高，利用粒子群优化算法对相关的参数进行Pareto求解最优解集，能够提高以电子机械制动系统为核心的电动汽车的再生制动能量回收率。

附着系数与制动强度的关系反映了汽车制动稳定性，仿真优化后的关系如图15所示。

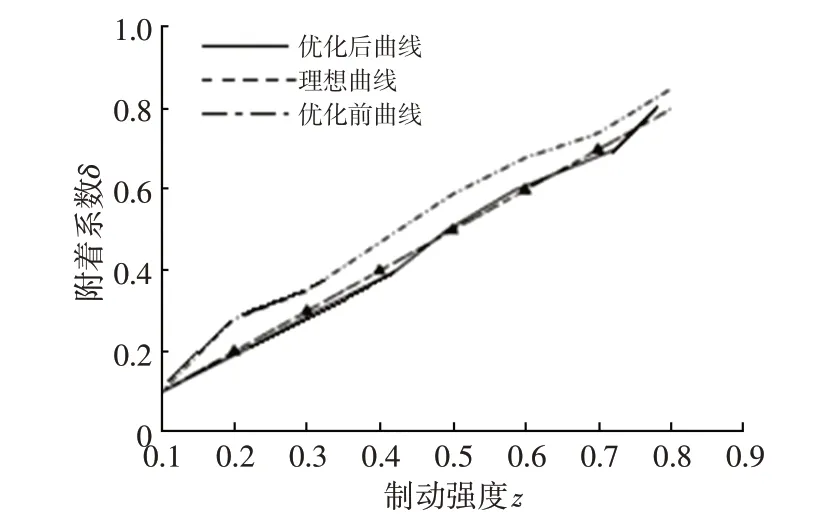
图15 附着系数与制动强度的关系

由图15 可知，当制动强度z=0.5 时，目标函数最接近零，故附着力系数最接近制动强度，汽车稳定性最强。

5 结束语

本文针对电子机械制动系统，先利用Isight 软件进行多目标仿真优化，求得系统参数最优解，再用ADVISOR 汽车仿真软件对其优化结果进行仿真验证，在典型工况ECE、NYCC、UDDS 下进行仿真优化，结果表明，该纯电动汽车能量存储系统参数优化后再生能量回收率得到明显提高，不同工况下得到的再生能量回收幅度不同，仿真结果表明，在NYCC工况下，再生制动回收能量提高幅度最大。