扩大斜切式缓冲结构对时速400 km铁路隧道口微气压波缓解研究
2021-11-13王田天龚彦峰杨明智熊小慧踪敬良陆意斌
王田天,胡 冲,龚彦峰,杨明智,熊小慧,踪敬良,陆意斌,*
(1. 中南大学 交通运输工程学院,轨道交通安全教育部重点实验室,长沙 410075;2. 湖南大学 机械与运载工程学院,长沙 410082;3. 中铁第四勘察设计院集团有限公司,武汉 430063;4. 水下隧道技术国家地方联合工程研究中心,武汉 430063)
0 引言
随着高速铁路的不断发展,中国高铁的最高运营速度已达350 km/h,但由于旅客出行需求和列车运行能力的矛盾依然突出,国家已开始研发设计时速400 km的高速列车。由于我国地形复杂,山地占国土面积的2/3,在高速铁路建设的过程中需修建大量铁路隧道,而车速的提高不可避免地会加剧车-隧耦合气动效应[1-2]。如图1所示,高速列车鼻尖进入隧道的瞬间,会在车前产生初始压缩波,该压缩波以声速沿着隧道长度方向传播并不断激化,到达出口时会以脉冲形式从隧道出口向外辐射,形成脉冲状的压力波,称之为隧道口微气压波或简称为微气压波[3-5]。微气压波幅值随着列车速度的增加而显著增大,当列车以时速小于250 km通过短隧道时,微气压波幅值基本与列车速度的三次方成正比[6];而随着车速和隧道长度的增加,微气压波幅值可与3倍以上的车速成正比[7]。过大的脉冲状压力不仅对隧道口附近的环境产生不利的影响,同时也会严重影响附近居民的正常生活[8-9]。因此,有效缓解时速400 km高速铁路隧道口微气压波对于铁路隧道的建设以及保障隧道口周围环境和居民安全具有重要的意义。
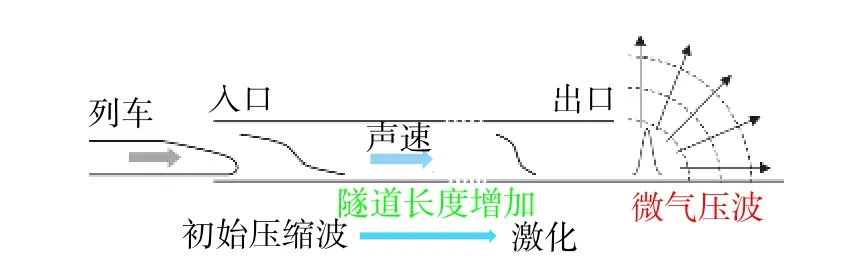
图1 微气压波产生示意图Fig. 1 Schematic diagram of the generation of the micro-pressure wave
在近几十年间,国内外对缓解微气压波的方法进行了大量研究。降低微气压波的基本思路是在压缩波形成和传播阶段减小其压力梯度,现有的缓解方法主要分为两类,一是改变隧道结构(比如在隧道口加设缓冲结构或增大隧道断面面积或修建辅助坑道等)[6];二是改变列车头部形状(增加列车头部流线型长度和改变列车断面面积),从而达到减小初始压缩波最大压力梯度的效果[10]。Yamamoto[11]构建了一个称为“辐射立体角模型”(RSA模型)的预测模型,利用隧道出口周围的立体角来预测地形对微气压波的影响,后来Miyachi[12]扩展了山本的RSA模型,生成了微气压波的声学模型,该模型同时考虑了二阶声源和隧道口周围地形的声学效应。Nagai[13]和Sanetoshi[14]通过数值模拟和动模型试验研究了缓冲结构形式以及优化缓冲结构断面对压力梯度的影响,结果发现优化后能显著降低初始压缩波的压力梯度。贺旭洲等[15]利用数值模拟对斜切式洞门缓冲结构开口率进行了优化分析,并给出了不同车速下的最优开口率。Zhang等[16]使用1/20比例的动模型试验研究了倾斜的隧道口对微气压波的影响。Wang等[17]研究了改变隧道断面参数对压力波动的影响。此外,有学者对缓冲结构缓解微气压波的机理进行研究。周丹[18]认为等截面扩大段缓冲结构使列车前空气在进入隧道前提前被压缩,从而增大了压力上升到最大值的时间;且缓冲结构将压力上升分为了两个或三个阶段,从而压力梯度峰值得到减小。郑长青[19]和牛纪强[20]等认为开口式缓冲结构对初始压缩波幅值基本没有缓解效果,但是可以增加压力上升的时间,从而降低压力梯度达到缓解微气压波的效果。
近几年开始有学者对更高速度下列车隧道空气动力学问题进行研究。吴剑等[21]开展了时速 300 km至350 km高速铁路双线隧道微气压波激化作用及缓解措施研究。范胜利等[22]研究了一种带有排气管的扩大等截面式的新型缓冲结构,且给出了排气管的参数限制,认为排气管的长度应小于压缩波前长度的一半;单个排气管的断面积不宜超过缓冲结构断面面积的20%;并可以针对不同的车速调节排气管的长度或改变排气开孔的位置或数量以达到有效减缓微气压波的目的,但此新型缓冲结构是在车速360 km/h下进行的研究,其对更高车速下微气压波的缓解效果的普适性需进行深入研究,而本研究车速为400 km/h,且缓冲结构带有斜切和开孔,气动效应也更为复杂。魏雨生等[23]对高速列车以时速400 km通过隧道时的列车和隧道压力变化进行了数值模拟,发现车体表面和隧道壁面最大压力变化幅值比300 km时分别提升了90.4%和65.3%,但未对隧道口的微气压波进行研究。
综上,目前国内外针对高速列车以时速400 km通过隧道时的微气压波的缓解方法研究较少,存在较大空缺。故本文以时速400 km高速列车经过隧道引发的微气压波问题为导向,对隧道长度、缓冲结构长度和缓冲结构开孔个数等多个参数展开耦合研究,以期为缓解时速400 km高速铁路隧道口微气压波的缓冲结构设计提供参考。
1 数值计算方法
1.1 数值计算模型
高速列车模型如图2所示,由于微气压波主要与车头的形状相关,故选用2车编组(头车 + 尾车)的复兴号高速列车组(型号:复兴号400-AF)为研究对象,同时对转向架、受电弓、门窗等基本不影响计算准确性的结构进行简化,保留列车的典型气动外形。我国现有运营速度350 km/h的高速列车,主要在京沪、京张等线路上运行,其隧道选用断面积为100 m2的典型高铁双线隧道,两列车的线间距为5 m[24],如图3所示。本文选取此隧道断面进行研究。由于相关研究表明缓冲结构斜切角为30°、扩大段面积与隧道断面积比约为2∶1时,对微气压波有较好的缓解效果[16]。故本文选取了斜切角为30°的等截面扩大段(扩大段面积S扩= 200 m2)的缓冲结构为研究对象,分析其长度和开孔率对时速400 km高速铁路隧道口微气压波的缓解效果。如图4所示,缓冲结构斜切部分的长度为22.56 m,有研究表明列车以一定速度通过隧道,当等截面缓冲结构的长度超过4倍的隧道等效水力直径时,微气压波幅值不再随缓冲结构长度的增加而变化[18]。本文模型隧道的等效水力直径为11.6 m,且缓冲结构带有斜切和开孔,列车速度更高,所以本研究缓冲结构的总长度L在本研究中设置4种,分别为68.56 m、78.56 m、88.56 m和98.56 m;每个开孔的面积为6 m × 4 m,两孔间间隔均为4 m,不同开孔数的工况设置为:1个开孔时为序号①开孔,2个开孔时为①②开孔,3个开孔时为①②③开孔,4个开孔时为①②③④开孔,5开孔时为①②③④⑤开孔。
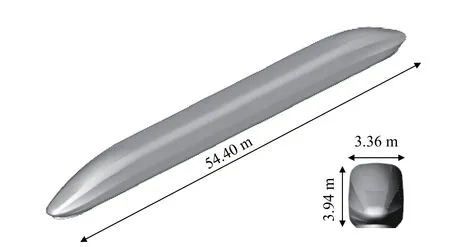
图2 两车编组高速列车模型Fig. 2 High-speed train model of a two-car marshalling
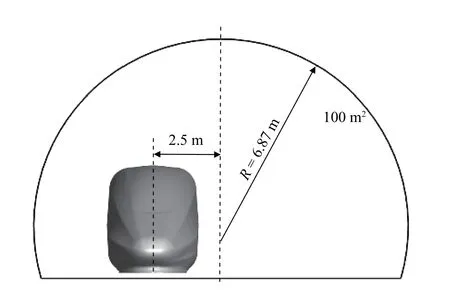
图3 100 m2双线隧道断面Fig. 3 Cross-section of a 100 m2 double-track tunnel
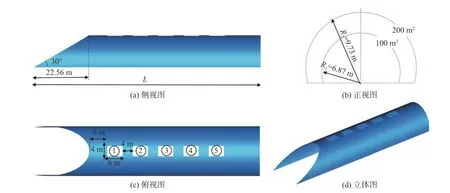
图4 研究缓冲结构长度和开孔个数影响时所采用的几何模型(S隧 = 100 m2,S扩 = 200 m2)Fig. 4 Geometric model used to study the influence of the tunnel-hood length and the number of opening holes (S隧 = 100 m2,S扩 = 200 m2)
1.2 计算区域和边界条件
计算区域如图5所示,分为静止区域和滑移区域2个部分,静止区域又包含列车进口大气区域、隧道(长度L0因工况而定)和列车出口大气区域。考虑到流场和尾流扰动的充分发展,从隧道的两端分别向两侧各延伸450 m。计算域中列车进口大气区域的地面和与隧道接触的面定义为无滑移壁面,其他边界定义为压力出口;在列车出口大气区域中,地面和与隧道接触的面定义为无滑移壁面,其余边界均设置为压力远场边界;隧道和列车均设置为壁面边界条件[25];包含列车的滑移区域的两端分别定义为压力入口和压力出口边界,且在滑移区域和静止区域之间设置交换面以实现数据交换。另外,值得注意的是,由于本文中的流动为三维可压缩气体的不等熵流动,故所有壁面边界条件均为绝热壁面,所有边界初始温度均设置为300 K。
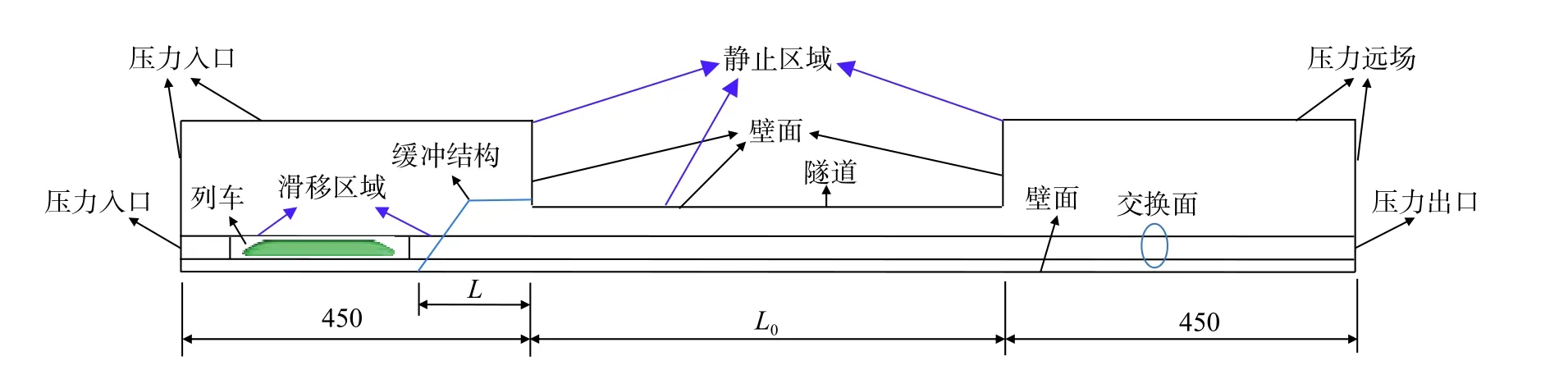
图5 计算区域和边界条件(单位:m)Fig. 5 Computational domain and boundary conditions (unit: m)
1.3 网格划分
如图6所示,本研究采用的高速列车外形复杂,且在隧道口设置了带斜切的缓冲结构,因此选择混合网格对计算域进行离散。列车周围区域及斜切缓冲结构的部分区域离散为非结构化网格,其余部分离散为结构化网格,列车表面上的最小网格尺寸为0.05 m,隧道表面最小网格尺寸为0.15 m。为了对网格的无关性进行检验,按上述的方法调整网格参数,将下文2.1节中的动模型试验的列车和隧道划分为粗、中、细三种网格(其中中网格划分策略与本文选用的网格划分策略一致),网格单元总数分别为4.32×106、9.74×106、1.728×107。选取列车中部测点和隧道中部测点的压力峰-峰值与实验结果进行比较,三种网格的网格密度和压力峰-峰值的偏差结果列于表1。由表1可知,粗网格计算得到的列车表面和隧道壁面的压力峰-峰值较实验的偏差分别为−2.9%和−3.6%,而中等数量网格的列车和隧道的偏差分别为1.2%和−1.6%,细网格的偏差与中等网格基本一致,可以看出粗网格计算的结果与对比实验偏差较大。进一步细分网格,当网格数量超过9.74×106时,计算结果随网格数量增加变化较小,证明网格已经收敛,同时说明9.74×106的中等数量的网格可以同时满足计算精度和计算效率两方面的要求,所以本文选取中等网格划分策略进行研究。
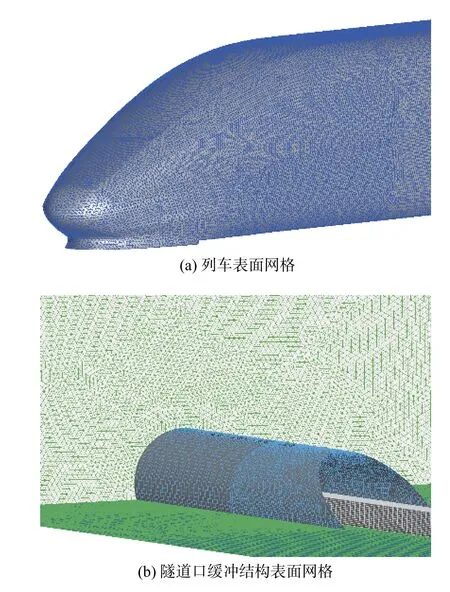
图6 计算网格分布Fig. 6 Computational grid distribution
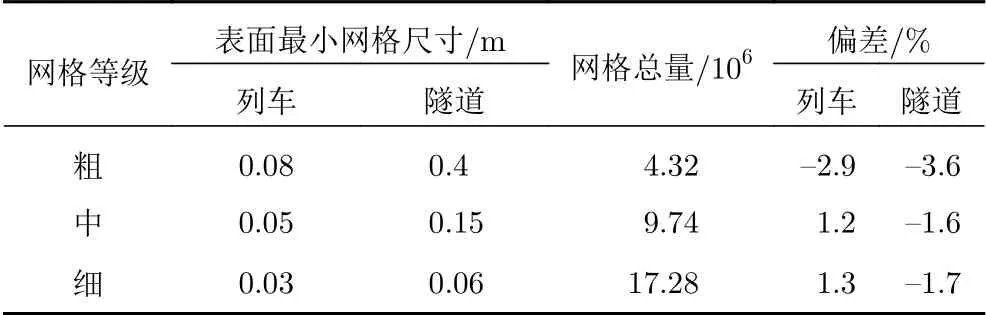
表1 网格密度及峰-峰值的偏差Table 1 Grid density and the peak-to-peak value deviation
1.4 计算方法及求解设置
本研究选用的求解软件为基于有限体积法的ANSYS FLUENT求解器。高速列车通过隧道时,由于空气受到隧道和车体壁面的束缚,需考虑空气的压缩性[26-27]。因此,本文选用基于可压缩 N-S方程的RNGk-ε湍流模型,并采用滑移网格技术,对高速列车通过隧道时的复杂空气流场进行求解[28-29]。速度和压力的耦合方式选用SIMPLE 算法,基于格林高斯的单元法来控制梯度变化,时间离散采用二阶隐式格式,空间离散采用二阶迎风格式[10]。时间步长设置为0.0075 s,并设置50次内部迭代[16]。
1.5 测点布置
因我国对微气压波的评判标准为:距隧道口20 m处的微气压波要小于50 Pa,距隧道口50 m处的微气压波要小于20 Pa[30]。故隧道口微气压波测点分布如图7所示,在距离隧道口20 m、50 m的隧道中线两侧分别对称布置2个测点,靠近列车一侧的测点编号为1和2,远离车一侧的测点编号为3和4,所有测点距离轨面高为1 m。

图7 微气压波测点的布置Fig. 7 Layout of the micro-pressure wave measurement points
2 数值方法验证
2.1 动模型实验
本次动模型试验在中南大学轨道交通安全教育部重点试验室的动模型试验平台进行,该平台可用于单轨试验和双轨试验,主要由三部分组成,分别用于加速、测试和制动[31]。该平台拥有先进的列车穿越隧道和列车交会实验模拟研究系统,并获得CNAS国际认证(注册号CNAS L 10220)和CMA中国国家检测资质认证(证书号170021002479),能够对本文所采用的数值计算方法进行可靠性评价。
如图8,动模型试验采用1∶20缩比模型,列车模型长度为2585 mm,高度为194.5 mm,宽度为163.3 mm;隧道模型对应的实际净空面积为100 m2,长164 m,线间距0.25 m。本次动模型试验的速度为400 km/h,在此平台上一共进行了15次弹射,其中发射速度不在目标速度1%以内的工况不被选用。为记录列车过隧道的产生的压力变化,如图9,在隧道壁面上布置5个测点分别记为S1-S5,其中S3为靠近列车一侧的测点;列车表面布置5个测点,记为T1-T5,如图10。

图8 动模型试验平台Fig. 8 Moving model test platform
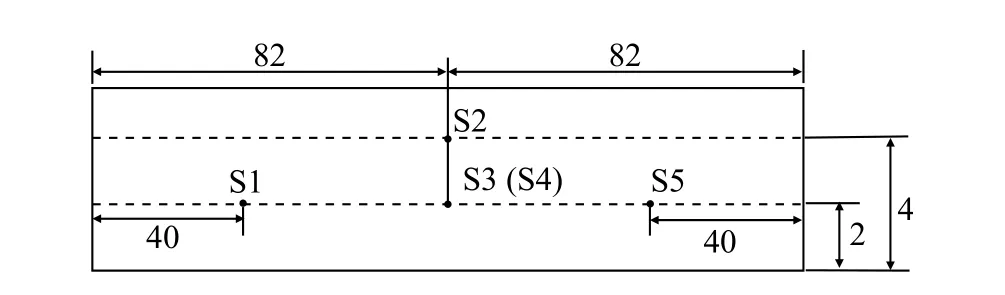
图9 隧道壁面测点(单位:m)Fig. 9 Measurement points on the tunnel surface (unit: m)
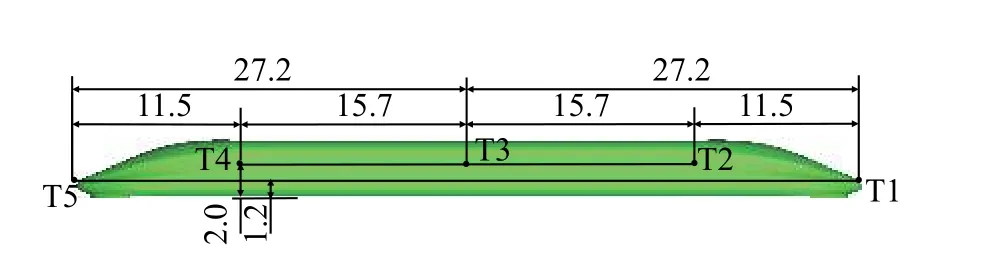
图10 列车表面测点(单位:m)Fig. 10 Measurement points on the train surface (unit: m)
2.2 结果分析对比
按照上文的数值方法对试验模型进行网格划分和模拟计算。由于动模型试验采用的是1∶20的比例,所以试验时间要进行相应转换,同时由于雷诺数大于3.6×105,模型尺寸对列车周围的流场影响很小,因此试验测点的压力值可以代表全尺寸模型的压力值[32]。图11(a)和图11(b)分别为隧道壁面测点S3和列车表面测点T1的压力时程曲线,发现与动模型试验相比,两测点的压力峰-峰值的偏差分别为−1.4% 和1.1%,证明本文的数值方法能够正确反映压力极值的变化规律。图11(c)为图11(a)中隧道壁面测点初始压缩波的压力梯度时程曲线,可以看出数值模拟和动模型试验的初始压缩波梯度曲线吻合较好,且两者压力梯度最大值的偏差仅为1.2%。由式(1)可知微气压波的压力幅值Δpw与初始压缩波的最大压力梯度成正比[1],所以可以得出数值模拟与动模型试验的微气压波幅值的偏差也为1.2%,这证明本文采用的数值方法具有较高的精度。

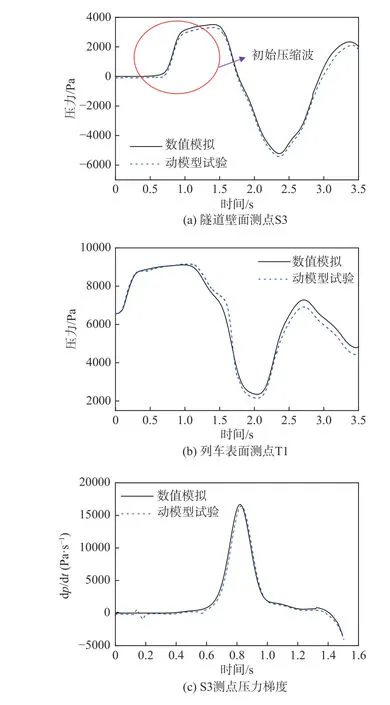
图11 动模型实验和数值模拟所得压力时程曲线对比Fig. 11 Pressure time history comparison between the moving model test and the numerical simulation
3 计算结果和讨论
3.1 无缓冲结构的隧道长度对微气压波的影响
截至2020年底,中国已投入运营的高速铁路隧道共3631座,总长约 6003 km,其中10 km以上的特长隧道只有87座[33],且赵勇等2017的调查结果显示中国高速铁路隧道长度在3 km以下的数量占高速铁路隧道总数的80%以上[34]。可见我国高速铁路隧道绝大多数都在3 km以内,5 km以上的隧道大部分位于群山峻岭,且对应的列车设计时速较小。因此本文选取1 km、2 km和5 km的隧道长度进行研究。
图12为时速400 km高速列车通过长度1 km隧道时,距隧道口20 m处同一截面上对称的两个测点(测点1和测点3)和距隧道口50 m处截面上对称的两个测点(测点2和测点4)的微气压波曲线图,可以发现同一截面上对称的两测点曲线基本吻合,这说明微气压波在同一截面上相同高度的强度相同。所以本文选取靠近列车一侧的测点1(距隧道口20 m)和测点2(距隧道口50 m)进行分析。
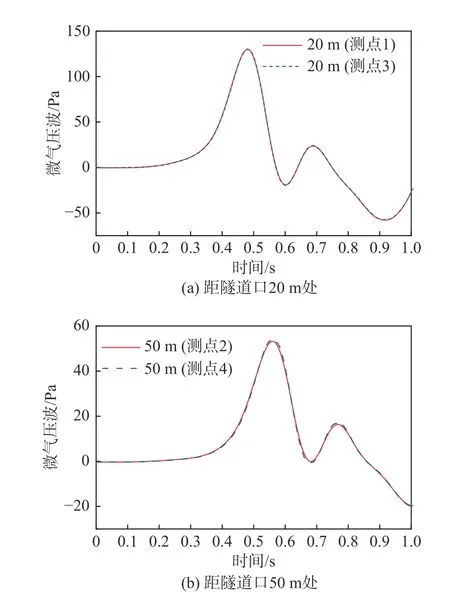
图12 隧道口微气压波曲线图Fig. 12 Micro-pressure wave curves at the tunnel exit
图13(a、b)为高速列车以时速400 km通过长度(L0)为1 km、2 km、5 km的无缓冲结构隧道时,测点1和测点2的微气压波随时间变化的曲线图。可以发现隧道长度在5 km以内时,微气压波幅值随着隧道长度的增加而增大,这是因为初始压缩波在隧道内传播时,由于挤压和摩擦效应,空气密度和温度随之增加,引起声速的提高,使初始压缩波后部比前端传播的更快进而使其激化所导致。
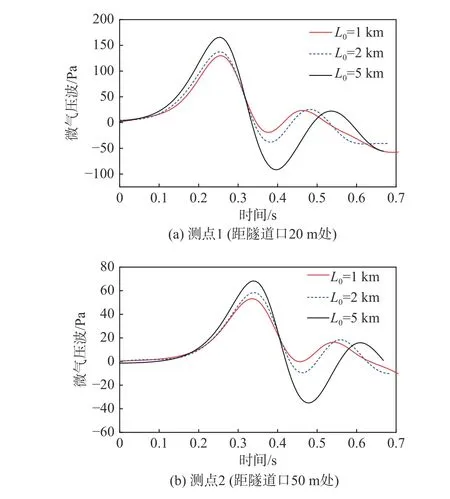
图13 不同隧道长度下微气压波曲线图Fig. 13 Micro-pressure wave curves for different tunnel lengths
表2和表3分别为高速列车通过不同长度隧道时,测点1和测点2的微气压波幅值及相对1 km隧道的增长率。可以发现,在每个测点隧道长5 km的微气压波幅值及相对隧道长1 km的增长率都为最大,测点1和测点2微气压波幅值分别为165.7 Pa和68.3 Pa,微气压波幅值最大增长率分别为27.4%和28.4%,均超过国家相关标准。故下文开展斜切(30°)等截面扩大段式缓冲结构对微气压波的缓解研究,分析其长度和开孔数对微气压波的影响。

表2 不同隧道长度下测点1微气压波幅值及增长率Table 2 Amplitude and growth rate of the micro-pressure wave at measurement point 1 for different tunnel lengths
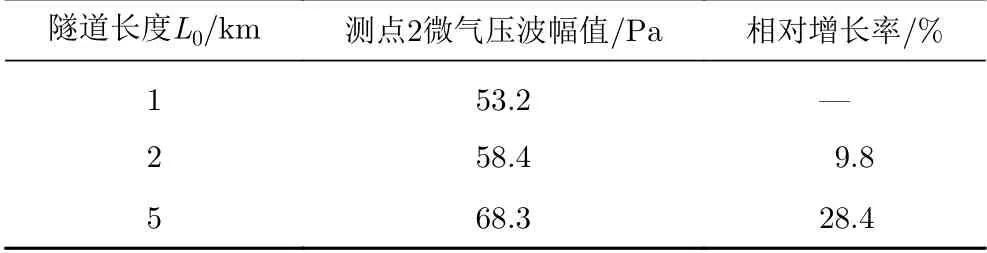
表3 不同隧道长度下测点2微气压波幅值及相对增长率Table 3 Amplitude and growth rate of the micro-pressure wave at measurement point 2 for different tunnel lengths
3.2 带斜切(30°)的缓冲结构长度对微气压波的影响
图14(a、b)为高速列车以时速400 km/h通过不同长度的缓冲结构隧道(隧道长1 km)时,测点1和测点2的微气压波随时间的变化曲线,其中缓冲结构长度L分别为68.56 m、78.56 m、88.56 m、98.56 m,且选用无缓冲结构的工况作为对比。可以发现与无缓冲结构相比,每个长度的缓冲结构对微气压波都有较好的缓解效果,最优缓冲结构长度为88.56 m。表4和表5分别为测点1和测点2在不同长度缓冲结构下微气压波幅值及其相对无缓冲结构的缓解率,可见缓冲结构长88.56 m时,测点1和测点2的微气压波幅值的最大缓解率分别为59.2%和56.0%。图15为两个测点微气压波幅值随缓冲结构长度变化的曲线,可以看出微气压波幅值随着缓冲结构长度的增加先减小后又略微增大。
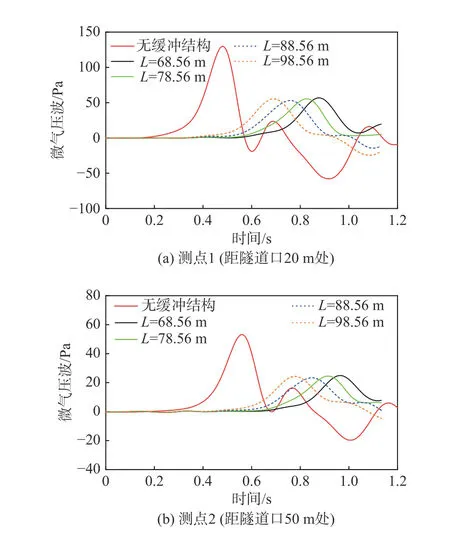
图14 不同缓冲结构长度下隧道口微气压波曲线图Fig. 14 Micro-pressure wave curves at the tunnel exit for different tunnel-hood lengths
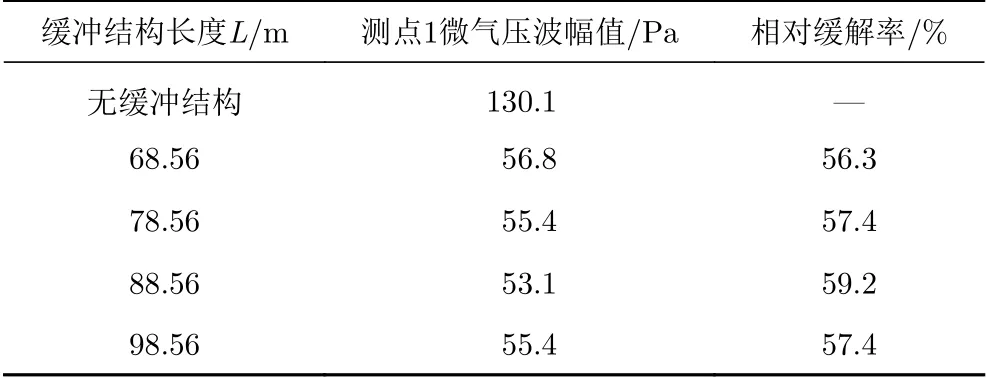
表4 不同缓冲结构长度下测点1微气压波幅值及相对缓解率Table 4 Amplitude and alleviative rate of the micro-pressure wave at measurement point 1 for different tunnel-hood lengths
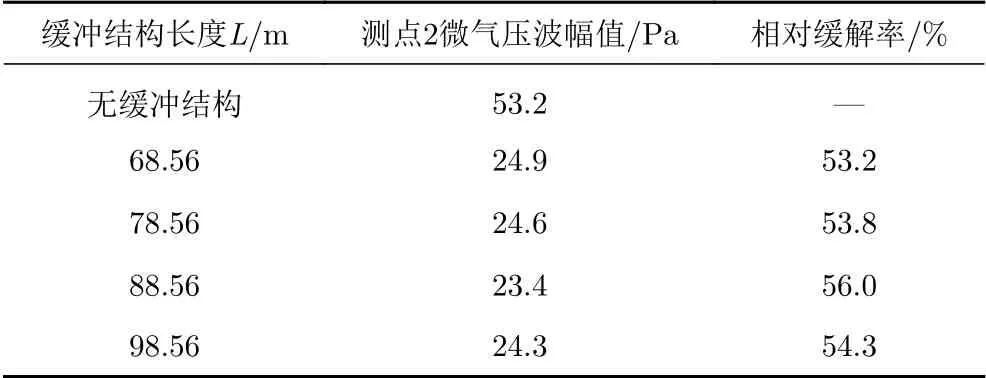
表5 不同缓冲结构长度下测点2微气压波幅值及相对缓解率Table 5 Amplitude and alleviative rate of the micro-pressure wave at measurement point 2 for different tunnel-hood lengths
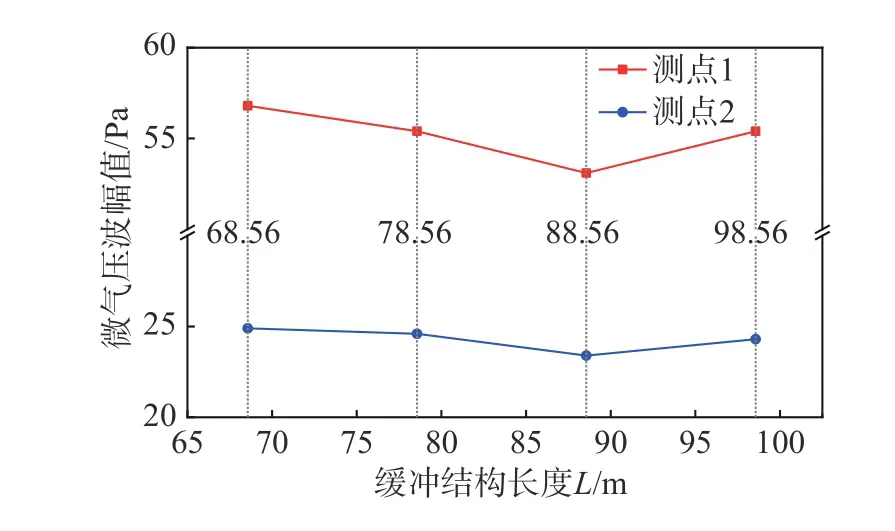
图15 微气压波幅值随缓冲结构长度的变化Fig. 15 Variation of the amplitude of the micro-pressure wave with the tunnel-hood length
分析其原因,在周丹[18]的研究中可知:当缓冲结构长度在一定倍数的隧道等效水力直径之内时,微气压波幅值随缓冲结构长度的增加而减小;当其长度超过一定倍数的隧道等效水力直径后,微气压波基本不变,此长度定为临界长度Lh。其研究也发现了不同的车速对应不同的Lh,当缓冲结构长度超过各自速度对应的Lh时,速度越大,在该长度之后对应的微气压波增大的越明显,这与本文结果相符。在最优长度的缓冲结构下(88.56 m),测点1和测点2的微气压波幅值分别为53.1 Pa和23.4 Pa,仍不满足国家标准,故需进一步对微气压波进行缓解。
3.3 缓冲结构开孔个数对微气压波的影响
由上文知隧道长1 km时,不开口缓冲结构长为88.56 m对微气压波缓解效果最好,但仍不能达到标准要求,所以下文研究隧道长1 km时,斜切(30°)缓冲结构(L= 88.56 m)的开孔率对微气压波的影响,以寻求更好的缓解效果。
图16为高速列车以时速400 km通过不同开孔数的缓冲结构隧道时,测点1和测点2的微气压波随时间的变化曲线,可以发现相对于0开孔的缓冲结构,开1孔和开2孔可以使微气压波幅值减小,开3、4、5孔会使微气压波幅值增大,且微气压波曲线中的第一个峰值随着开孔数的增加向后移动。这是因为开孔的位置是沿着列车运行方向纵向排列的,随着列车的运行,开孔处发生泄气,延长了初始压缩波形成的时间,从而引起微气压波达到幅值的滞后。
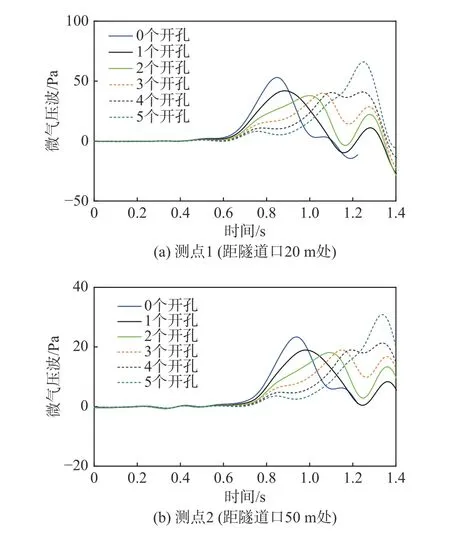
图16 不同开口数的缓冲结构下微气压波曲线图Fig. 16 Micro-pressure wave curves for tunnel-hoods with different numbers of opening holes
表6和表7分别为测点1和测点2在不同开孔数的缓冲结构下微气压波幅值和相对无缓冲结构的缓解率。可见测点1和测点2具有相同的变化规律:微气压波幅值随开孔数的增加先减小后增大,在开孔数为2时微气压波幅值最小,这与Liu[35]等发现的“微气压波幅值随缓冲结构开孔率的增加先减小后增大”的规律基本相符,但其研究的最优开孔率为0.018,本文两个开孔对应的开孔率为0.0213,这主要是因为本研究的车速为400 km/h,缓冲结构带有斜切,且缓冲结构长度面积、隧道长度面积等都与文献[35]研究的不同,但整体变化规律是一致的。下面分析此变化规律的原因:孔①②③④⑤沿缓冲结构长度方向纵向排列,当开孔数较少时(2个开孔以内),列车进入缓冲结构被压缩的空气会在开孔处发生泄气,延长了初始压缩波最大值形成的时间,从而初始压缩波的最大压力梯度下降,且2个开孔时泄气量大于1个开孔,所以2开孔的初始压缩波最大压力梯度小于1开孔;当开孔数大于2时,因为①②开孔已经分散了大部分压缩气体,随着列车的运动,在开孔处会有进气和出气的复合作用,且在开孔处和扩大段与隧道交接处产生的复杂小波会相互叠加,在上述因素的共同作用下,相对于2开孔时,初始压缩波的最大压力梯度会增大。测点1和测点2微气压波幅值分别为37.9 Pa和18.1 Pa,相对无缓冲结构时的缓解率分别为70.9%和66.0%,都已满足标准要求。
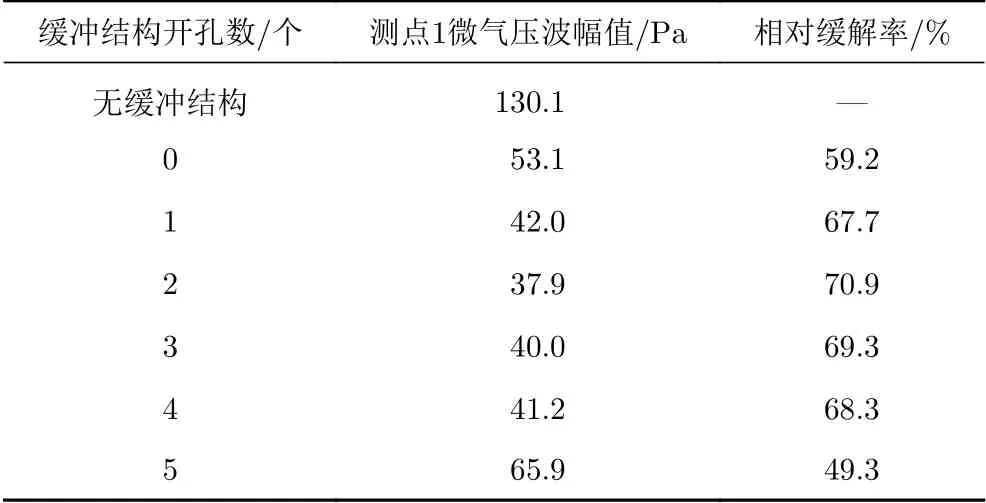
表6 不同开孔数的缓冲结构下测点1微气压波幅值及相对缓解率Table 6 Amplitude and alleviative rate of the micro-pressure wave at measurement point 1 for tunnel-hoods with different number of opening holes

表7 不同开孔数的缓冲结构下测点2微气压波幅值及相对缓解率Table 7 Amplitude and alleviative rate of the micro-pressure wave at measurement point 2 for tunnel-hoods with different numbers of opening holes
图17(a)为采用斜切30°长88.56 m开2孔的等截面扩大段缓冲结构,隧道长分别为1 km、2 km、5 km时压缩波变化的曲线,图17(b)为对应压力梯度的变化。可以看出,压力幅值和压力梯度的幅值都受到了隧道在长度方向的激化,随隧道长度的增加而增加,这与3.1节中得到的微气压波受隧道长度的激化的规律一致。另外,Yamamoto[36]利用远场和低频的近似方法得到了微气压波幅值与压缩波的最大压力梯度成正比的关系,所以微气压波幅值与压力梯度幅值变化规律具有一致性。同时,本文旨在研究400 km时速下的隧道口微气压波的缓解措施,以使微气压波达到相关标准,所以直接监测隧道口的微气压波是可取的。
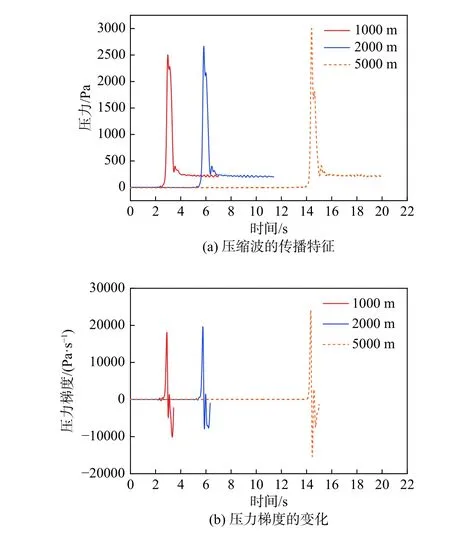
图17 不同隧道长度下压缩波及压力梯度的变化Fig. 17 Variation of the compression wave and pressure gradient for different tunnel lengths
图18为隧道长1 km、2 km、5 km时,采用斜切30°长88.56 m开2孔的等截面扩大段缓冲结构,在测点1和测点2的微气压波幅值的曲线,表8是对应的微气压波幅值。可见采用上述缓冲结构可将长1 km、2 km、5 km隧道的微气压波幅值都降到标准以下。故本文提出的斜切角为30°、扩大段长度为88.56 m、开2孔的缓冲结构能使长为5 km及以下长度的时速400 km高速铁路隧道口微气压波缓解达到国家相关标准。
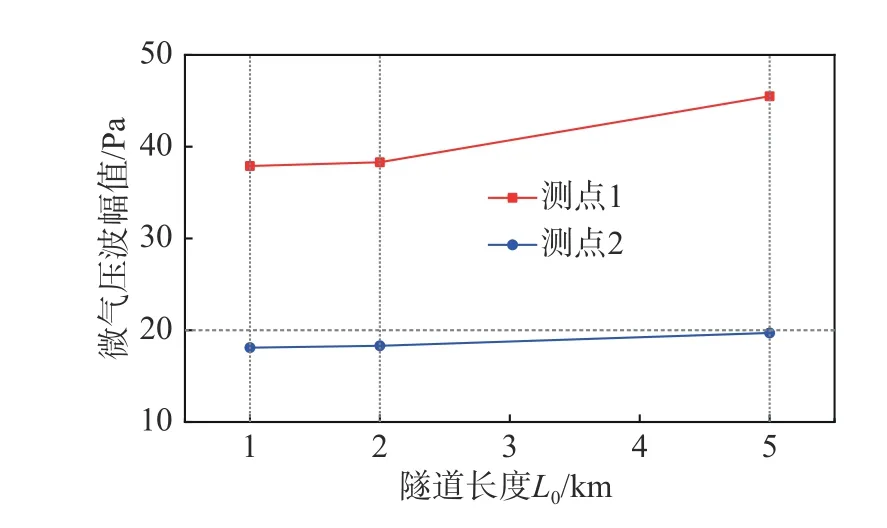
图18 缓冲结构开2孔时微气压波幅值随隧道长度的变化Fig. 18 Variation of the amplitude of the micro-pressure wave with the tunnel length for the tunnel-hood with 2 opening holes
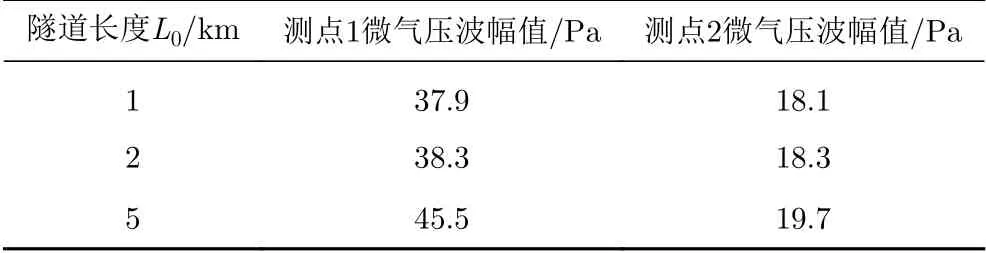
表8 缓冲结构开2孔时不同隧道长度的微气压波幅值Table 8 Amplitude of the micro-pressure wave for different tunnel lengths with 2 opening holes on the tunnel-hood
4 结论
本文通过数值模拟和动模型实验,对时速400 km高速铁路隧道口微气压波进行分析,研究隧道长度、斜切角为30°的缓冲结构长度和开孔数对微气压波的影响。主要结论如下:
1)隧道长度在5 km以内时,微气压波幅值随着隧道长度的增加而增大,其中隧道长5 km与1 km相比,在距隧道口20 m和50 m处微气压波幅值分别增大了27.4%和28.4%;
2)微气压波幅值随着缓冲结构长度的增加先减小后又增大,随着缓冲结构开孔数的增加微气压波幅值先减小后增大,存在最优的缓冲结构长度和开孔数,最优长度为88.56 m,最优开孔数为2开孔;
3)最优长度与最优开孔数组合的缓冲结构,能使隧道长为1 km的微气压波幅值在距隧道口20 m和50 m处分别缓解70.9%和66.0%;并能使长为5 km及以下长度的时速400 km高速铁路隧道口微气压波缓解达到国家相关标准。
