基于OPTICS聚类算法的流场结构特征分析方法
2021-11-13辛大波欧进萍
王 锐,辛大波,欧进萍
(1. 哈尔滨工业大学 土木工程学院,哈尔滨 150090;2. 东北林业大学 土木工程学院,哈尔滨 150040)
0 引言
长大跨度桥梁、远距离大跨度的输电塔线、高耸通讯塔桅等基础设施,分别构成了交通网络、能源网络和通讯网络中的关键节点,是我国乃至世界各国经济社会发展所需要的基础设施工程。这些工程结构往往具备长、柔的特征,对风荷载敏感,易产生显著的风致静力和振动响应[1-3]。因此,对长、柔结构物的风工程问题进行研究,对于提高结构抗风能力,保障基础设施网络的安全性、可靠性和鲁棒性具有十分重要的意义。
流场结构特征分析是风工程研究中的重要内容,是揭示结构物周围的流场结构,归纳流动规律,分析结构的风荷载成因与控制方法的必要途径。一般结构物附近的流场可以由基于计算流体动力学(CFD)的数值模拟手段获得[4-7]。近年来,随着如粒子图像测速(PIV)这样的流场可视化技术的发展,利用风洞试验也可以获取结构周围流场[8-9]。
流场数据一般包含流场区域中各点对应的速度、涡量、湍动能等数据,是一种典型的高维数据。对流场数据的分析要依赖于各种各样的降阶模型[10]。本征正交分解(POD)是一种在流场动力分析中常用的降阶方法,其假设每一个流场样本可以视为不同流场模态的线性组合,并通过对特征值问题的求解,获取各流场模态的统计显著程度[11-12]。动模态分解(DMD)则假设每一个流场样本可由上一时刻的流场样本通过线性映射矩阵获得。相对于POD,DMD的系统矩阵中囊括了更多的时序信息,从而能够获取更准确的模态频率[13-14]。无论是POD还是DMD,都需要依赖于一些动力学假设,但这些假设相对于湍流这样复杂的动力学问题过于简单。因此,有必要研究不依赖于动力学假设的流场结构特征分析方法。
Kaiser等提出将聚类分析方法引入到流场分析技术中[10]。聚类分析是一种由数据驱动的机器学习方法,用于将样本数据分组为不同类,每一类中的样本具有一定程度的相似性[10]。聚类分析完全依托于流场数据,不依赖于动力学假设,因此在流场分析的应用上更有前途。目前有一些聚类分析在PIV试验[15]和数值模拟[10,16]结果分析的应用,在对流场结构特征的分析中取得了较好的结果。值得注意的是,上述研究中普遍采用的是聚类分析中的k-means算法。k-means算法是一种基于平均值的聚类算法,即:在所有数据中随机选取k个作为初始聚类中心,通过对样本和聚类中心欧氏距离的计算和比较,将样本归于距离最近的聚类中心;分类完成后以各类样本平均值作为新的聚类中心替换初始聚类中心,重复上述计算直至本次迭代得到的新聚类中心与本次迭代的初始聚类中心重合[17]。这样的算法就意味着,k值的选取不唯一,计算得到的结果不唯一,且最终得到的分类在样本中均匀分布。对于识别流场的结构特征,k-means算法稍显粗糙。
考虑到聚类算法在流场结构特征分析中的优越性和目前常用的k-means方法的一些缺陷,本文将关注于寻找一种算法以改善基于k-means算法的流场聚类分析方法。本文选取了一种基于密度的聚类算法OPTICS (Ordering Points To Identify the Clustering Structure),并通过引入相关距离的概念替换欧氏距离,形成了基于相关距离的OPTICS算法。利用基于大涡模拟(LES)的计算流体动力学(CFD)数值模拟,获取了经典圆柱绕流尾流中的顺流向涡涡量场样本。以识别顺流向涡脱落状态和其A模式分布的展向间距为目标,检验基于相关距离的OPTICS算法的有效性,并分别与原始的OPTICS算法和k-means算法对比。结果表明,基于相关距离的OPTICS算法是一种有效的用于流场结构特征分析的聚类分析算法。
1 基于OPTICS算法的流场聚类分析
1.1 OPTICS聚类算法的基本概念
OPTICS是一种基于密度的聚类分析算法,即以数据点的空间密度作为判别标准,将每个高密度区域中的数据点作为一类。相对于k-means算法需要由人工设置初始聚类数目且聚类结果不唯一,OPTICS算法能够基于初始参数识别样本中的高密度数据点集,从而相对客观地找到样本中的高密度区域,给出符合样本分布规律的聚类。对于确定的样本,其数据分布可以唯一确定,因此基于密度判别的OPTICS算法可以获得相对稳定的聚类中心。针对于流场结构特征分析,当选取合理的相似度指标,OPTICS算法识别出的高密度数据集即意味着该数据集中的流场样本高度相似,也即具备同一特征。那么通过OPTICS算法的聚类,就可以相对客观地判别流场样本所包含的结构特征。
假设已经获得了n组流场数据X= [x1,x2,···,xi,··· ,xn],其中xi代表第i个流场数据。每个流场数据为一个m维向量,代表了流场中的m个测量值,也代表了m维欧氏空间中的一个点。OPTICS算法的关键概念,是对每一个xi建立一个半径为ε的邻域Nε(xi),且应有不少于MinPts个数据点在该领域中。据此我们可以引入以下概念[18-19]:
1)密度直达:如果X中的两个流场xi、xj(i≠j)满足:xi∈Nε(xj)且card(Nε(xj)) ≥MinPts,则称xi可由xj密度直达。其中,card(Nε(xj))表示集合Nε(xj)包含的元素数,card(Nε(xj)) ≥MinPts的条件被称作核心对象条件,xj可以被称为核心对象,其他流场数据只能由核心对象密度直达。
2)密度可达:如果存在一系列X中的流场数据xr、xr+1、···、xr+s,当i∈[r,r+s− 1]时xi可由xi+1密度直达,则称xr可由xr+s密度可达。
3)密度相连:如果X中的流场数据xi和xj(i≠j)均可由X中的另一流场数据xk(k≠i且k≠j)密度可达,则称xi和xj密度相连。
4)类:类是聚类分析得到的结果,一类流场数据Y是X的一个非空子集,且满足以下两点:①对任意xi、xj(i≠j)∈X,如果xj∈Y且xi可由xj密度可达,则xi∈Y;②对任意xi、xj(i≠j)∈X,xi和xj密度相连。如果有些X中的流场数据没有被分在任何一类中,则称之为噪声。
5)核心距离:从xi到其邻域Nε(xi)中某一数据点,使xi成为核心对象的最小距离,可以数学表达为:

式中:dc(xi)是xi的核心距离;为在xi的邻域Nε(xi)中,距离xi第MinPts近的流场数据;d(xi,表示xi和之间的距离。
6)可达距离:对xi、xj(i≠j)∈X,xi关于xj的可达距离可以定义为:

其含义是,使xi可由xj密度直达和xj为一个核心对象同时成立的最小距离。
1.2 OPTICS聚类算法用于流场聚类的步骤
执行OPTICS聚类算法,需要首先输入流场数据序列X,其次是邻域半径ε和邻域集合最小元素数MinPts,然后执行以下步骤[18]:
1)在X中随机选择一组数据xi作为当前对象(执行中往往选择第一组数据),将其标记为已处理,并描绘在决策图顺序轴的第一个位置,其对应的可达距离是无意义的,一般在程序中赋予一个较大值。
2)计算X中所有其他流场数据关于当前对象的可达距离。
3)找到关于当前对象可达距离最小的一组数据,用该组数据替换当前对象并标记为已处理,将该组数据按处理顺序和可达距离描绘在决策图对应位置。
4)依次计算未处理数据关于当前对象的可达距离,如果这些可达距离中存在小于步骤3)中计算出的可达距离,则将其对应的数据替换为当前对象;否则保持原有当前对象不变。
5)重复步骤3)、4)直至X中所有数据处理完毕。
OPTICS算法得到的结果用决策图表示。如图1所示,其横轴表示流场数据的处理顺序,其纵轴表示该流场数据关于处理时当前对象的可达距离。通过与已经设置好的邻域半径ε对比,若可达距离dr<ε,则该可达距离有意义,其对应的流场数据被聚为一类。图1的决策图表示该组数据被聚为三类。

图1 OPTICS算法的决策图示意Fig. 1 An example of the reachability-plot of OPTICS
2 基于相关距离的OPTICS聚类算法
2.1 基于欧氏距离OPTICS聚类算法的缺陷
OPTICS聚类算法依赖于邻域半径、核心距离和可达距离等距离概念,基于这些距离来判别数据的分布密度。传统的OPTICS算法往往采用欧氏距离[18-19],即将流场数据X中的xi和xj视为m维欧式空间中的两个点,将xi和xj中的元素作为其在m维欧式空间中各个维度上的坐标,计算两点间的几何间距。采用欧氏距离定义清晰,计算方便,但却忽略了流场数据的空间分布特性,割裂了一个流场数据内各个元素间的联系,这对于识别流场的模式和结构特征是不利的。
2.2 常用相似度指标在流场结构特征识别中的适用性
常见的衡量高维数组间距离的相似度指标包括欧氏距离、切比雪夫距离、闵可夫斯基距离、马氏距离、相关系数、夹角余弦等,其定义如表1所示。根据这些指标的定义,可以将其简单分为两类,其一是以空间坐标间距(ai -bi)为核心的距离概念,包括欧氏距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离和马氏距离;其二则是以统计相关性为核心的相关系数概念,包括夹角余弦、Pearson相关系数和Spearman相关系数。

表1 衡量高维数组间相似程度的常见相似度指标Table 1 Common indexes for evaluating the similarity among high-dimensional arrays
流场样本往往是一套以空间坐标标记的物理量,该物理量可以是流速、压力、涡量、湍流度、或湍动能等。在对流场结构特征进行识别和分析时,需要将流场样本的空间坐标按一定规律映射于一个一维数组的元素角标,而该一维数组中的元素为各角标对应的物理量,从而将原始的流场样本组织为高维数组。流场的结构特征主要体现在物理量的空间分布,其含义既包括物理量本身的大小,也包括特定大小的物理量出现的空间位置。例如根据流速和涡量的空间分布,可以识别流场中旋涡的形状、位置与强度;根据钝体边界层中压力的空间分布,可以识别到钝体绕流的分离点。因此,识别流场的结构特征,对流场样本进行相似度的度量,既需要关注物理量本身的大小,即流场样本数组中的元素大小;也需要关注物理量的空间坐标,即流场样本数组中的元素角标。
为了说明基于统计相关性的相似度指标在流场分析中的优势,这里举例如下。假设存在三组简单的流 场 样 本:a= [1,0,1]T,b= [0,2,0]T,c= [3,0,3]T。a和c的元素大小不同,但其中较大值的元素出现在相同的位置,即元素的分布规律相似,这代表着这两个样本具有相似的流场结构;a和b中较大值的元素出现在不同位置,这代表着这两个样本的流场结构显然不同。按上述指标计算a、b之间和a、c之间的距离,结果如表2所示。显然,基于空间坐标间距(ai-bi)的距离指标普遍没能识别出a和c之间具有更加相似的物理量分布,而基于统计相关性的夹角余弦、Pearson相关系数和Spearman相关系数均体现出了这一点。

表2 基于不同相似度指标计算的a、b、c之间的距离Table 2 Distances among a,b and c calculated by different similarity indexes
当对流场样本这样的高维数组进行相似度度量时,以空间坐标间距(ai-bi)为核心的距离指标,更加注重元素大小的衡量,而忽略各个维度间的联系;以统计相关性为核心的相关系数指标则偏重于关注对元素分布的衡量,这一特性对于识别流场物理量的空间分布更加有利。具体分析各个指标,其中欧氏距离、曼哈顿距离和切比雪夫距离分别是闵可夫斯基距离在p= 2、p= 1和p趋于正无穷时的特殊情况,这一类的指标显然割裂了不同维度的元素间的联系。马氏距离的定义式中包含了样本的协方差矩阵的逆矩阵,这就要求样本的协方差矩阵满秩,对于流场样本这种维度往往在104以上数量级而样本数相对少的样本矩阵,其协方差矩阵通常不能满足满秩的条件。如果采用POD方法对流场样本降维处理,又会引入线性系统的假设。所以马氏距离在流场结构特征识别中只能有限应用于样本量不少于样本维度的情况。夹角余弦和Pearson相关系数形式接近,当样本A和B的均值均为0时,Pearson相关系数就可以写作夹角余弦的形式,也即Pearson相关系数是排除了样本元素均值影响的夹角余弦。当样本元素的均值存在较大波动,基于夹角余弦的相似度衡量可能受到均值的影响。Spearman相关系数基于样本A和B的秩次获得,也就是忽略样本中元素的具体数值,而利用其在所有元素中的大小排序进行计算。Spearman相关系数完全忽略了样本元素的具体数值,对于流场这种包含同一物理量的样本集并不适用。综上所述,Pearson相关系数相对更适合于作为衡量样本相似度指标,应用于基于OPTICS聚类算法的流场结构特征识别。
2.3 基于相关距离的OPTICS聚类算法
基于对流场样本数据特征和各类距离指标的分析,本文引入基于Pearson相关系数的相关距离的概念,并用相关距离替换了传统OPTICS算法采用的欧氏距离,以使OPTICS聚类算法更加适用于识别流场结构特征。首先,Pearson相关系数的概念可以按下式定义:
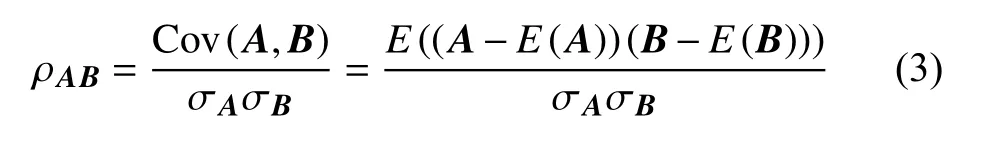
式中:A、B表示两组相同维度的向量;ρAB为向量A、B的相关系数;Cov(A,B)为A,B的协方差;E(A)和E(B)表示A和B的期望;σA和σB表示A和B的标准差。根据Pearson相关系数可以定义向量A、B的相关距离如下式:

式中:dAB表示向量A、B的相关距离。相关距离越小,表明向量A和B越相似;反之则表明向量A和B差异越大。
3 典型圆柱绕流场结构分析实例
3.1 流场结构特征识别对象
圆柱绕流是一种经典的钝体绕流现象,实际工程结构中具有大量的圆柱形弹性结构,例如大跨桥梁的斜拉索、吊索、长大跨度输电线、海洋管道等。这些结构极易受到来流作用而发生流致响应,导致结构的疲劳损伤甚至破坏。对圆柱形结构的三维绕流场进行流场结构分析,对于研究其流致响应机制,开发流动控制方法具有重要的作用。因此,本文以识别圆柱尾流中顺流向涡的A模式[20]为目标,通过CFD数值计算手段获取流场分析对象,用来说明基于相关距离的OPTICS聚类算法的优越性。数值模拟对象为一个沉浸于均匀流中且与来流方向正交的静止圆柱体,长l= 0.2 m,直径d= 0.01 m,长细比20∶1,其轴线与z轴重合。计算域为一个高20d,半径为35d,轴线与圆柱模型轴线重合的圆柱体,如图2所示。计算域各边界条件如图2所示,来流风是U= 0.35 m/s的均匀流,从入口沿x轴方向进入,从出口自由流出。计算的雷诺数Re约为240。
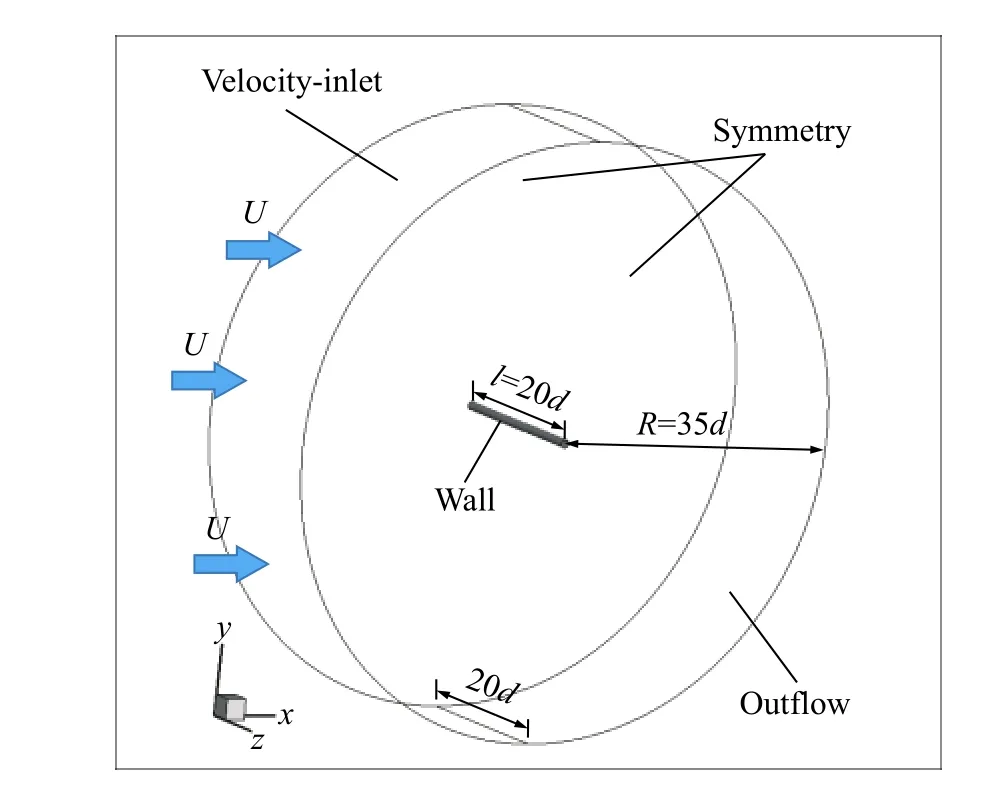
图2 计算域几何特征与边界条件Fig. 2 Geometry features and boundary conditions of the calculation domain
计算域采用结构化网格划分,共计包含2187416个六面体网格。计算域被沿圆柱轴线等分为67层,每层网格如图3所示。其中靠近圆柱壁面的网格约为0.1 mm×0.1 mm的正方形,沿周向等分,沿径向按扩散率1.05向外侧扩大。圆柱模型表面的壁面y+如图4所示,模型表面各点的y+均小于0.5,说明第一层网格足够精细以满足计算需求。计算利用商业软件Fluent执行瞬态模拟,采用三维大涡模拟(LES),亚尺度模型选用WALE。动量按二阶迎风格式离散,压力和瞬态方程采用二阶格式离散。计算时间步长为5×10−5s。

图3 网格划分示意Fig. 3 A schematic of the mesh

图4 圆柱壁面y+Fig. 4 y+ on the surface of the circular cylinder
为了验证数值计算结果的准确性,本文对圆柱模型气动力系数的统计值和斯托拉哈数(St)与相关参考文献提供的其他试验结果的拟合值进行了对比,对比结果如表3所示。数值计算获得的圆柱阻力系数时均值与试验拟合结果的偏差均小于5%,数值计算的St与试验拟合结果的偏差约为5%,数值计算结果可信。
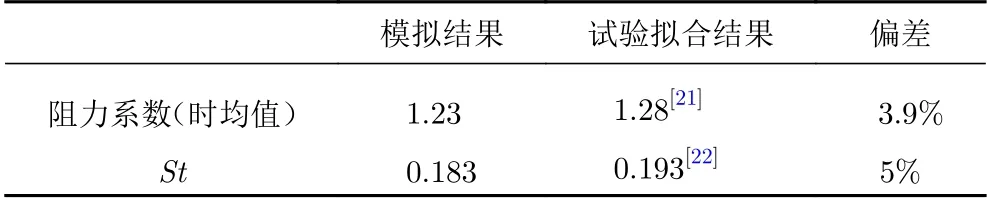
表3 气动力系数验证Table 3 The comparison of the numerical and experimental aerodynamic forces
流场分析的识别目标是在x= 2.5d切面上,识别圆柱尾流中顺流向涡的A模式旋涡脱落的两种状态与样本中包含的两种展向间距(如图5所示)。顺流向涡的A模式是指在雷诺数超过190左右时,圆柱尾流中除卡门涡之外,出现了旋转轴沿来流方向的旋涡。其出现方式为一系列沿展向按间距约4d排列的方向相反的旋涡对,与卡门涡呈相同频率脱落,并且每半个卡门涡脱周期发生一次旋转方向的变化。由于数值计算存在的数值误差和尾流中顺流向涡本身的不稳定性,相当于流场本身存在不属于标准模式的噪声。有效的流场分析方法应当能识别到x= 2.5d切面上,顺流向涡的展向分布间距和旋涡脱落的两个状态,并排除噪声流场的干扰。流场样本共计按时间步长0.005 s采样2000份,从流动的第4 s采样至第14 s。样本数据为x= 2.5d切面上的x方向涡量场。

图5 圆柱尾流中顺流向涡的旋涡脱落与A模式示意Fig. 5 The vortex shedding and the A-mode of the streamwise vortices in a circular cylinder wake flow
3.2 基于k-means聚类算法的流场结构特征识别
k-means聚类算法中,聚类数目N作为初始参数输入,需要利用总方差的概念对初始聚类数目N进行判别。对于每一类,可以获得各样本围绕该聚类中心的统计方差,各个类的方差之和即为总方差。理论上当N= 1时,总方差达到最大;当N与样本总数n相同时,总方差为0,最优的聚类数目N应当在较小的总方差和较少的聚类数目中取得平衡。一般地,最佳聚类数目可以经由总方差的“肘形判据”获取[10]。本例中尝试将初始聚类数目N设置在2~12范围内,获得总方差如图6所示。总方差随着聚类数目N的增长单调下降,斜率逐渐减小;但是曲线上并不能明显找到“肘部”,“肘形判据”并不能明确给出最合理的聚类数目。
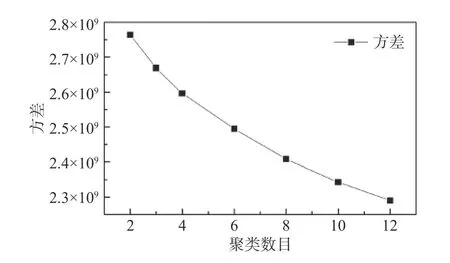
图6 k-means算法的方差与初始聚类设置的关系Fig. 6 The number of initial clusters as a function of the variances of the k-means algorithm
图7展示了聚类数目分别为2、4、6和8时的流场分析结果,每一类流场的分析结果为各类流场的聚类中心。当N= 2时,两类流场分别对应顺流向涡脱落的两个状态,可以认为捕捉到了顺流向涡脱落;但是A模式应当具有的约4d展向间距的顺流向旋涡对在这两个结果中体现不明显,两种展向间距没能得到区分。当N> 2时,顺流向涡的A模式在部分类别中得到体现,但由于分类增多,出现了两个问题:其一,顺流向涡的脱落状态不能被这些类明确;其二,当N=8时,出现了类似的多个聚类,即过度分类。
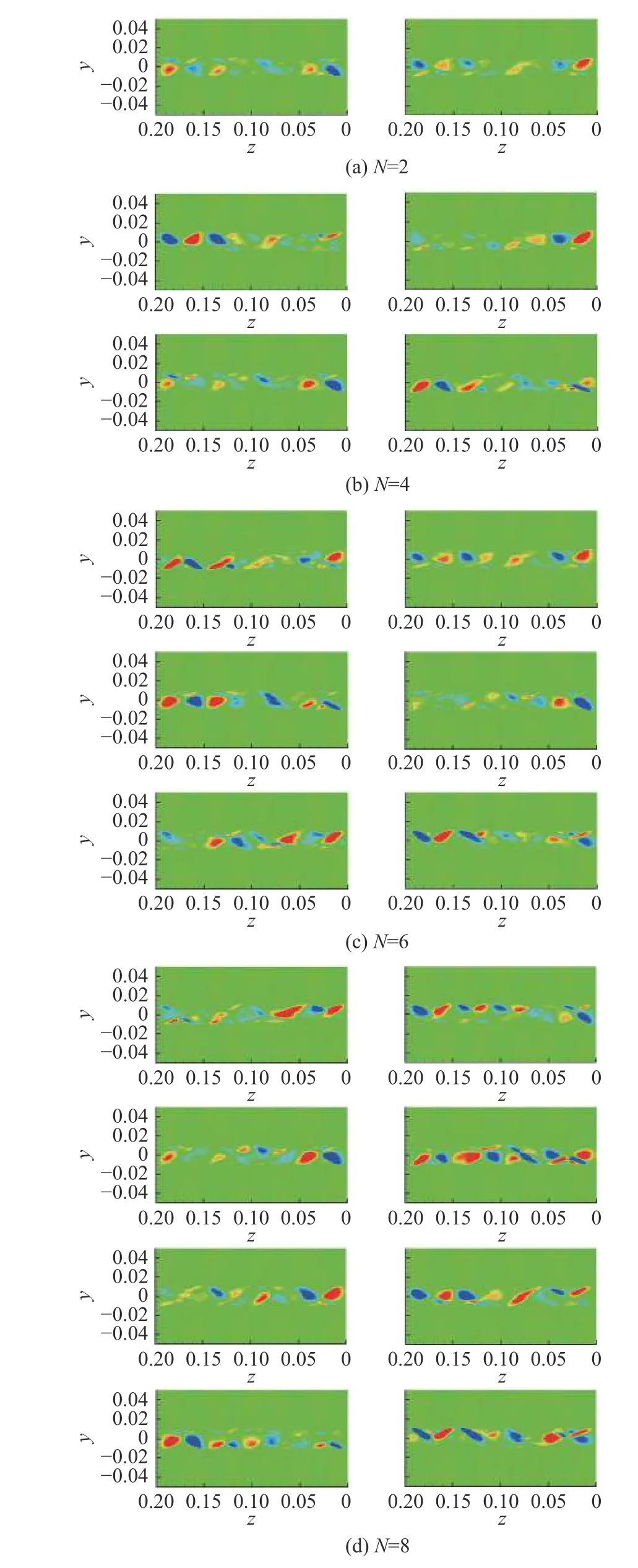
图7 k-means算法的流场结构特征识别结果Fig. 7 The identified flow structures by the k-means algorithm
总的来说,k-means算法难以在识别顺流向涡脱落和顺流向涡展向间距之间取得平衡。另外k-means算法的输出结果严重依赖输入的初始聚类数目N,且难以找到相对最优的N。k-means算法在计算中随机选取初始聚类中心,所以其聚类结果存在随机性,同一组样本数据多次聚类的结果并不一致。
3.3 基于原始OPTICS算法的流场结构特征识别
OPTICS算法不需要像k-means算法一样设置初始聚类数目,其初始参数是ε邻域Nε(xi)中最小点数MinPts和邻域半径ε,而最终的聚类结果由决策图获得。基于OPTICS算法的流场分析结果如图8所示,共计采用60~200间的六组MinPts,Ni表示第i类中的样本数量,每个流场的聚类结果由各类中流场样本的平均场表示。图8(a)显示,当MinPts= 60,令ε= 1010,可以在决策图中找到两个聚类,分别对应顺流向涡脱落的两个状态,且顺流向涡的A模式比较明显。但是仅识别到顺流向涡对的4d展向间距,5d的展向间距没能在聚类结果中体现;且由于MinPts取值较小,造成聚类中样本数量偏小,大量的样本被识别为了噪声。图8(b~f)给出了MinPts≥80的5种情况,其决策图中均只能找到一个聚类,这一类的聚类中心既不能体现顺流向涡的脱落,也不能体现A模式涡对的展向分布。也就是说,MinPts≥80时,OPTICS算法不能够识别出顺流向涡涡量场的状态。
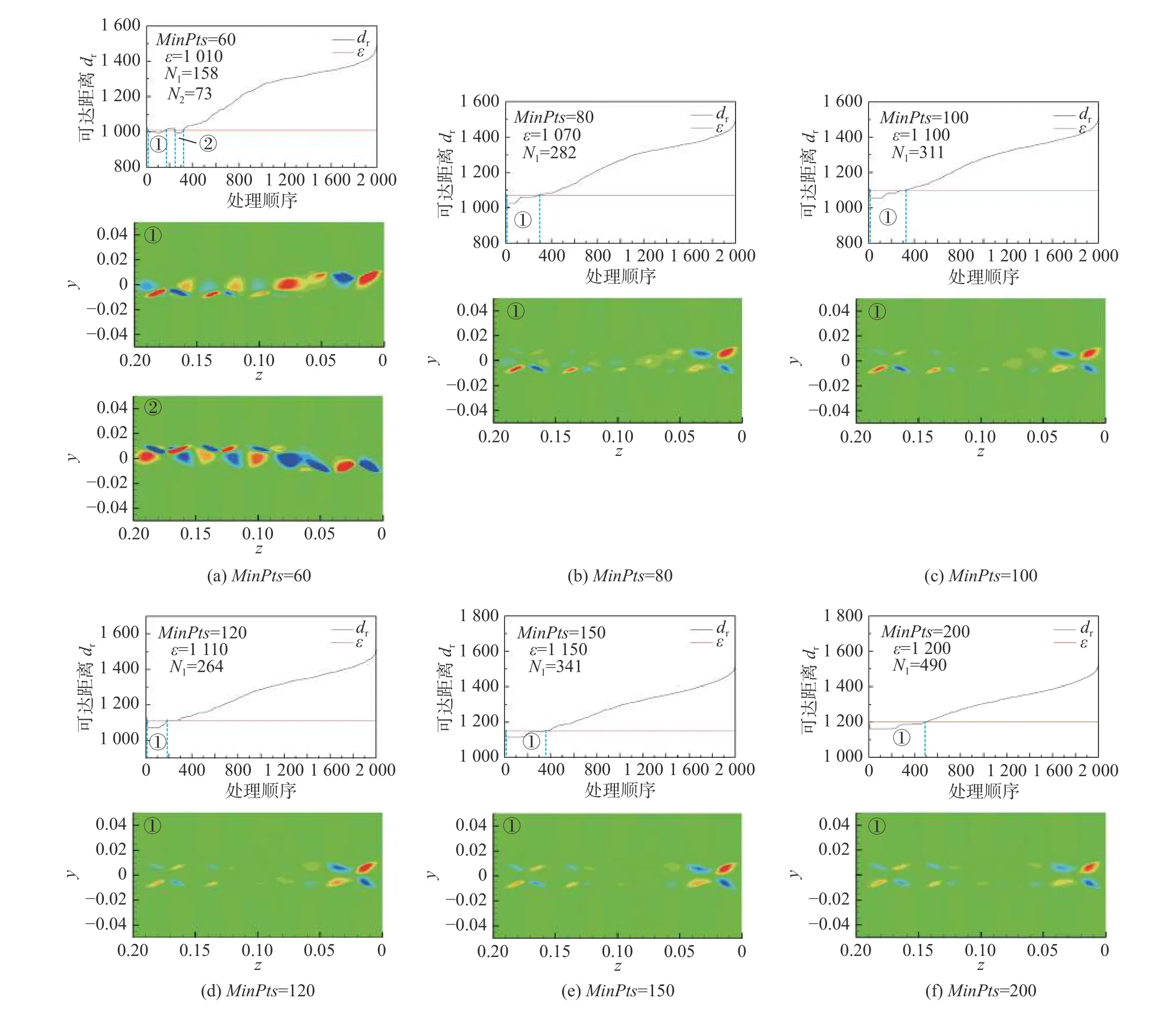
图8 原始OPTICS算法的决策图与聚类中心Fig. 8 The reachability-plots and cluster centers of the original OPTICS algorithm
3.4 基于闵可夫斯基距离的OPTICS算法的流场结构特征识别
闵可夫斯基距离是一种典型的以空间坐标间距(ai-bi)为核心的距离指标,原始OPTICS算法采用的欧氏距离即对应于p= 2时的闵可夫斯基距离。基于闵可夫斯基距离的OPTICS算法的流场结构特征识别结果与原始的基于欧氏距离的OPTICS算法类似,图9列出了p= 5时的流场分析的决策图与聚类中心,可见MinPts取值在60~120之间时,选取适宜的邻域半径ε,都可以得到分别对应于顺流向涡脱落的两个状态的两个聚类中心。相对于p= 2时的聚类结果,能够识别旋涡脱落的MinPts取值范围大幅增大,但仍然没能识别出5d的顺流向涡展向间距。

图9 基于闵可夫斯基距离(p = 5) OPTICS算法的决策图与聚类中心Fig. 9 The reachability-plots and cluster centers of the OPTICS algorithm based on the Minkowski distance (p = 5)
参数p取值对闵可夫斯基距离的定义十分重要,对基于闵可夫斯基距离的OPTICS算法的流场结构识别结果也有影响。表4列出了参数p的取值对聚类中心数目的影响。当利用基于闵可夫斯基距离的OPTICS算法对顺流向涡结构进行识别时,若识别出两个聚类中心,其结果往往对应于顺流向涡脱落的两个状态;若识别出一个聚类中心,则意味着没能区分出任何结构特征。随着参数p取值的增加,能够识别旋涡脱落特征的MinPts取值范围逐渐增大。但当采用切比雪夫距离,当MinPts= 60时出现了过度分类,在识别出顺流向涡脱落特征的同时,将顺流向涡脱落的其中一个状态识别成两种状态;而MinPts≥80时无法区分出任何流场结构特征。需要指出的是,当聚类中心个数相同时,基于闵可夫斯基距离的OPTICS算法获取的决策图图形类似,聚类中样本数量普遍偏少,大量的样本被识别成了噪声。

表4 p的取值对聚类数目的影响Table 4 The effects of p on the number of clustering centers
3.5 基于相关距离的OPTICS算法的流场结构特征识别
基于相关距离的OPTICS算法的初始参数与原始OPTICS算法一致,区别仅在于其邻域半径ε用相关距离表达而非欧氏距离。相关距离可以根据夹角余弦、Pearson相关系数或者Spearman相关系数构造,本节将比较这些不同的相似度指标对基于相关距离的OPTICS算法的影响。
图10列出了基于Pearson相关距离的OPTICS算法获得的决策图和对应的聚类中心。对于全部的MinPts的取值,均可以找到适宜的邻域半径ε,对涡量场样本的特征实施聚类。当MinPts取60和80时,能够找到6个明显的聚类中心,其中1~4号聚类对应于间距约为5d的顺流向涡对的脱落状态,由于z= 0.08 m处涡核形状存在差异,出现了过度分类的情况;5~6号聚类分别对应于间距约为4d的顺流向涡对的两个脱落状态。两种间距的顺流向涡均可以被视为A模式,其间距差别源于流动的动力不稳定。值得注意的是,前四种聚类中心与后两种聚类中心需要分别通过两种邻域半径ε1和ε2在决策图中获得,这就表明,获取前四种聚类与后两种聚类的密度评估标准不同,也即意味着聚类结果的判别标准不统一。当MinPts取100和120时,能够利用同一邻域半径ε找到4个明显的聚类中心,分别对应于间距约为5d和4d的顺流向涡对的两个脱落状态。此时相对于MinPts< 100的情况,在保证特征识别准确的同时,聚类数目也更加合理。当MinPts进一步增加,聚类中心缩减为两个,分别对应于顺流向涡脱落的两个状态,但没有能够区分两种涡对展向间距的情况,这也导致聚类中心呈现的涡对出现了不清晰的情况。可见,当MinPts取100~120时,基于Pearson相关距离的OPTICS算法能够通过合适的邻域半径,识别到顺流向涡结构的展向分布间距和旋涡脱落状态。
图11列出了基于夹角余弦相关距离的OPTICS算法获得的决策图和对应的聚类中心。对比图10和图11,会发现基于夹角余弦的流场结构识别结果与基于Pearson相关距离的流场结构识别结果高度相似,参数规律也完全相同。区别仅在于部分聚类的样本数目有微小差距。由表1中两者的定义,可以知道,Pearson相关系数相当于排除均值后样本的夹角余弦,所以采用两种指标计算的核心距离与可达距离应当具备相同的规律,仅在具体数值上有所区别。同时,对于本文选取的涡量场样本,每个样本中除了涡出现的位置存在显著的涡量值,其他大范围的背景涡量值接近于0,这导致各个涡量场样本的均值也接近于0,从而夹角余弦和Pearson相关系数对于涡量场样本的计算结果也差别极小。采用两种指标进行基于OPTICS算法的聚类,其决策图和聚类结果也应当十分接近。
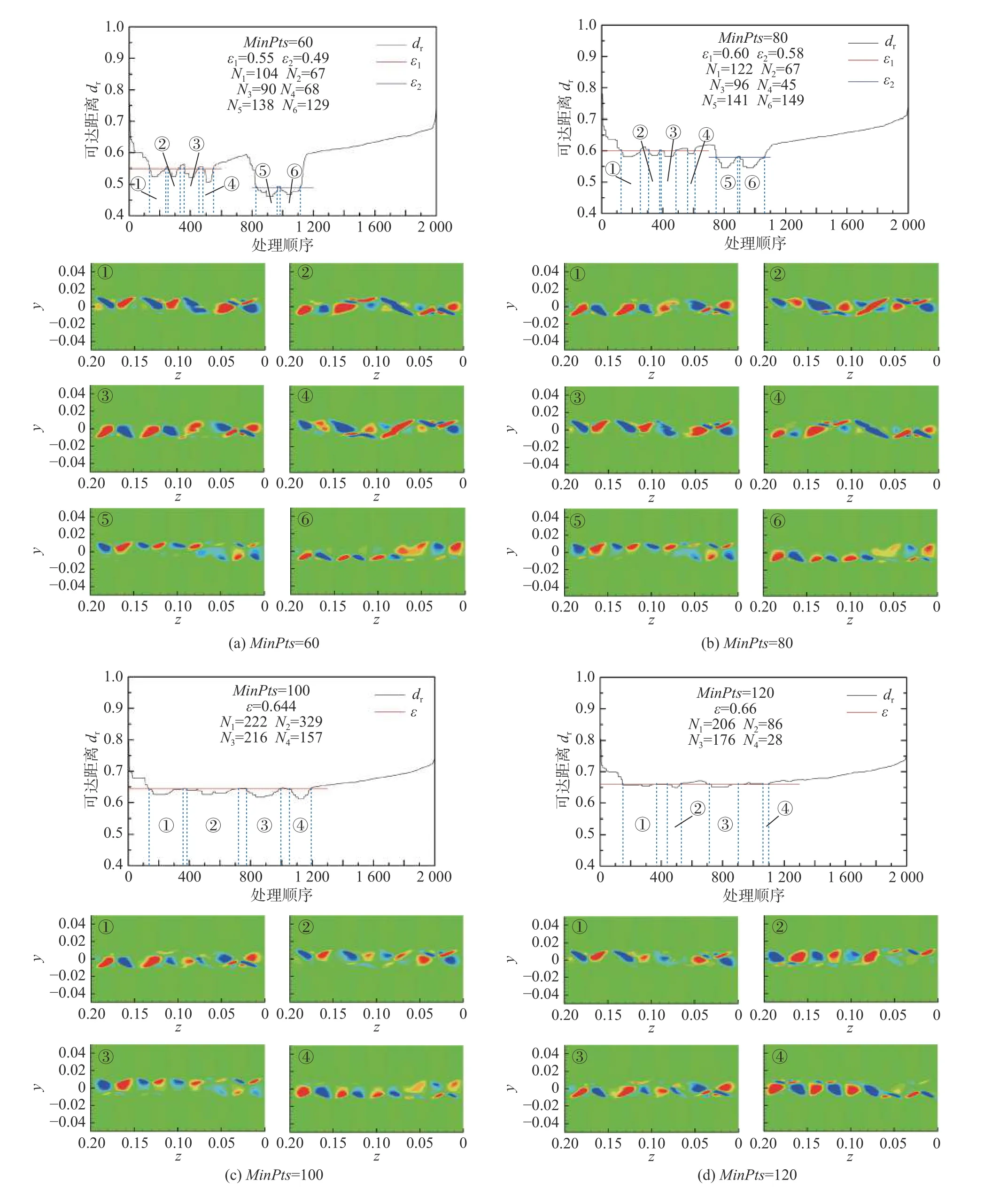

图10 基于Pearson相关距离的OPTICS算法的决策图与聚类中心Fig. 10 The reachability-plots and cluster centers of the OPTICS algorithm based on the Pearson-correlation distance
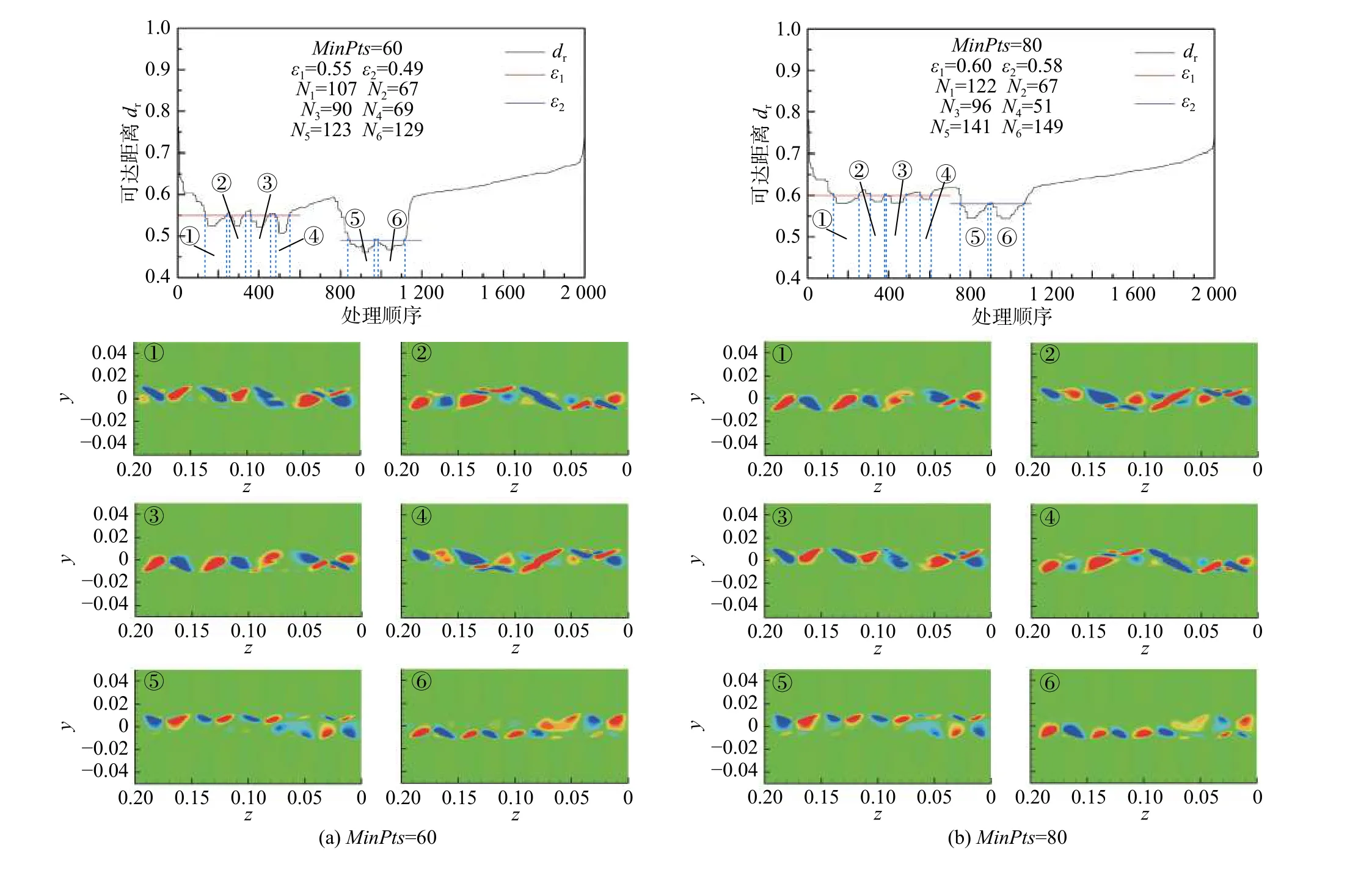
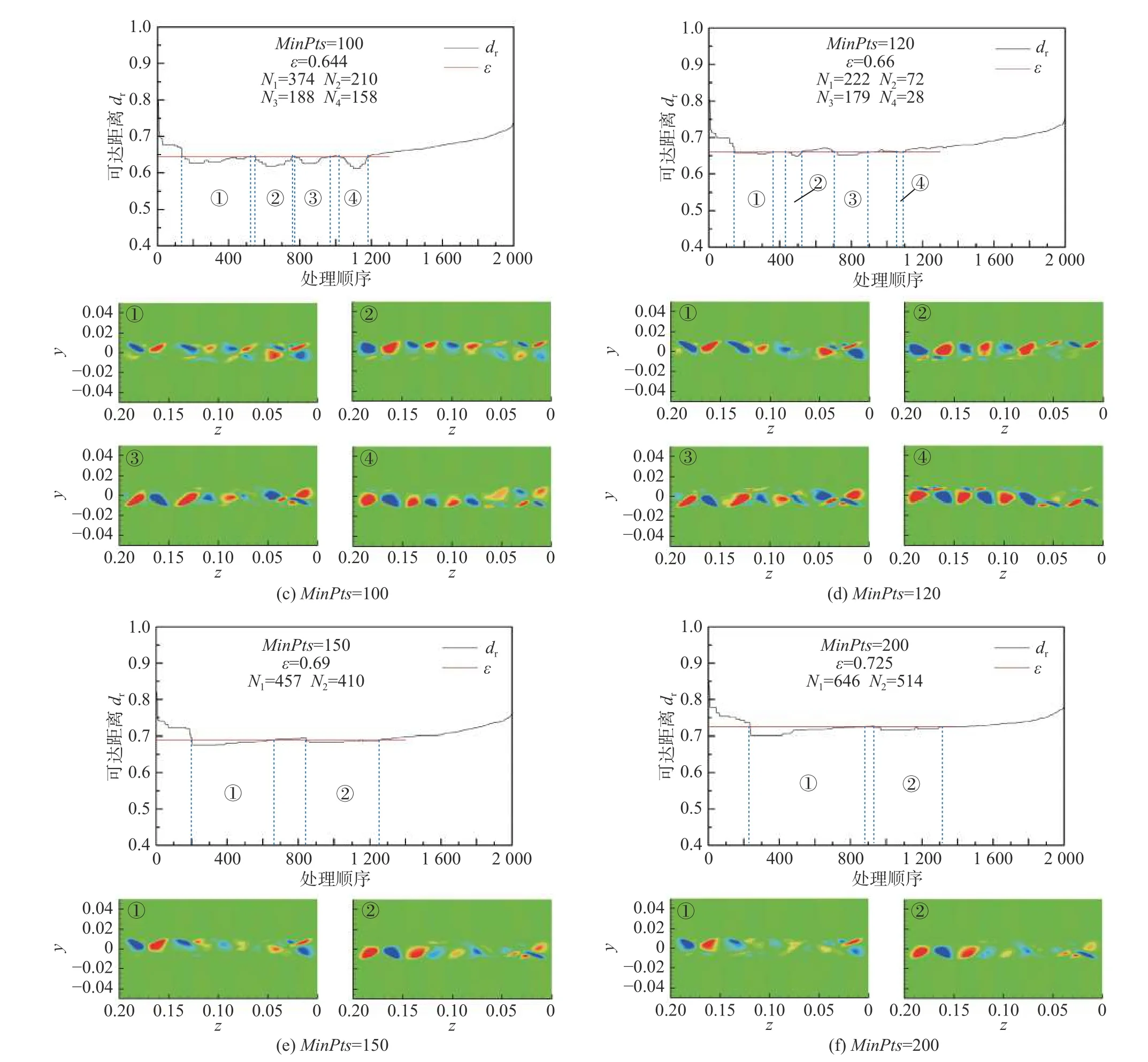
图11 基于夹角余弦相关距离的OPTICS算法的决策图与聚类中心Fig. 11 The reachability-plots and cluster centers of the OPTICS algorithm based on the cosine-correlation distance
图12列出了基于Spearman相关距离的OPTICS算法获得的决策图和对应的聚类中心。Spearman相关系数仅考虑了流场样本中涡量值的排序关系,而忽略了其具体的数值的影响,这对OPTICS算法的聚类结果产生了明显影响。当MinPts取60和80时,能够找到8个明显的聚类中心,但其中仅能清晰识别到间距约为4d的顺流向涡对的脱落状态,而其他的聚类结果并不能清晰地体现涡量场的结构特征。当MinPts= 100时,可以识别出四个聚类中心,分别对应于间距约为5d和4d的顺流向涡对的两个脱落状态;其中间距为5d的顺流向涡的脱落状态不如采用Pearson相关系数或夹角余弦时的结果清晰。而MinPts> 100时,可以找到对应于间距约为5d和4d的两种顺流向涡分布,但无法区分旋涡脱落的状态。这样的结果证明,基于Spearman相关距离的OPTICS算法并不适于流场结构特征的分析。


图12 基于Spearman相关距离的OPTICS算法的决策图与聚类中心Fig. 12 The reachability-plots and cluster centers of the OPTICS algorithm based on the Spearman-correlation distance
表5列出了本节讨论的各种聚类算法用于流场结构特征分析算例的结果对比,结合具体的聚类中心分析结果,基于Pearson相关距离和基于夹角余弦的OPTICS算法在本算例的流场结构分析中获得了准确的分析结果。

表5 不同流场结构特征分析聚类算法的对比Table 5 A comparison of among the different clustering algorithms for analyzing flow structure characteristics
4 基于相关距离的OPTICS聚类算法进行流场结构特征识别的鲁棒性分析
本节考虑基于前述数值模拟获取的流场样本实例,通过在样本中加入噪声的方式,分析样本噪声强度和噪声样本的数量对聚类分析结果鲁棒性的影响。
4.1 测试样本的构造方法与聚类结果的评判指标
前述数值模拟共计获得2000个流场样本,在这些样本中随机抽取一定数量的样本,按下式添加高斯噪声:

式中:xi´表示流场样本X中已添加噪声的样本,xi表示流场样本X中被随机选中的待添加噪声的原始样本,e表示均值为0标准差为1的高斯随机序列,δ则为高斯随机序列的缩放系数,可以表征噪声的强度。测试样本由未被抽取的原始样本和随机抽取后添加噪声的样本混合构造,每种参数工况按3种不同的随机序列分别构造3个测试样本。
考虑到数值模拟获得的涡量场样本,其涡量为101~102量级,所以本节探讨以下7种δ取值:0.1、0.3、1、3、10、30、100,它们对应的噪声样本如图13所示。随机抽取用以添加噪声的样本数目则利用样本代换率Rs表示:
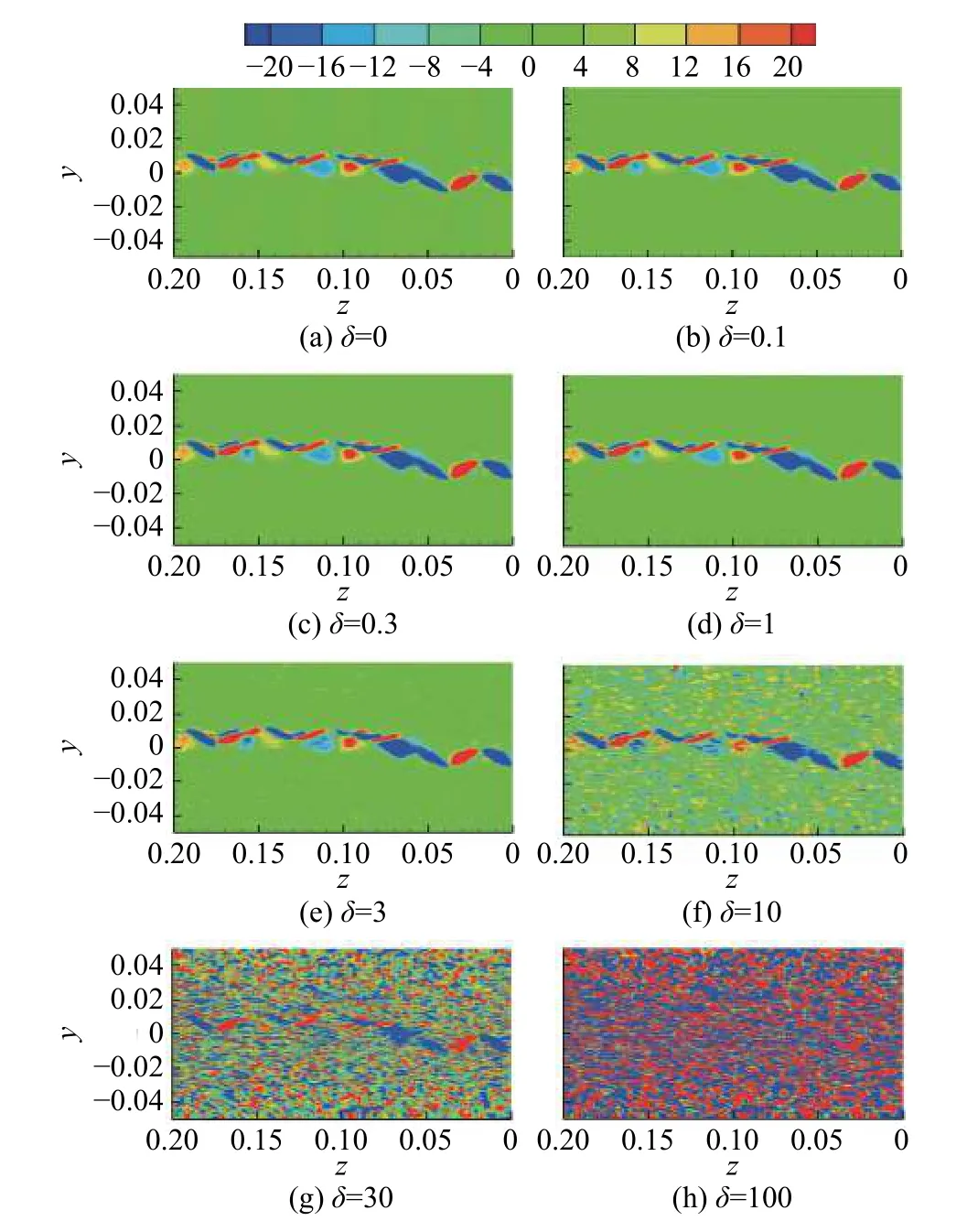
图13 添加不同强度噪声的流场样本示例Fig. 13 The flow fields with different intensities of the Gaussian-noise

本节讨论的Rs取值情况为:1%、2%、5%、15%和50%。
由于流场本身动力系统的复杂性,较难提取到标准的流场结构特征聚类。所以聚类分析结果的评判,要基于测试样本聚类结果相对于原始样本聚类结果的偏移,即衡量测试样本聚类中心和原始样本聚类中心的相关距离。这一衡量指标可以按下式定义为各个聚类中心偏移量的算术平均:

式中:dcenter为基于相关距离的聚类中心偏移指标,N为聚类数目,dc´,c,i表示测试样本C´与原始样本C的第i个聚类中心的相关距离。在原始样本的聚类结果中(图10),MinPts= 100且ε= 0.644的结果可以作为用于衡量聚类结果鲁棒性的基准聚类中心。
4.2 噪声强度δ对聚类结果的影响规律
图14列出了各种样本代换率下,dcenter随噪声强度δ的变化规律。可见针对所有的Rs设置,dcenter均随δ的增长而增加;在对数坐标下,dcenter的增长随着δ的增长而趋缓。这表明,当噪声强度较大时,噪声强度对聚类中心的偏移影响减小。当样本代换率Rs≤5%,噪声强度造成的聚类中心偏移的相关距离普遍不超过0.05,也即意味着此时测试样本的聚类中心与原始样本的聚类中心高度相关,聚类结果稳定。此时,流场样本的噪声对流场结构识别结果几乎没有影响。当样本代换率Rs≥15%,在引入较小噪声(δ≤10)时,测试样本的聚类中心偏移量最大约为0.10,此时测试样本的聚类中心与原始样本的聚类中心仍然高度相关。但当引入较大噪声(δ≥30)时,部分测试样本已经无法被识别到对应于原始样本聚类中心的四种聚类,因此在图14(d)和图14(e)中缺失了部分样本δ≥30的数据点,此时基于相关距离的OPTICS聚类算法无法在原有的初始参数设置下实现流场结构特征分析识别。
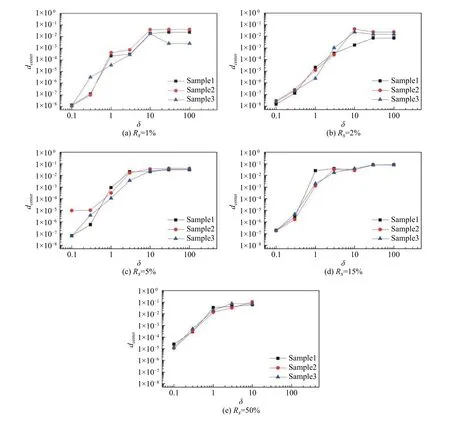
图14 噪声强度δ对聚类中心偏移量dcenter的影响Fig. 14 Effects of the noise intensity (δ) on the displacements of the clustering centers (dcenter)
4.3 样本代换率Rs对聚类结果的影响规律
图15列出了噪声强度0.1≤δ≤10时,dcenter随样本代换率Rs的变化规律。针对所有的δ设置,dcenter均随Rs的增长而呈现大致增长的趋势;在对数坐标下,dcenter的增长率随着δ的增加而下降。这表明,当噪声强度增加时,样本代换率对聚类中心的偏移影响减小。根据图15,当噪声强度有限时,样本代换率几乎不影响基于相关距离的OPTICS算法的流场结构特征识别的结果。
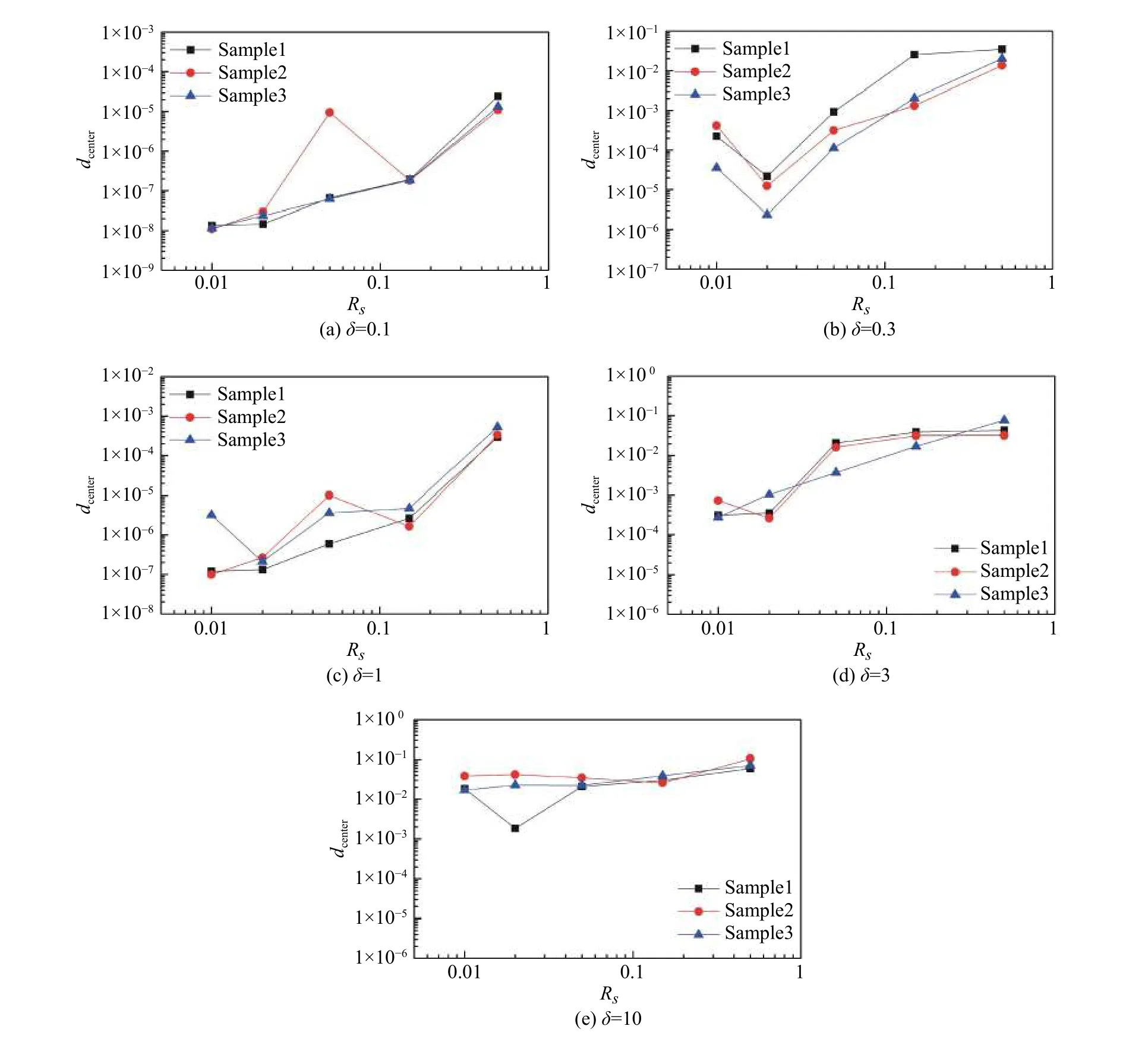
图15 样本代换率Rs对聚类中心偏移量dcenter的影响Fig. 15 Effects of the sample-replacement ratio (Rs) on the displacements of the clustering centers (dcenter)
5 结论
本文基于OPTICS聚类算法,在分析流场数据特征与多种相似度评判指标的基础上,引入相关距离的概念加以改进,提出利用基于相关距离的OPTICS算法进行流场结构特征分析。该方法依托基于Pearson相关系数的相关距离指标,不需要动力学假设,仅依靠数据驱动。本文通过基于LES的CFD数值模拟,对经典的圆柱绕流问题进行瞬态计算,获取了2000个流场样本。以识别顺流向涡的旋涡脱落状态和A模式分布为目标,对比了k-means、原始的OPTICS、基于闵可夫斯基距离的OPTICS和基于相关距离的OPTICS等聚类算法的有效性,并对基于Pearson相关距离的OPTICS识别流场结构特征的鲁棒性进行了分析。结果表明:
1)相对于k-means算法、原始的OPTICS算法和基于闵可夫斯基距离的OPTICS算法,基于Pearson相关距离的OPTICS算法可以有效识别出圆柱尾流中顺流向涡脱落的两种状态,以及A模式顺流向涡的两种不同的展向间距。针对本文的算例,基于夹角余弦相关距离的OPTICS算法也可以获得与基于Pearson相关距离的OPTICS算法高度相似的结果,其原因在于算例样本的元素均值几乎为0,样本元素均值对于夹角余弦的影响很小;而基于Spearman相关距离的OPTICS算法的识别结果相对不够清晰,适宜的初始参数范围较小。
2)基于Pearson相关距离的OPTICS算法,可以在MinPts取100~120时,通过设置合适的邻域半径,识别到顺流向涡结构的展向分布间距和旋涡脱落状态。MinPts取值小于100会导致流场结构聚类结果的过度分类,而MinPts取值大于120时会失去识别顺流向涡展向间距的能力。
3)相对于k-means算法,基于各种相似度指标的OPTICS算法均提升了聚类结果的稳定性,降低了聚类结果对初始参数的敏感性,保证了在确定的初始参数下,聚类结果唯一。相关距离概念的引入则改善了原始OPTICS算法对流场结构特征的识别能力,其中以Pearson相关系数和夹角余弦为指标计算的相关距离效果最佳。
4)基于Pearson相关距离的OPTICS算法,当初始参数设置为MinPts= 100时,在噪声样本量少于总样本量的5%时,可以在高强度高斯噪声(δ≤100)样本的干扰下,依然识别到清晰的流场结构特征,噪声样本造成的聚类中心偏移的相关距离不超过0.05;而当噪声样本量超过样本总量15%时,基于相关距离的OPTICS算法可以在引入δ≤10的噪声强度下实现较稳定的流场结构特征识别,噪声造成的聚类中心偏移的相关距离不超过0.10。
