分布式连接全装配RC 楼盖人行荷载试验与振动舒适度分析

2021-11-12王文康许清风张天鹏

工程力学 2021年10期

王文康，庞瑞，许清风，周飞，张天鹏

(1. 河南工业大学土木工程学院，郑州 450001；2. 上海市建筑科学研究院有限公司，上海市工程结构安全重点实验室，上海 200032)

随着楼盖结构向“跨度大、自重轻、体系柔、阻尼低”的方向发展，楼盖在人行荷载下的振动问题越来越明显，常引起人的不适[1-4]，甚至引起共振而导致结构的破坏[5-6]，楼盖的振动问题受到国内外学者的广泛关注[7-10]。我国标准对楼盖舒适度的要求通常是采用控制自振频率下限和峰值加速度上限的双重标准，如规范[11]中规定各类大跨度楼盖的自振频率不得小于3 Hz，楼盖的峰值加速度不得大于0.15 m/s2。

近年来，随着装配式建筑的快速发展，装配式楼盖在国内外得到了广泛应用[12]。预制混凝土楼盖体系可分为“干式”和“湿式”两种[13]：“干式”体系为通过连接件连接预制板的全装配楼盖体系；“湿式”体系包含混凝土后浇层与连接件同时采用的“组合楼盖”和仅有后浇层的“非组合楼盖”两种形式。目前，我国装配式建筑主要采用“等同现浇”的设计与建造方式，常在预制底板上加后浇层形成叠合式楼盖[14]。叠合式楼盖的自重较大，同时也不利于高强与高性能材料、预应力等高技术的充分利用。因此，全装配RC 楼盖在北美和欧洲等国家应用较为普遍，我国《装配式多层混凝土结构技术规程》(T/CECS 604-2019)[15]也对全装配楼盖的应用做出了相关规定。

干式连接双T 板楼盖是应用较多的全装配式楼盖，可满足大跨、重载等现代楼盖的设计要求，但结构高度较大、板底面不平整，应用范围有局限。基于此，课题组研发了一种分布式连接全装配RC 楼盖 (Discretely connected precast RC diaphragm,DCPCD)，如图1 所示。

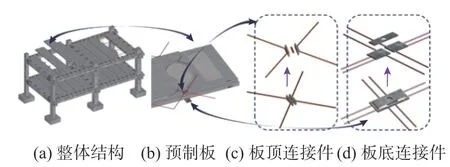
图1 DCPCD 示意图Fig. 1 Diagram of DCPCD

DCPCD 是由若干个预制企口板在梁上吊装平铺组成的全装配式楼盖体系，拼接板缝处的“L”型企口上下咬合，梁(墙)-板之间和板-板之间均通过预埋成对的钢连接件焊接连接，从而实现了全干式连接。

国内外学者对装配式楼盖的竖向振动问题已开展了广泛研究。Liu 等[16]进行了3 种不同材料特性(正交各向异性材料，带状的各向同性材料和各向同性材料)的壳模型对该空心楼盖进行深入分析，确定了每个壳模型中最佳材料参数，并指出正交各向异性材料的壳是最佳模型选择；刘界鹏等[17]对预制带直肋底板混凝土叠合板进行单人行走(落足)荷载下的振动舒适度研究，提出了加速度峰值反应系数和均方根加速度峰值反应系数的建议值；Wen 等[18]对一种新型的预制空心跨网格地板系统的振动舒适度进行了试验研究，并提出了有限元的分析方法，分析结果表明该类楼盖具有良好的振动舒适度特性。

DCPCD 垂直于板缝方向(以下简称横板向)采用分布式连接件连接，特殊的构造形式导致其竖向承载力和振动特性与现浇楼盖相比有所差异。已有的研究[19-21]表明：DCPCD 具有良好的平面内刚度、竖向承载力以及竖向振动性能，庞瑞等[22]又进行了对边简支的单向板在单人踮脚、跳跃荷载激励下的动力试验，研究了板缝和连接件对DCPCD 振动特性的影响。为进一步揭示DCPCD在人致激励下的动力响应，进行了DCPCD 试件和现浇楼盖对比试件在四边简支条件下的动力特性试验和人行荷载试验，以期为DCPCD 舒适度设计与性能评价提供依据。

1 试验概况

1.1 试件设计

试验试件包括2 个DCPCD 试件和1 个现浇楼盖(Cast-in-situ slab, CISS)试件，试件尺寸均为3700 mm×3700 mm。DCPCD 试件由若干块预制板通过发卡-盖板混合式(Hairpin connectors & coverplate connectors, HPC-CPC)板缝连接件连接，各试件设计参数见表1。试件平面布置如图2 所示(以试件S5C5 为例)。

表1 试件设计参数Table 1 Design parameters of the specimens

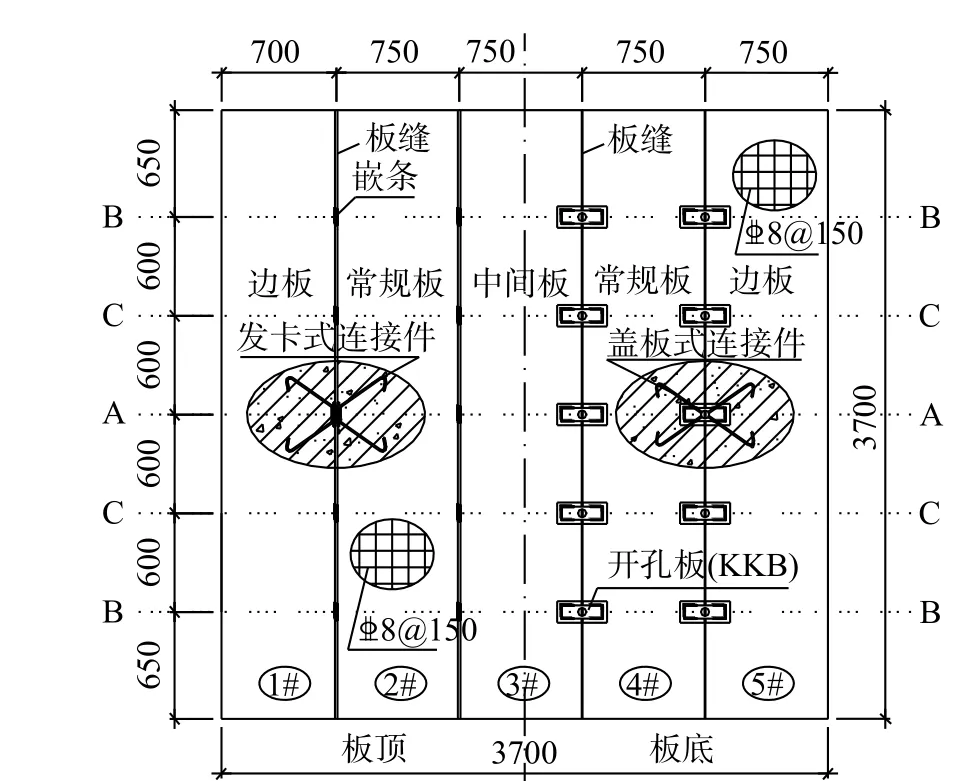
图2 试件S5C5 平面布置图 /mmFig. 2 Plane view of specimen S5C5

HPC 通过嵌条焊接为一体，CPC 通过开孔板焊接为一体，连接件详图和实体图详见图3 和图4。

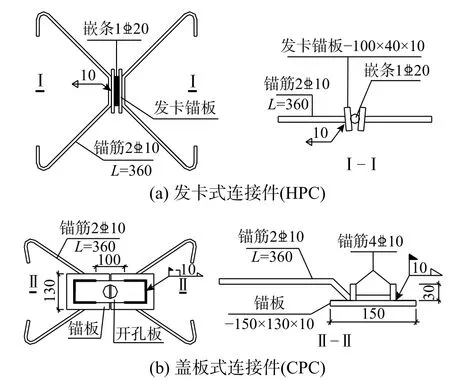
图3 连接件详图 /mmFig. 3 Connection details

图4 板缝连接件实体图Fig. 4 Photos of slab joint connectors

1.2 材料性能

试件内的钢筋均为HRB400 级钢筋，钢板均为Q345 级钢，厚度为10 mm，实测3 组式样抗拉试验的平均参数见表2。混凝土等级为C35，与试验试件同条件养护的标准试块的实测参数见表3。

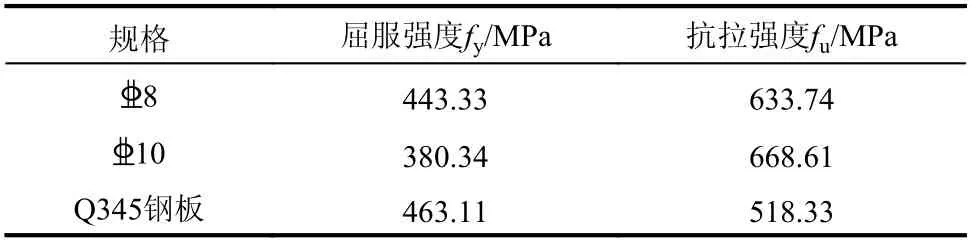
表2 钢筋(板)实测力学性能Table 2 Mechanical properties of steel bars (plates)

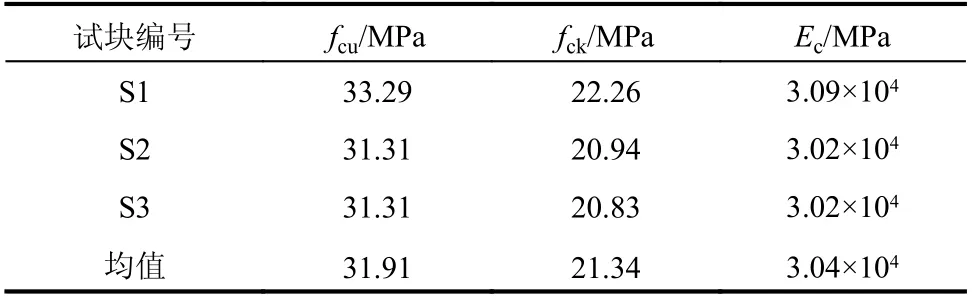
表3 混凝土实测力学性能Table 3 Mechanical properties of concrete

1.3 试验装置

加载前，先将试件平放于支承钢框架上，以模拟四边简支的支承条件，试验装置图详见图5。

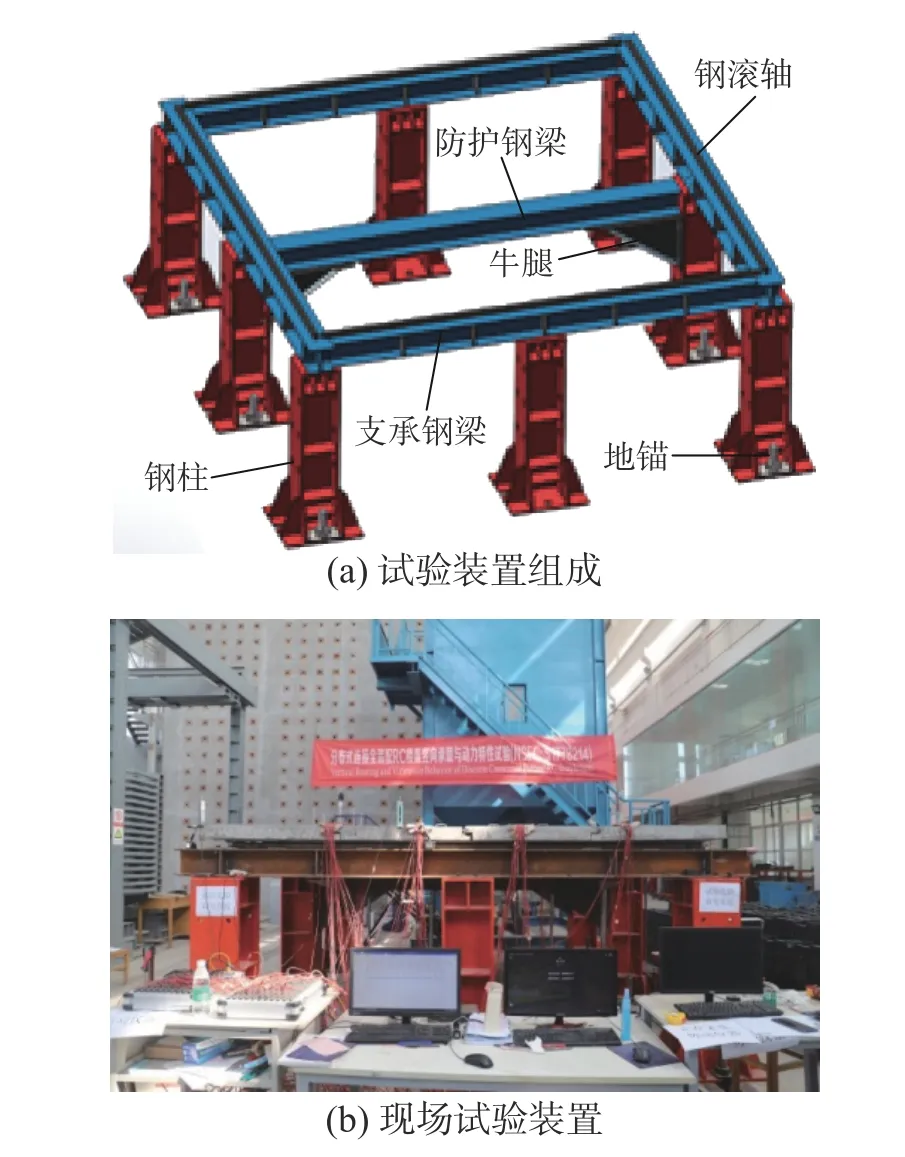
图5 试验装置Fig. 5 Test setup

2 基于锤击法的模态参数分析

楼盖的模态参数主要包括模态振型、自振频率和阻尼比[23-24]，通过对楼盖模态参数的研究可了解其基本动力特性，提前预测楼盖的振动反应是否符合规范要求，分析DCPCD 与现浇楼盖之间动力特性的异同，为结构的优化设计提供依据。

试验中对于DCPCD 模态参数的分析是基于锤击法的冲击试验。试验设备主要有脉冲锤、加速度传感器和动态采集仪DH-5922D。脉冲锤的量程为2 kN，采用ICP 压电型加速度传感器，动态采集仪的采样频率设定为500 Hz，激励方式为单点激励，流程图如图6 所示。

图6 锤击试验流程图Fig. 6 Flow chart of hammer test

加速度传感器的布置原则为：① 各特征点处；② 加速度可能较大处；③ 尽量避开振型节点；④ 布置足够丰富的测点。各测点布置见图7。

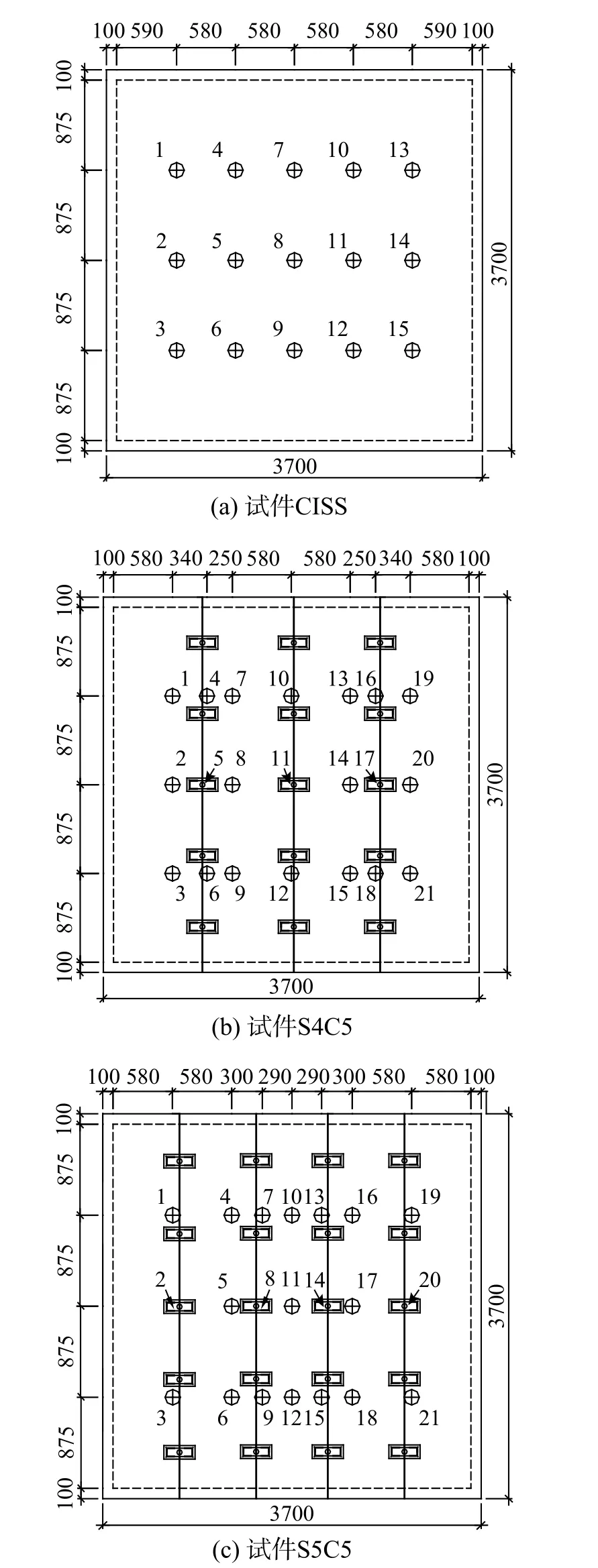
图7 加速度传感器布置图 /mmFig. 7 Layout of acceleration sensors

2.1 试验结果分析

动力特性试验中，取5 次激励响应的平均值作为代表值以避免偶然误差，从而提高测试可靠性，通过对频响函数的参数识别可进行模态分析。图8 所示为现浇楼盖中测点4 处的响应信号。

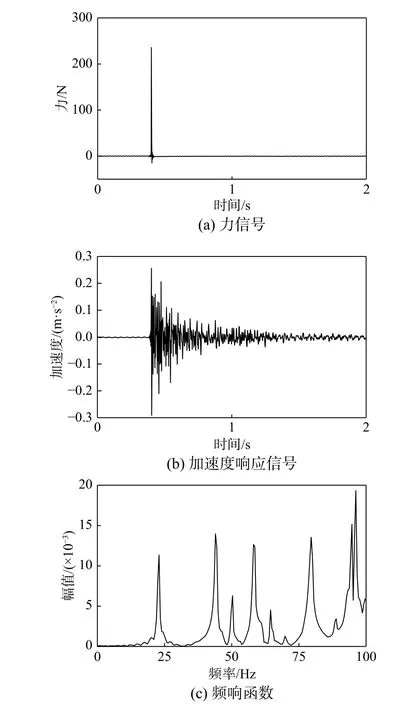
图8 CISS 试件测点4 锤击响应信号Fig. 8 Four-point hammer response signal of CISS specimen

为了研究连接件的位置对DCPCD 自振频率的影响，按照未焊连接件、焊A 排连接件、焊B 排连接件、焊C 排连接件的顺序分别进行锤击试验(连接件排列编号详见图2)。实测各焊接情况下DCPCD 试件的一阶自振频率(基频)如图9 所示。

由图9 可知：DCPCD 的基频与连接件的数量呈正比，焊接A 排连接件后频率变化的最多，平均增加了8.05%，而焊接C 排连接件后频率变化的最少，平均增加了2.36%，说明靠近跨中和边缘的连接件对楼盖的自振频率影响较大。全焊后DCPCD 的基频平均增加了15.05%，说明连接件可有效提高DCPCD 的基频，改善其振动性能。

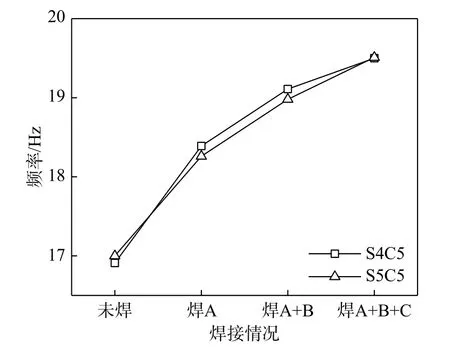
图9 各工况下一阶自振频率Fig. 9 First-order natural frequency of each working condition

通过参数识别方法对锤击法得到的频响函数进行分析可得到模态振型，各试件实测前三阶振型如表4 所示。由表4 可知：DCPCD 与现浇试件的第一阶模态相同，第二阶、第三阶模态均不相同，这反映了现浇楼盖双向同性、DCPCD 双向异性的差异，因为拼接降低了DCPCD 横板向的抗弯刚度，因此，第二阶模态为沿该方向的弯曲形式。

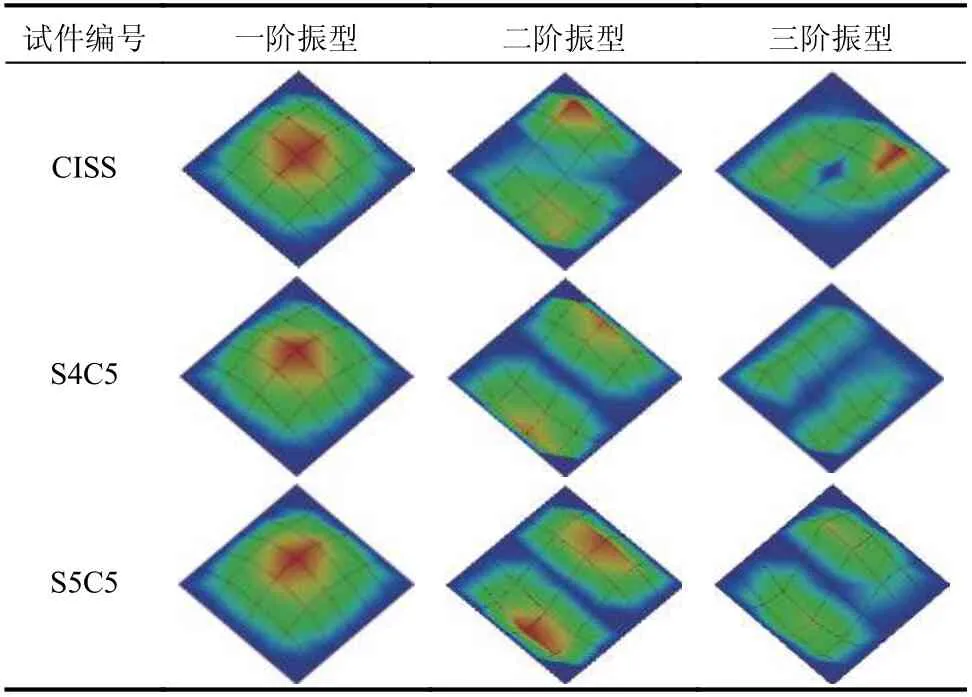
表4 前三阶振型Table 4 First three order mode shapes

3 人行荷载试验

人行荷载试验包括单人激励和多人(4 人与8 人)激励，各工况的步频见表5。在行走路线上(见图10)标出落足点来控制步幅和频率，观测DCPCD 在各工况下的振动响应。

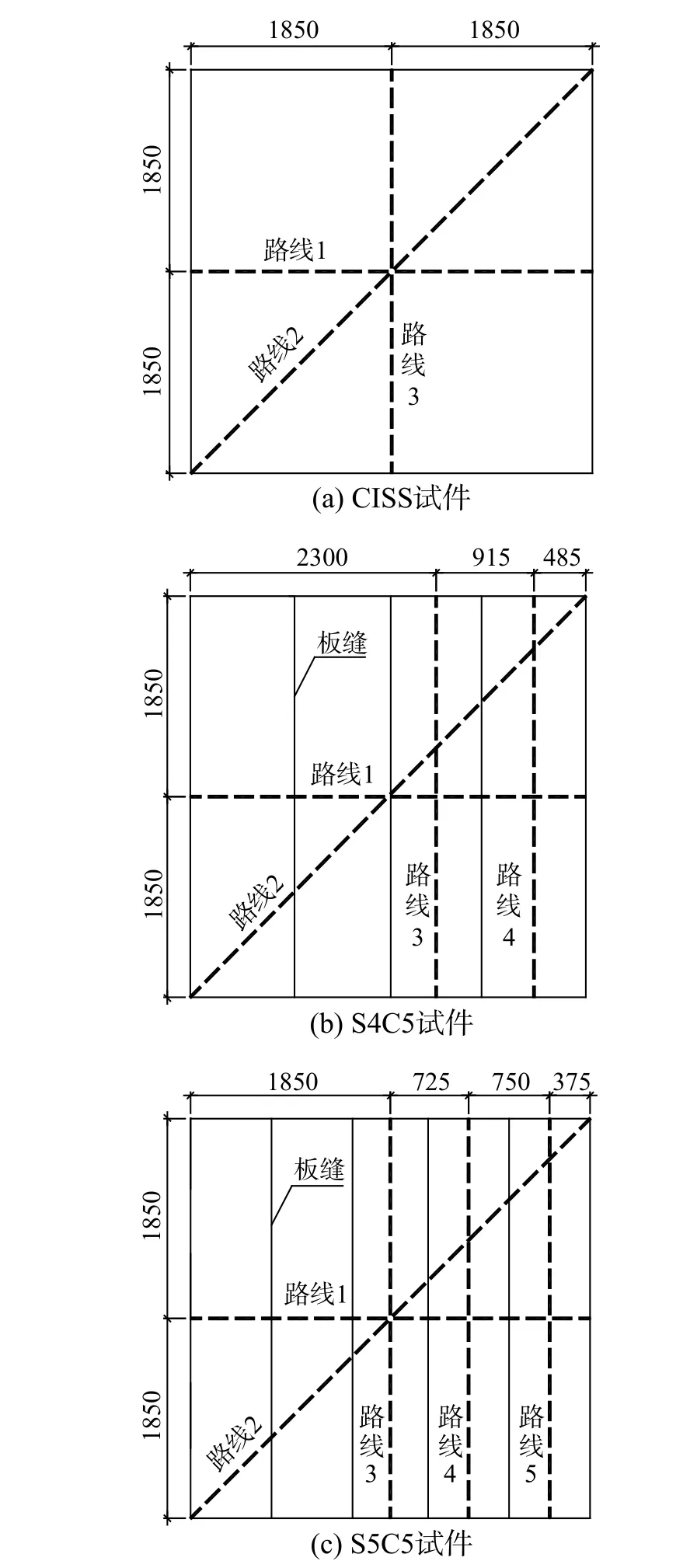
图10 行走路线示意图 /mmFig. 10 Schematic diagram of walking route

表5 行走激励相关参数Table 5 Parameters of walking excitation

按照AISC 规范[25]，人体的重量服从均值为700 N，标准差为145 N 的正态分布，试验场景见图11。

图11 人致激励现场照片Fig. 11 Photos of human incentive test

3.1 各排连接件对楼盖振动响应的影响

DCPCD 试件实测加速度随连接件焊接情况的变化规律详见图12。由图12 可知：峰值加速度随连接件焊接数量的增加而明显降低；焊接A 排连接件后加速度降低最显著，单人激励下平均降低37.92%，8 人激励下平均降低29.54%；全焊后单人激励下加速度平均降低71.91%，8 人激励下平均降低63.105%。说明布置一定数量的连接件可有效降低峰值加速，改善楼盖的舒适度。

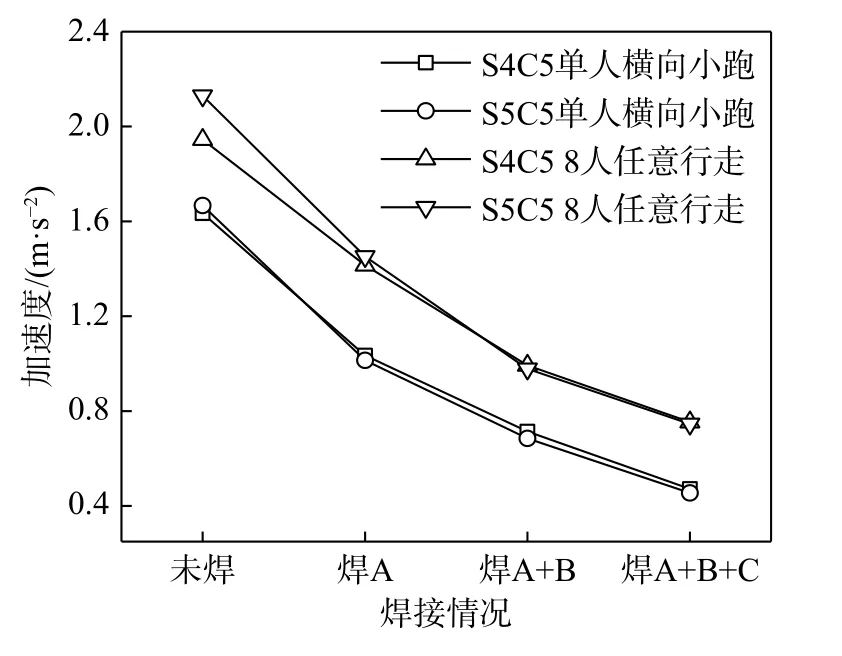
图12 各工况下的峰值加速度Fig. 12 Peak acceleration of each working condition

3.2 不同激励方式下的模态参数

楼盖的振动加速度响应与荷载作用下的能量密切相关[2]，图13 为人行荷载下各试件中不同测点的功率谱密度(Power spectral density, PSD)，各峰值点对应的各特征频率即为楼盖的各阶自振频率，表明楼盖振动时的能量主要集中在自振频率附近。由图13 可知：

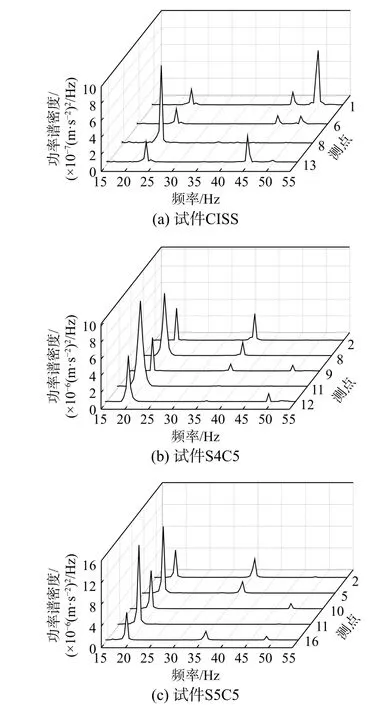
图13 功率谱密度分布Fig. 13 Power spectral density distribution

1)同一试件中各个测点的功率谱密度峰值出现的位置相近，表明通过不同的测点测得楼盖的自振频率相近，楼盖的自振频率和频域分布与测点的位置无关。

2)楼盖的能量分布主要集中在低阶模态，但不同测点的功率谱密度的峰值位置存在差异，处于某阶振型中心测点的功率谱密度峰值出现在该阶振型频率附近，如现浇试件中测点1 位于第三阶振型中心附近，所以该测点的功率谱密度分布主要集中在第三阶振型频率附近。

3)位于某一阶振型节点附近的测点在该阶频率附近的功率谱密度接近于零，即丢失该阶模态信息。如试件S4C5 中的测点2、测点8 和测点11均位于第三阶振型的节点上，故在第三阶振型频率附近的功率谱密度接近于零；测点11 和测点12位于第二阶振型的节点上，故在第二阶振型频率附近的功率谱密度接近于零。因此，为避免模态参数信息的缺失，应该取足够丰富的测点数据作为分析对象。

4)对于同一阶振型，越靠近振型中心测点的能量分布越大，振动响应越大；越远离振型中心测点的能量分布越小，振动响应越小。

图14 幅频曲线Fig. 14 Amplitude-frequency curve

通过力锤激励与人致激励两种方法得到的楼盖前三阶自振频率和阻尼比见表6，由表6 可知：

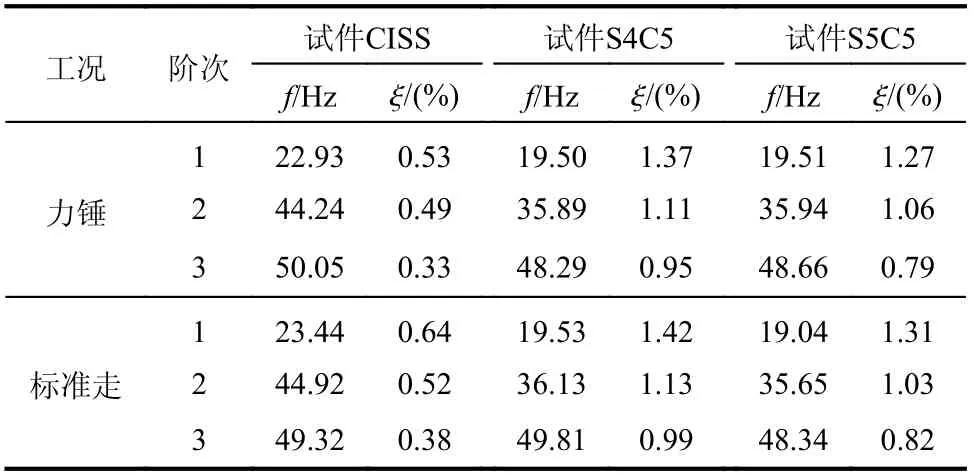
表6 楼盖在不同荷载下的自振频率和阻尼比Table 6 Natural frequencies and damping ratios of floors under different loads

1)楼盖的前三阶自振频率和阻尼比在力锤和标准走两种激励作用下的测试结果相近，表明自振频率和阻尼比是结构本身固有的动力特性，只与结构的质量、刚度、材料、连接方式和结构形式有关，与外部激励类型无关。

2) DCPCD 试件自振频率小于现浇试件，一阶频率平均降低15.83%；试件S5C5 的自振频率略大于试件S4C5，与文献[19]的结论不符(楼盖横板向刚度与板缝数成反比)，其原因为试件S4C5有一条板缝位于跨中，对楼盖整体刚度削弱较大。

3) DCPCD 试件的阻尼比大于现浇试件，试件S4C5 和试件S5C5 的一阶阻尼比平均分别为试件CISS 的2.38 倍和2.21 倍，且阻尼比均随模态阶数增加而减小。DCPCD 试件的各阶阻尼比都较现浇试件大，表明板缝可增大结构阻尼。

3.3 加速度响应时程曲线

为研究楼盖的振动传递规律，对现浇试件和DCPCD 试件不同测点在单人横板向慢走下的加速度响应及均方根(RMS)值进行了对比分析，分析结果如图15 所示，由图15 可知：峰值加速度通常出现在时程曲线的中间时段，此时人刚好行至楼盖的中心区域，表明楼盖中心为振动敏感位置。越靠近低阶振型中心处测点的加速度越大，越靠近支座处越小。DCPCD 试件与现浇试件振动传递规律相同，同一工况下，不同预制板上不同测点的加速度及RMS 值变化走势相同，不会产生不一致波形，说明连接件可有效传递楼盖中的横板向振动。

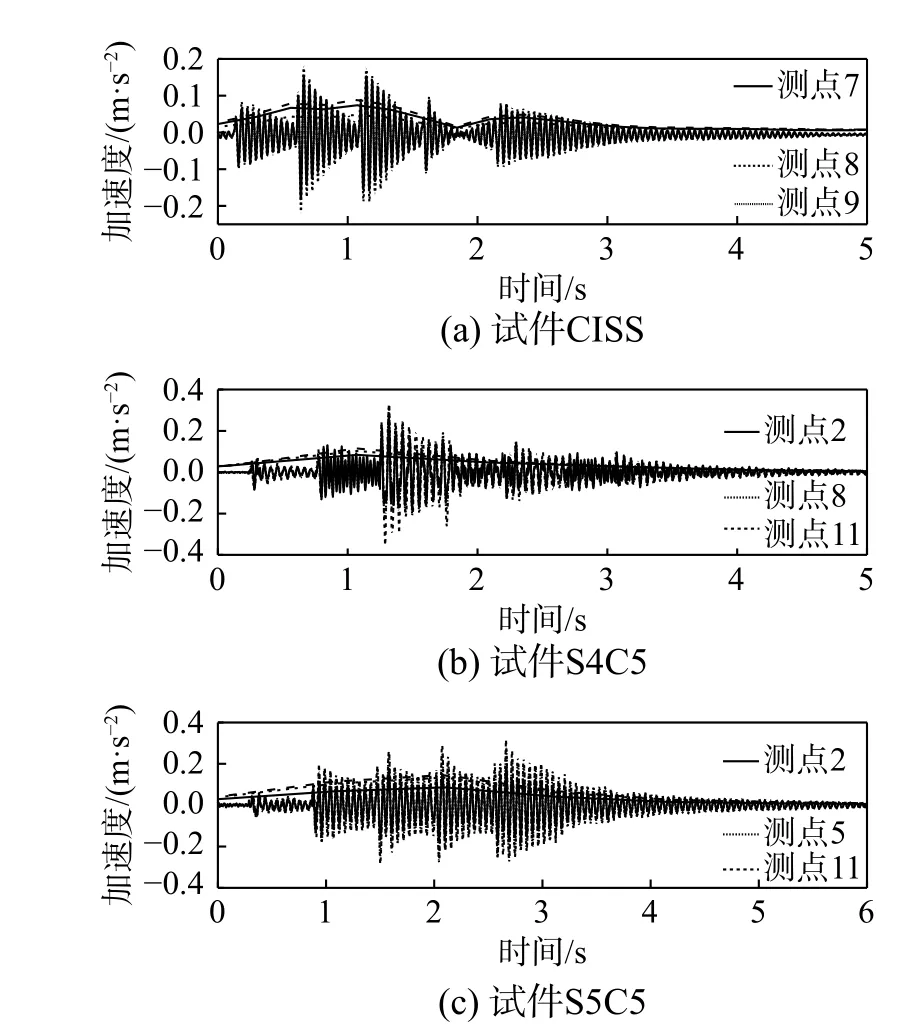
图15 各试件的加速度响应与RMS 值(粗线)Fig. 15 Acceleration response and RMS values(bold lines) of each specimen

3.4 不同步频下的振动响应

人行走时步频随时发生变化，为研究行走步频对DCPCD 振动响应的影响，采用单人沿路线一以不同步频的行走工况进行试验，实测各试件的峰值加速度见图16。由图16 可知：1) DCPCD 试件的加速度响应更大，说明其对振动更加敏感；2)楼盖的峰值加速度与激励频率成正比；3)当板缝位于跨中时楼盖的峰值加速度更大，设计时应将板缝远离跨中，以降低不满足舒适度要求的概率。

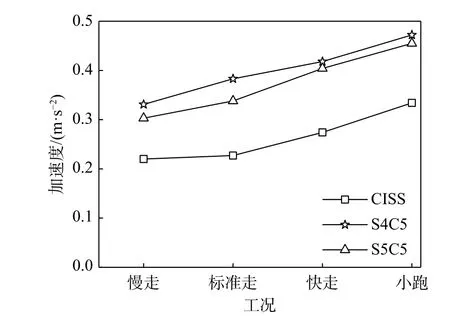
图16 各工况下的加速度响应Fig. 16 Acceleration response under various conditions

3.5 不同行走路线下的振动响应

为研究不同行走路线对DCPCD 振动响应的影响，确定最不利行走路线，采用单人沿不同路线以不同步频的行走工况进行试验，各行走路线下楼盖的峰值加速度见图17。

由图17 可知：1)对于试件CISS，沿对角线方向为最不利行走路线，此路线经过一阶振型和二阶振型的中心，峰值加速度最大；2)对于DCPCD试件，沿横板缝方向为最不利行走路线，峰值加速度最大，沿对角线方向行走时峰值加速度次之，沿顺板缝方向行走时峰值加速度最小，说明板缝的存在降低了横板向的弯曲刚度，使第二阶振型为沿横板向反向对称。

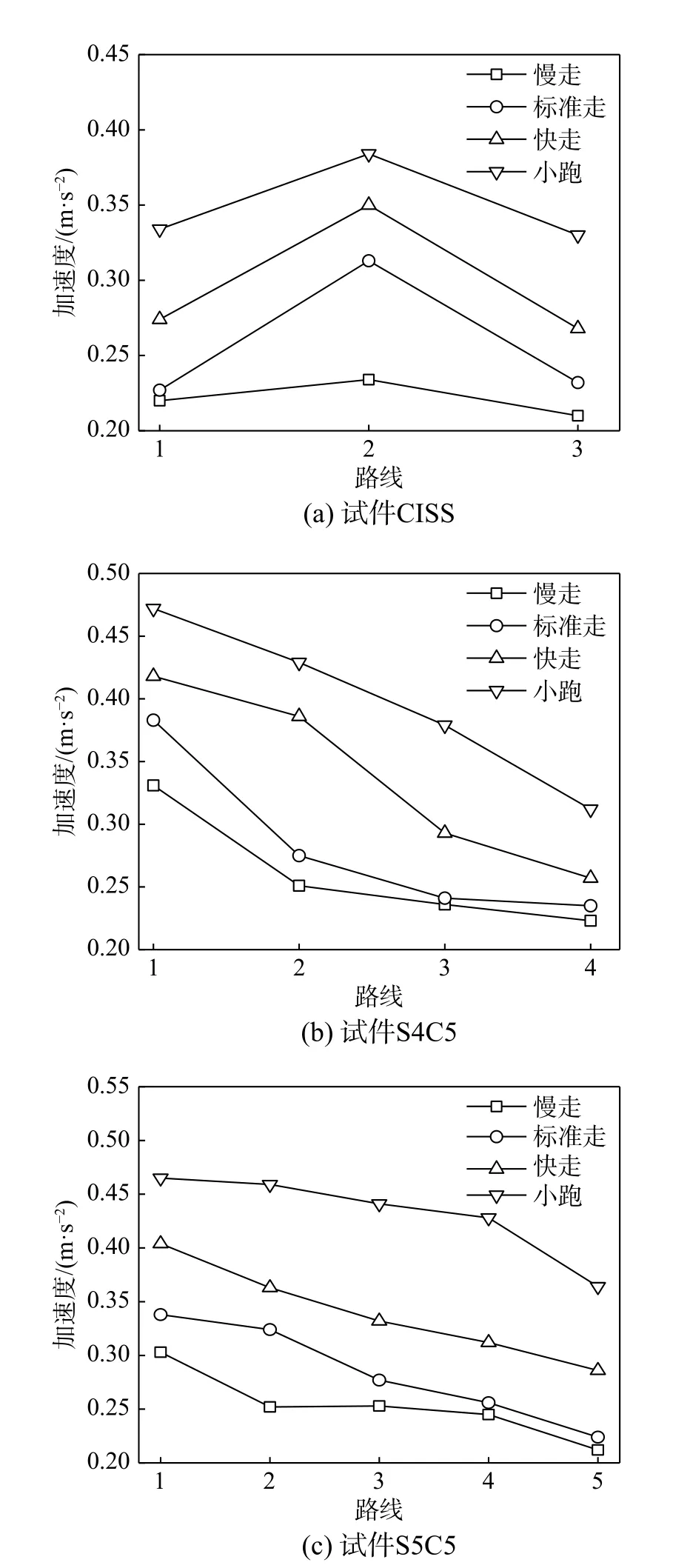
图17 不同行走路线下楼盖的峰值加速度Fig. 17 Peak acceleration of floor under different walking paths

3.6 不同荷载分布形式下的振动响应

多人行走可分为分散行走和聚集行走，不同区域有不同的荷载分布密集度。为研究荷载分布形式对DCPCD 振动响应的影响，采用4 人分散并排行走和4 人聚集两排行走(见图18)的工况进行试验，各试件的加速度响应如表7 所示。

图18 现场照片Fig. 18 Live photos

表7 4 人并排和两排行走下的峰值加速度Table 7 Peak acceleration when four people walking in one row and two rows

由表7 可知：楼盖在4 人聚集两排行走时的峰值加速度均大于4 人分散一排行走时的峰值加速度，即相同荷载大小下，荷载分布的密集度越大，在结构上的作用越明显，振动响应越强烈。

3.7 多人群荷载及不同布载组合下的振动响应

为研究多人群荷载对DCPCD 振动响应的影响，采用稍密状态的人数设定(0.3 人/m2～0.6 人/m2)，8 人在特定位置进行人行激励试验的人群密度为0.58 人/m2。主要有8 人任意行走和不同布载方式下任意行走两类工况。将DCPCD 试件不同位置的预制板进行分类(见图2)，对人群进行不同方式的布载组合，以观测最不利布载方式。

各试件在8 人任意行走工况下的加速度响应时程曲线如图19 所示。

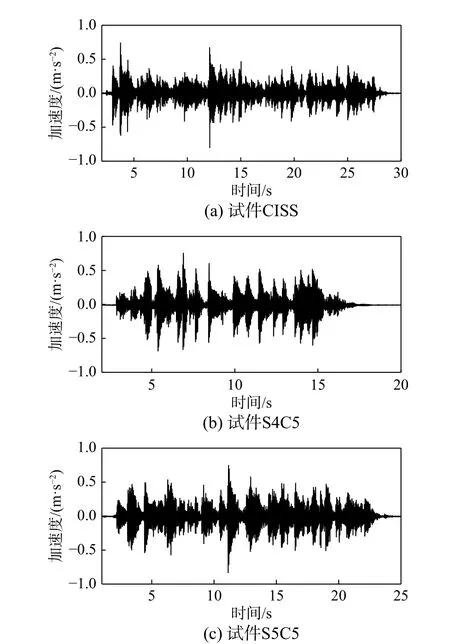
图19 8 人任意行走荷载下的加速度响应Fig. 19 Acceleration response under eight-people random walking load

由图19 可知：多人激励时DCPCD 的加速度仍然比现浇楼盖大，与单人激励结果相一致，但是加速度响应时程曲线较为平稳，因为人群行走具有非协调性[26]。

多人群荷载的布载工况如下：工况1 为8 人任意行走；工况2 为两个常规板(中轴线上五等分点处，后同)各4 人任意行走；工况3 为一个常规板、一个边板各4 人任意行走；工况4 为一个中间板、一个常规板各4 人任意行走。实测人群荷载下的峰值加速度如表8 所示，由表8 可知：

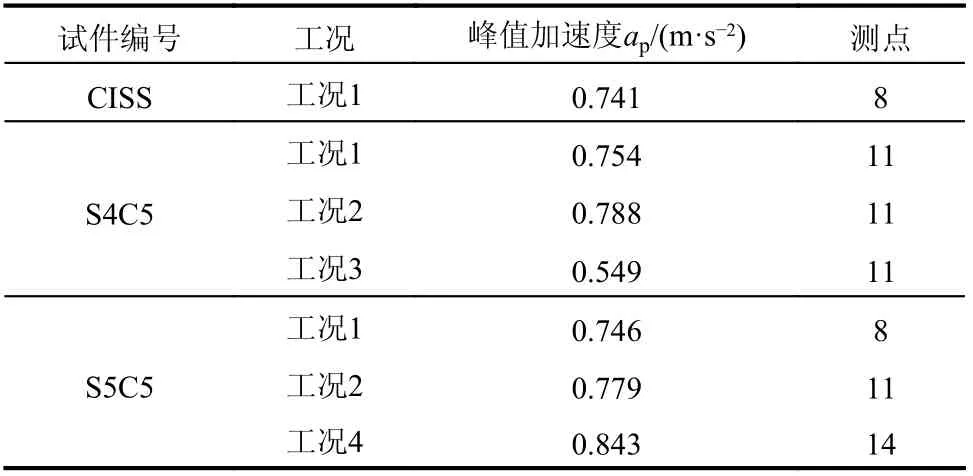
表8 人群荷载下的峰值加速度Table 8 Peak acceleration under crowd load

1)在同样的8 人任意行走工况下，峰值加速度规律为试件S4C5 最大，试件S5C5 次之，试件CISS 最小，与单人激励时的规律一致，即峰值加速度随着自振频率的降低而增大。

2)现浇试件的峰值加速度出现在楼盖中心，为一阶振型的中心；试件S4C5 的峰值加速度出现在跨中板缝的中心，这里既是一阶振型的中心，也是楼盖抗弯刚度较小处；试件S5C5 的峰值加速度通常出现在楼盖的中心，但当荷载位置分布不均匀时峰值加速度也出现在靠近跨中板缝的中心，因为板缝处约束较薄弱，对振动更敏感。

3)对于试件S4C5，工况2 时加速度最大，对于试件S5C5，工况4 时加速度最大，即荷载越靠近楼盖的一阶振型中心则加速度越大，越接近支座处则加速度越小。

4 理论计算

楼盖自振频率和加速度的理论计算可提前预测动力特性和竖向振动加速度响应，判断楼盖是否满足规范中舒适度相关指标要求，从而为楼盖的振动分析与设计提供依据。

4.1 自振频率的理论计算

对于现浇试件，可按照双向同性四边简支矩形薄板的自振频率公式进行计算：

DCPCD 应按照正交双向异性板计算，具体计算过程参考文献[27]，其主要思路为：

1)参照圣维南原理对单个连接件的受力范围进行假定，并将受力薄弱部位作为控制截面进行单个连接件区域抗弯刚度的计算，横板向抗弯刚度则为各连接件抗弯刚度之和，而顺板向抗弯刚度不考虑板缝的影响，连接件区域的示意图如图20所示，取1-1 截面为控制截面，图20 中b为单个连接件受力范围宽度，c为开孔板在板缝截面宽度；

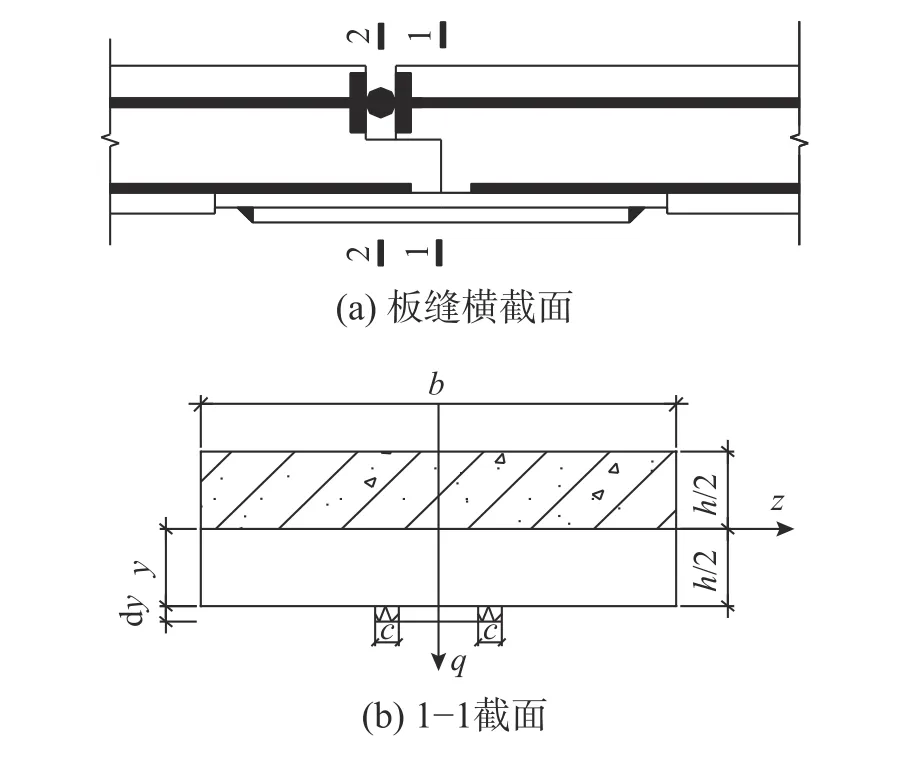
图20 横板向板缝截面示意图Fig. 20 Sketch of sections in transversal slab

2)考虑开孔板的变形以及锚筋的滑移变形，按照受力等效的原则计算出盖板式连接件钢材的等效弹性模量，从而进一步提高单个连接件区域抗弯刚度的计算精度，盖板式连接件受力变形的等效示意图如图21 所示；

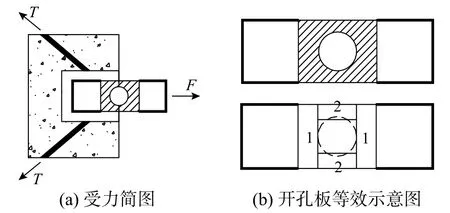
图21 盖板式连接件示意图Fig. 21 Schematic diagram of cover-plate connector

3)按照正交双向异形板自由振动的动力学理论推导出四边简支条件下矩形薄板的自振频率计算公式，将计算得到的横板向、顺板向抗弯刚度等参数代入即可求得DCPCD 的自振频率。

各试件自振频率理论计算值与实测值对比如表9 所示。由对比可知，3 个试件的自振频率理论计算值和试验值吻合良好，表明正交各向异性双向板振动理论能较好地应用于DCPCD 基频的计算。

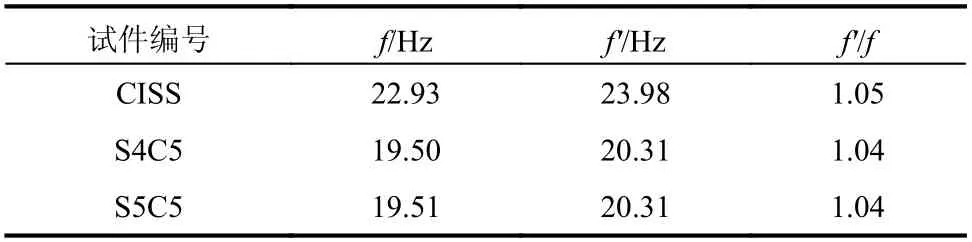
表9 自振频率计算值与试验值对比Table 9 Comparison of fundamental frequency between calculation and test results

4.2 人行荷载下峰值加速度的理论计算

由于DCPCD 双向异性的特性，应按照正交双向异性四边简支矩形薄板的受迫振动理论计算振动加速度，则在简谐力作用下的振动微分方程参见式(3)。取振型函数为：

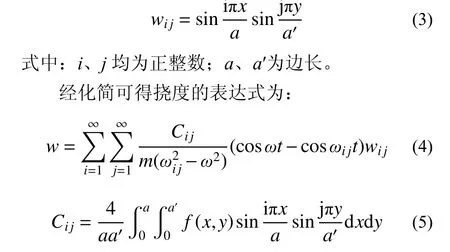
式中：ω为简谐力圆频率；ωij为楼盖自振圆频率。

因为人行荷载频率通常在3.5 Hz 以下，低于楼盖的固有频率，因此只考虑与荷载频率较接近的前三阶振型对挠度的贡献[28]。由于挠度最大点位于楼盖中心，亦是第二阶、第三阶振型的节点，因此只需考虑一阶振型的情况。对一阶振型的挠度表达式求二阶导数可得加速度为：

式中：M为人体重量；Te为单步落足荷载周期，Te=1/0.76fs；Bk为与步频fs相关的傅里叶系数，考虑前三阶即可，B1=-0.0698fs+1.211，B2=0.1052fs-0.1284，B3=0.3002fs-0.1534；标准单步落足荷载示意图见图 22，虚线为足重叠时间。

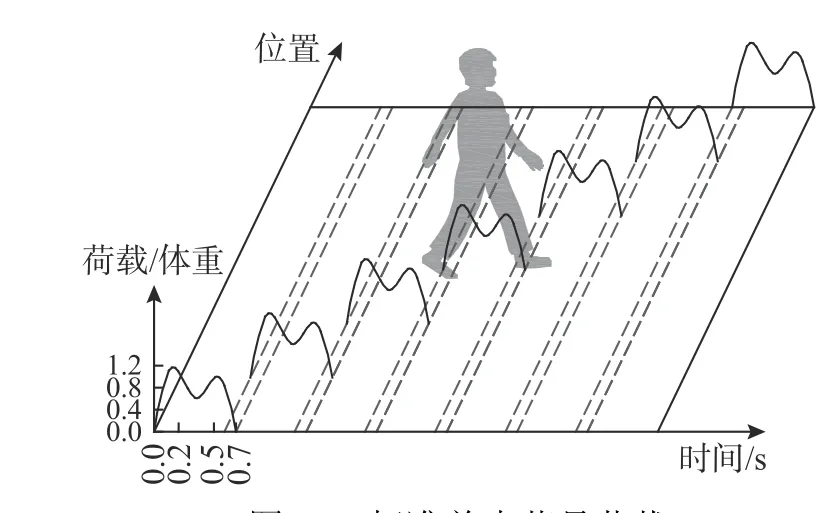
图22 标准单步落足荷载Fig. 22 Standard single-footfall forces

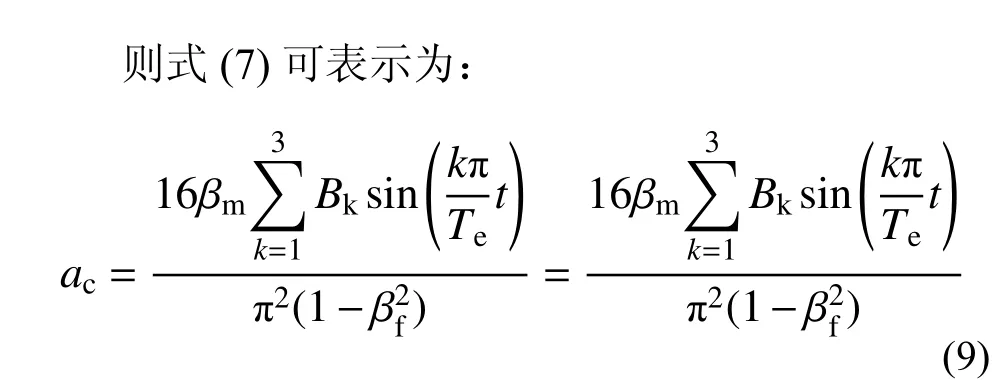
式中：βf=f/f11称为频率比，表示人行荷载频率与楼盖基频比值；βm=M/m称为质量比，表示人体质量与楼盖质量比值。

通过对正交双向同性四边简支矩形薄板化简计算也可得到式(9)，故现浇试件也可以按该式计算峰值加速度。行走荷载为移动荷载，荷载的大小、作用点时刻都在发生变化，通常采用折减系数来消除作用力的变化带来的影响，一般为0.7～0.9[30]，通过实测结果与理论计算结果对比分析可得到适用于各试件的参数取值，本文中试件CISS 取0.8，试件S5C5 取0.9，试件S4C5 不进行折减。参考前述试验现象，相同荷载条件下试件S4C5 的峰值加速度最大，试件S5C5 的峰值加速度次之，试件CISS的峰值加速度最小。其原因为现浇楼盖整体性和竖向刚度较好，同荷载条件下的振动加速度最小，因此折减系数取最小；DCPCD 由于板缝的存在致使楼盖整体性和竖向刚度降低，同荷载条件下的加速度大于现浇楼盖，因此折减系数较大，而试件S4C5 由于板缝位于跨中，使跨中板缝处加速度增大，因此不折减。

单人标准行走工况下的峰值加速度的理论值与实测值见表10。由表10 可知：理论值与实测值吻合良好，所提出的理论计算方法可较好地进行人行荷载下楼盖竖向振动加速度的计算。

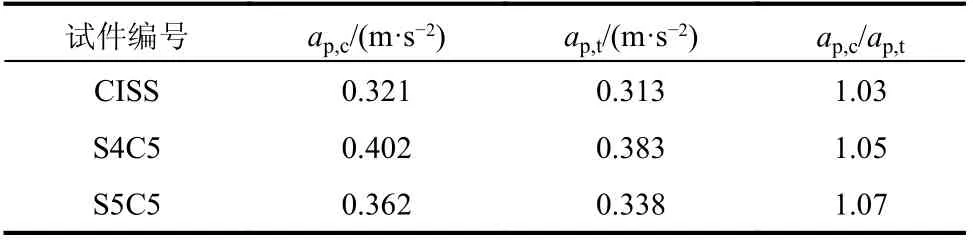
表10 单人标准行走下峰值加速度计算结果与试验结果对比Table 10 Comparison between calculated and test peak accelerations under single walking

5 振动舒适度的评价

5.1 不同支座约束条件下的舒适度评价

实际工程中常见四边支承的混凝土楼盖，其支承形式主要有四边固支、三边固支一边简支(边跨)和两临边固支两临边简支(角跨)等形式。不同支承方式对楼盖自振频率和挠度影响较大，进而影响楼盖的振动加速度。可采用支座影响系数来反映支座形式对楼盖的影响[31-32]，文献给出了各支承条件下楼盖自振频率及最大挠度的计算方法，四边简支条件下支座影响系数见表11。

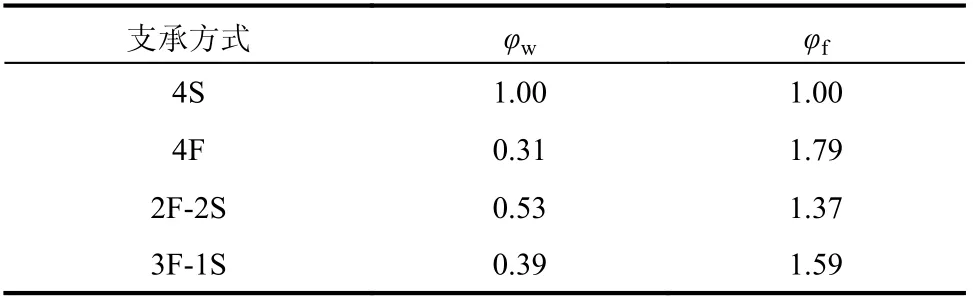
表11 支座影响系数Table 11 Support influence coefficients

考虑支座影响系数的楼盖自振频率和峰值加速度见表12。

由表12 可知：1)三种工况下，自振频率均大于3 Hz，满足舒适度要求；2)四边嵌固条件下DCPCD 与现浇楼盖均满足加速度小于0.15 m/s2的舒适度要求，三边嵌固一边简支条件下只有试件S4C5 不满足舒适度要求，两临边嵌固两临边简支条件下均不满足舒适度要求。

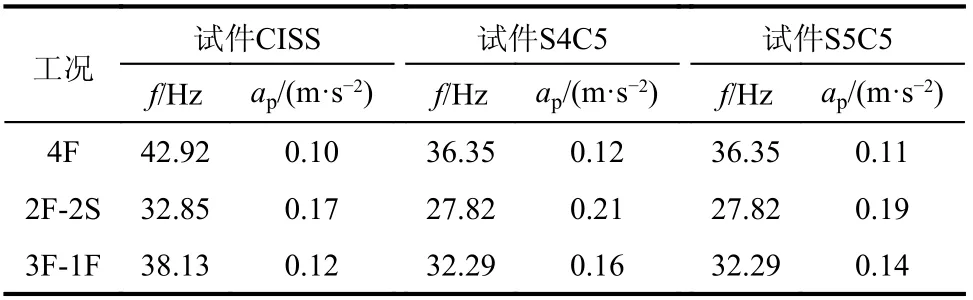
表12 不同支撑条件下的基频与峰值加速度Table 12 Fundamental frequency and peak acceleration under different support conditions

由式(9)可知，人行荷载与楼盖的质量比和频率比都是影响峰值加速度的因素，二者与楼盖峰值加速度关系详见图23。

图23 中横轴为频率比βf，纵轴为质量比βm，曲线为舒适度曲线，曲线与坐标轴包围的内部为满足舒适度要求的情况。由图23 可知，βf越小，舒适度曲线的斜率就越接近0，此时提高楼盖的自振频率并不能有效改善舒适度，可通过增加楼盖自重降低βm从而减小楼盖峰值加速度，增加板厚、增大跨度均可降低βm以达到楼盖振动舒适度的评价标准。而当βf接近1 时，即荷载频率等于楼盖自振频率，发生共振现象，此时质量比接近0 才可满足舒适度标准，因此，应限制楼盖自振频率下限，避免在实际应用中与人行荷载发生共振。

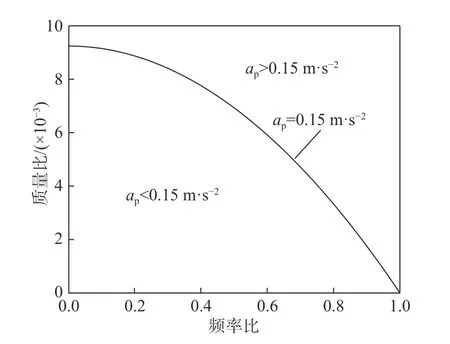
图23 质量比-频率比关系曲线Fig. 23 Relationship between mass ratio and frequency ratio

5.2 基于舒适度的楼盖横纵向刚度比取值范围

通过改变楼盖跨度l、横板向与顺板向刚度比(以下简称横纵向刚度比φ)可分析DCPCD 自振频率和峰值加速度的变化规律。

楼盖板厚h约为跨度的1/35，横纵向刚度比φ分别取0～1.0。对于大开间楼盖，DCPCD 体系以空心或夹层预制板为基本构件，空心率为25%，顺板向截面惯性矩和等效弹性模量参照规范[33]进行计算：

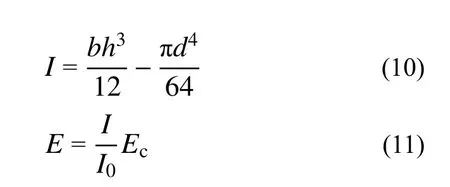
式中：b为计算单元长度；d为空心半径；I为计算单元空心截面惯性矩；I0为计算单元实心截面惯性矩；Ec为混凝土弹性模量。

以两临边简支、两临边嵌固的现实工程中最不利情况(角跨)为例，分析单人标准行走工况下4.2 m～9 m 跨度空心DCPCD 自振频率与峰值加速度响应，计算值详见表13，由表13 可知：

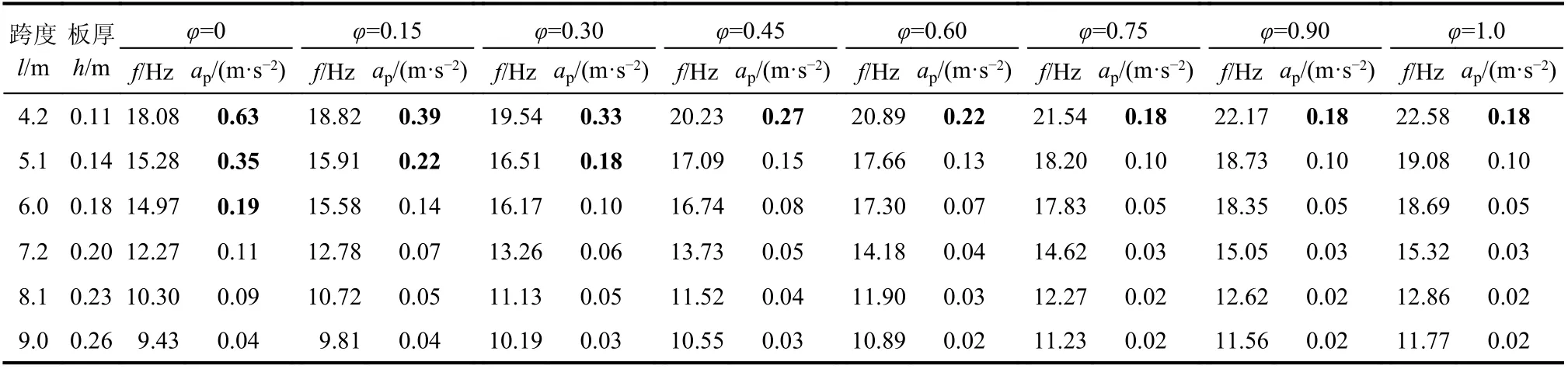
表13 4.2 m～9 m DCPCD 自振频率及峰值加速理论计算结果Table 13 Calculation results of natural frequency and peak acceleration for 4.2-9 m span DCPCDs

1)随着楼盖跨度的增大，人行荷载与楼盖质量比减小，自振频率和峰值加速度均呈下降趋势。

2)横纵向刚度比对楼盖自振频率的影响较明显，φ由0～1，DCPCD 自振频率最大增加24.89%；φ由0.75～1，DCPCD 的自振频率最大仅增加4.83%，且9 m 跨度DCPCD 的φ为0 时依然满足自振频率大于3 Hz 的控制标准，因此，只考虑自振频率的条件下，φ的取值可为0～0.75。

3)横纵向刚度比对楼盖峰值加速度的影响可分区段讨论，当φ＞0.75 时峰值加速度变化较小，提高φ对峰值加速度影响不大；当φ<0.75 时峰值加速度变化较大，与跨度关系密切；当φ>0.3 时，除4.2 m 跨度楼盖外，其他情况均满足基于加速度的舒适度要求。DCPCD 跨度不大于4.2 m 时，即使φ=1.0 也不满足舒适度要求；5 m跨度时，φ需达0.45；6 m 跨度时，φ需达0.15 左右；当跨度大于等于7.2 m 时任意刚度比下均满足舒适度要求。

4)峰值加速度与荷载和楼盖的质量比有关，通常小跨度楼盖更易出现峰值加速度较大的情况(图22)，使加速度不满足舒适度规范。对于较小跨度楼盖，可以采用实心预制板或者加强四边约束的方法。比如，对于4.2 m 跨度DCPCD，采用实心构件在两临边简支、两临边嵌固条件下，当φ达到0.30 时峰值加速度为0.14 m/s2，满足舒适度要求；采用空心构件在三边固支一边简支条件下，当φ达到0.73 时峰值加速度为0.15 m/s2，满足舒适度要求。

综上，基于楼盖竖向振动舒适度标准，常见矩形布置的DCPCD 横纵向刚度比φ的建议取值范围为0.3～0.75。设计时，可根据DCPCD 的平面内刚度、竖向承载力要求选择合适的φ值，而后根据φ值确定板缝连接件的规格和数量，从而完成对DCPCD 的设计。