砂土统一本构模型研究及其三维数值实现

王子珺，赵伯明

(1. 北京交通大学城市地下工程教育部重点实验室，北京 100044；2. 北京交通大学土木建筑工程学院，北京 100044)

相关研究表明砂土的变形性质依赖于砂土密度以及剪切过程中所受的围压大小[5-7]，具体表现为松砂具有剪缩特性而中密砂则具有剪胀特性。为统一反映砂土密度和所受围压对砂土变形特性的影响，Bean 和Jefferies[5]首先提出通过一个状态参数来反映这两者的耦合作用。状态参数ψ =e-ec，即当前有效平均正应力下，实际孔隙比e与临界状态孔隙比ec之差。临界状态线定义为剪切过程中砂土的体应变增量为0，而偏应变增量为无穷大的一个状态。对于砂土的本构模型，相关研究[8]表明其e-p′平面的临界状态线更适合于非线性形式描述，即：

式中：eΓ和λc分别为临界状态线的截距和斜率；p¯=p′/pa为有效应力与大气压之比； ξ为常数，上述模型也得到相关学者的采纳与应用[3,9-11]。当ψ ＞0时，当前实际孔隙比大于相同压力下的临界孔隙比，材料处于松散状态，如图1 中A 区域所示；当 ψ ＜0时，当前实际孔隙比小于相同压力下的临界孔隙比，材料处于密实状态，如图1 中B 区域所示。 ψ值越大，材料越松散， ψ值越小，材料越密实。图2 为根据式(2)所建立的几种不同砂 土(Toyoura 砂、Tung-Chung 砂、Fuji River 砂)的临界状态线，其中， ξ建议取为0.7[8,12]。

图1 状态参数与临界状态线Fig. 1 State parameter and critical state line

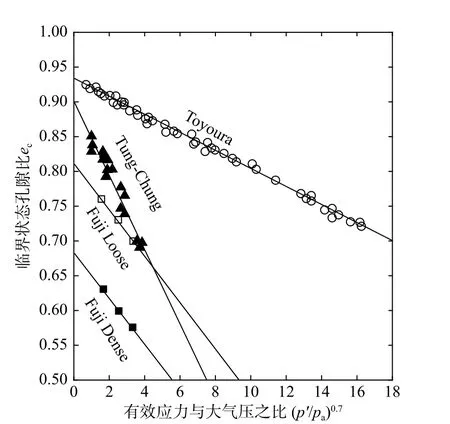
图2 几种不同砂土的临界状态线Fig. 2 Critical state lines of several different sandy soils

基于广义塑性理论与临界状态概念，Ling 和Yang[4]建立了一个砂土的本构模型，通过一组参数统一考虑不同初始密度与不同围压条件下砂土的应力-应变关系，但是该模型仅限于二维p′-q平面问题的求解。因此，本文在该方法的基础上，将模型推广应用于三维p′-q-θ空间问题的求解，使之可以考虑应力洛德角 θ的影响，从而反映三维应力状态下土的变形和强度特性。为了能够利用有限元软件前后处理方便、计算稳定性与精度高等优点，通过ABAQUS 提供的用户自定义材料子程序UMAT，基于Fortran 语言编制了上述改进的三维砂土模型的接口程序，实现该弹塑性本构关系，进而分别通过3 种砂，即Toyoura 砂、Fuji River 砂和Tokachi 砂的三轴排水剪切试验结果对模型的有效性进行对比验证。研究成果可进一步应用于相关岩土工程的数值分析，为岩土工程分析提供更加快捷实用的解决方案。

1 基于广义塑性理论和临界状态的砂土弹塑性模型

为了将状态参数引入广义塑性理论，对建立模型所需要的主要塑性参数，包括：剪胀性、塑性流动方向、加载方向和塑性模量等进行相应修正。

1.1 弹性性质

式中，G0和K0分别为弹性剪切模量与弹性体积模量。

1.2 剪胀性与相变转换

颗粒材料的剪胀性是砂土体积与形状变化之间的耦合现象[16]，应力剪胀方程描述了塑性体应变和塑性剪应变之间的关系：

1.3 塑性流动法则

1.4 加载塑性模量

2 砂土本构模型的二次开发与验证

2.1 用户自定义材料子程序UMAT 与坐标转换

针对非线性问题，通过ABAQUS 软件提供的用户自定义材料子程序UMAT(Use-defined-Material Mechanical Behaviour)与 ABAQUS/Standard 主求解程序的接口对接实现与ABAQUS 的数据交换，完成有限元数值计算。UMAT 子程序通过ABAQUS 主程序传入应变增量以及当前已知状态的应力、应变及其他与求解过程有关的变量。基于本构方程，通过迭代计算获得真实应力以及弹性、塑性应变，从而更新应力增量和状态变量，通过DDSDDE 数组提供材料本构模型的雅克比(Jacobian)矩阵 ∂Δσ/∂Δε，即应力增量对应变增量的变化率[19-20]，供主程序进行Newton-Raphson非线性迭代。

2.2 三轴试验模拟与验证

基于ABAQUS 提供的UMAT 子程序接口，使用Fortran 语言编制了上述改进的三维砂土本构模型，通过有限元模拟三轴试验并与3 种砂(即Toyoura 砂[21]、Fuji River 砂[22-23]以及Tokachi 砂[24])的试验结果进行对比，以验证模型的有效性。模拟的有限元模型如图3 所示，计算网格采用C3D20RP型。由于本研究旨在模拟验证常规三轴的应力-应变关系，因此，无需建立圆柱形试样模型[25]。

图3 计算模型Fig. 3 Computational model

提出的模型共需要12 个参数，分别为弹性参数(G0、K0)、临界状态线参数(eΓ、λc)、剪胀性参数( α、Mg、mg)、塑性流动参数(Mf、mf)、加载模量参数(m0、HL0、mb)。对于Toyoura 砂和Fuji River 砂，参数G0、K0、eΓ、λc、Mg、HL0、α由文献[4]获取；对于Tokachi 砂，上述参数由文献[24]获取，其余各项参数可分别通过第2 节中相关公式求得。此外，单位大气压力pa取为100 kPa。因此，上述UMAT 中的模型参数数组PROPS 共包括12 个分量，Toyoura 砂、Fuji River砂以及Tokachi砂的参数值见表1。

表1 统一广义塑性模型参数Table 1 Parameters of unified generalized plasticity model

由于用于存储与解有关的状态变量的数组需要不断更新，将每一步的结果作为下一步的初值，因此，还要设置相应的状态变量数组STATEV。在初始分析步(Initial)后定义2 个分析步，Geostatic(地应力)和Load(加载)。其中，Geostatic 分析步赋予初始围压，Load 分析步模拟施加轴向荷载过程。分别约束底面(1-2-3-4)以及侧面(1-4-8-5)、(1-5-6-2)3 个面上的法向平移自由度以及另外两个方向的旋转自由度，对其它3 个面施加初始围压。然后在模型顶面按照位移控制施加竖向荷载，直至模型轴向应变达到ε=25%。采用ABAQUS/Standard中自动划分时间增量步长的方法，可以为UMAT输送较为合理的 Δε值。最后提交任务，读取包含UMAT 子程序的Fortran 文件，进行后处理。

根据调整的模型参数结合有限元计算结果对砂土弹塑性本构模型二次开发的准确性和有效性进行验证。对于Toyoura 砂，图4 和图5 分别表示利用100 kPa 和500 kPa 下不同孔隙比(e=0.831～0.996；e=0.810～0.990)的三轴排水剪切试验结果(图例符号表示)与模拟计算结果(曲线表示)的对比。

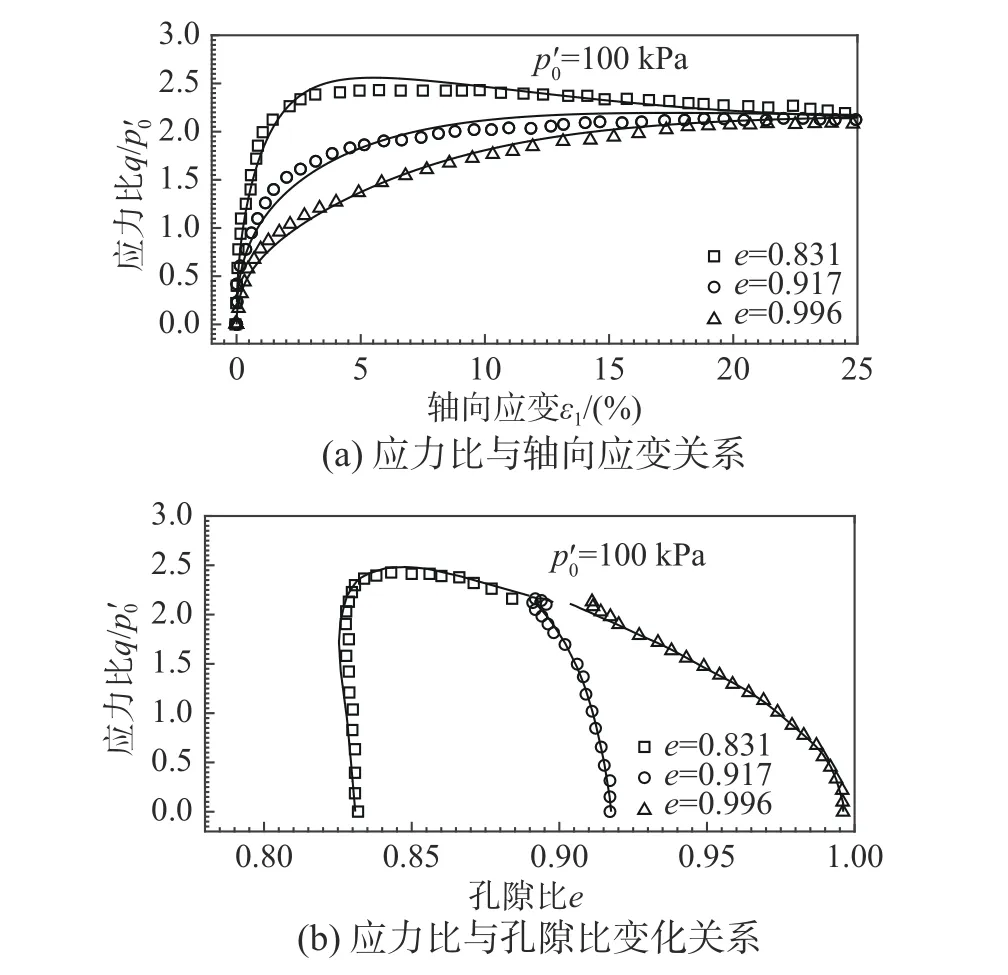
图4 p′0=100 kPa 下Toyoura 砂三轴排水剪切试验结果(图例符号)与有限元计算结果(曲线)对比Fig. 4 Comparison between experimental results (symbols)and finite element analysis results (curves) on drained triaxial responses of Toyoura sand with initial confining pressure p′0=100 kPa

由图4 和图5 可知，根据建立的ABAQUS 有限元模型得到的曲线与试验结果吻合度很高。对于砂土的排水剪切试验，其力学特性因初始孔隙比和围压不同而有所变化。在相同的围压下，当初始孔隙比较大时(e=0.996/0.990)，在剪切过程中试样一直表现为剪缩状态，应力-应变曲线一直表现为硬化；当砂土的初始孔隙比较小时(e=0.831/0.810)，试样表现为先剪缩后剪胀，且剪缩量较小而剪胀量较大，应力-应变曲线表现为初始硬化，达到峰值强度以后表现为少量的软化；对于中密度砂(e=0.917/0.886)，应力-应变关系则介于两者之间。尽管试样的初始孔隙比不同，随着应变的不断增加，应力最终趋于稳定值。试验结果与预测结果对比显示，模型能够很好地预测砂土体积变化趋势，反映出砂土的力学特性。

图5 p′0=500 kPa 下Toyoura 砂三轴排水剪切试验结果与有限元计算结果对比Fig. 5 Comparison between experimental results (symbols)and finite element analysis results (curves) on drained triaxial responses of Toyoura sand with initial confining pressure p′0=500 kPa

对于Fuji River 砂，图6 和图7 分别表示利用松散状态(e=0.747～ 0.751)和密实状态(e=0.496～0.519)下三轴排水剪切试验结果(图例符号表示)与模型结果(曲线表示)的对比。

对比图6 和图7 可知，对于松砂，当初始围压较大时(p=294 kPa)，试样一直表现为剪缩；当初始围压较小时(p=98 kPa)，试样表现为先剪缩后剪胀；当初始围压p=196 kPa 时，试样变形介于二者之间。对于密砂，在考察的三种围压条件下均表现出先剪缩后剪胀性质，初始围压越小的试样剪胀量越大；随着围压的增大，砂土的强度和刚度都明显提高，密砂的剪切特性有像松砂转变的趋势。

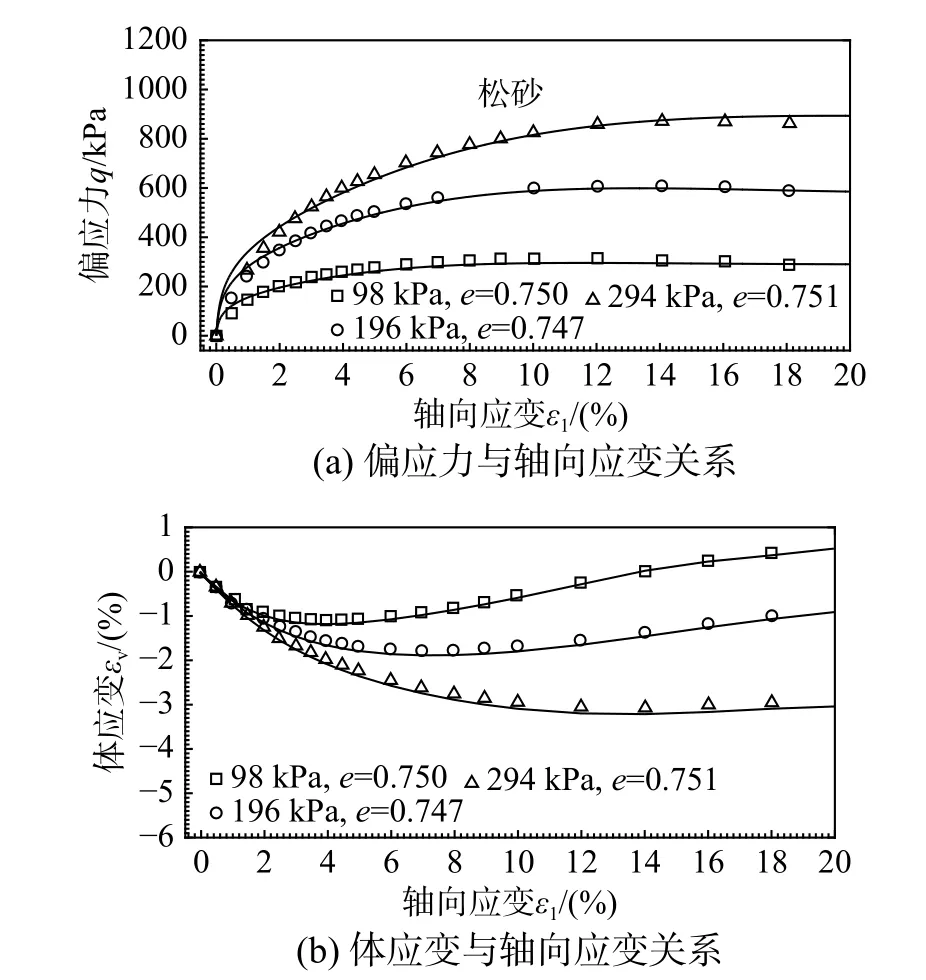
图6 松散状态下Fuji River 砂三轴排水剪切试验结果(图例符号)与有限元计算结果(曲线)对比Fig. 6 Comparison between experimental results (symbols)and finite element analysis results (curves) on drained triaxial responses of loose Fuji river sand

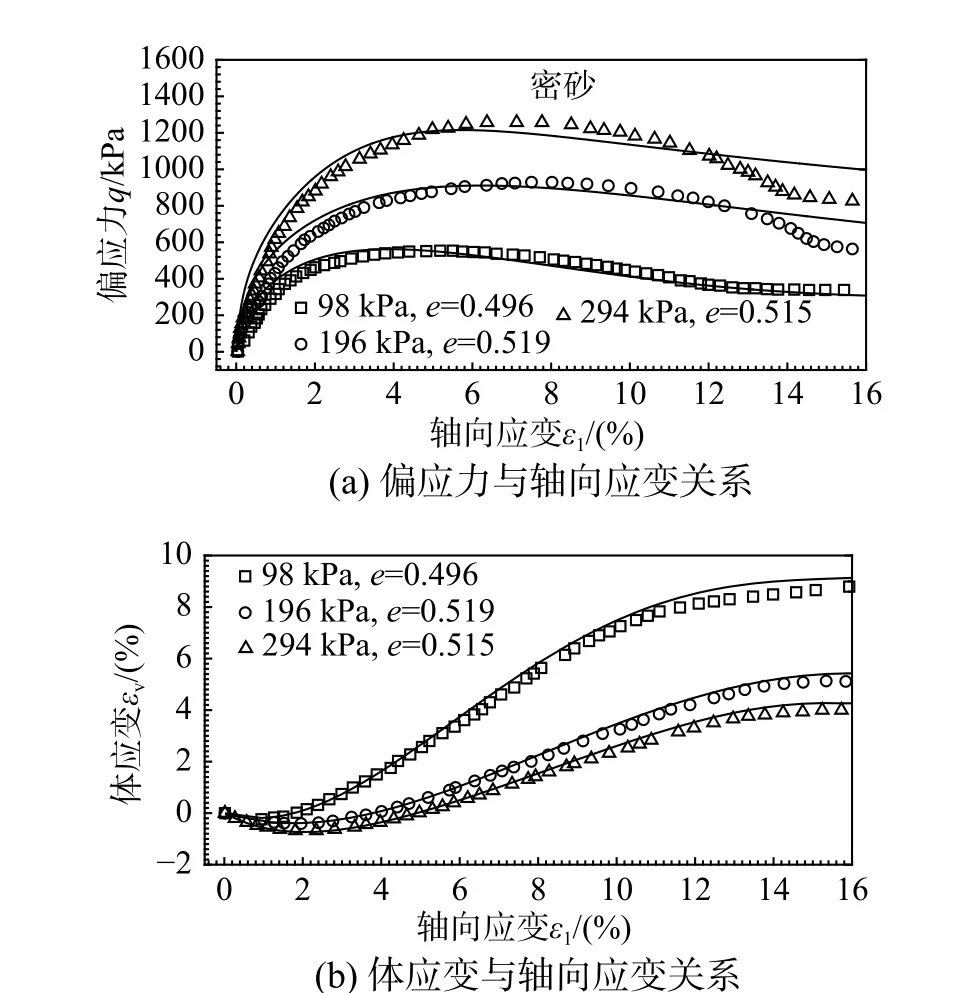
图7 密实状态下Fuji River 砂三轴排水剪切试验结果(图例符号)与有限元计算结果(曲线)对比Fig. 7 Comparison between experimental results (symbols)and finite element analysis results (curves) on drained triaxial responses of dense Fuji river sand

同样，根据建立的ABAQUS 有限元模型得到的偏应力与轴向应变曲线以及体应变与轴向应变曲线与试验结果吻合程度很高，表明有限元计算结果可以反映围压和砂土初始密度对应力-应变的影响，模型能够准确描述砂土体积的变化趋势。

对于Tokachi 砂，图8 和图9 分别表示利用70 kPa 和30 kPa 下不同孔隙比(e=1.01 和e=0.832)三轴排水剪切试验结果(图例符号表示)与模型结果(曲线表示)的对比。

图8 中密Tokachi 砂(e=1.01)三轴排水剪切试验结果(图例符号)与有限元计算结果(曲线)对比Fig. 8 Comparison between experimental results (symbols)and finite element analysis results (curves) on drained triaxial responses of medium dense Tokachi sand (e=1.01)

图9 密实Tokachi 砂(e=0.832)三轴排水剪切试验结果(图例符号)与有限元计算结果(曲线)对比Fig. 9 Comparison between experimental (symbols) and finite element analysis results (curves) on drained triaxial responses of dense Tokachi sand (e=0.832)

同样，模拟结果能够很好地反映试验结果。当初始孔隙比较大时(e=1.01)，对于所受初始围压较大的试样，在剪切过程中一直表现为剪缩，而对于所受初始围压较小的试样则表现为先剪缩后剪胀；当初始孔隙比较小时(e=0.832)，两种围压下的试样均表现出一定程度的先剪缩后剪胀现象。

上述结果表明有限元计算结果可以反映围压和砂土初始密度对应力-应变曲线的影响。由于砂土应力-应变之间不成单值函数关系，因此，反映土体的数学模型一般形式复杂难于准确，而本文基于现有大型有限元软件ABAQUS 平台进行二次开发，可以有效利用其强大的非线性有限元分析功能及优秀的前后处理界面，使开发的砂土统一本构模型能够进一步应用于相关岩土工程的数值分析，为所涉及的复杂工程问题提供更加快捷实用的解决方案。

3 结论

本文基于广义塑性理论与临界状态概念，研究提出了一个统一三维砂土本构模型，工作要点及结论如下：

(1)该模型可通过一组参数实现砂土由压缩至剪切过程中状态参量的统一表述，且这些参数均能够通过常规土工试验获得。基于ABAQUS 提供的用户自定义材料子程序UMAT 接口实现了该弹塑性本构关系，同时可以结合软件自动步长搜索功能，具有很好的稳定性和较高的计算精度。

(2)分别利用Toyoura 砂、Fuji River 砂与Tokachi 砂的剪切试验与模型模拟结果进行对比验证，结果表明有限元计算模型可以有效反映不同砂土类型在不同围压和砂土初始密度条件下的应力-应变曲线关系，能够准确描述密砂的剪胀特性与应变软化特性以及松砂的剪缩特性与应变硬化特性，从而更加真实地反映三维应力状态下土的变形和强度特性。研究成果可进一步应用于相关岩土工程的数值分析，为岩土工程分析提供更加快捷实用的解决方案。