模糊变量与随机变量组合时模糊可靠度计算方法研究
2021-11-12周建方郑鼎聪
周建方,郑鼎聪,高 冉,冷 伟
(1. 河海大学机电工程学院,常州 213022;2. 河海大学力学与材料学院,南京 211100;3. 四川省水利水电勘测设计研究院,成都 610072)
对于两变量功能函数:

式中,fR(r)、fS(s)分别为R、S的概率密度函数。其失效或安全准则是明确的,即结构要么处于安全状态,要么处于失效状态。
当R、S中有一个为模糊变量,或失效准则Z<0(或安全准则Z>0,下面仅以失效准则表示)为模糊状态时,其概率就为模糊概率。对于模糊概率(下面简称概率),有三种情况[2-3]:
1)失效准则具有模糊性,而基本变量具有随机性,即模糊事件的普通概率。对这类问题的处理,采用的基本思想就是用模糊集来描述模糊失效状态这一模糊事件A,进而利用Zadeh[4]对模糊事件概率的定义来计算其失效概率:
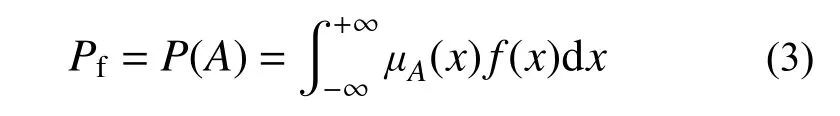
式中:f(x)为随机变量x的概率密度函数;μA(x)为模糊事件的隶属函数,表示x隶属于模糊事件A的程度。所求得的失效概率为定量。
对于这种情况的研究目前相对较为深入,建立了一套与常规可靠性指标相对应的模糊可靠性指标[5-6];对结构或零部件失效概率和可靠度计算[7-8];对系统模糊可靠性分析[9-10]等。
2)失效准则不具有模糊性,而基本变量具有模糊性,即普通事件的模糊(语言)概率。也即失效状态这一事件是确切的,而概率是模糊的,通常用语言来描述事件发生的可能性,因此,也称为语言概率。它是个模糊量[11],不是定量。
目前对于这类问题虽然有许多研究,但还没有达成共识,文献[12 - 17]提出了可能性理论来求解这类问题;文献[18]提出了基于误差原理的计算方法。
3)失效准则与基本变量均具有模糊性,即模糊事件的模糊概率。由于同时含有两种模糊性,问题较为复杂,处理变得更加困难。因此,关于该类问题的研究相对较少。
因此,对于工程中经常出现的R、S中有一个为模糊变量,失效状态为确切的,属于第2 种情况,其概率应为模糊量。不失一般性,本文假设R为模糊变量,S为随机变量。对于概率是模糊量,在工程上应用是不方便的[19]。因此,许多文献从实用的角度,提出了许多计算方法,这些方法可分成以下四类:
第一类是直接把模糊变量R转化成随机变量,从而使问题变成传统概率可靠度问题,采用式(2)计算,因而得到的概率是确定量。具体转化方法有:广义密度函数法[20]、当量密度函数法[21]、信息熵法[22-23]等。
第二类是把模糊强度R的隶属函数转化成失效模糊事件的隶属函数,从而采用式(3)计算。它也有几种方法:隶属函数面积之比法[24]、截集法[25]、直接转化法[26]、模糊数总效用值法[27]、加权面积之比法[28]。它们得到的概率也是确定量。
第三类为可能度法[16]。通常情况下,可能度法是针对R、S都是模糊变量情况下的,但文献[16]把它应用到一个是随机变量、一个是模糊变量情况。它得到的概率是模糊的。
第四类为实用计算法[29]。它的一般形式是R、S都是模糊随机变量,R为模糊变量、S为随机变量时是它的特殊情况。它得到的概率也是模糊的。
从上面可以看出,这些计算方法各不相同,自然结果也是各异。由于至今为止对于这种情况还没有一个公认的更准确的方法,因此这些方法熟优熟劣,目前没有标准,也无人对此研究。本文系统分析总结了这些方法,疏理了这些方法之间的相互关系,对R为对称线性隶属函数和正态隶属函数情况推导了有关公式,并通过例子进行了精度比较,得到了一些有益的结果。
1 模糊变量直接转化为随机变量
所谓模糊变量直接转化为随机变量,就是通过将模糊变量的隶属函数转化为密度函数,从而将模糊变量直接转化为随机变量。具体有以下几种方法。
1.1 广义密度函数法[20]
文献[20]在分析模糊变量隶属函数特性的基础上,注意到在结构工程中常见的隶属度函数形式与常见的随机变量的概率密度函数经常具有相同的类型,提出了将具有某种隶属度函数的模糊变量等价转化为具有相同类型概率密度函数的随机变量方法,即所谓的广义密度函数法。按照归一化原则,它将模糊变量R的隶属函数积分,然后将隶属函数除以积分值,作为转化后随机变量的概率密度函数:式中:μR(x)为R的隶属函数;fR(x)为R转化为随机变量后的广义概率密度函数。

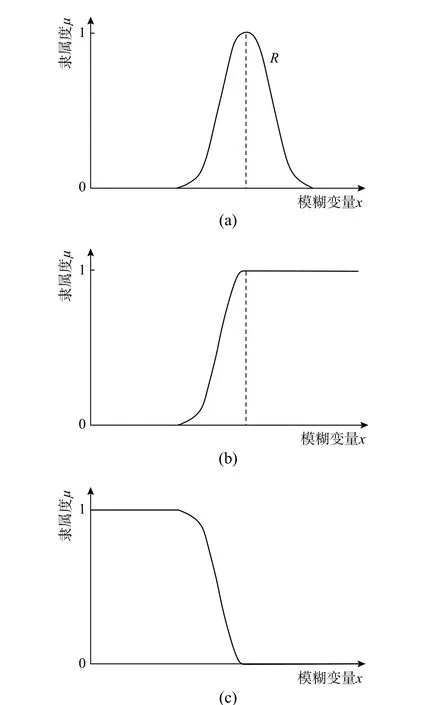
如此定义的广义密度函数fR(x),既保留了原模糊变量隶属度函数的分布信息,又满足了概率密度函数要求的完备性和非负性。由于fR(x)在自变量的取值范围内各函数值的相对大小无改变,故它对应于原隶属度函数在某值处的密度大小,仍蕴涵着原模糊变量取该值的模糊程度。因此,虽然如此转化的方法缺乏一定的理论依据,但从直观上看,还是可行的。图1 给出了模糊变量隶属度函数曲线μR(x),以及将它们按关系式(4)转化后的广义密度函数曲线fR(x)形状。

图1 隶属函数和转化后的广义密度函数Fig. 1 Membership function and transformed generalized density function
很显然,该法适用于隶属函数面积有界情况。工程中大多数都属于这种情况。
在文献[30]中,也采用了这种方法,并推导了R、S均为模糊变量时隶属函数同时为矩形、梯形、正态时可靠度的计算公式,但梯形情况式(9)有误。在文献[31 - 32]中也有类似的定义,但称为加权平均法。
对于R为对称线性隶属函数情况(图2):

图2 对称线性隶属函数和相应广义密度函数Fig. 2 Symmetric linear membership function and corresponding generalized density function

式中:m为均值;α 为分布参数。分布参数越大,模糊变量越模糊,可能取值的范围越大。
在文献[26]中给出了将密度函数转化为隶属函数的公式:

取ρ 为隶属函数的积分,则上法本质上也属于广义密度函数法。
有了式(4)后,就可以根据式(2)求失效概率,它是一个定值。
1.2 当量密度函数法[21]
文献[21]根据模糊事件A的概率P(A)可由其λ 截集Aλ的概率P(Aλ)在区间[0,1]内积分获得这一结论[33],给出了当量密度函数法。
首先对R取λ 截集,由模糊数学的λ 截集的概念, 则可得到一普通集合[aλ,bλ],在这普通集上,认为R是均匀分布的随机变量,然后按照常规可靠度方法求失效概率,再对所得概率积分(λ从0~1)得到失效概率,然后与常规可靠度计算公式(2)进行比较,得到当量密度函数式(13),从而将模糊变量转化成随机变量:

有了式(13)后,代入式(2),就可求得失效概率,它也是一个定值。
1.3 信息熵法[22]
所谓信息熵法就是根据随机变量信息熵和模糊变量信息熵相等的办法,将模糊变量转化成随机变量。该法在早期的模糊可靠度研究中应用较多[34-35],其基本思想为:
连续随机变量x信息熵定义为:

就可将模糊变量转化为随机变量。

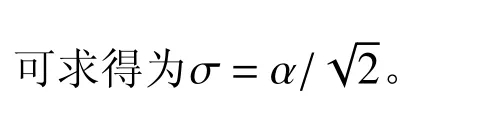
很显然,以上转化同样只能适用于隶属函数有界情况,并且一个等式,只能得到一个参量,通常根据这个等式求标准差,而对于均值,有三种做法:
1)对于隶属函数为对称型的,则将对称点值作为均值;
2)其均值等于不考虑模糊变量模糊性时的值[36];
3)在文献[36]中,按式(4)定义概率密度函数,然后根据该概率密度函数按概率方法求均值,将该均值作为转化后正态分布的均值。显然该方法存在矛盾的地方,因为既然认为转化后为正态分布,又用式(4)定义的概率密度函数去求均值,相当于同一隶属函数出现了两个概率分布。
以上转化虽保证了转换前后模糊变量与当量随机变量不确定程度的大小相等,但它是不确定性总体信息的含量,各变量与之对应函数间的映射关系并未真实保留,隶属函数和概率密度函数分别表达了自变量与之对应函数间的一一映射关系,仅按熵等价转化之后,至少损失了原有的分布信息,使转化后随机变量的分布概型不唯一。因此,这种转化处理是不严密的[20]。
2 由模糊强度的隶属函数直接构造模糊失效事件的隶属函数
虽然当R为模糊变量时,给出了其隶属函数,但它仅是变量R本身的隶属函数,并不是失效事件的隶属函数,因此不能直接代入式(3)进行计算。但有许多文献在R隶属函数的基础上,采用不同的方法构造出模糊失效事件的隶属函数,从而计算失效概率。
2.1 隶属函数面积之比法[24]
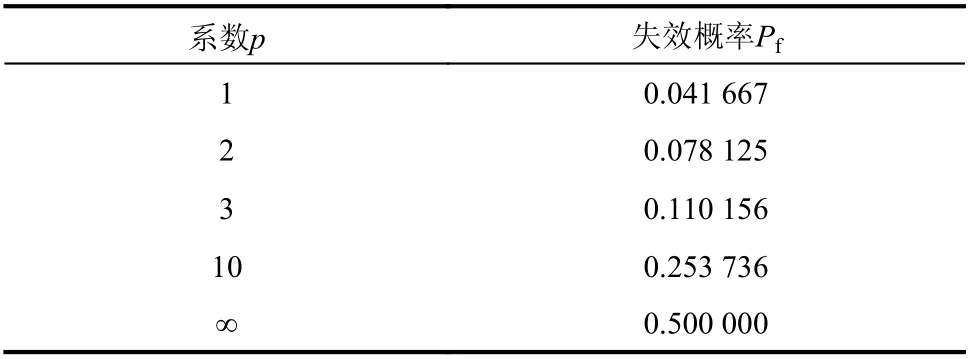
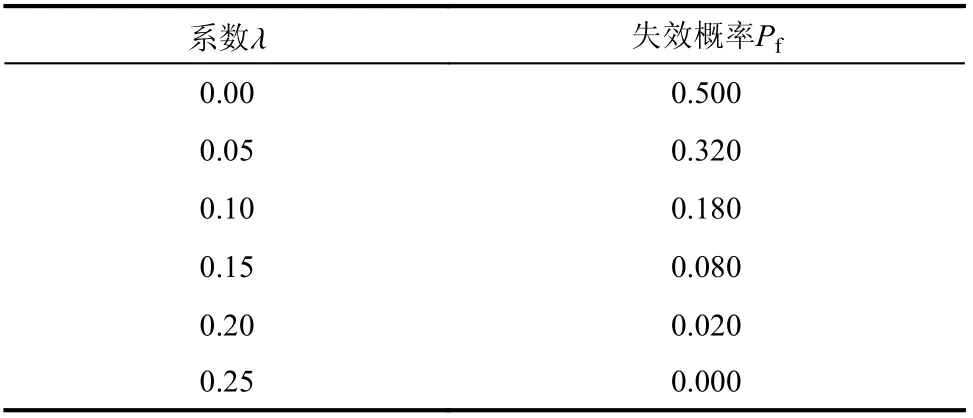
该法认为图3 中区间[xmin,S]为某种程度上的失效区,而[S,xmax]为某种程度上的安全区,可以用模糊强度的隶属函数在某种程度上的失效区的面积与整个隶属函数的面积的比值来定义模糊失效状态的隶属函数,注意这里的失效状态是指R 式中,各量意义见图3。 图3 隶属函数面积之比法Fig. 3 The area ratio method of membership function 该法本文称之为隶属函数面积之比法。当R为式(5)所示对称线性隶属函数时,可得: 求得了失效事件的隶属函数后,代入式(3),就可求得失效概率,它是一个定值。注意这里的密度函数是S的密度函数。 在文献[37]中,计算了对数正态分布应力、线性模糊强度的具体例子。 与当量密度函数法类似,同样对R取λ 截集,将模糊变量变为在普通集合[aλ,bλ]内均匀分布的随机变量,然后按照常规可靠度方法求失效概率,再对所得概率积分(λ 从0~1)得到模糊失效概率,与式(3)比较,从而可得模糊失效事件的隶属函数,本文称之为截集法。 当R为线性隶属函数,失效事件A的隶属函数: 式(24)、式(25)图形如图4所示。 图4 模糊失效事件隶属函数Fig. 4 Membership function of fuzzy failure event 代入式(3),可求得失效概率。同样,这里的失效状态是指R 在上述文献中,均是认为在截集[aλ,bλ]内R是均匀分布的,事实上这并没有理论依据。文献[43]讨论了在截集上取三种分布(均匀、线性、截尾正态)时结果的差异性,在三种分布情况中,均匀分布所算得的模糊失效概率最大。 在文献[3]中证明,若以均匀分布、线性分布或截尾正态分布为截集分布,则当模糊变量逐步收敛于随机变量时,基于截集法的可靠度将收敛于固定值,该数值只与安全准则的形式有关,而与具体结构无关,这一结果证明了常用截集分布在模型收敛性方面的缺陷和不足,因而提出了所谓的一类新的截集分布-本征截集分布,同时讨论了本征截集分布下模型的收敛性。 另外,需要说明的是,当有多个模糊变量时,每个变量的阈值λ 应不相同,不能用同一λ 值,不然会得到不正确的结果[44]。 所以,截集法的应用,受到诸多因素的制约。 所谓直接转化法,就是根据R的隶属函数,直接转化成模糊事件的隶属函数。对于图5(a)的R隶属函数,可以转化为图5(b)中的模糊失效事件的隶属函数,其余集就为模糊安全事件的隶属函数(图5(c))。这个方法本文称之为直接转化法。 图5 隶属函数转化过程Fig. 5 The transformation process of membership function 式(26)的余集即为相应模糊失效事件的隶属函数。 该法根据模糊数学理论,引入了模糊数最大集、最小集概念,给出了模糊数右效用值、左效用值和总效用值的定义,提出了模糊数的排序规则,在上述定义和模糊强度隶属度函数(主要用于求效用值)的基础上建立了模糊失效事件的隶属函数,从而进行可靠性计算。 模糊失效事件的隶属函数定义为: 式中:Ur、Ul为右效用值、左效用值;xmax、xmin是R的最大、最小值。 图6 随p 变化的模糊安全事件隶属函数Fig. 6 Fuzzy security event membership function varying with p 式(27)存在的问题是,在s=xmin处隶属函数不连续,文献[28]也指出了这点。因此,该法目前没有被广泛使用,这里作为一种思路,把它列出。 文献[28]认为影响模糊数大小有两个主要特征因素,一个是隶属函数曲线下的面积分布,即对于任一点它两侧隶属函数曲线下面积的大小;另一个是隶属函数的峰值的位置。在此基础上,将R的隶属函数转化为模糊安全状态隶属函数μA。μA由两部分组成,第一部分根据R的隶属函数的面积分布求得(式(28),图7): 图7 根据μR 的面积分布确定μA1Fig. 7 Determine μA1 according to the area distribution of μR 图8 根据Rp 的位置确定μA2Fig. 8 Determine μA2 according to the position of Rp 然后加权求和: 式中,w1、w2为权值,其值之和为1。 文中说,权值w1、w2可结合具体问题,根据经验或其他方法给定。一般情况下,隶属函数不对称程度越大,w2的值越大。 该法除权值凭经验确定外,其计算公式(29)也无多少理论依据,而且Rp的隶属函数μRP(x)如何确定,也无依据和办法,文献中说可以是正态形或对称三角形,但为何采用这两种隶属函数以及采用这两种隶属函数差别多少,也无研究,所以实际中使用很少。 当w2=0 时,实际即为隶属函数面积之比法,所以面积之比法也可看作为此法的特例。 文献[12]最早对可能性理论进行了系统研究,提出了其基本概念和理论体系。它主要针对的是R、S都是模糊变量的情况。文献[16]把它与区间可靠度方法相结合,推广到了一个模糊变量、一个随机变量情况。 首先对R取λ 截集,变成区间变量[aλ,bλ],然后求其区间可靠指标: 对不同的λ,可得相应的失效概率,从而即得模糊失效概率的可能性分布。可以看出,失效概率不是定值,是随λ 而变化的,因此是个模糊量。 文献[29]是从最一般形式开始讨论的。它首先将R、S认为是模糊随机变量,根据模糊随机变量的定义,采用λ 截集,将R、S变成随机区间: 上面列出了各种计算方法,下面对这些方法作一比较分析。 1)上面四类方法是按对变量的处理方式而分的,如果按求得的失效概率属性又可合并成两类:一类是求得的失效概率是定量,如广义密度函数法、当量密度函数法、面积之比法等价、截集法等;另一类是求得的失效概率是模糊量,有可能度法、实用计算法。 2)在第一类、第二类方法中,广义密度函数法与面积法等价[31],这从计算公式上就可直接证明。当量密度函数法与截集法相同,因为出发点是相同的。事实上对当量密度函数积分,就是事件的隶属函数。 广义密度函数与信息熵法是一致的,其定义也可从信息熵相等公式中得到,自然满足信息熵相等的要求。 3)广义密度函数法与截集法是不等价的,文献[46]中证明两者等价是不正确的。证明中先认为R转化后在区间内是均匀分布的,然后证明确是均匀分布的,来回重复。事实上,当定义密度函数后,它根据R的隶属函数是有分布的,不是常量,再认为是均匀分布是不正确的。这从后面的例子结果就可以看到。 4)直接转化法是将抗力的隶属函数直接转化为模糊安全事件的隶属函数,与面积之比法和截集法都不同。因此,在第一类、第二类方法中,本质上是3 种方法:面积之比法(广义密度函数法)、截集法(当量密度函数法)和直接转化法。图9分别给出了R为线性隶属函数和正态隶属函数情况按广义密度函数法和当量密度函数法转化后的概率密度曲线,图10 则给出了按面积之比法和截集法转化后的失效事件的隶属函数,可以看出,差别还是较大的。对于直接转化法,事实上当p=1、x 图9 两种隶属函数转化后的概率密度函数Fig. 9 Probability density function after transformation of two membership functions 图10 两种隶属函数转化后的失效事件隶属函数Fig. 10 The membership function of the failure event after the transformation of the two membership function 5)目前对一个变量是模糊变量、一个变量是随机变量的情况还没有一个明确的求解方法,但从模糊数学的角度,它的失效概率应是模糊数,因此第三类、第四类解法更符合问题的本质,可能度法结果含盖在实用计算法中。 这里采用文献[47]中的算例来说明这些方法结果的差异。 其形状见图11。 图11 算例概率密度函数和隶属函数Fig. 11 The probability density function and membership function of the calculation example 求失效概率。 1)广义密度函数法 根据式(5),可得R的概率密度函数: 代入式(2),可得失效概率Pf=0.001 373。 3)信息熵法 根据式(17),可求得模糊强度R的模糊熵为G=4.188 879,假设转化后的随机变量为正态分布, 代入式(3),可得失效概率Pf=0.002 604,与广义密度函数法的结果相同。 5)截集法 根据式(24),可得失效事件的隶属函数为: 代入式(3),可得失效概率Pf=0.001 373,与当量密度函数法结果相同。 6)直接转化法 根据R的隶属函数及式(26),可得安全事件隶属函数: 具体数值可见表1。 表1 失效概率随p 变化Table 1 Failure probability varies with p 7)可能度法 根据式(32),可得: 失效概率随的可能性分布见表2。 表2 失效概率的可能性分布Table 2 The possibility distribution of failure probability 8)实用计算法 因为R为模糊变量、S为随机变量,根据式(35),可得: 对上式去模糊化,分别采用形心法和面积法可得[19]: 形心法:Pf=0.150 000。 面积法:Pf=0.006 510。 根据文献[48],面积法是比形心法更好的去模糊化方法,因此,面积法的结果应更合理。 基于算例采用不同方法计算所得的失效概率结果,可知,广义密度法的结果与面积之比法相同,当量密度函数法与截集法相同。信息熵法与广义密度函数法相差不大,这两个方法的差别在于转化后概率密度函数前者为正态分布、后者仍为线性分布,说明本算例转化后采用正态分布是可行的。可能度法的结果含盖在实用计算法中,实用计算法的结果模糊度较大,工程实际中不易应用。在定量计算方法中,当量密度函数法(截集法)计算的失效概率最小,广义密度函数法(面积之比法)居中,直接转化法最大,且相差都较大。实用计算法去模糊化后的结果居于广义密度函数法和直接转化之间。 本文对目前计算抗力R为模糊变量、应力S为随机变量情况的模糊失效概率方法进行了系统分析总结,推导了R的隶属函数为线性、正态分布时的有关公式,并通过算例给出了具体计算结果,讨论了方法之间的相互关系,可以看出它们之间的差距较大。从理论上讲,实用计算法更符合问题的本质,但其结果工程实际中不易应用,而三个定量计算方法,结果差异又较大,因此,哪个方法更合理,还需进一步研究。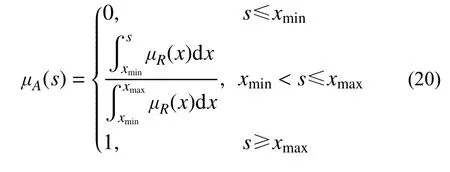
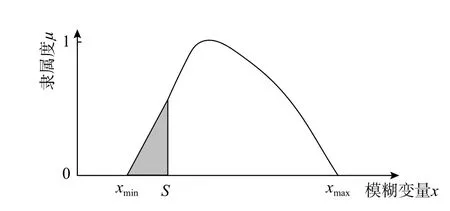

2.2 截集法[25]



2.3 直接转化法[26]

2.4 模糊数总效用值法[27]


2.5 加权面积之比法[28]




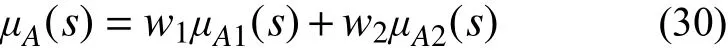
3 可能度法[16]
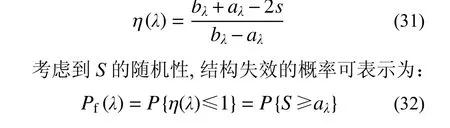
4 实用计算法[29]


5 几种方法的关系和比较


6 算例








7 结论
