多孔质静压径向轴承的理论建模与数值计算

顾延东，成 立，BÖHLE Martin，SCHIMPF Artur，袁寿其

(1.扬州大学 水利科学与工程学院，江苏 扬州 225009；2.江苏大学 国家水泵及系统工程技术研究中心，江苏 镇江 212013；3.凯泽斯劳滕工业大学 流体力学和流体机械研究所，德国凯泽斯劳滕 67663)

静压径向轴承主要依靠供压源和节流器产生承载能力，具有承载能力大、启停性能好等诸多优点，常应用于旋转机械中。节流器是其关键零件之一，有多孔质式、小孔式等。其中，利用多孔质材料加工出具有节流降压作用的轴衬，再设计供压和封装部分，就可制造出多孔质轴承。与小孔式轴承相比，多孔质轴承具有更大的承载能力、刚度等。

由于微米级润滑间隙、轴系对中、轴系旋转等原因，很难开展多孔质静压径向轴承实验研究，尤其是测试偏心率-承载能力等静特性[1-2]。目前，建立理论模型并数值求解是获得轴承特性的主要方法[3-4]。Sneck等[5]假设多孔质轴衬为一维径向可压流动，对多孔质达西方程径向积分并代入雷诺润滑方程，得到二维非线性偏微分方程，采用摄动法求解小偏心率下的静特性。Sun[6]先用Newton-Raphson法对上述方程线性化处理，再用逐次超松弛法(successive over relaxation,SOR)加速求解，指出多孔质渗透率较大时，不仅降低承载能力，而且加剧供气功耗。Majumder等[7]建立了多孔质三维流动方程并与气膜雷诺润滑方程耦合，分析了多孔质-气膜交界面速度滑移对气动不稳定性及临界质量的影响。Lee等[8]假设多孔质-气膜交界面上无速度滑移，使用低松弛因子保证可压计算的稳定性，给出了宽径比等参数的设计建议。冯凯等[9]考虑温度对气体物性及材料变形的影响，建立了带限制层多孔质轴承的温度模型，指出转速对温升的影响比载荷大。杨国栋等[10]忽略温度影响，使用非结构网格和有限体积法准确描述带槽液体润滑轴承的几何特征，获得了宽径比、偏心率对液膜压力的影响规律。商业通用CFD(computational fluid dynamics)软件是预测多孔质轴承静特性的另一方法[11-12]，但较难完成严谨合格的数值模拟，而且版权费高、计算时间长。在工程设计中，往往需要快速查找或计算零部件静特性，定制CFD程序恰好满足该需求。

本研究的主要目的是开发一种准确、快速、稳定的多孔质轴承静特性计算程序。首先，建立多孔质、多孔质-润滑膜交界面及动压润滑膜的理论模型。然后，采用数值方法求解理论模型，使用C++编写求解器PBS，并与ANSYS Fluent对比。最后，利用PBS分析供给压差和润滑剂黏度对多孔质轴承静特性的影响。

1 多孔质轴承参数

针对超临界气体旋转机械等特殊装备，采用碳纤维增强碳基复合材料[13]制造多孔质轴承并利用超临界气体润滑，如图1所示。超临界气体的密度与液体相近、黏度又明显小于液体，是值得探索的润滑剂。设计了3个多孔质轴承，相关参数如表1和图2所示。以下计算均基于表1参数。

图1 多孔质轴承Fig.1 Porous bearing

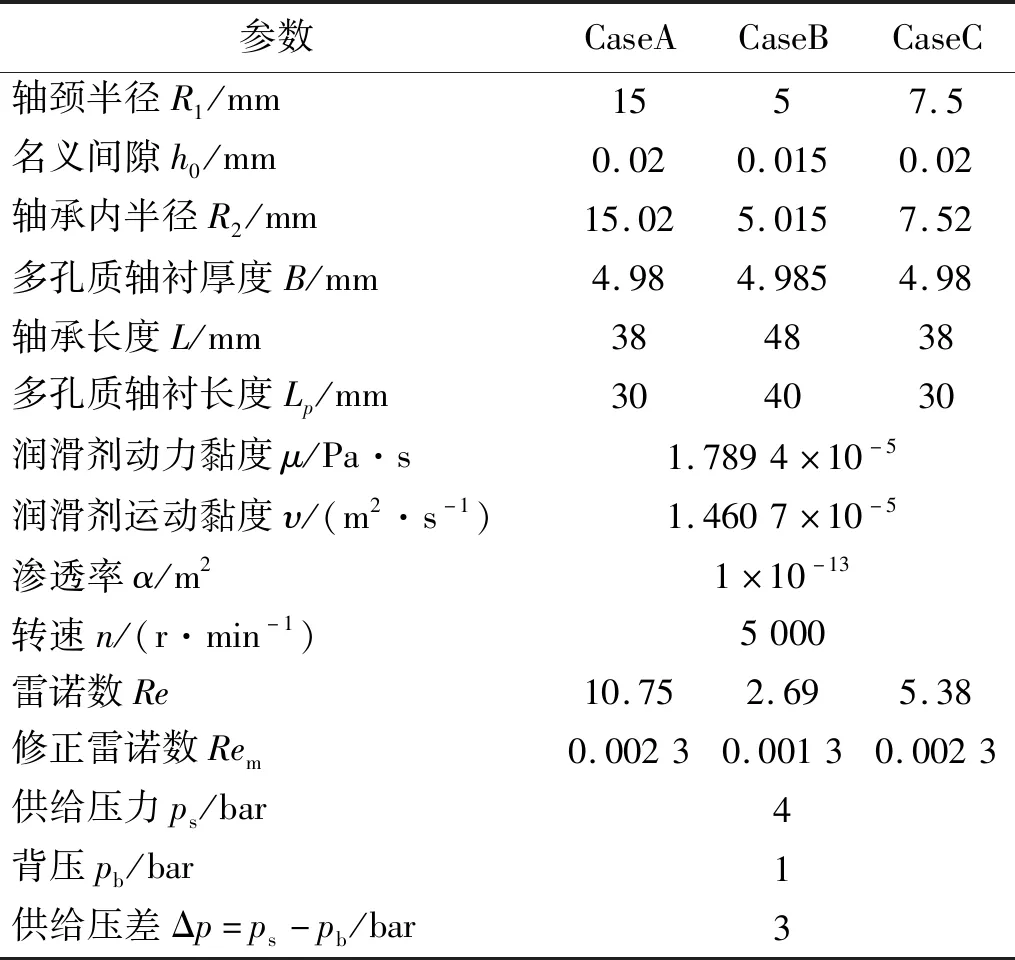
表1 轴承几何参数及运行工况Tab.1 Geometric parameters and working conditions

2 理论建模与数值计算

2.1 雷诺润滑方程

图2是多孔质轴承-转子系统示意图。采用雷诺润滑方程(reynolds lubrication equation)描述多孔质轴承润滑膜流动，该方程可以从简化Navier-Stokes(N-S)方程、再代入连续方程积分得到，或直接从黏性流体本构方程和连续方程推得[14-15]，其一般完整形式为

图2 多孔质轴承-转子系统示意图Fig.2 Diagrammatic representation for porous bearing-rotor system

(1)

式中：x，y和z分别是周向、轴向和径向坐标；h是径向间隙函数[16]；μ是动力黏度；u，v和w分别是周向、轴向和径向速度，下标a和b表示轴颈和轴衬上的分量。接下来简化式(1)。

假设轴颈为无滑移壁面，考虑剪切和挤压效应，则轴颈上的速度边界条件是

ua=R1ωcosβ≈R1ω

(2)

va=0

(3)

(4)

在等温、不可压及层流条件下，润滑剂物性参数不变，结合上述边界条件式(2)～式(4)，式(1)可简化为

(5)

2.2 多孔质轴衬流动模型

基于多孔质达西方程和连续方程，建立多孔质轴衬的流动模型。假设多孔质轴衬是三维层流，多孔质各项同性并忽略惯性阻力，采用达西方程描述其内部流动

(6)

(7)

式中：α是渗透率；i是自由标；j是哑标。将式(6)代入不可压连续方程式(7)并应用到图3坐标系，得多孔质轴衬控制方程，即圆柱坐标系下的压力Laplace方程

图3 控制方程及边界条件作用域Fig.3 Scopes for equations and boundary conditions

(8)

需要强调的是，式(8)也适用于多孔质-固体交界面。

2.3 润滑膜流动模型

基于雷诺润滑方程和多孔质达西方程，建立多孔质-润滑膜交界面及动压润滑膜的流动模型。对于多孔质-流体交界面，既有无滑移壁面处理方法，也有多种滑移壁面处理方法[17]。假设该交界面为滑移壁面，周向和轴向速度由达西方程控制，即

(9)

(10)

径向速度为

(11)

将式(9)～式(11)代入式(5)，得多孔质-润滑膜交界面控制方程

(12)

非多孔质区域的壁面条件是

ub_non-porous=0

(13)

vb_non-porous=0

(14)

wb_non-porous=0

(15)

将式(13)～式(15)代入式(5)，得动压润滑膜控制方程

(16)

式(8)、式(12)和式(16)构成了多孔质静压径向轴承的流动控制方程组，作用域如图3所示。

2.4 边界条件

上述椭圆型偏微分方程的未知量是压力，因而在边界条件设置中，需给定压力值或压力梯度或两者组合，即Dirichlet(Ⅰ)、Neumann(Ⅱ)及Robin(Ⅲ)边界条件。实际应用中，在多孔质轴衬进口供给一定压力的润滑剂，再从轴承两端排出到工作环境，因而设置进出口为压力Dirichlet边界条件。在多孔质-固体交界面上无工作介质通过，交界面法向速度(轴向速度)为0，即

(17)

则有

(18)

式(17)为压力Neumann边界条件。也就是说，多孔质-固体交界面上的压力被式(8)和式(18)同时控制。多孔质轴承的各边界条件类型如图3所示。

2.5 网格划分及离散格式

采用数值方法对式(8)、式(12)和式(16)同步求解。基于有限差分法，对计算域划分如图4所示的网格。在润滑膜和多孔质的周向及轴向上，采用均匀节点分布。在多孔质径向上，采用间距等比增长的节点分布，即Δzk+1=qΔzk。

图4 PBS计算网格Fig.4 Mesh for PBS

对控制方程中的周向和轴向一阶、二阶导数采用中心差分格式

(19)

(20)

(21)

(22)

对式(12)中的径向一阶导数采用三节点向前差分格式[18]

(23)

对式(8)中的径向一阶、二阶导数采用中心差分格式

(24)

(25)

式(19)～式(24)均为二阶精度，式(25)的精度在一阶到二阶之间，取决于公比q。对比了网格增长比率1(均匀分布，二阶精度)和1.1(近似二阶精度)的计算结果，压力几乎没有区别，因而在后续计算中都采用了1.1增长率的径向网格。交界面处细化网格对共轭传热计算非常重要，这在以后的研究中作详细说明。

多孔质-固体交界面上的压力只需式(18)的单向差分格式就可计算，这也是现有文献的处理方法。但式(18)的二阶精度、单向差分格式收敛较慢，润滑膜压力分布不连续，使用逐次超松弛法时易发散，制约了整个迭代计算的收敛速度及稳定性。如2.4节所述，多孔质-固体交界面上的压力被式(8)(Laplace方程)和式(18)(Neumann边界条件)同时控制，这里提出一种Laplace-Neumann虚拟节点法：①采用虚拟节点法处理Neumann边界条件[19]，其节点构造如图4(c)所示，利用虚拟节点pvirtual、内部节点pi,j-1,k及中心差分格式离散式(18)，得式(26)及式(27)，该处理方法为二阶精度；②采用式(21)、式(22)、式(24)及式(25)并结合虚拟节点对式(8)进行离散，然后用式(27)替换虚拟节点，则式(8)的轴向二阶导数离散形式写成式(28)并代入迭代矩阵。这个方法收敛速度极快、残差极小，更重要的是压力分布连续，符合预期的物理现象。基于上述方法，使用C++编写了快速稳定的求解器PBS.exe。

(26)

pvirtual=pi,j-1,k

(27)

(28)

3 PBS与Fluent结果对比

3.1 Fluent计算设置

对比商业通用CFD软件ANSYS Fluent 2019 R1的模拟结果，初步验证PBS理论模型和数值方法的准确性。在ANSYS Workbench中，首先使用Design Modeler建立计算域的几何模型。然后，使用Mesh模块的MultiZone策略划分六面体网格，如图5所示。在偏心方向进行局部加密，交界面网格节点完全对齐，保证了良好的网格正交性、长宽比等。通过网格无关性分析，确定3个轴承的网格节点数均为15 949 060。最后，使用Fluent对不同偏心率(E/h0)下的多孔质轴承进行模拟。在Fluent设置中，使用层流模型，采用压力进口、压力出口等边界条件，使用SIMPLE算法，各项离散精度均为二阶，收敛残差为1.0×10-6。

图5 Fluent计算网格Fig.5 Mesh for Fluent

PBS与Fluent主要差别为：①Fluent是有限体积法，PBS是有限差分法；②Fluent润滑膜的控制方程是三维N-S方程，PBS润滑膜是二维雷诺润滑方程；③Fluent中的多孔质-润滑膜交界面不能进行滑移处理，而一定条件下滑移对动压效应影响显著。在PBS中可以植入多种滑移模型，本文采用的是达西方程控制的滑移边界条件；④Fluent是将多孔质达西方程作为阻力源项，直接代入完整的N-S方程求解，渗透率大到一定程度，扩散项和达西阻力项同等显著，多孔质流动甚至从Stokes流转变为对流-扩散流动。而在PBS中，只用达西方程和连续方程描述多孔质流动，适用于Stokes流。因此，在大渗透率下Fluent和PBS不再有可比性。由于多孔质轴承是小渗透率，可对比两者。

3.2 PBS计算设置

在PBS设置中，采用迭代矩阵余量的均方根作为收敛准则，收敛精度为1.0×10-6。利用逐次超松弛法加速收敛，松弛因子为1.92。选取偏心率0.9下的承载能力(L)和偏位角(A)做网格无关性分析(坐标系如图3所示)，计算公式为

(29)

(30)

(31)

(32)

通过网格无关性分析，确定3个轴承的网格节点数均为192 000。

3.3 PBS与Fluent结果对比

图6对比了PBS与Fluent的承载能力(L)及偏位角(A)。总体而言，PBS与Fluent具有很好的一致性。在承载能力方面，PBS比Fluent高，大偏心率下(e>0.5)差值维持在2.6 N内，产生偏差的主要原因如3.1节所述。在偏位角方面，PBS比Fluent略大。动压相对于静压较小，造成偏位角较低。更重要的是，与商业通用CFD软件相比，定制CFD程序PBS具有即时仿真(instant simulation)、计算硬件要求低、可操作性强等优点，满足设计人员“one click，one result”需求。以Intel E5-2696V4 CPU为例，PBS 1核计算多孔质轴承静特性曲线需10 s左右，而Fluent 20核需4.68×104s左右。

图6 PBS与Fluent的承载能力及偏位角对比Fig.6 Comparisons of load capacity and azimuthal angle between PBS and Fluent

为进一步验证PBS，以CaseA偏心率0.9为例，对比PBS和Fluent的润滑膜压力场，如图7所示。为方便对比，在ANSYS CFD-Post中输出Fluent结果到MATLAB作图。PBS和Fluent的润滑膜压力分布高度相似。PBS压力最大值是4.006 8 bar，Fluent是4.005 2 bar，两者相差很小。由于动压效应，压力最大值高于供给压力。PBS和Fluent压力最小值均在出口，即压力边界条件1 bar。PBS高压区面积略大于Fluent，这是图6中PBS承载能力高于Fluent的主要原因之一。

图8对比了PBS与Fluent的多孔质轴衬中截面上的压力，两者非常相似。压力最大值出现在偏心方向上，PBS压力最大值是4.006 8 bar，Fluent是4.005 2 bar，与图7一致。压力最小值出现在偏心反方向上，PBS压力最小值是2.737 5 bar，Fluent是2.725 2 bar，两者相差很小。

图7 PBS与Fluent的润滑膜压力对比Fig.7 Comparisons of pressure in lubricating film between PBS and Fluent

图9对比了PBS与Fluent的多孔质轴衬中截面上的径向速度，与上述对比一样，径向速度分布也很相似。高速区出现在偏心反方向内层处，PBS和Fluent径向速度最大值均为0.159 7 m/s。在偏心方向上，径向速度趋于0，而且最低速度区略微顺时针偏移，与图8高压区偏移一致，这是由动压效应造成的。

图8 PBS与Fluent的多孔质压力对比Fig.8 Comparisons of pressure in porous restrictor between PBS and Fluent

图9 PBS与Fluent的多孔质径向速度对比Fig.9 Comparisons of radial velocity in porous restrictor between PBS and Fluent

通过对比PBS与Fluent，初步验证了多孔质径向静压轴承的理论模型与数值方法是准确可靠的。

4 结果与讨论

4.1 供给压差对静特性的影响

以CaseA为例，图10是供给压差对承载能力的影响。在同一偏心率下，承载能力随着供给压差增大而线性增大，比如供给压差2 bar的承载能力是1 bar的2倍左右，4 bar是1 bar的4倍左右。在同一供给压差下，承载能力随着偏心率增大而增大。图11是供给压差对偏位角的影响。在同一偏心率下，偏位角随着供给压差增大而减小。这是因为偏位角由动压和静压共同决定，静压随着供给压差增大，而动压几乎不变，因而动压与静压比值减小、偏位角减小。在同一供给压差下，偏心率小于0.7时偏位角几乎不变，偏心率大于0.7时偏位角略微增大。

图10 不同供给压差下的承载能力Fig.10 Load capacity under different feeding pressure differences

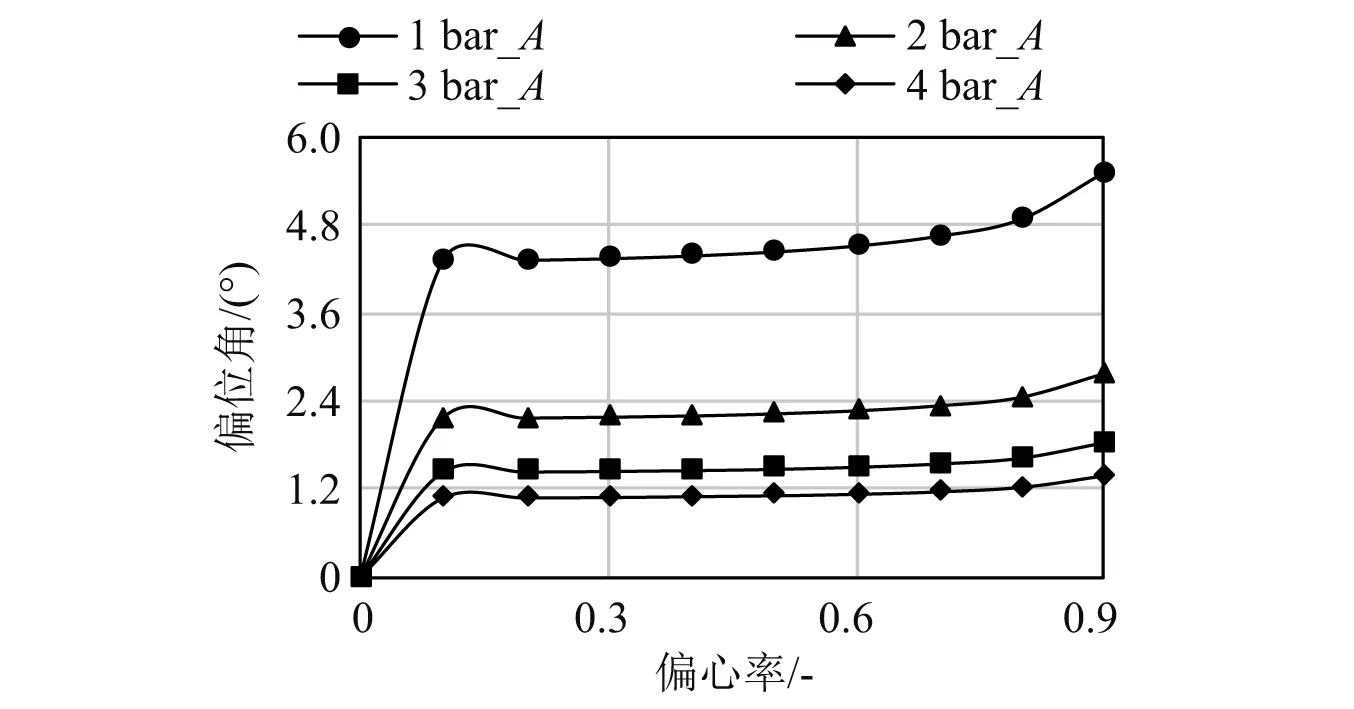
图11 不同供给压差下的偏位角Fig.11 Azimuthal angle under different feeding pressure differences

图12和13分别是供给压差对供给流量(F)和供给功耗(P)的影响。计算公式为

图12 不同供给压差下的流量Fig.12 Flowrate under different feeding pressure differences

(33)

P=FΔp

(34)

在同一偏心率下，随着供给压差增大，流量线性增大，功耗平方增大，比如供给压差4 bar与1 bar相比，压差比是4倍，4 bar的流量是1 bar的4倍左右，功耗是16倍左右。在同一供给压差下，流量和功耗最小值都出现在零偏心下。随着偏心率增大，流量和功耗逐渐增大。

图13 不同供给压差下的功耗Fig.13 Power consumption under different feeding pressure differences

4.2 润滑剂黏度对静特性的影响

以CaseA为例，黏度设置为2.20×10-5Pa·s、2.99×10-5Pa·s、3.66×10-5Pa·s及4.27×10-5Pa·s。图14是润滑剂黏度对承载能力的影响。在同一偏心率下，随着黏度增大，承载能力略微增大，偏位角近似线性增大。这是因为：①多孔质压力控制方程式(8)是Laplace方程，各项约去了黏度和渗透率，造成多孔质压力分布完全依赖于边界条件；②将多孔质-润滑膜交界面控制方程式(12)的两边乘以常数黏度，得

图14 不同润滑剂黏度下的承载能力Fig.14 Load capacity under different lubricant viscosity

(35)

图15是润滑剂黏度对偏位角的影响。对于该多孔质轴承，静压在承载能力中绝对主导，式(32)tan(FX/FY)很小时，有

图15 不同润滑剂黏度下的偏位角Fig.15 Azimuthal angle under different lubricant viscosity

(36)

所以偏位角随着黏度增大而近似线性增大。

尽管黏度对承载能力影响很小，但对功耗和流量影响很大。图16和17分别是润滑剂黏度对供给流量和功耗的影响。在同一偏心率下，随着黏度增大，流量和功耗线性减小。比如黏度4.27×10-5Pa·s与2.20×10-5Pa·s相比，黏度比是1.94，流量比和功耗比是0.52。上文从控制方程的角度分析了黏度对承载能力和偏位角的影响，即黏度对径向压力梯度影响较小，再结合式(33)和式(34)可知，流量和功耗均与黏度成反比，因此随着黏度增大，流量和功耗线性减小。与供给压差对流量和功耗的影响一样，在同一黏度下，流量和功耗最小值都出现在零偏心下。随着偏心率增大，流量和功耗逐渐增大。

图16 不同润滑剂黏度下的流量Fig.16 Flowrate under different lubricant viscosity

图17 不同润滑剂黏度下的功耗Fig.17 Power consumption under different lubricant viscosity

5 结 论

(1)针对超临界气体旋转机械等特殊装备，采用碳纤维增强碳基复合材料制造多孔质轴承并探索超临界气体润滑。基于雷诺润滑方程、达西方程和连续方程，考虑多孔质-润滑膜交界面速度滑移，建立了多孔质轴承的理论模型。引入有限差分法、变步长差分格式、逐次超松弛法，提出Laplace-Neumann虚拟节点法，建立了该理论模型的数值求解方法。使用C++编写了多孔质轴承求解器PBS，PBS与Fluent结果相近，但PBS实现了即时仿真。

(2)PBS结果表明：随着供给压差增大，承载能力线性增大，偏位角减小，流量线性增大，功耗平方增大；随着润滑剂黏度增大，承载能力略微增大，偏位角增大，流量和功耗线性减小；随着偏心率增大，承载能力、流量及功耗增大。