基于声压信号能量峭度的早期切削颤振预警技术研究

吕凯波，娄培生，谷丰收，潘文程，常宗旭

(1.太原理工大学 机械与运载工程学院，太原 030024；2.哈德斯菲尔德大学 工程与计算学院，英国西约克郡 HD1 3DH)

切削颤振是切削过程中刀具与工件之间由于存在反馈机制作用下能量补充而诱发的一种自激振动。切削加工时，由于前一转和后一转加工刀具的位移存在相位差，使得切削厚度不均匀，这种切削厚度的变化效应导致工件-刀具切削系统可能发生颤振不稳定现象[1]。颤振的发生会严重影响工件加工精度，降低刀具和机床的使用寿命，产生污染周围环境的切削噪声。因此，开展切削颤振的早期预警监测技术研究，以便在颤振来临或变得猛烈之前，采取有效的避振措施，对于保证加工稳定性具有重要的意义。

切削颤振监测的关键在于信号特征提取的准确性与快速性。早期阶段的颤振具有特征信息微弱等特点，特征参数的构造需要能够准确反映切削颤振孕育的本质与特征，还应考虑信号采集和数据处理的简便易行[2]。近年来国内外学者对颤振监测做了大量研究，提出了基于振动信号[3-8]、切削力信号[9-10]和声压信号[11-16]等的监测方法。总体来看，选用振动加速度作为判别颤振的信号源较多，这类传感器具有外形尺寸小、重量轻、便于安装，对温度、噪声或磁场的敏感度低等优点。切削力信号虽然最能直接反映切削状态，但传感器的安装通常需要对已有刀架结构进行改动，造成不便。相比而言，声压传感器安装最为便捷，且对切削工艺系统的干扰最小。

Lu等[8]采用振动加速度信号的时域方差和频谱特征作为颤振发生的综合指标，提出将实时监测数据与稳定切削特征数据库对比来识别颤振，并引入延迟机制和重叠处理技术提高了颤振识别的快速性和准确性。钱士才等[9]采用车削力信号训练了一种最小二乘一类支持向量机，建立了颤振特征数据库，提高了切削颤振在线监测准确率。任静波等[10]研究将铣削力信号的能量熵值减小作为颤振判别的依据。熊振华等[11-12]采用声压信号作为信号源，利用优化后的加权小波包熵法和在线颤振频率预估技术监测颤振，并通过实时调整主轴转速来抑制颤振。文献[13-14]通过分析原始声音信号幅值和功率谱幅值的变化来判别切削系统的稳定与颤振状态，但由于声音信号常受周围环境干扰，这种方法易造成误判。Cao等[15]对声压信号进行同步压缩变化，并利用3σ准则实现了铣削加工过程中的颤振监测。李宏坤等[16]采集了切削过程中的声压信号，基于频谱占能比的变化趋势构造特征参数实现了铣削颤振状态的识别，但由于需要时域幅值满足设定阈值才能进入频域处理阶段，所以判别的快速性难以保证。

目前，切削颤振的特征提取方法大都能准确反映颤振发生后的本质，但构造的特征参数往往对于颤振的萌生响应不够敏感。本文选用声压信号为车削颤振监测的信号源，利用小波包分解提高信噪比，提取切削加工过程目标频带的声压特征信息，引入能量峭度指标快速反映颤振孕育的开始。最后，通过切削试验对颤振监测方法进行了实际验证。

1 颤振预警监测方法

1.1 颤振声压信号特征分析

再生型颤振在实际切削过程中最为常见，切削系统从稳定到发生颤振是一个渐变的过程。研究表明，当切削系统由稳定变为不稳定时，系统的振动幅值会有明显的增大，且振动信号的频谱由宽带向窄带过渡。这里假设加工过程中的声压信号由服从高斯分布的噪声信号和简谐信号组成，模拟车削加工状态由稳定走向颤振的过渡过程，其表达式为

z(t)=A(t)sin(wct)+rand(t)

(1)

式中：t为时间序列，前一部分代表颤振发生时的振动简谐信号，其中A(t)是信号的振动幅值，它是关于时间的分段函数，ωc为颤振角频率，设为ωc=2π×200 rad/s；后一部分代表平稳车削时的随机噪声信号。分段函数A(t)表达式为

(2)

表示信号z(t)在t=1 s后，信号中出现周期颤振信号成分，且幅值将呈现指数趋势增长。为快速捕获时域信号幅值变化的信息，对比计算信号的时域方差和峭度指标两个参数，结果如图1所示。对比可见，峭度指标特征曲线对信号突变信息的响应明显快于方差曲线。实测信号中的成分往往要比此仿真信号复杂得多，且早期的微弱幅值变化极易被埋没在其他信号中，因此需要对原始信号做进一步处理。

图1 仿真信号的方差和峭度指标对比Fig.1 Comparison of time-domain variance and kurtosis index

同时，为观察仿真信号在频域内的变化情况，对信号进行时频分析，结果如图2所示。可以发现，在200 Hz颤振频率附近从0 s～3 s时间段内颜色由浅入深，代表着信号中周期成分从无到有，且幅值越来越大，预示着颤振逐步开始孕育。因此，提取目标频带的信号特征可有效避免其他频带成分的干扰。

图2 仿真信号的时频分析Fig.2 Time-frequency diagram of the simulation signal

1.2 小波包能量峭度

切削加工过程中，由于刀具切削位置、工件尺寸等参数均实时发生变化，切削系统为时变系统，其振动响应信号属于非平稳信号。小波包变换是一种多尺度的非平稳信号分析方法，具有良好的时频局部化特性和深入的数据挖掘能力。小波包m层分解将原始信号z(t)逐层分解为高频细节部分和低频近似部分，第m层可分解为2m个子频带，经重新自然排序后，第m层第i频带的频率范围为[(i-1)2-mf,i2-mf],i=1,2,…,2m，f为信号的奈奎斯特频率。对应频带的小波包系数定义为

(3)

因此，第m层第i频带的能量为

(4)

式中：K为该频带信号小波包变换离散点的总数，所有频带的总能量表示为

(5)

将特定频带能量Em,i与总能量E的比值定义为能量比R，表示为

(6)

在稳定切削阶段，各频带能量呈现均匀分布；当颤振发生时，由于颤振频率往往接近于工艺系统的固有频率，此时振动能量将主要集中在该频率附近，颤振频带能量在整个频域范围内占据主导。因此，以频带能量比值R超过一定的阈值，可作为颤振形成的有力证据。

峭度指标是信号四阶矩与二阶矩平方的比值，为一个无量纲量。当峭度指标K=3时，信号的幅值分布接近标准正态分布；K值越大，则表示信号中较大幅值数据的概率密度增加[17]。因此，基于统计理论和试验测试的数据经验设定，当峭度指标大于3时，则认为信号中含有突变振动成分。小波包能量峭度指标KE可表示为

(7)

1.3 监测方案

如前所述，已有的颤振监测方案常采用时域幅值增大作为是否进入下一特征提取的判断依据，这极可能由于早期的微弱特征信号被噪声淹没而错失及早预警的良机。为提高早期颤振监测的快速性，制定小波包能量峭度指标与能量比的颤振监测流程，以实现早期颤振孕育的预警和颤振状态的识别。流程如图3所示。

图3 车削颤振监测流程图Fig.3 Flow chart of turning chatter monitoring

(1)基于再生型车削颤振机理，分析切削加工过程中的声音信号特点，提出基于能量峭度指标的颤振监测方法。

(2)利用有限元建模仿真或锤击模态试验法，获取切削工艺系统的模态参数，以系统低阶固有频率所在频带作为目标颤振频带。

(3)实时采集并存储车削过程中的声压信号。

(4)运用数据重叠处理技术，以工件每转一圈为一个间隔，得到n个采样点的数据处理包，利用Symlets小波对信号数据进行小波包分解。

(8)

式中：fs为采样频率，Hz；Ω为主轴转速，r/min；η为数据重叠系数。

(5)计算每个数据包中对应目标频带的小波包能量。

(6)计算能量峭度指标KE和能量比R的数值大小。

(7)将目标频带的能量峭度指标与其阈值进行比较，若大于阈值3则发出颤振特征预警，认为颤振孕育开始，并进入下一步，否则返回信号采集环节，不发出颤振预警。

(8)颤振孕育开始后，将目标频带的能量比值与其阈值进行比较，本文基于先前试验数据的分析，设定能量比阈值为70%。若大于此阈值则认为颤振已经爆发，工件表面将留下明显振痕，否则不认为颤振已经爆发。

2 试验设计与数据分析

2.1 试验台的搭建

为了验证上述分析，开展轴类零件车削状态监测试验。试验台搭建如图4所示。试验在型号为JYOTI-DX200数控车床上进行，对两根结构尺寸相同的棒料进行车削试验，工件材料为AISI 1045，刀具选用DCMT11T304硬质合金刀；声压传感器型号为INV9206A，挂置于机床防护罩体内部，距离工件中点约500 mm；加速度传感器型号为YMC121A20，贴附在车刀背面。工件尺寸及切削用量如表1所示。

图4 试验台搭建Fig.4 Experimental setup

表1 试验所用切削参数Tab.1 Parameters of the turning tests

影响切削加工稳定性的因素有很多，如切削参数、支承条件、工艺系统结构参数等。切削加工过程本质为一时变过程，为了获取加工从稳定状态到颤振状态的信号数据，将工件的支承方式设计为一端固定、另一端自由；并且根据切削颤振的持续效应,在车削加工过程中，设定刀具沿卡盘向自由端方向进给。

颤振频率与工件-刀具系统固有特性有关。相比于刀具系统，悬伸的工件及其装夹系统为整个工艺系统的薄弱环节。在车削加工之前，通过力锤敲击工件的自由端给出宽频激励，同时利用加速度传感器拾取敲击点处的振动响应。图5为模态试验得到的频率响应函数曲线，显示工件系统一阶固有频率为928.1 Hz。

图5 频率响应函数曲线Fig.5 Frequency response function curve

2.2 数据初步分析

图6为切削工件Ⅰ时所采集的声压信号和振动加速度信号。观察时域波形可发现，在切削初期，切削加工状态稳定，时域信号幅值平稳；当车削到靠近工件自由端时，颤振发生，信号时域幅值明显增大，并且工件加工表面留有明显振痕。为了观察频谱的变化，分别取平稳状态时3～4 s段、颤振时12～13 s段的声音和振动加速度信号做FFT变换，结果如图7所示。可以发现，加速度信号频谱包含的频率成分通常比声压信号频谱丰富，这可能是由于两种信号的传递路径不同，高频振动信号在空气中传播要比在固体中传播衰减率大；但两种信号的频谱均能反映出主轴旋转频率fp=20 Hz、颤振频率980 Hz及其倍频等主要振动频率成分。值得一提的是，加速度信号中的901 Hz等频率成分在整个切削过程始终存在，且幅值变化不大，所以判断其可能为机床本身运转所激发的振动响应。

图6 工件I的车削加速度和声压信号Fig.6 Turning acceleration and acoustic signals of workpiece I

图7 稳定和颤振加工阶段的频谱图对比Fig.7 Comparative spectra during stable and chatter states

3 早期车削颤振预警

3.1 基于小波包能量的特征提取

图8所示为工件Ⅱ所对应的声压信号经过连续小波变换(continuous wavelet transform，CWT)后得到的时频谱。经观察，在980 Hz频率附近，时间从8～12 s亮度由暗变亮，说明在这时间段颤振已经开始孕育；另外，从12～20 s段为高亮区域，即该区域具有频率幅值大、能量集中的特点，说明在这一时间段工件颤振已成熟或形成。这与被加工工件表面存在从光滑到振纹的过渡区域的情况完全符合，同时也与理论仿真信号特点一致(见图2)，即颤振的最后爆发需要一个逐渐孕育的过程。这从另一个角度说明了可通过目标频带能量集中的变化趋势监测出颤振的孕育状态。

图8 声压信号连续小波变换时频图Fig.8 CWT results of the acoustic signals

考虑到颤振频率通常远高于主轴旋转频率且略大于工艺系统的低阶固有频率，为避免过于复杂的小波包分解又能较好地获取目标颤振频带的特征信息，根据小波包分解原理，采用Sym6小波对信号进行3层分解。为进一步了解颤振之前数据中各节点能量的变化趋势，以8～12 s时间范围为例，将时间间隔取为0.5 s，分别计算各时间段中每个节点的小波包能量比值，绘制如图9所示8×8格的三维柱状图。经过节点自然排序后，其中928.1 Hz正好落在节点3所在频带(750～1 250 Hz)，稳定车削段声压信号能量主要集中在1节点，此阶段以主轴旋转频率20 Hz信号成分为主；颤振段声压能量主要集中在3节点，此阶段以工件颤振频率980 Hz信号成分的能量为主。可以明显观察到节点3所在频带能量有激增的趋势。

图9 小波包节点能量随时间变化趋势图Fig.9 Energy trends for each wavelet packet node

3.2 监测分析结果

以工件每转一圈为一个间隔，重叠系数50%得到含600个采样点的数据处理包，对采集的声压信号实时计算3节点小波包能量值，根据式(6)、式(7)分别计算并绘制能量比值曲线R以及能量峭度指标曲线KE。图10(a)给出了车削加工过后，工件Ⅱ表面加工状态，图10(b)给出了整个加工过程采集中的声压信号以及两个颤振特征参数曲线随着车削位置变化的趋势图。在稳定加工阶段的时域幅值没有明显变化，证实了难以直接通过时域幅值变化情况监测早期微弱的颤振特征。相反能量峭度指标KE值在92 mm刻度处大于阈值3发出颤振特征预警，预示着颤振在此处开始孕育，同时观察图10(a)可发现，在65 mm刻度到92 mm刻度区间工件表面光滑无明显振纹。随后指标R值在107 mm刻度处大于阈值70%，表明颤振在此处爆发，严重的颤振将在工件表面留下明显振纹影响加工质量，同时观察工件表面加工状态证实了严重颤振现象的发生。

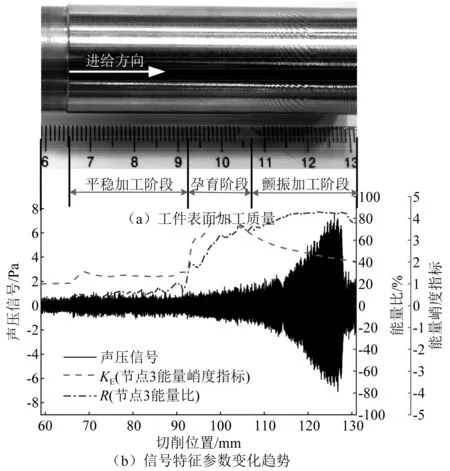
图10 工件Ⅱ的监测结果Fig.10 Verification of workpiece Ⅱ

试验结果分析表明，能量峭度指标KE能实现早期微弱颤振特征的准确识别，为颤振的抑制赢取更充分的响应时间。

4 结 论

(1)采用小波包对实时采集的声压信号进行分解，提出基于小波包能量峭度指标的早期颤振孕育状态的监测方法，实现在颤振持续发展或爆发之前及时地发出颤振预警信号，提高了颤振识别的快速性。

(2)采用切削过程中声压信号目标频带的能量比作为颤振发展状态的判别依据，获得切削颤振演变过程与信号特征之间的映射关系，增加了颤振监测方法的可靠性。

(3)利用声压传感器安装的便捷性，构建出基于声压信号的能量峭度和目标频带能量比相结合的切削状态监测指标。试验验证了该监测方法能够准确地判别出颤振从稳定到萌生再到成熟的演化过程。