传力杆偏位对机场道面水泥混凝土应力的影响

吴大林，杨玉兰

（1.勤山（上海）机场场道工程技术有限公司，上海 200092；2.四川省场道工程有限公司，成都 610081）

传力杆是机场水泥混凝土道面的重要组成部分[1]，可使道面接缝在消除温度对应力影响的同时保证正常传荷，减少道面板的过大弯沉和应力，从而保障道面的使用寿命[2]。然而测试[3]表明，使用传力杆支架或传力杆自动插入装置（DBI,dowel bar inserter）均会使传力杆产生一定程度偏位，可通过探地雷达等手段进行有效探测。文献[4-5]认为两种安装方法引起的接缝问题没有明显差异，但使用传力杆支架设置的传力杆更易产生偏位。传力杆偏位后，道面板在温度、干缩和交通荷载作用下，可能导致传荷结构的应力集中或传荷能力下降。

国内外学者对传力杆偏位的影响开展了研究。部分学者通过试验研究传力杆偏位的影响，Peng 等[6]认为传力杆角度偏转是接缝两侧50 cm 内道面开裂的主要原因。文献[3]基于试验观察到传力杆平动产生的破坏现象较少，而转动产生的破坏现象较多，并由此推知，传力杆偏位导致的传力杆传荷比例重分布并非导致道面板损坏的主要原因，道面板局部形状改变导致的应力集中才是主要原因。因此，基于单根传力杆周围应力集中的考虑，美国联邦公路管理局和美国混凝土路面协会进行了试验，提出了传力杆偏位的推荐极限值为每305 mm 传力杆偏位小于9.5 mm（3%）[7]。文献[8]通过拉拔试验提出极限值为每456 mm 传力杆偏位小于6.4 mm（1.4%）。部分学者使用有限元模拟开展传力杆偏位研究，蔡海斌[9]发现随着传力杆竖向偏位角度的增大，传力杆的传荷能力在下降，且传力杆周围有比较严重的应力集中现象。Leong 等[10]通过有限元计算了传力杆周围的应力集中，并提出传力杆偏位的容许量应该为每456 mm 小于20 mm（4.4%）。

对传力杆偏位的研究在考虑水平和竖直偏转的同时，还应考虑传力杆间的相互作用，及温度和荷载两种影响因素。由于试验只能观测到传力杆的破坏现象，对局部混凝土受力反应能力较差，但以混凝土应力为指标的有限元分析可对各种工况和各因素的影响进行直观比较。因此，从温度和荷载两种影响因素入手，通过有限元模拟研究传力杆偏位对混凝土应力的不良影响，从而对道面水泥混凝土应力集中和发生破坏的规律有较为全面的认识。

1 机场水泥混凝土道面有限元模型

有限元模型的尺寸根据机场水泥混凝土道面实际尺寸确定（单位：cm），如图1所示。模型中材料参数为：水泥混凝土为热弹性，弹性模量为36 000 MPa，泊松比为0.15，密度为2 400 kg/m3，热膨胀系数为10-5/°C；基层为纯弹性，弹性模量为1 400 MPa，泊松比为0.2，密度为2 300 kg/m3；传力杆为纯弹性，弹性模量为2×105MPa，泊松比为0.3。模型在混凝土板和传力杆接触的部分使用更密的网格。在传力杆孔口周围划分规则细密的网格，如图2所示。实际情况中，传力杆一端会做防粘处理以保证其在混凝土中可自由滑动，故模型中传力杆依据实际情况一端使用Tie（绑定）连接，另一端设置摩擦系数0.8，且交错布置。共设置14 根传力杆，其间距为0.35 m，编号1～14，其中：奇数号传力杆在受荷板中的一端为滑动端；偶数号传力杆在受荷板中的一端为固定端，在非受荷板中则相反。传力杆的偏位仅考虑偏转，偏转时中心保持不变。单根杆偏位时，取7 号传力杆进行偏位；双杆偏位时，取7 号和8 号传力杆进行偏位。传力杆的偏位方向分为水平偏位或竖向偏位，偏位角度取1.8°、3.6°、5.4°。双杆水平偏位时，考虑同向偏位和异向偏位，如图3所示。

图1 有限元模型尺寸Fig.1 Dimension of FEM model

图2 传力杆孔口周围混凝土网格划分Fig.2 Meshes of concrete around dowels

图3 双杆水平偏位示意图Fig.3 Horizontal misalignment(two-bar misalignment in different directions)

温度收缩作用的模拟方法：温度收缩引起道面板的移动，接缝会张开，温度越低接缝宽度越大。因此，温度收缩在模型中直接使用板的位移边界条件来模拟，初始接缝宽度为0，温度收缩作用后接缝宽度分别为0.33、0.67、1.00 cm。在实际情况下，温度收缩引起的缝宽通常在0.5 cm 以下，但考虑极端工况，可使结果变化规律更准确。

最大飞机荷载采用B737-800 机型，主起落架构型为单轴双轮，轮印长为0.435 m，宽为0.3 m，轮胎压力为1.47 MPa，横向轮距为0.86 m。为了使荷载作用效果更明显，有限元模型中荷载作用位置为偏位杆的正上方。

2 温度收缩作用下传力杆处混凝土应力分析

2.1 单根传力杆偏位的影响

有限元程序计算完成后，提取每个孔口传力杆和混凝土界面处的混凝土应力，水平偏位时最大主应力在板接缝处横向分布如图4所示。

图4 水平偏位时最大主应力在板接缝处横向分布（偏位角为1.8°）Fig.4 Horizontal distribution of maximum principal stress at joint with attitude angle 1.8°

从图4 中可看出，水平偏位时偏位杆所在位置应力集中十分显著，其余传力杆所在位置应力集中水平较低，且受力接近。这是因为水平偏位时其余传力杆的裹附混凝土较平均分摊了偏位导致的应力。

竖向偏位时最大主应力在板接缝处横向分布如图5所示。从图5 可看出，竖向偏位时的应力集中水平相比水平偏位时更高。这是因为竖向偏位时只有临近偏位杆的传力杆分担偏位导致的应力集中（图5 中7 号和9 号杆周围受力明显高于其余未偏位杆）。

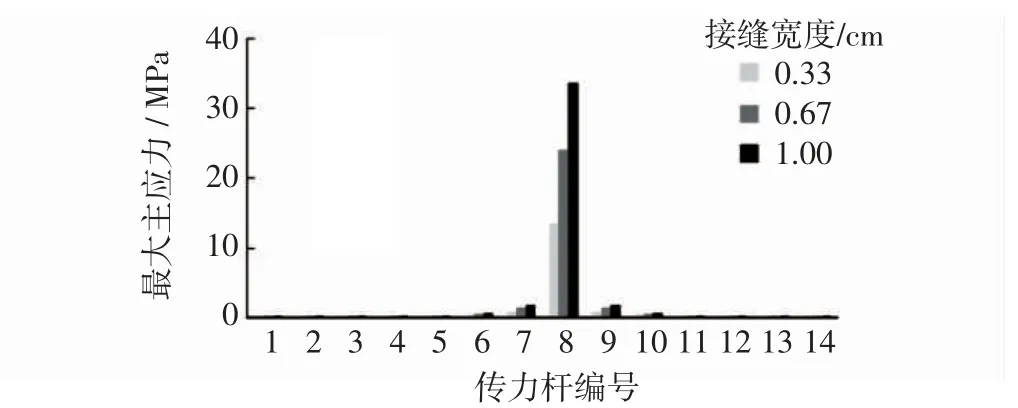
图5 竖向偏位时最大主应力在板接缝处横向分布（偏位角为1.8°）Fig.5 Horizontal distribution of maximum principal stress at joint with vertical deviation angle 1.8°

2.2 两根传力杆偏位的影响

计算两根传力杆水平偏位时包括同向水平偏位和异向水平偏位，如图6 和图7所示。

图6 两根传力杆同向水平偏位时产生的应力集中（偏位角1.8°）Fig.6 Stress concentration caused by two-bar misalignment horizontally in the same direction with attitude angle 1.8°

图7 两根传力杆异向水平偏位时产生的应力集中（偏位角1.8°）Fig.7 Stress concentration caused by two-bar misalignment horizontally in different direction with attitude angle 1.8°

对比图6 和图7 可知，异向水平偏位时的应力整体较高，且异向水平偏位时非偏位杆周围的混凝土应力接近0，说明异向水平偏位导致非偏位杆的应力集中有一定程度的“抵消”。对比水平偏位的各种工况，包括单杆偏位、双杆同向、双杆异向等9 种工况的应力集中情况，如图8所示。

图8 水平偏位不同工况影响Fig.8 Effect of various working conditions on horizontal misalignment

从图8 中可看出：当传力杆偏位量较小时（偏位角1.8°），两根传力杆同向偏位和异向偏位产生的应力集中比单根传力杆偏位时产生的应力集中大；当传力杆偏位量变大时（偏位角3.6°和5.4°），两根传力杆同向偏位和异向偏位产生的应力集中均比单根传力杆偏位产生的应力集中小；不论偏位程度大小，异向偏位比同向偏位产生的应力集中均更大。

计算两根传力杆竖向偏位时同向偏位和异向偏位的影响，如图9所示。

图9 两根传力杆竖向偏位时产生的应力集中（偏位角1.8°）Fig.9 Stress concentration caused by two-bar misalignment vertically in the same direction with attitude angle 1.8°

从图9 中可看出，两者的应力集中的差异没有水平偏位时差异大，这是因为水平偏位中同向或异向偏位对其余传力杆的应力分配有影响，而竖向偏位则不明显。

对比竖向偏位的各种工况，包括单杆偏位、双杆同向、双杆异向几种工况的应力集中情况，如图10所示。

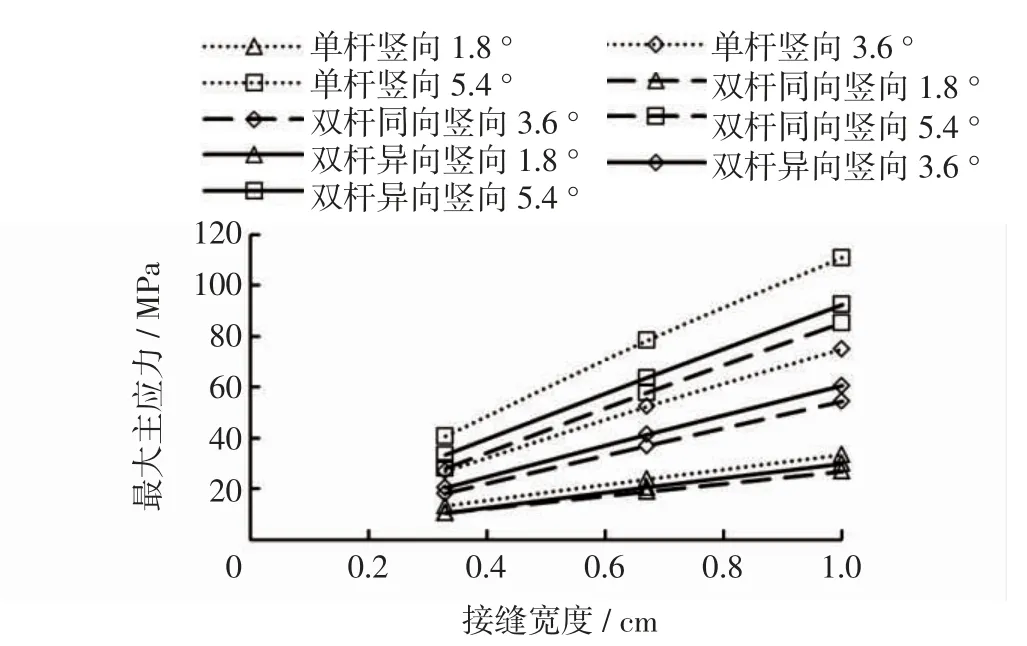
图10 竖向偏位不同工况影响Fig.10 Effect of various working conditions on vertical misalignment

从图10 中可以看出：竖向偏位导致的应力集中也是单杆时最为明显，双杆同向和异向的偏位都使最大主应力降低；异向偏位产生的应力集中高于同向偏位产生的应力集中。

3 飞机荷载作用下传力杆处混凝土应力分析

飞机荷载作用下传力杆处混凝土在各工况下最大主应力值，如图11所示，其中图例命名规则为：无偏位为0°；单杆水平偏位为SH，单杆竖向偏位为SV；双杆水平同向偏位为DHS，双杆水平异向偏位为DHD；双杆竖向同向偏位为DVS，双杆竖向异向偏位为DVD；带（*）的工况表示荷载下传力杆露出混凝土部分朝向荷载作用点方向旋转（工况1），不带（*）的工况表示荷载下传力杆露出混凝土部分背向荷载作用点方向旋转（工况2）。孔口圆周以孔口最底部为0°，逆时针旋转一周为360°，以此设为横坐标。

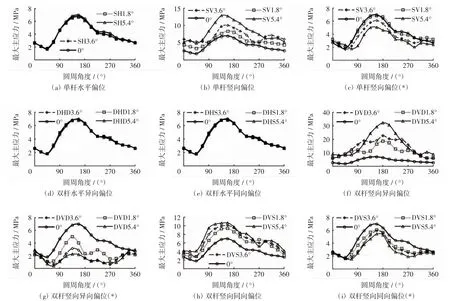
图11 传力杆处混凝土在各工况下的最大主应力值Fig.11 Maximum principal stress of concrete around dowel bars under various conditions

从图11（a）、图11（d）和图11（e）中可以看出，传力杆的水平偏位对裹附混凝土的应力集中影响很小，基本可以忽略。相比而言，竖向偏位对裹附混凝土的应力集中影响十分明显。从图11（b）中可看出，在此工况下最大主应力随着单根传力杆的偏位程度增加而增大，偏位角从1.8°增加到5.4°时，最大主应力增大近一倍。从图11（c）中可看出，在带（*）工况下单杆竖向偏位时，最大主应力随着传力杆的偏位程度增加而减小，偏位角从1.8°增加到5.4°时，最大主应力减小接近1/3。从图11（f）和图11（g）可看出，最大主应力随着传力杆的偏位程度增加而分别增加和减小，但增加和减小的效果都比单杆时更明显，说明双杆异向偏位会使应力水平变化加剧。从图11（h）和图11（i）中可看出，双杆竖向同向偏位使应力变化被削弱，图11（h）中从不偏位到偏位，最大主应力增加不到100%，而图11（f）中最大主应力则增加400%～500%；图11（i）中从不偏位到偏位，最大主应力减小不到25%，而图11（g）中最大主应力降低近70%。

图11 中竖向偏位时包括两种受荷情形（通过是否标记（*）作为区别）。两种受荷情形如图12所示。从图12 可看出，工况1 情况下最大主应力相比工况2更小，工况更为有利。

图12 竖向偏位时两种受荷情形Fig.12 Two different loading conditions with vertical misalignment

4 传力杆偏位影响的试验验证

为验证有限元的计算结果，探究传力杆偏位在实际受荷时的破坏规律，使用材料试验机进行了单根传力杆偏位的子结构加载试验。先成型偏位角均为5.4°时的竖向偏转两种工况及水平偏转试件，其中：混凝土使用C40 强度；传力杆使用普通Q235 圆钢。试件尺寸为20 cm×20 cm×22 cm（沿传力杆长度方向为22 cm），试件尾端固定，在特制材料测试系统（MTS）平台以1 mm/min 速度进行加载。试验结果如图13所示。

图13 传力杆偏位的子结构测试结果Fig.13 Loading test results of sub-structure of dowel bar misalignment

从图13 中可看出，传力杆偏位后水平偏位和竖向偏位表现出不同的受力特征，其中水平偏位和竖向偏位（*）时的支承模量（与斜率相关）基本维持不变，但竖向偏位时的支承模量明显降低，说明传荷系统结构的变化对支承模量的数值有较大影响。此外，竖向偏位时极限承载力降低为正常值的64.1%，说明此结构下的混凝土很快进入塑性屈服且开裂破坏的状态。

此外，在超过极限承载力后，在结构完全解体之前，混凝土对传力杆仍具有一定的承载能力。竖向偏位（*）和无偏位时混凝土能承受的传力杆竖向位移都较大，分别大于2 mm 和大于1.5 mm。有限元分析得到竖向偏位（*）工况最优（最大主应力最小），但由于试验误差，试验结果仅测得竖向偏位（*）工况与无偏位时承载力接近。虽然竖向偏位（*）的工况为最优工况，但由于机轮在从竖向偏位（*）的工况移动到相邻板时，会产生竖向偏位的工况。因此无竖向偏位是最佳选择，机场道面施工中仍应尽可能防止竖向偏位的发生。

5 结语

使用有限元模型分析计算了传力杆发生偏位时，在板温度收缩和飞机荷载分别作用下，传力杆裹附混凝土产生的应力分布和应力集中的规律。通过传力杆偏位子结构的试验，侧面验证了有限元的计算结果，得到了混凝土破坏发生的规律。有以下主要结论。

（1）板温收缩时，随着接缝宽度增大，最大主应力近似线性增长，偏位角度和增长速率有关，偏位越大，最大主应力增长越快。

（2）板温收缩时，水平偏位产生的应力集中普遍比竖向偏位产生的应力集中略低，因为水平偏位时混凝土的应力集中部分平均分配于非偏位的传力杆周围。

（3）板温收缩且双杆偏位时，异向偏位导致非偏位杆的应力集中有一定程度的“抵消”，从而在偏位杆周围的应力集中更明显。

（4）飞机荷载作用下，传力杆的水平偏位对裹附混凝土的应力集中的影响可以忽略，使应力集中降低；传力杆的竖向偏位对裹附混凝土的应力影响十分明显，应力集中提高。

（5）飞机荷载作用下，双杆竖向异向偏位会加剧应力变化，而双杆竖向同向偏位时应力水平则被削弱。

（6）传力杆偏位的极限承载力试验与有限元计算分析的变化规律基本吻合。荷载作用下，虽然竖向偏位两种工况一种有利，一种不利，但由于竖向偏位两种工况相互伴随，因此在施工中机场道面仍需要采取措施保证传力杆不产生竖向偏位。