基于H模型的随钻振动误差建模

杨金显，赵 淳

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

随钻测量MWD(measurement while drilling)是指钻机在钻进时连续不断地检测有关钻孔或钻头的信息[1]。三轴加速度计是MWD核心测量器件，实际工作中不断向控制系统提供井斜信息，并对工具面角的解算提供重要信息。由于加速度计距离钻头很近，其输出信号含大量振动干扰，导致随钻测量结果精度差，因此需要建立随钻非线性振动误差模型并予以补偿。

目前在随钻加速度计振动误差信号处理上，常见方法有以下几种。孙云涛等[2]在井斜动态测量时对重力加速度固有频带外的振动干扰采用低通滤波器处理，实际上振动加速度的频带范围较宽，在固有频带内仍有振动干扰，且对姿态估计实时性有很大影响[3]。徐宝昌等[4]提出在旋转导向钻进中建立钻具振动加速度噪声模型，采用改进UKF滤波去除有色噪声，但该方法主要考虑了钻具轴向振动影响，对于复杂化振动干扰将出现较大的解算误差。王涛等[5]提出了适用于随钻测量振动条件的加速度计36阶Kalman滤波器，测量精度提高，但需要对各项器件误差进行分离、辨识与补偿。Xue等[6]建立一种连续测量数学模型来减少加速度计动态测量误差，在钻头不同运动模式下使用不同信号处理方法。Yang等[7]提出一种借助磁和惯性数据提取钻具重力信息的方法，振动干扰显著时精度不高。

考虑到加速度计振动误差模型的辨识难点在于复杂振动干扰，不确定激励与响应的关系，人为构造模型难以描述过程特征。因此，本文旨在通过黑箱模型估计振动误差，基于改进Hammerstein(以下简称H)模型建立非线性振动函数，利用较少的输入输出辨识数据，实现对加速度计振动误差建模，具有简单、易辨识、计算量少、较好反应过程特征等优点。

1 振动误差建模

1.1 建模方法

钻柱振动受钻井参数、钻具组合、井深结构、钻柱结构等因素影响[8]。钻具振动主要分为纵向振动、横向振动和扭转振动[9]。实际随钻工作中，振动的表现形式更加多样[10]。Lobo等[11]证实由于不确定性和环境因素，用随机模型建立钻柱振动模型。Tian等[12]对钻柱粘滑振动特性建立扭转动力学模型。Mohammadzadeh等[13]研究钻柱的全耦合非线性振动动态模型。钻柱振动的非线性特性复杂，振动冲击对钻柱的全部干扰无从得知，人为构造模型难以描述过程特征，因此选择H黑箱模型分析振动特性。目前，H模型因其特殊结构将非线性控制问题简化为线性模型预测控制问题，广泛应用于非线性系统识别、信号处理和控制工程实践当中[14]，如多传感器系统、电力系统和神经系统等。

井斜测量时，随钻测量系统紧邻钻头安装[15]。MWD加速度计安装于钻杆内，各加速度计的安装轴向如图1所示。

图1 加速度计安装示意图Fig.1 Installation diagram of the accelerometer

随钻系统进行作业时，实际钻进轨迹与设计轨迹会出现偏差，因此传感器数据准确对轨迹修正至关重要。钻进轨迹的倾斜角(倾角、井斜角)指的是井眼轴线的切线与铅垂直线的夹角，完全由加速度解算得到。基于图1三轴加速度计安装坐标系，建立图2随钻钻进图。

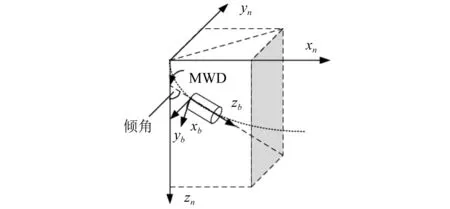
图2 随钻钻进图Fig.2 Diagram of drilling while drilling

钻进过程中，钻具的强烈振动使三轴加速度计的输出包含大量振动干扰，导致姿态解算精度不高。为了从含有大量振动信号的原始信号中得到所需的有用数据，需要对三轴加速度信号进行处理。

钻柱振动信号是典型的非平稳随机信号[16]。加速度传感器受到的振动干扰也是随机信号，显著特点是非周期性和瞬时值不易预测，但其统计特性是有规律的[17]。为能在井底复杂环境下，加速度计仍能得到精确的井斜角，需要对随机振动特性进行误差分析。本文基于H模型，从中间变量不可测的角度，视振动输入为加速度计的一种有色噪声，表示为线性动态模块与非线性静态模块串联的形式，然后分别进行参数辨识[18]。由于H模型辨识参数少，且较好的解决了时变性、非线性问题，提高了辨识精度，该模型如图3所示。

图3 随钻振动的H模型Fig.3 H model of vibration while drilling

其中，加速度计随钻振动H模型由非线性环节、线性环节和随机振动干扰信号组成；非线性部分N(.)以uN真实加速度输入作为输入信号，非线性环节输出N(uN)，表示含非线性误差的有效加速度；线性部分L(.)以N(uN)为输入信号，xN为加速度计受到离心力等影响的动态转动加速度，尚未受到振动干扰，是未知中间变量；ξN为随钻随机振动干扰下输入的有色噪声；yN为加速度计随机振动实际输出。

图3(a)中，需要将待辨识模型中的有色噪声ξN白化为白噪声εN。非线性环节输出N(uN)作为简化模型图3(b)的输入信号，xN为过程模型输出，εN为零均值白噪声，ξN为有色噪声，yN为含噪输出加速度，A(z-1)，B(z-1)，C(z-1)单位后移算子z-1多项式。

从图3可知，H模型输出可表示为

yN=xN+ξN

(1)

(2)

(3)

式中：βi为非线性环节基函数g(.)的系数；r为加速度计噪声模型中非线性环节的阶数。

过程模型

(4)

噪声模型

(5)

式中：A(z-1)=1+a1z-1+a2z-2+…+anaz-na；B(z-1)=b1z-1+b2z-2+…+bnbz-nb；C(z-1)=1+c1z-1+c2z-2+…+cncz-nc。

将式(3)代入式(2)得到

(6)

式中：φN=(-yN-1,…,-yN-Na,g1(uN-1),…,g1(uN-Nb)；g2(uN-1),…,g2(uN-nb),…,gm(uN-nb)；εN-1,…,εN-nc)T；θ=(a1,…,ana,β1b1,…,β1bnb,β2b1,…,β2bnb,…,βrb1,…,βrbnb,c1,…,cnc)T。

图4 加速度计信号处理Fig.4 Accelerometer signal processing

具体算法步骤：

步骤1利用测量数据集进行模型参数辨识，得到非线性结构参数初值c1,…,cnc、线性结构参数初值a1,…,ana以及b1,…,bnb；

步骤2采样当前系统输出，得到最新的误差Δδ；

步骤3通过与条件阈值Δλ比较更新调节系数γ；

步骤4得到最新的H误差模型；

步骤5计算加速度值；

步骤6下一采样点，返回步骤2继续循环。

1.2 参数辨识

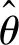
定义参数向量

θ=[θaθβbθc]T

(7)

式中：θa=[a1,a2,…,ana]T；θβb=[β1b1,…,β1bnb,β2b1,…,βrbnb]T；θc=[c1,c2,…,cnc]T；nβb=nβ*nb，na=nb，n=na+nβb+nc。

定义信息向量

(8)

式中，φNs=[-yN-1,…,-yN-na,g1(uN-1),…,g1(uN-nb),…,gr(uN-nb)]T；φNn=[ξN-1,…,ξN-nc]T。

(9)

根据贝叶斯公式，参数的后验概率密度函数为

(10)

(11)

(12)

综上，给定随钻随机振动时的实测输入、输出数据集DN，参数的后验概率密度

(13)

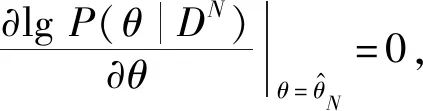
(14)

(15)

(16)

从上式可以得出，当前时刻的噪声方差可近似等于上一时刻的噪声方差

(17)

估计参数向量

(18)

增益矩阵

(19)

协方差矩阵

(20)

(21)

经过适当的矩阵变换，得到βi的表达式

(22)

2 模型修正

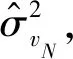
(23)

考虑到实际随钻测量振动环境的强时变性、强非线性，还有随着上述随钻振动模型参数递推辨识算法对时变参数追踪能力的增强，也会造成对噪声愈加敏感，因此提出引入条件阈值Δλ、调节系数γ，将随钻系统的钻头运动状态与调节系数关联起来，对随机振动模型进行修正，提高辨识灵敏度

(24)

(25)

式(25)表征钻头的运动状态与调节系数之间的反比关系。将初始调节参数与钻头运动状态关联起来，可以拓宽调节系数的变化范围，使参数递推辨识过程更细致地跟随钻头的随机振动过程，从而建立更加精确的随机振动误差模型。

(1)Δδ<Δλ，认为当前随钻振动模型已经比较准确，故保持模型不变。

(2)Δλ<Δδ，认为当前随钻振动模型无法准确描述样本信息，需要自适应更新参数。

(26)

式中：初始调节参数γ0与钻头运动状态的关系可以用分段函数表示，δ1，δ2，Δγ1，Δγ2是与钻头运动状态相关的常值。Δδ/Δλ≤1表征钻头位于静止状态，1<Δδ/Δλ≤δ1，表征钻头工作位于低动态，δ1<Δδ/Δλ≤δ2，表征钻头处于高动态，实际随钻工作中钻头的转速通常处于低动态。Δδ为当前时刻系统实际输出值与估计的残差，Δλ为条件阈值，γ0为默认调节系数，算法推导流程如图5。

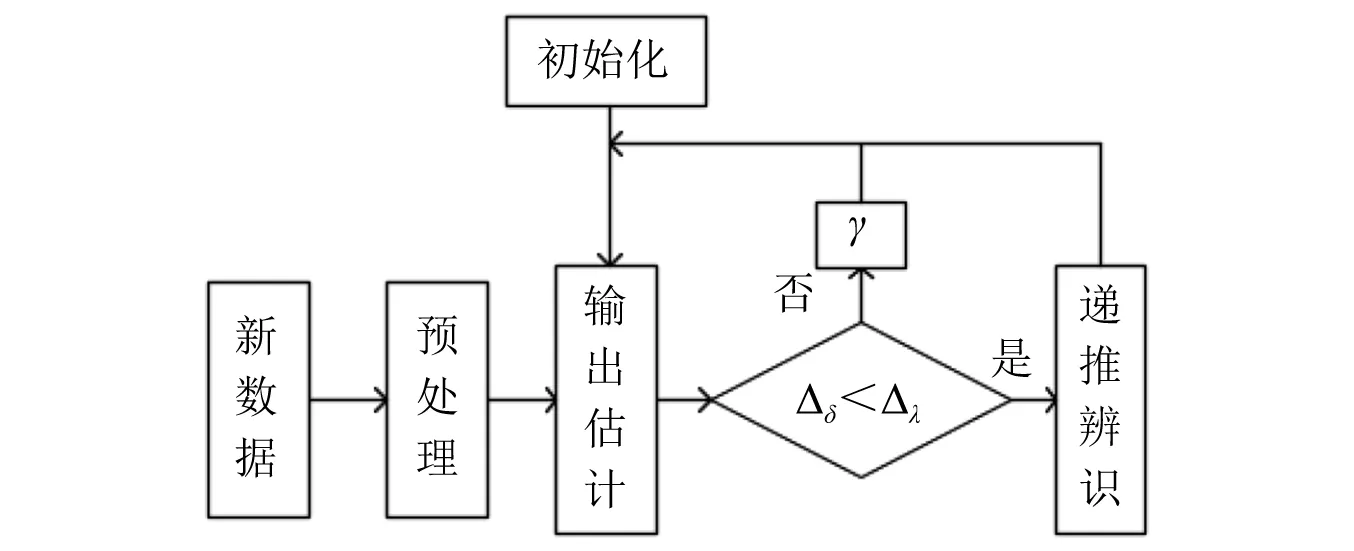
图5 算法流程Fig.5 Algorithm flow

参数向量

(27)

增益矩阵

(28)

协方差矩阵

(29)

3 实验验证及分析

3.1 钻进模拟实验

为验证算法性能，在实验室条件下进行垂直钻进模拟实验。实验场地条件为北纬35°，东经113°，地球自转角速度15°/h，地球重力加速度为9.8 m/s2。实验所需设备有某型工程用小型钻机，MEMS随钻测量模块和模拟地质层等。将随钻测量核心模块(已标定)固定在小型钻机钻杆上，随钻杆一起转动，如图6所示。根据随钻工作时加速度计的随机振动误差特性，选取该模型线性环节和非线性环节阶数分别为r=2，na=nb=nc=3，垂直钻进实验之前，调整钻杆垂直并固定，测量静态初始加速度；钻进实验中，以转速360°/s及恒定钻压进行垂直钻进，以200 Hz采样频率采集加速度数据作为初始数据集，将测量数据集DN按照1.2节分析流程估计模型参数，最后不断采样当前系统输出，更新模型参数；实验结束后，选取其中1 000组数据进行算法处理。

图6 钻进模拟Fig.6 Drilling simulation

由前文分析可知，真实随钻加速度的获取，依赖振动加速度ξ的确定。实际应用中，已知振动误差模型阶数na=3，nc=3，由初始数据集确定初始参数后，不断采样更新模型参数向量θN，分解得到参数{c1,c2,…,cn}，根据噪声模型计算得到当前时刻的振动加速度ξN=C(z-1)/A(z-1)εN，算法处理前后加速度曲线的对比如图7所示。由图可知，随机振动下加速度计的输出误差具有显著波动性和随机性，变化范围始终保持在一定区间内，但趋势项并不明显，所建立的随钻随机振动模型呈现出和原始序列相同趋势，拟合效果较为理想。

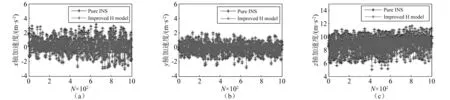
图7 模拟钻进加速度曲线Fig.7 Vibration acceleration curves

为进一步精确验证所得模型的有效性，将随机振动状态下的实际输出与基于非线性模型的预测输出对比，利用标准均方根误差(NRSME)适应度值评价模型预测输出与实测输出的拟合程度，如表1所示。

表1 各轴向数据NRSME适应度值Tab.1 NRSME fitness value of each axial data

(30)

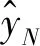
通过NRSME适应度值表可看出基于H模型的自适应算法预测误差较小，拟合程度较高，该模型能较好描述随钻随机振动情况下加速度计的振动动态特性，验证了建模方法的有效性。

3.2 钻进实验

为进一步证明基于H模型的随钻振动误差模型的可行性，选择焦作某煤矿的垂直钻进实验测试数据进行实验验证，部分实钻数据如表2所示，高精度测井仪器测量的实际轨迹曲线和测量轨迹曲线对比如图8所示。考虑随钻加速度计振动误差特性，选取该模型线性环节和非线性环节阶数取值同前，垂直钻进开始时采集少量输入输出数据作为初始数据集，用测量数据集辨识模型参数，并采样系统当前输出，在线更新加速度计的随钻振动误差模型。

表2 部分实钻加速度数据Tab.2 Partially drilled data

图8 钻进轨迹Fig.8 Drilling trajectory

通过前述流程计算相应的振动加速度，对比基于改进H模型的随钻振动误差模型和原始垂直钻进的三轴加速度计输出，产生了如图9所示的加速度拟合曲线。从图中可看出，基于改进H模型得出的预测序列，与原始序列趋势相同，拟合效果较为理想，实钻加速度数据算法处理后的NRSME适应度值表如表3所示。

图9 实钻加速度曲线Fig.9 True drilling acceleration curves

表3 各轴向数据NRSME适应度值Tab.3 NRSME fitness value of each axial data

从表3可直观看出基于改进H模型的自适应算法预测误差较小，拟合程度较高，说明自适应非线性H模型能够较好地描述随钻随机振动情况下加速度计的振动动态特性，验证了建模方法的有效性。

最后，随钻加速度计振动误差建模成功后，对测量数据的处理是否符合实际的轨迹曲线角度，通过计算算法补偿后的井斜角与实际轨迹角度的对比图来说明补偿效果，如图10所示。

图10 实钻井斜角曲线图Fig.10 Actual drilling angle curve

从图8～10可知，基于改进H模型的自适应算法预测误差准确，数据处理后的测量值与实际轨迹曲线较为一致，实验证明自适应非线性H模型能够较好地描述随钻随机振动情况下加速度计的振动动态特性，验证了建模方法的有效性。

4 结 论

目前对随钻测量过程中钻具的实际振动进行测试还是有一定困难的，针对随钻测量时钻具振动使加速度测量信号含大量振动干扰，测量精度不高的问题，提出一种建立非线性随钻振动误差模型的方法来获取真实随钻加速度。本文设计一种改进的基于自适应H模型算法，建立加速度随机振动误差模型，利用递推贝叶斯算法辨识参数，引入条件阈值和调节系数与钻头运动状态关联起来，提高辨识灵敏度，最后设计实验研究MWD真实振动环境下输出加速度的随机振动误差规律，实验结果表明很好地实现对加速度计随机振动误差序列的拟合估计，说明建模方法是有效的，对工程应用中随钻随机振动误差的建模与实时补偿具有重要的参考价值。