一般约束边界下多孔FGM梁的非线性气动热弹性动力学特性研究

周 凯，倪 臻，华宏星

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240)

超声速飞行器在巡航和再入过程中面临着严酷的气动力和热载荷复合环境，对飞行器结构的完整性和可靠性提出了挑战[1]。功能梯度材料(functionally graded material，FGM)因其良好的热力性能，在飞行器结构中得到了广泛的应用[2]。超声速飞行器中存在诸多细长的结构，该类结构具有梁的弹性力学特征，因此可以简化为梁结构[3]。掌握FGM梁结构在气动力和热载荷作用下的动力学特性，是开展结构动态化设计及优化研究的基础。因此，开展FGM梁的非线性气动热弹性动力学研究具有重要的科学价值和工程意义。

现阶段，有较多学者开展了梁的非线性振动问题研究。解析法、有限元法、里茨法和伽辽金等方法广泛地应用于各向同性梁、正交各向异性梁、三明治梁和FGM梁等的非线性振动研究，并取得了一系列的成果[4-6]。近年来，梁结构的气弹动力学问题亦得到了学者们广泛地关注，层合梁、三明治梁和FGM梁的气弹动力学问题得到了充分地研究[7-9]。但值得一提的是，上述梁的气弹动力学研究大多是基于经典约束边界条件下开展的。

近期的研究发现，FGM材料在加工制作过程中，由于材料各组分的凝固温度不同，致使结构中极易产生孔隙[10]。为探究孔隙对梁结构动力学特性的影响，有学者研究了多孔FGM梁的振动问题[11]，结果表明孔隙对于FGM梁的动力学特性具有显著的影响。

由上述文献可知，尽管现阶段有较多关于梁的气动热弹性动力学问题的文献，但目前该方面的研究仍存在以下不足：一方面，现有梁的气动热弹性动力学问题大多是基于经典边界展开的，但由于结构约束在振动环境中存在弹性变形，将边界视为弹性更为合理[12]；另一方面，现阶段关于多孔FGM梁的非线性气动热弹性动力学问题的研究不足，孔隙对于气动力和热载荷作用下FGM梁结构的动力学特性的影响规律不清。因此，亟需开展一般约束边界下多孔FGM梁的非线性气动热弹性动力学研究。

本文将开展一般约束边界下多孔FGM梁的非线性气动热弹性动力学建模与影响机制研究。首先应用一阶剪切变形理论和von-Karman大变形理论，推导梁结构的动能和势能表达式；基于活塞理论和热弹性理论，推导气动力和热载荷的做功表达式；在此基础上应用罚函数法，将边界约束的能量引入系统整体的能量泛函。基于Hamilton原理，推导系统的控制方程并求解，通过数值算例验证理论模型的正确性。最后，通过变参数计算，探讨约束边界、FG材料指数、温度和孔隙率等参数对于FGM梁非线性动力学特性的影响规律。

1 模型描述及公式推导

1.1 模型描述

研究飞行器壁板的气弹动力学问题，一般采用板壳模型或梁模型。对比长宽比接近的壁板结构，其长度和宽度方向变形对系统的气弹特性影响较大，因此多采用板壳模型；对于细长的结构，可以按照梁模型进行分析，同时梁模型为一维结构，其动力学特性分析的计算量将小于板壳模型的计算量[13-16]。因此，细长的结构可以简化为梁模型。本文将研究细长FGM结构的气弹动力学特性，将其简化为梁结构，如图1所示，其长宽高分别为L，b和h，笛卡尔坐标系建立于结构左端几何中面上。

图1 FGM梁示意图Fig.1 The schematic diagram of the heated FGM beam

为了简化建模过程，本文主要假设如下：①超声速气流沿着梁的x轴方向；②温差存在于梁的厚度方向，同一高度截面上梁的温度相同；③基于Timoshenko梁理论考虑梁的变形，梁的两端受支撑约束。为模拟梁的各种边界条件，三组虚拟弹簧ku，kw和kx布置于梁的两端，分别模拟两端支撑的纵向、横向和转动约束。通过修改虚拟弹簧的刚度值，即可等效模拟各种经典边界和弹性边界条件[17]。举例来说，固支梁可将虚拟弹簧的刚度值设为无穷大，而自由梁可将虚拟弹簧的刚度值设为零，弹性约束边界按照实际的约束刚度值给定即可。

考虑到FGM梁在加工过程中极易产生孔隙，而这些孔隙对梁的力学性能具有显著的影响。因此，本文将考虑孔隙的影响。根据文献[10]，FGM材料的孔隙可大致分为两类：当孔隙均匀分布于梁的厚度方向时，此处定义为Ⅰ型均匀多孔梁；当孔隙集中分布于梁的中面时，定义为Ⅱ型非均匀多孔梁。两者示意图如图2所示。

图2 多孔FGM梁示意图Fig.2 The schematic diagram of the porousFGMbeam

1.2 材料特性

假设FGM梁由陶瓷和金属两种材料构成，假定材料的属性沿着梁的厚度方向以指数形式变化，梁的上下表面分别为纯陶瓷和纯金属材料。由FGM材料参数与温度之间关系可得

P=P0(P-1T-1+1+P1T+P2T2+P3T3)

(1)

式中，P0，P-1，P1，P2和P3分别为相应的系数。

Ⅰ型多孔FGM梁和Ⅱ多孔FGM梁的弹性模量E、热膨胀系数α、密度ρ、热传导率κ及泊松比ν可分别表示为

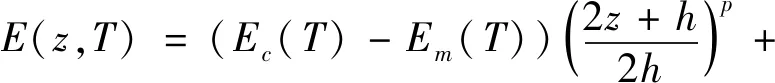
(2)

(3)

式中：下标m和c分别代表金属成分和陶瓷成分；ζ为孔隙率；p为FG材料指数。

假设温差只存在于梁的厚度方向，根据一维傅里叶热传导，可得

(4)

求解式(4)，即可得温度在FGM梁厚度方向的分布。

1.3 控制方程

基于一阶剪切变形理论，多孔FGM梁的位移分量可表示为

(5)

式中：u和w分别为FGM梁中面在x和z方向的位移；φx为转角；t为时间变量。

基于von-Karman大变形理论，多孔FGM梁的应变为

(6)

进一步可得FGM梁的正应力和剪应力

(7)

式中：Ks为剪切修正因子。定义温差ΔT=T-T0，其中T和T0分别为当前温度和参考温度。Q11和Q66分别为FGM梁的弹性系数

(8)

多孔FGM梁的热应力可表示为

(9)

由温度变化引起的热应变为

(10)

基于超声速活塞理论，作用于FGM梁上的气动压力为

(11)

式中，ρ∞，U∞和M∞分别为来流密度、速度及马赫数。

多孔FGM梁的应变能为

(12)

多孔FGM梁的动能为

(13)

储存于FGM梁两端虚拟弹簧中的弹性势能为

(14)

气动力做功为

(15)

因此，系统的整体能量泛函为

Π=Tk-U-UBC+W

(16)

将式(12)～式(15)代入式(16)中，可得由u，w和φx所表示的系统能量泛函的详细表达式。

若直接对式(16)变分，可得系统的偏微分方程组。为离散系统的控制方程，将偏微分方程组转为常微分方程组，本文将利用里茨法求解FGM多孔梁的振动特性[18]。为满足一般约束边界条件，将FGM梁的位移展开为如下的试函数形式[19]

(17)

式中：Am,Bm和Cm为展开系数；试函数具体形式为

(18)

实际数值计算中，式(18)中的无限项试函数应得到截断。假设试函数取至M阶，并将式(12)～式(18)代入Hamilton原理中，令离散后的系统能量泛函对所有展开系数的变分为零，即

(19)

可得离散后的多孔FGM梁的非线性气动热弹性控制方程

(20)

其中，

式中，一般情况下γ=0.5,β=0.25。详细的非线性动力学响应的计算流程如图3所示。

图3 非线性动力学响应的计算流程图Fig.3 The calculation flow chart of the nonlinear dynamic response

2 数值算例

2.1 理论模型验证

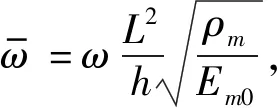
表1 Si3N4/SUS304的材料性能参数Tab.1 The temperature dependent material parameters of Si3N4/SUS304

表2所示为本文模型计算所得的热环境下多孔FGM梁的固有频率与文献[11]中的结果对比。由表2内容的结果可知，本模型计算所得结果与文献结果吻合良好，验证了本方法预测热环境下多孔FGM梁动力学特性的准确性。

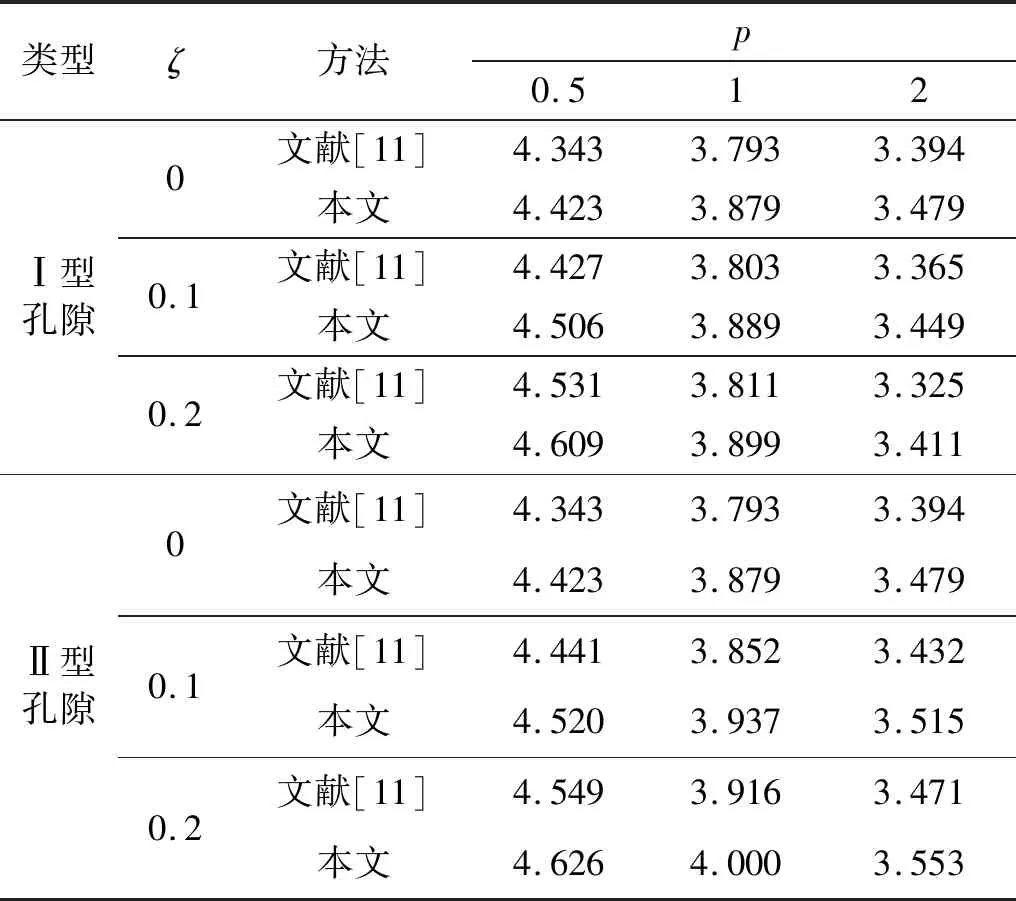
表2 热环境下多孔FGM梁的无量纲固有频率对比Tab.2 The comparisons of non-dimensional natural frequencies of porous FGM beam in the thermal environment

为验证本文模型计算梁结构气弹特性的准确性，进一步将本模型的计算结果与文献[3]中的结果进行对比。此处选取的计算模型参数如表3所示。分别计算S-S和C-F边界下(S：简支；C：固支；F：自由)，梁的固有频率随气动力的变化，并将本文结果与文献[3]中的结果进行对比，如图4所示。由曲线对比可知，本文方法与文献结果吻合良好，验证了本方法的准确性。

表3 梁的尺寸和材料参数Tab.3 The dimensional and material parameters of the beam

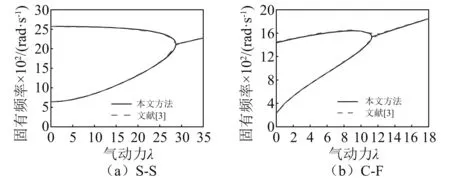
图4 本方法计算所得梁的气弹结果与文献对比Fig.4 The comparisons of the obtained aero-elastic results of beam structures with those from literature

2.2 参数分析

本节开展FGM梁的气弹动力学特性分析，以探讨各参数的影响规律。这里继续选用Si3N4/SUS304梁作为计算模型，梁的尺寸为1.0 m×0.05 m×0.05 m，参考温度T0=300 K。

首先研究气动力对FGM梁动力学特性的影响规律。图5所示为无缺陷简支FGM梁(p=1)在无气动力和临界颤振动压下的前四阶振型对比。经计算，本例FGM梁的临界颤振动压为。显而易见，当无气动力时，FGM梁的一阶振型最大位移点位于0.5L点处；当气动力等于临界颤振动压时，FGM梁的一阶振型最大位移点位于0.75L点处。同时，一旦发生颤振，梁的前两阶模态将发生耦合。

图5 无气动力和临界颤振动压下梁的前四阶振型Fig.5 The first four mode shapes of the FGM beam without aerodynamic pressure and at flutter boundary

同时，计算不同气动力作用下FGM梁在脉冲激励下0.75L点处的动力学响应，分别如图6～图8所示。如图6所示，当λ=0时，由于未考虑梁的结构阻尼，当气动力为零时，FGM梁在受到脉冲激励后作不衰减的周期运动；如图7所示，当气动力不为零且小于临界颤振动压时，由于气动阻尼存在，FGM梁在受到脉冲激励后作衰减运动；如图8所示，当气动力大于等于临界颤振动压时，FGM梁在受到脉冲激励后将作等幅极限环运动。

图6 脉冲激励下梁的动力学响应(λ=1,p=1)Fig.6 The dynamic response of the FGM beam with pulse excitation (λ=1,p=1)

图7 脉冲激励下梁的动力学响应(λ=20,p=1)Fig.7 The dynamic response of the FGM beam with pulse excitation (λ=20,p=1)

图8 脉冲激励下梁的动力学响应(λ=36,p=1)Fig.8 The dynamic response of the FGM beam with pulse excitation (λ=36,p=1)

图9所示为不同约束边界下，无缺陷FGM梁(p=1)的固有频率和0.75L点处的极限环振幅随气动力的变化曲线。这里选取了S-S、S-C和C-C三种边界约束条件。显而易见，由于C-C梁的边界刚度最大，所以它在三者中的临界颤振动压最大，且极限环振幅最小。相反，S-S梁的边界刚度最小，故其临界颤振动压最小，且极限环振幅最大。

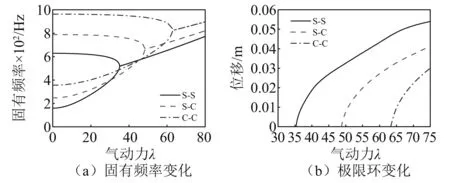
图9 边界对无缺陷FGM梁的固有频率和极限环振幅的影响(p=1)Fig.9 The effect of boundary conditions on the natural frequencies and LCO amplitude of the perfect FGM beam (p=1)

图10所示为不同FG材料指数下，无缺陷简支FGM梁的固有频率和0.75L点处的极限环振幅随气动力的变化曲线。由图中结果可知，随着FG材料指数的增加，梁的临界颤振动压减小，极限环振幅增大。这是由于随着FG材料指数的增加，结构的整体刚度下降所导致的。

图10 FG材料指数对无缺陷FGM梁的固有频率和极限环振幅的影响Fig.10 The effect of the volume fraction index on the natural frequencies and LCO amplitude of simply supported perfect FGM beam

图11所示为不同热环境下，无缺陷简支FGM梁(p=1)的固有频率和0.75L点处的极限环振幅随气动力的变化曲线。假设FGM梁的内层为参考温度T0，而外层温度分别为300 K、450 K和600 K三种不同的工况。可以看出，随着外层温度的增加，FGM梁的临界颤振动压随之下降，极限环振幅增大。这是由于梁内热应力随温度的升高而增大，从而导致结构的整体刚度下降造成的。

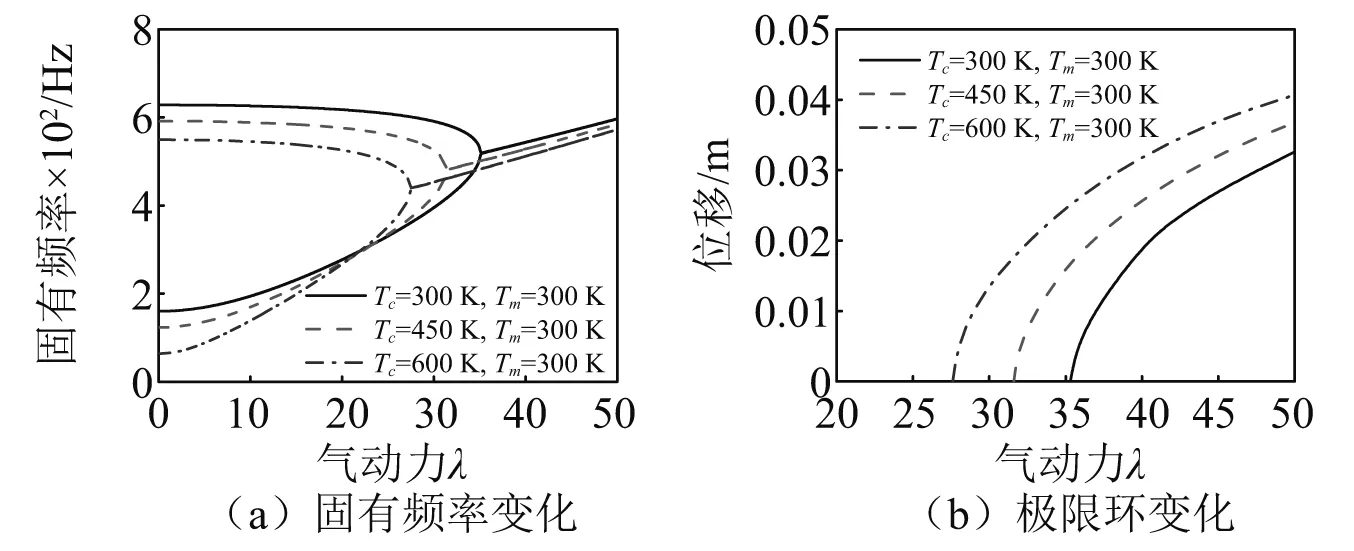
图11 温度对无缺陷简支FGM梁的固有频率和极限环振幅的影响(p=1)Fig.11 The effect of the thermal gradient on the natural frequencies and LCO amplitude of the simply supported perfect FGM beam (p=1)

图12和图13所示为不同孔隙率下，简支FGM梁(p=1)的固有频率和0.75L点处的极限环振幅随气动力的变化曲线。总体而言，随着孔隙率的增加，梁的临界颤振动压减小，极限环振幅增大。但是Ⅰ型孔隙对FGM梁气弹特性的影响大于Ⅱ型，主要由于Ⅰ型孔隙均匀分布在厚度方向上，而Ⅱ型主要集中于中面附近，使得I型孔隙对于结构的整体刚度影响更大。

图12 孔隙率对简支FGM梁的固有频率和极限环振幅的影响(Ⅰ型，p=1)Fig.12 The effect of the porosity volume fraction on the natural frequencies and LCO amplitude of the simply supported FGM beam (Type Ⅰ,p=1)

图13 孔隙率对简支FGM梁的固有频率和极限环振幅的影响(Ⅱ型，p=1)Fig.13 The effect of the porosity volume fraction on the natural frequencies and LCO amplitude of the simply supported FGM beam (Type Ⅱ,p=1)

3 结 论

本文基于能量法，建立了适用于一般约束边界下多孔FGM梁的非线性气动热弹性动力学模型，通过数值算例验证了理论模型的正确性并开展了其动力学特性分析，主要研究结论如下：

(1)本文模型求解的梁的固有频率和临界颤振动压与文献结果基本吻合，验证了本文方法的有效性。

(2)随着边界约束刚度的下降、FG材料指数的增加或热载荷的增大，FGM梁的整体刚度下降，致使结构的临界颤振动压降低、颤振极限环振幅增大。

(3)随着孔隙率的增大，FGM梁的临界颤振动压降低、颤振极限环振幅增大。由于I型孔隙对结构刚度的影响更为显著，致使I型孔隙对FGM梁的气弹特性的影响大于II型孔隙。

附录A

梁的位移可展开为离散形式

u(x,t)=Hqu,w(x,t)=Hqw,φx(x,t)=Hqx

其中，

H=[ψ1(x),ψ2(x),…,ψM(x)]

qu=[A1,A2,…,AM]T，qw=[B1,B2,…,BM]T,

qx=[C1,C2,…,CM]T，Q=[qu;qw;qx]

因此，经离散后梁的结构线性刚度矩阵、结构非线性刚度矩阵、热应力矩阵和气动力矩阵分别为

kux0(H)T(H)|x=0+kuxL(H)T(H)|x=L,

kwx0(H)T(H)|x=0+kwxL(H)T(H)|x=L,

kxx0(H)T(H)|x=0+kxxL(H)T(H)|x=L,

梁的气动阻尼矩阵和质量矩阵分别为