递推关系an+1=qan+p在概率中的应用举例

江苏 郭建华

数列中连续两项的递推关系an+1=qan+p(其中p，q为常数，pq≠0，q≠1)是一种常用的数学模型．该模型在概率中也有着其独特的用法，常常以选择题的形式出现，其综合性强，求解难度较大，重点考查化归与转化，分类讨论等数学思想．对于选择题，可以从选项的描述中获取解题思路，也可以先从特殊化入手，再研究其一般情况，即先猜后证(利用数学归纳法证明)，最后结合求数列的通项公式的手段和方法求解．

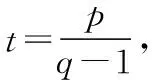
下面，通过两道多项选择题谈谈an+1=qan+p在概率中的应用.

1.摸球问题

【例1】甲口袋中装有2个黑球和1个白球，乙口袋中装有3个白球．现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复n(n∈N*)次这样的操作，记甲口袋中黑球个数为Xn，恰有2个黑球的概率为pn，恰有1个黑球的概率为qn，则下列结论正确的是

( )

B．数列{2pn+qn-1}是等比数列

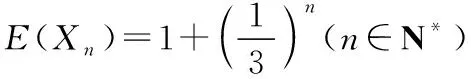
【解析】重复n次这样的操作，记甲口袋的黑球个数为Xn，其取值为0，1，2，恰有2个黑球的概率为pn，恰有1个黑球的概率为qn，此时，甲口袋的球为以下三种情况之一，即2个黑球和1个白球，1个黑球和2个白球，3个白球和0个黑球，所对应的概率分别为pn，qn，1-pn-qn．

从甲、乙两口袋中各任取一个球交换放入另一口袋为一次操作．

(1)若重复(n+1)次这样的操作，甲口袋中黑球个数Xn+1恰好为2，即甲口袋装有2个黑球和1个白球，则重复n次这样的操作时，甲口袋中黑球的个数Xn为1或2，包含以下两个互斥事件，即

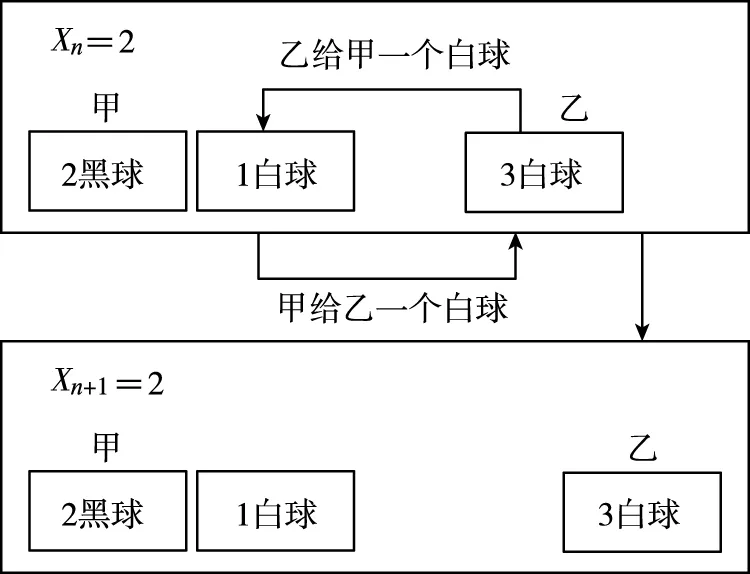
①当Xn=2时，此时，甲口袋装有2个黑球和1个白球，乙口袋装有3个白球，进行一次操作(甲给乙一个白球，同时乙给甲一个白球)后Xn+1=2，于是甲口袋装有2个黑球和1个白球，乙口袋装有3个白球，其交换过程如图所示：

②当Xn=1时，此时，甲口袋装有1个黑球和2个白球，乙口袋装有1个黑球和2个白球，进行一次操作(甲给乙一个白球，同时乙给甲一个黑球)后Xn+1=2，其交换过程如图所示：

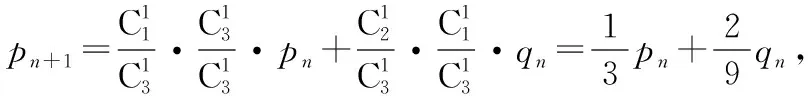
(2)若重复(n+1)次这样的操作，甲口袋中黑球个数Xn+1恰好为1，此时，甲口袋装有1个黑球和2个白球，则重复n次这样的操作时，甲口袋中黑球的个数Xn为0，1或2，包含以下三个互斥事件，即

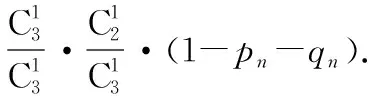
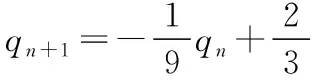
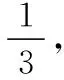
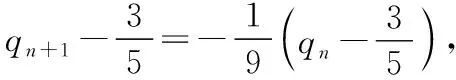
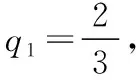
Xn的概率分布为

4月17日，青海省水利厅抗震救灾指挥部迅速部署启动了玉树地震水利工程灾后重建规划编制工作，要求重建规划于5月1日前编制完成。

Xn012P1-pn-qnqnpn

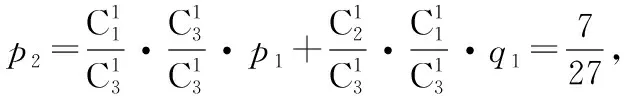
【评注】四个选项的形式多样，考查了概率和数列的重要知识点，达到了交汇考查的目的.从选项中可以猜想pn与qn之间存在一定的联系．如何厘清它们之间的关联，就要分析从第(n-1)次操作到第n次操作会产生怎样的变化．为了将抽象的问题具体化，更易于学生理解，把从第(n-1)次的操作到第n次的操作过程采取思维导图的形式呈现，即采取先一般化再研究特殊化的问题探究方式．也可以从特殊化入手，寻找概率变化的规律，进而猜想pn与qn的一般化形式，再结合概率的知识求解．另外，学生还要熟练掌握具有递推关系an+1=qan+p(其中p，q为常数，pq≠0，q≠1)的数列的通项的求法，再结合数列的知识求解．

2.爬行问题

【例2】设一个正三棱柱ABC-A1B1C1，如图，每条棱长都相等，一只蚂蚁从上底面ABC的某顶点出发，每次只沿着棱爬行并爬到另一个顶点，算一次爬行.若它选择三个方向爬行的概率相等，当蚂蚁爬行n次，仍然在上底面的概率记为Pn，则下列选项正确的是

( )

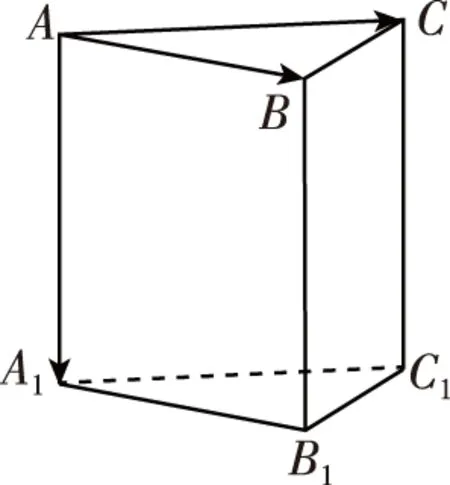
【解析】若蚂蚁爬行n次时，仍然在上底面的概率记为Pn，则蚂蚁爬行(n-1)次时，仍然在上底面的概率记为Pn-1．Pn的大小决定于以下两个互斥事件，即

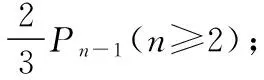
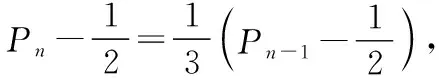
故选项A，C正确，选项B错误．

对于D选项，用数学归纳法证明如下：

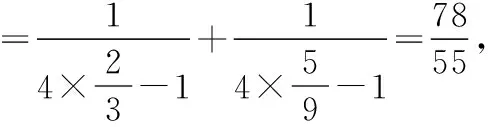
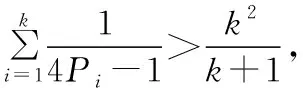
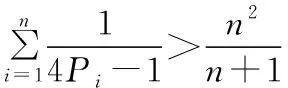
故选ACD．

3.总结