2021年全国乙卷理科第19题的解法探究及思考

新疆 符强如

发展学生数学思维素养，促使知识向核心素养转化，成为中学数学一线教师教学发展方向.数学概念的教学是教学核心之一，深度的数学概念教学有助于发展学生深度思维，笔者通过对2021年全国高考乙卷理科数列题调查后发现，看似简单的一个题目学生反映出的情况却不容乐观，深究问题所在：学生对于数学概念理解处于浅层次.下面通过对这道数列问题进行多角度思考解析，提出概念教学的见解，以期有抛砖引玉之效.

一、题目呈现

(1)证明：数列{bn}是等差数列；

(2)求{an}的通项公式.

【背景】这道题是2021年高考全国乙卷理科第19题，从问题表述来看，此题取材平实, 表现朴实, 题干清晰，传承了全国卷高考命题简约、稳健的风格.从内容上来看，考查等差数列的概念、性质与通项.考查了学生的逻辑推理、数学建模、数学运算等核心素养，要求学生具备突破常规的思维能力，与学生沟通探讨中发现，这道题的得分不容乐观，笔者对此题第一问进行了深入研究, 细致品析, 初尝平淡, 深酌而显深厚蕴藉, 余味绵长.

二、多个视角探究

思路一：“消元”角度，消去Sn

解法1：当n=1时，b1=S1，

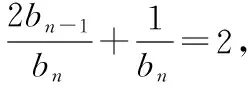
评析：学生需要充分利用bn=S1·S2·…·Sn这一条件,调查发现，学生在常规等差、等比数列的题型中思维难以突破.但对bn=S1·S2·…·Sn条件的理解非常丰富.

比如：(1)直接应用：

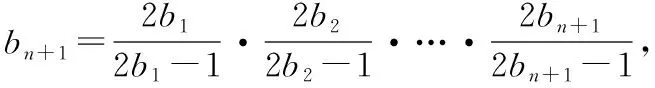
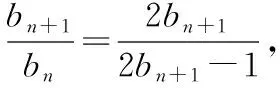
(2)变形bn=bn-1·Sn(n≥2)形式.

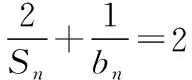
思路二：开门见山应用等差数列定义式bn-bn-1=d(常数)

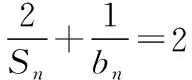
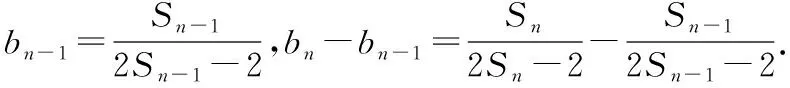
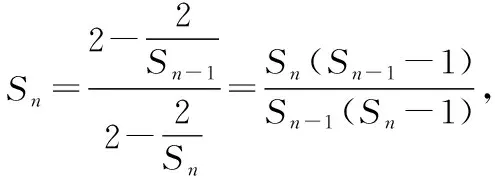
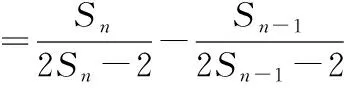
所以数列{bn}是等差数列．

评析：对于解法2是学生经过新知识学习和一定量习题训练后最容易想到的思路.但是发现写出bn-bn-1后与平时训练出现的结果不一样，不少学生就停留在这一步.我们其实往前走一步只需要找到Sn与Sn-1的关系即可，这启示教师在平时教学中应注重学生对非常规题型的处理策略的培养，其问题的本质就是学生对概念理解不到位.那么非常规题型出现学生就会有丰富的处理方案,下面展示不同解法.

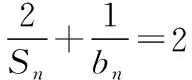
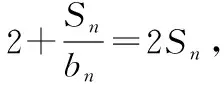
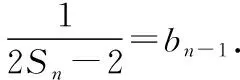
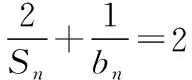
所以数列{bn}是等差数列．

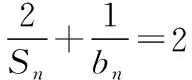
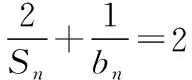
思路三：通过等差中项2bn-1=bn+bn-2(n≥3)求证

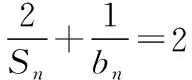
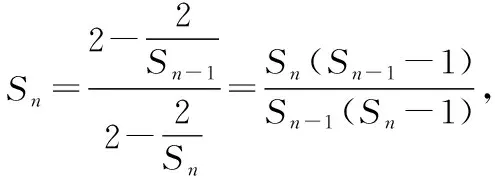
所以2Sn-1=Sn-1·Sn+1,

2bn-1=bn+bn-2(n≥3).

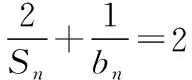
2bn-2bn-1=2bn-1-2bn-2(n≥3)，

即bn+bn-2=2bn-1(n≥3).

评析：思路三也是在探究思路二过程中演变而来的，就是对主干条件变形过程中通过等差中项2bn=bn-1+bn+1(n≥2)来证明，学生直接从等差中项去证明是比较困难的，但是数列的概念反应的特征就是数列，学生就可以通过数学归纳法去求解，也可以先求出Sn，再求bn.

思路四：先求出Sn，再求bn

bn=Sn·bn-1,

三、教学启示

我们一线教学老师发现：当前许多课堂被应试教学主导，数学教学严重异化为解题的模仿与训练，大部分时间培养的只是学生进行机械运算和演绎推理的能力，很难全面且有深度地培育学生的数学思维及核心素养．已严重异化为解题模仿与训练的数学课堂，不能真正激发学生的学习兴趣，学生对数学概念产生的必要性和合理性的感悟严重缺乏，很难直接产生学习新概念的情感需求和思维需求，这种急功近利的做法只能让学生获得碎片、零散的知识记忆和僵化的思维，数学概念的学习停留在机械表层,难以让学生构筑厚实的学习基础，形成必要的探究发现能力，学生的数学思维素养得不到有效地培养．

在平常的数学教学中，概念教学是培育学生数学抽象素养的主要路径.数学抽象是人脑舍去某一类事物所有具体属性得到其相同数学属性的一种思维过程，通常可用数学符号或术语对抽象所得的共同数学属性进行概括和表达．数学抽象主要包括从数量与图形，以及数量关系和图形关系中抽象出数学概念及概念间的关系，以及从事物具体背景抽象出一般规律和结构等过程.在这个过程中，数学认识由感性上升到理性．数学概念教学首先需要研究“为什么学习此概念”，激活学习新概念的情感需求和认知需求；其次需要研究“学习数学概念的哪些内容”，挖掘数学概念的本质及生成过程等.所以在概念教学中，学生数学抽象素养的形成，是基于其对诸多知识和概念相关联知识的整体理解与认识，需要教师适当腾出时间对引入概念的必要性和历史背景等作较详细说明.获得数学概念的主要思维方式是抽象与概括，而抽象与概括是一种思维的体验和领悟.因而，在数学概念教学中，应尽量多地让学生亲历概念的抽象与概括思维过程，在不断地体验与领悟中将经验与概念、直觉与逻辑整体融合并凝聚、升华形成素养.最重要的是要遵循知识的发生发展过程和学生头脑中与新知识有实质性联系的适当观念，以学生认知结构中与新概念有自然的、内在联系的已有知识作为新概念的生长点，使新旧概念之间产生非人为和实质性联系.

数学概念的学习需要数学建模素养，其从数学视角看问题、用数学方法处理问题的意识与能力，是学以致用精神的体现；也是在研究一个现实问题时，先从问题信息抽象出形式化的数学模型，再根据模型求解结果统一处理同类现实问题的思维过程．其以描述客观事物的数形特征和内在联系，所建立的模型和众多的数学概念、公式和定理等知识一样，都可以广泛应用于现实世界．

在概念的应用教学中，教师引导学生整体理解数学知识结构及其思想方法，让学生了解问题的现实意义，以及问题蕴含的数形特征，启发学生用数学符号语言将现实问题转化为数学问题，通过联想将问题选取适当的且已学知识模型.这需要教师多引导学生从数学角度观察、发现并提出有意义的问题，这其中往往会与已学的数学概念、知识和思想方法有广泛联系，能让学生更深刻地理解概念内涵、意义及作用.