2021年新高考Ⅰ卷第19题的多解探究与思考
2021-11-09广东蔡芝芝
广东 蔡芝芝
一、试题呈现
(2021·新高考Ⅰ卷·19)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BDsin∠ABC=asinC.
(1)证明:BD=b;
(2)若AD=2DC,求cos∠ABC.
二、试题分析
本题是解三角形的解答题,题目题干简洁,结构清晰,知识点方面主要考查正弦定理、余弦定理在解三角形问题中的应用,考查的数学思想方法有化归与转化思想、函数与方程思想、数形结合思想、分类讨论思想,涉及的数学核心素养有数学运算、逻辑推理等.本题在学生的学习痛点处设置障碍,强化任务的梯度设计,突出对理性思维的考查是本题的主要特点,体现出基础性,综合性.试题难度方面比往年全国卷Ⅰ的解三角形试题略难一些,考查的载体和考查方式比较新颖,很多考生很不适应,答题情况很不理想.
本题的解答主要有以下三个障碍,一是题中的三角形是不确定的,没有具体的边长数值,需要通过这样一个三角形载体研究其边角关系;二是题目涉及的变量多,题中有三个三角形,每个三角形有六个基本量,可供考生选择的变量较多;三是构建方程的方法多,求解难度大,解三角形问题的核心就是方程的构建和方程的求解,很多考生无法正确构建方程组进行求解,第二问的解题过程中涉及数字及多符号的混合运算,过程比较复杂,没有扎实的运算能力,很难求得正确结果.
三、解法分析
第(1)问的证明过程:
方法一:利用正弦定理边角互化
△ABC中,由正弦定理得c=2RsinC,b=2Rsin∠ABC,
其中2R为△ABC的外接圆直径.
代入BDsin∠ABC=asinC化简得BD×b=ac,
又因为b2=ac,所以BD×b=b2,所以BD=b.
【评注】正弦定理可以实现边与角互相转化,是解决本问题的常规方法,也可以把边化角再进行化简.在答题过程中应该体现正弦定理的应用过程,做到逻辑清晰,表达规范,避免不必要的丢分.
方法二:作高法
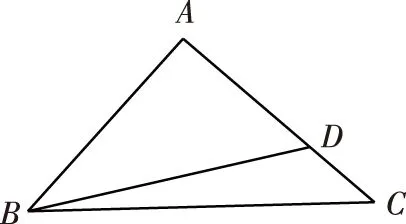
如图所示,过点A作AH⊥BC于H,记AH=h,
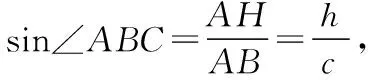
代入BDsin∠ABC=asinC,
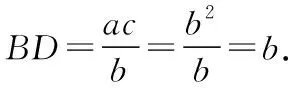

方法三:面积法

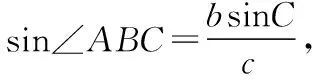
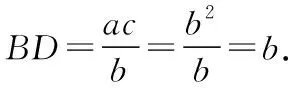
【评注】通过作高或三角形的面积边角互化也是一种常见方法,此两种方法均可用于证明正弦定理,实质上与方法一异曲同工.
方法四:相似三角形法
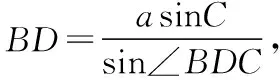
代入BDsin∠ABC=asinC化简得sin∠ABC=sin∠BDC,
若∠ABC=∠BDC,则△BDC∽△ABC,
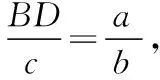
若∠ABC=π-∠BDC,即∠ABC=∠BDA,
则△ADB∽△ABC,
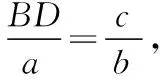
综上所述,BD=b.
【评注】通过已知条件得到∠ABC与∠BDC的关系是此解法的关键,也是本题条件中所蕴含的几何关系,再借助相似三角形的几何关系证明.
第(2)问解答过程:
视角一:余弦定理视角
方法一:构建边的方程法
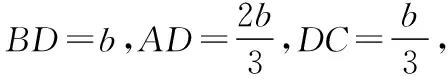

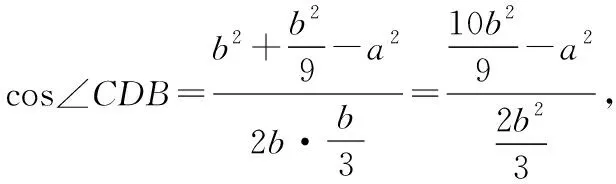
因为∠ADB=π-∠CDB,

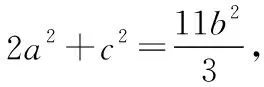
故6a2+3c2-11ac=0,
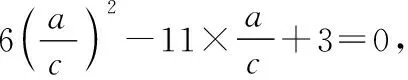
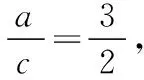
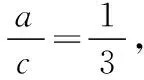
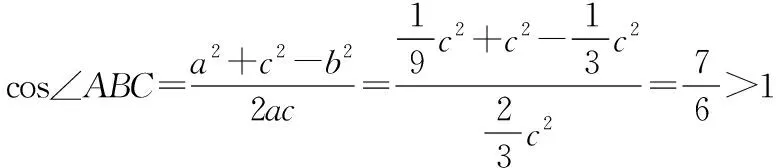
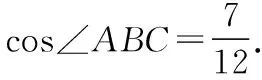
方法二:构建角的方程法
在△ABD中,由余弦定理得
在△BCD中,由余弦定理得
在△ABC中,由余弦定理得
b2=a2+c2-2accos∠ABC,

由第(1)问得sin∠ABC=sin∠BDC,
若cos∠ABC=cos∠BDC,
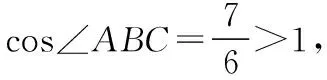
若cos∠ABC=-cos∠BDC,
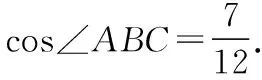
【评注】此题中的三角形共有三个,对于这种多三角形的解三角形问题往往通过相关联的角或边进行构建方程组,体现了函数与方程的数学思想方法在解题中的应用.由∠ADB与∠BDC的互补关系得到a,b,c的数量关系是关键,也是解此类问题的通法通性,此处可以通过两个三角形的公共角A或C的余弦定理来构建方程组进行求解.方法二与方法一在构建方程的方法上是一致的,但是在解方程的过程中消元直接得到目标角的方程,使得求解过程更简洁.
视角二:平面几何视角
方法三:补形法
如图所示,过点C作CE∥AB交BD延长线于E,
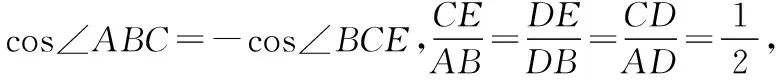
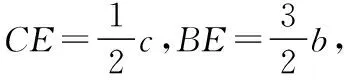
(以下同方法一)

方法四:相似三角形法
由第(1)问得sin∠ABC=sin∠BDC,
若∠ABC=∠BDC,则△BDC∽△ABC,
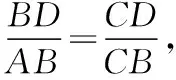
若∠ABC=π-∠BDC,即∠ABC=∠BDA,

(以下同方法一)
【评注】解三角形问题也是一个平面几何问题,通过挖掘图形中的几何关系,把几何关系转化成代数关系再进行求解,体现了数形结合思想方法在解题中的应用.方法三也可以用过A作BC的平行线的方法进行补形.
视角三:平面向量视角
方法五:向量法
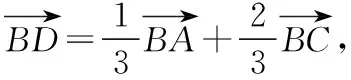
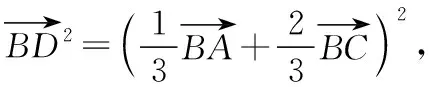
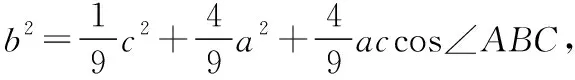

代入上式化简得6a2+3c2-11b2=0.
(以下同方法一)
【评注】向量在高中数学中往往以工具的形态出现,在解决平面几何中的很多问题都有着明显的优势,把几何关系转化成向量关系,再借助向量的运算进行求解是常用的方法.此解法体现了向量的工具属性及化归与转化思想在解题中的应用.
视角四:解析几何视角
方法六:坐标法
以B为坐标原点,BC边所在直线为x轴建立如图所示直角坐标系,
设∠ABC=θ,则B(0,0),A(ccosθ,csinθ),C(a,0),
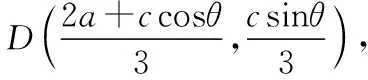
因为BD=b,

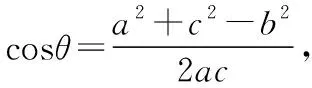
代入上式化简得6a2+3c2-11b2=0.
(以下同方法一)
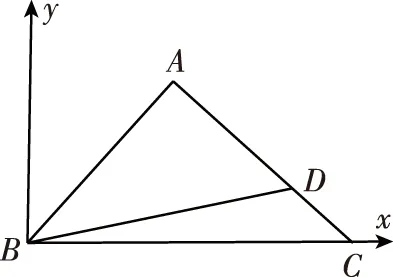
【评注】解析法在解决平面几何的问题中应用广泛,解题的关键在于坐标化,体现了化归与转化思想和数形结合思想的应用.
视角五:经典几何原理视角
方法七:斯特瓦特定理法
因为AD=2DC,所以由斯特瓦特定理知

即化简得6a2+3c2-11b2=0.
(以下同方法一)
方法八:阿波罗尼斯定理法
如图所示,取AD中点E,则D为CE的中点.
设BE=t,则由阿波罗尼斯定理得

消去t并化简得6a2+3c2-11b2=0,
(以下同方法一).

【评注】三角形中的中线长公式、斯特瓦特定理、阿波罗尼斯定理、斯库顿定理等经典的平面几何定理在数学竞赛问题中经常涉及,这些定理对解决三角形中的特殊线段的长度问题有着明显的优势,这些解法的应用让这一道题的背景更加丰富,几何味更浓.
四、解后反思

