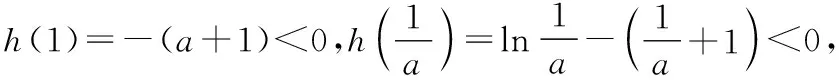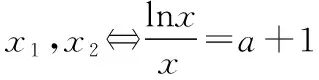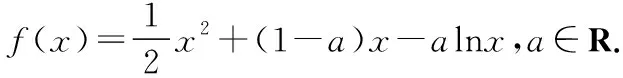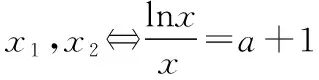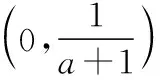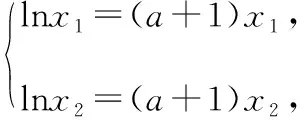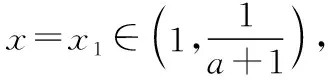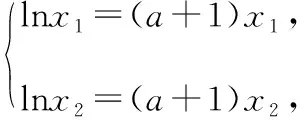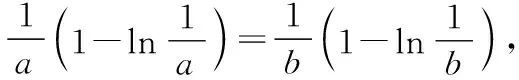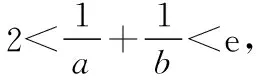导数中含参问题的处理与极值点偏移问题

云南 马孟华

笔者通过对一道高考导数试题的综合分析，提出利用导数解决含参数问题的两种策略，同时利用一题多解的形式对目前最为热门的极值点偏移问题的解法进行深入的探讨和总结，并结合2021年高考试题中的极值点偏移问题进行例证.

1.参数取值范围处理策略

(1)当a=1时，判断函数y=f(x)的单调性；

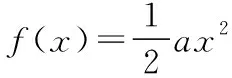
解：(1)解析略，具体看(2).

1.1 数形结合法

方法一:由题意可知lnx=(a+1)x有两个不同的实根x1,x2，

设直线y=kx与y=lnx相切，切点坐标为(x0,y0)，

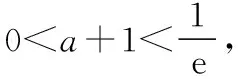
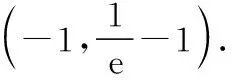
事实上，此问有最为实用的三种解法：

(1)数形结合法；(2)带参讨论法；(3)参变分离法.

上述方法属于数形结合法，将问题转化为切线问题求解，下面再利用“带参讨论法”和“参变分离法”解决实数a的取值范围.

1.2 带参讨论法

方法二:令h(x)=lnx-(a+1)x(x>0).

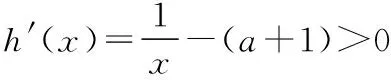
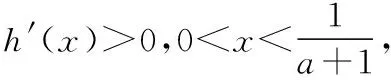
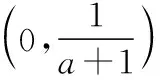
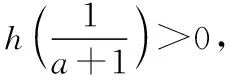
故ln(a+1)<-1，得0

综上,-1

1.3 参变分离法

故当0

【评析】以上三种方法是求解参数取值范围问题的主要方法，在一线教学实践中，“参变分离”“数形结合”是比较符合学生认知规律的思想方法，且容易被学生所掌握和理解.而“带参讨论”的方式由于对思维水平要求较高，且操作过程中具有“复杂性(往往需要分类讨论)”和“特殊性(技巧性较强)”的特点，导致难以实施，学生难以理解和掌握，故在一线教学中可适当加强对前两种方法的思考和尝试.

2.极值点偏移处理策略

结合1.2，1.3可以看到，要证明的不等式属于明显的极值点偏移问题，下面结合教学实践，给出极值点偏移的几种处理方法，并将2021年数学新高考Ⅰ卷中的压轴题也一并进行对比分析整理.下面证明不等式x1x2>e2.

2.1 比值换元法(一)

方法一:由1.1知lnx=(a+1)x有两个不同的实根x1,x2，

故有lnx1=(a+1)x1,lnx2=(a+1)x2,

两式相加得ln(x1x2)=(a+1)(x1+x2)，

要证x1x2>e2，

对于x1,x2，不妨设x2>x1>0,

所以x1x2>e2．

2.2 比值换元法(二)

方法二:由1.3知1

由lnx1=(a+1)x1，lnx2=(a+1)x2,

即x2lnx1=x1lnx2，将x2=tx1代入可得

tx1lnx1=x1lntx1，

即tlnx1=lnt+lnx1,

要证：x1x2>e2，即证

令h(t)=(1+t)lnt-2(t-1)(t>1),

故h′(t)在t∈(1,+∞)上单调递增，从而h′(t)>h′(1)=0,

所以h(t)在t∈(1,+∞)上单调递增，故h(t)>h(1)=0，

即(1+t)lnt-2(t-1)>0在t∈(1,+∞)上恒成立,

所以x1x2>e2．

【评析】此法也比较简洁、快捷，但问题稍微复杂就可能失效，如下题：

此题函数较例题更为复杂，如果进行比值换元后，是无法顺利解出双变量x1,x2的值(即用变量t表示出变量x1,x2)，故此法的最大局限就在于此.注意到比值换元法的缺陷，我们可以考虑解决极值点偏移问题的另一方法，即“对数平均不等式法”，这也是解决此类问题的本质.

2.3 对数平均不等式法

方法三:由2.1知，

故lnx1+lnx2>2,

即有x1x2>e2.

【评析】此法中采用的对数平均不等式，其关键步骤在于能否将结论中所证不等式用对数平均数简洁的表达出来.若能，则问题变得简单，若不能，则对数平均不等式法也就失效了，这也是对数平均不等式法的一个局限.需要注意的是,对数平均不等式的证明也使用了“齐次化换元”的方法，此过程省略了证明过程,直接使用求解.

2.4 函数的选取与构造(一)

当x∈(e,+∞)时，F′(x)>0，故F(x)在(e,+∞)上单调递增，

所以F(x)>F(e)=0,

又g(x1)=g(x2)=a+1，

2.5 函数的选取与构造(二)

方法五：由1.3知方程lnx=(a+1)x有两个不同实根x1，x2，

则函数g(x)=lnx-(a+1)x有两个不同的零点x1,x2,

要证x1x2>e2，即证lnx1+lnx2>2,

令t=lnx∈R，

则lnx1+lnx2>2⟺t1+t2>2，

故要证lnx1+lnx2>2，即证t1+t2>2,

而t1,t2即为函数h(t)=t-(a+1)et(t∈R)的两个零点,

因为当t=0时，m(t)=0,所以直线y=a+1与曲线m(t)交于两点，其横坐标为t1,t2，则0

当t∈(0,1)时，Q′(t)>0，故Q(t)在(0,1)上单调递增，当t∈(1,+∞)时，Q′(t)>0，故Q(t)在(1,+∞)上单调递增.

对于t∈(1,+∞)，Q(t)>Q(1)=0，

令t=t2，则有Q(t2)>0,即m(t2)-m(2-t2)>0，

所以m(t2)>m(2-t2),

由于t1,t2满足m(t1)=m(t2)=a+1,

则有m(t1)=m(t2)>m(2-t2)，

由于0

同时m(t)在(-∞,1)上单调递增,

故t1>2-t2，即t1+t2>2，因此x1x2>e2.

【评析】此法通过换元转化结论，成为了标准的极值点偏移问题(两个零点或根的和式不等式)，看似过程复杂，但却揭示了解决极值点问题的“通性通法”，即“对数型函数的极值点偏移问题”可转化为“指数型的极值点偏移问题”，反之亦然.而构造“对称函数”也成为了解决此问题的常规方法，2010年天津理科21题，2016年全国Ⅰ卷理科21题即可用上述的方法处理！

综合对比2.4,2.5可以看到，极值点偏移问题多与指对数函数有关，故而函数的选取变得尤为重要.可以看到，函数中如果含有指数函数，考虑取对数、之后问题转化对数函数的处理会更加简洁，同时也可考虑使用“对数平均不等式”求解.

2.6 函数的选取与构造(三)

方法六:由1.2知函数h(x)=lnx-(a+1)x有两个不同的零点x1,x2，

故lnx1+lnx2=(a+1)(x1+x2)，

因此，要证x1x2>e2，

即证lnx1+lnx2>2，

只需证(a+1)(x1+x2)>2，

由于f(x1)=f(x2)=0，

【评析】此法选取的函数是原函数本身，含有了参数(有些问题是无法消去参数的)，需要考虑带参处理,这无疑加大了求解的难度.对于无法消去参数的问题来说，带着参数进行“对称化构造函数”“构造对数平均不等式”是解决问题的主流方法.

2.7 函数的选取与构造(四)

方法七:由1.2知，函数h(x)=lnx-(a+1)x有两个不同的零点x1,x2，

同时h(x1)=h(x2)=0,

因此,要证x1x2>e2，即证lnx1+lnx2>2，

3.极值点偏移问题方法的再验证——以 2021新高考Ⅰ卷压轴题为例

【例2】(2021·新高考Ⅰ卷·22)已知函数f(x)=x(1-lnx).

(1)讨论f(x)的单调性；

解：(1)f(x)=x(1-lnx)，则f′(x)=-lnx(x>0)，

令f′(x)>0得0

令f′(x)<0得x>1,

故f(x)在(0,1)上单调递增，在(1,+∞)上单调递减.

(2)证明：由blna-alnb=a-b，

先证x1+x2>2.

3.1 构造对称函数法

方法一：由(1)知f(x)在(0,1)上单调递增，在(1,+∞)上单调递减，令f(x1)=f(x2)=k，则直线y=k与函数f(x)有两个交点，横坐标分别为x1,x2，

结合f(x)的大致图象可设0

构造函数F(x)=f(x)-f(2-x)=x(1-lnx)-(2-x)[1-ln(2-x)],x∈(0,1),

F′(x)=-lnx-ln(2-x),故F′(x)>0在x∈(0,1)上恒成立，F(x)在(0,1)单调递增,

所以F(x)

则有f(x)

又因为f(x1)=f(x2)，所以f(x2)

又由于f(x)在(1,e)上单调递减，故有x2>2-x1，即x1+x2>2得证.

3.2 比值换元法

方法二：由3.1可知f(x1)=f(x2)，

故有x1(1-lnx1)=x2(1-lnx2),

设0

故有x1(1-lnx1)=tx1(1-lntx1)，

故要证x1+x2>2，即证x1+tx1>2，

即证(1+t)x1>2，即ln(1+t)+lnx1>ln2,

即证(t-1)ln(1+t)+t-tlnt-1>(t-1)ln2,

即证(t-1)ln(1+t)+(t-1)(1-ln2)-tlnt>0,

令g(t)=(t-1)ln(1+t)+(t-1)(1-ln2)-tlnt(t>1),

g′(t)>g′(1)=0,故g(t)在(1,+∞)上单调递增，

故g(t)>g(1)=0,

故x1+x2>2.

3.3 构造特殊函数+放缩法

故g(x)在(0,+∞)上单调递减，注意g(1)=0，

由于0

又因为f(x1)=f(x2)，

限于篇幅，对于x1+x2>2证明的其他方法以及x1+x2