基于非线性干扰观测器的AUV量化反馈滑模控制

2021-11-08武建国陈武进赵晓宇张桐瑞

水下无人系统学报 2021年5期

关键词：观测器滑模坐标系

武建国, 陈凯, 陈武进, 赵晓宇, 张桐瑞, 程涛

武建国1, 2, 陈凯1, 陈武进1, 赵晓宇1, 张桐瑞2, 程涛3

(1.河北工业大学机械学院, 天津, 300131; 2.天津瀚海蓝帆海洋科技有限公司, 天津, 300457; 3.秦皇岛耀华新材料有限公司, 河北秦皇岛, 066000)

自主水下航行器; 滑模控制; 轨迹跟踪; 非线性干扰观测器; 量化效应

0 引言

21世纪以来, 随着各国对海洋重视的日益提高, 自主水下航行器(autonomous undersea vehicle, AUV)被广泛应用于海洋环境观测、海洋资源调查和海洋安全防卫等领域[1]。AUV的轨迹跟踪控制作为海洋工程和控制领域的重要分支[2], 由于存在模型非线性、未知的水动力系数和复杂干扰等问题[3], AUV控制器设计成为AUV发展的关键技术。

滑模控制(sliding-mode control, SMC)法作为一种鲁棒控制方法, 在系统不确定性和抗干扰方面具有良好的处理能力[4]。Zhang等[5]提出一种新型2阶SMC对便携式AUV进行轨迹跟踪; 马利民[6]采用全局无抖振SMC实现了轨迹跟踪控制; Jiang等[7]提出一种新型SMC来解决高速AUV的运动控制; Flavia等[8]使用SMC法确保超驱动海上补给船动态定位的容错鲁棒控制; 潘无为等[9]将滑模控制器用于AUV自适应编队控制; 杨超等[10]设计了终端滑模控制器对AUV进行轨迹跟踪; Taha等[11]设计了一种自适应积分SMC法来跟踪虚拟船舶的期望路径。

上述提到的控制方法均未考虑量化。这是由于当系统中数字网络参与反馈回路时如果考虑量化, 将难以保持系统的稳定性。对于处理量化引起的影响, SMC是一种有效的鲁棒控制方法。Yan等[12]分析了量化对SMC系统的影响。Corra- dini等[13]利用时变滑模控制律研究了具有饱和量化的单输入单输出线性不确定控制系统的反馈稳定问题。薛艳梅等[14]针对量化器灵敏度参数不匹配的不确定线性系统, 研究监督策略下的量化反馈滑模稳定控制问题。Hao等[15]研究了状态和输入信号同时量化的不确定线性系统的鲁棒容错补偿控制问题。

在实际工程应用中, 由于状态变量需要量化并传输到控制器, 因此量化是AUV控制存在的潜在问题之一。文中针对具有状态和控制输入同时量化的AUV, 提出一种量化SMC方法。设计中采用了动态均匀量化方案, 构造了一个非线性观测器来估计未知扰动, 并将量化误差的界引入到滑模控制器的开关项中以处理量化影响。

1 模型建立

1.1 坐标系的建立及其转换关系

文中基于“云帆”AUV, 建立如图1所示AUV载体坐标系及惯性坐标系, 其中载体坐标系的原点与AUV的浮心重合。

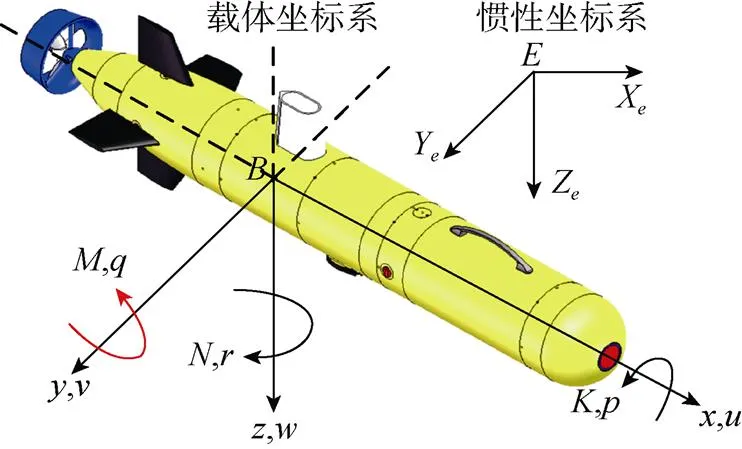
图1 AUV惯性和载体坐标系

两坐标系间的转换关系[16]

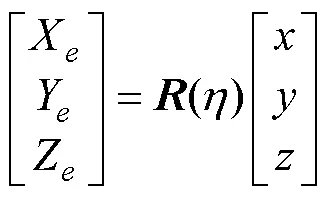
1.2 AUV动力学和运动学模型

AUV水平面的一般动态模型可以用进退、横荡和航偏来表示, 忽略潜浮、横滚和俯仰中的运动, 则AUV的运动学和动力学模型可表示为

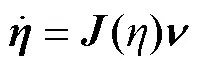
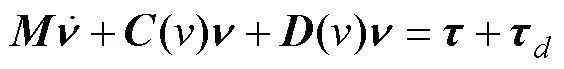
惯性矩阵

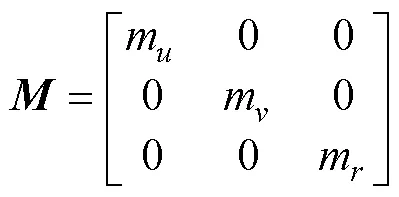
科氏力和向心力矩阵

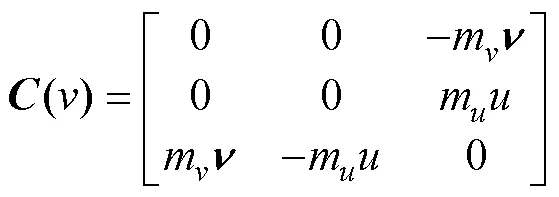
水动力阻尼矩阵

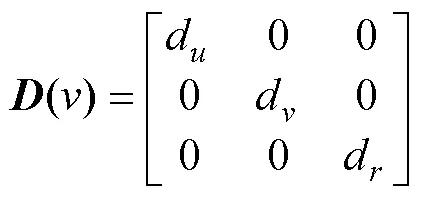
转换矩阵

1.3 AUV量化系统结构

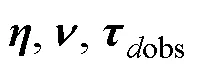
图2 AUV控制系统结构

假设AUV平台到控制器之间为动态均匀量化器, 并对量化参数进行离散调整。设计一种量化参数离散调整的动态均匀量化器, 一方面是因为它能将系统轨迹驱动到滑模面上, 而不仅仅是滑模面的某个邻域[17], 另一方面是离散调整策略更普遍, 在实际工程中更易于实施。在控制器到AUV平台之间采用静态均匀量化器, 具有结构简单而常见的优点。

2 AUV量化反馈滑模控制

文中首先给出非线性干扰观测器的设计, 然后用等效SMC方法对AUV系统进行无量化控制, 最后再给出有量化效应时的AUV控制系统。

2.1 非线性干扰观测器设计

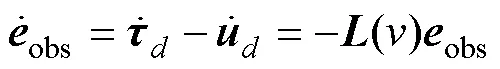
故非线性干扰观测器是稳定的。

则定义观测器的输出量

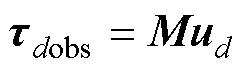
系统经过干扰观测器对外界干扰进行补偿后, 在经过SMC对未观测到的干扰及系统的不确定性部分进行补偿, 以更好地消除干扰, 实现稳定、快速的轨迹跟踪。

2.2 等效SMC

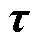
2.2.1 SMC

等效滑模控制率[19]设计为

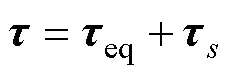
2.2.2 稳定性分析

联立式(4)、式(15)和式(16), 得

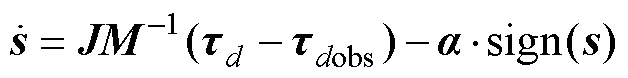
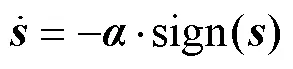
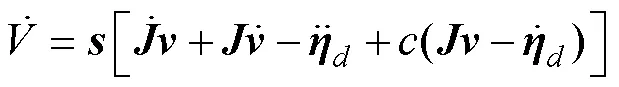
联立式(4)、式(18)和式(19), 得

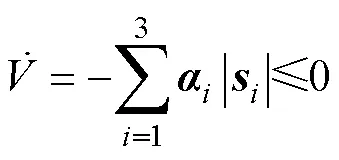
2.3 状态量化SMC

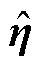
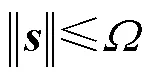
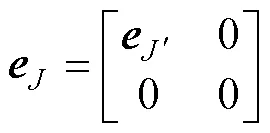
根据式(14)和式(21)得

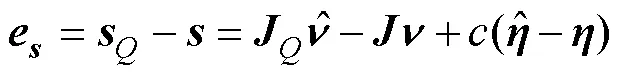
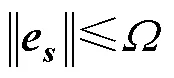
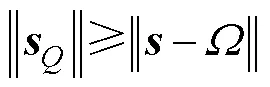
联立式(26)和式(27)得到式(22)。

证毕。

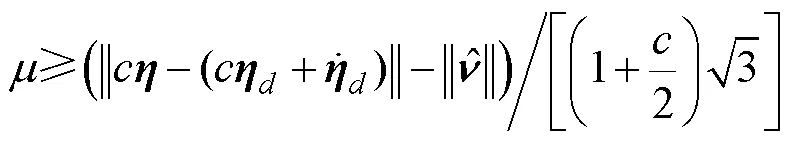
使用量化状态反馈, 式(4)可以写成

所以, 式(16)中的等效控制项可以写成

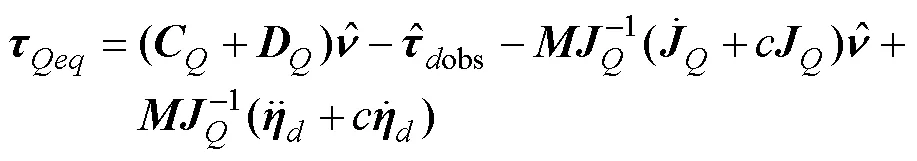
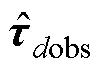
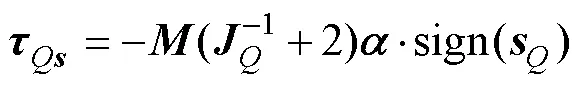
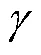
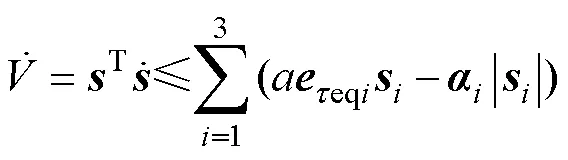
由式(16)和(30)得

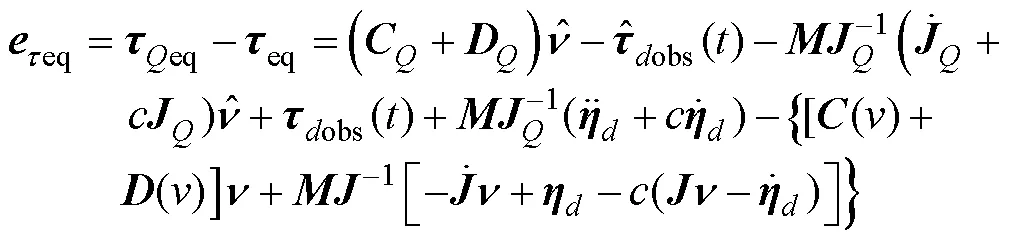
根据式(36)～式(39), 得

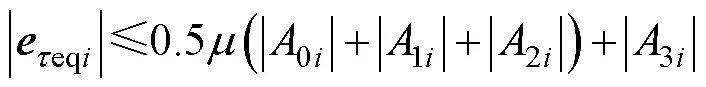
2.4 输入和状态量化SMC

给出类似于2.3节中AUV系统结果, 其状态和输入都被量化。

如图2所示, 输入量化控制率

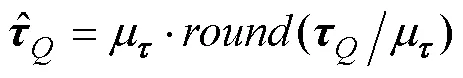
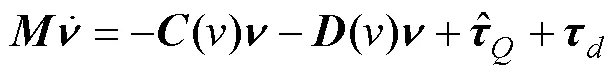
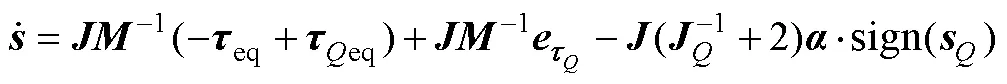
3 仿真与分析

3.1 余弦曲线轨迹跟踪

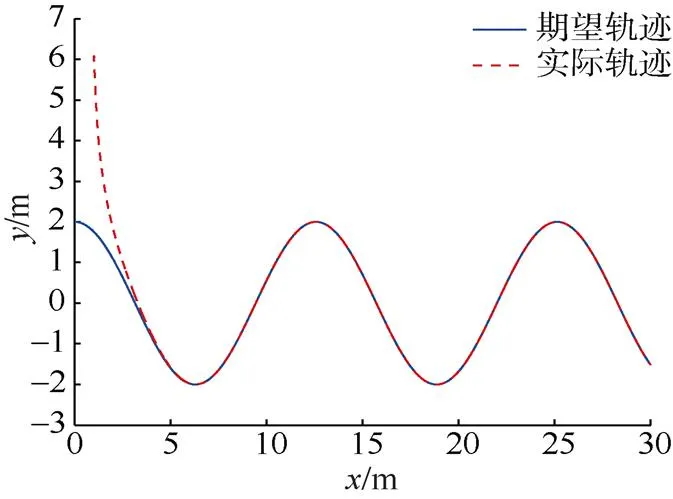
图3 余弦曲线期望轨迹和实际轨迹

图4 余弦曲线跟踪误差和随时间变化曲线

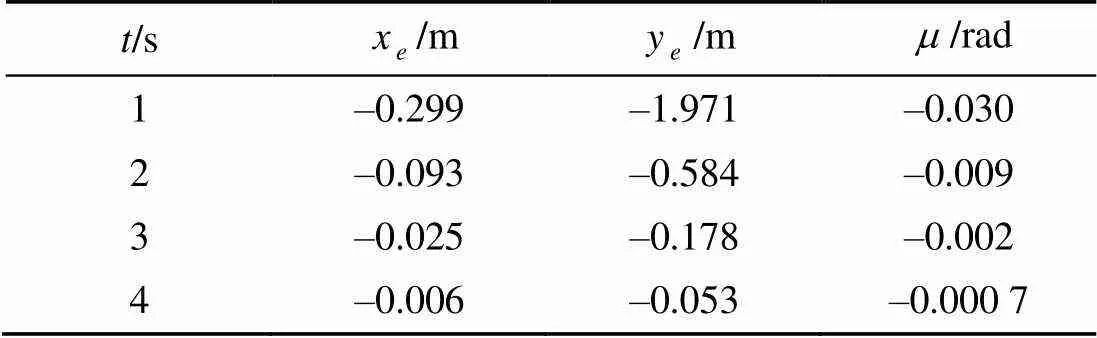
表2 AUV轨迹跟踪误差

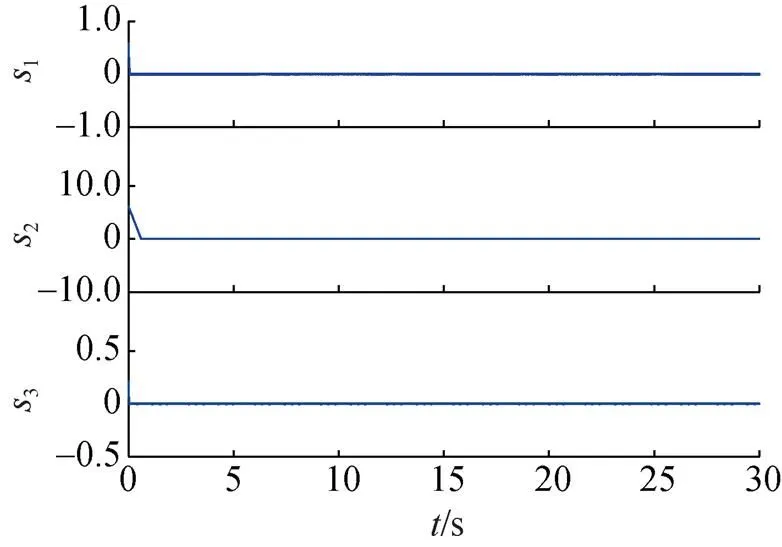
图5 滑模面的收敛曲线

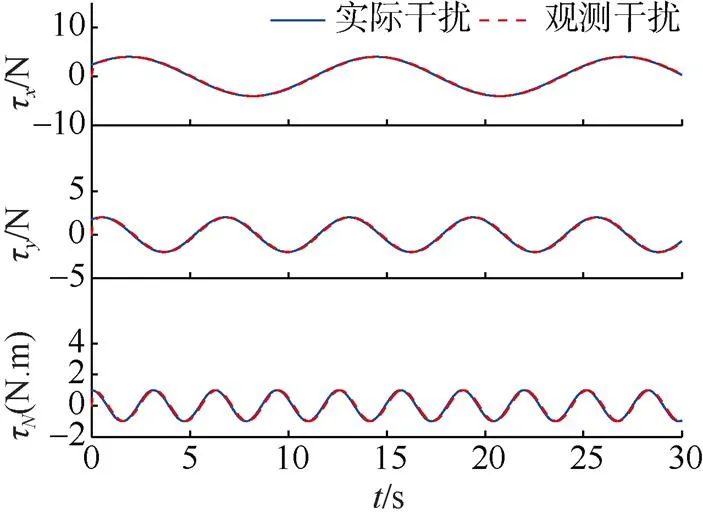
图6 复杂实际干扰和观测干扰变化曲线

图7 复杂干扰观测误差变化曲线

图8 量化参数变化曲线

3.2 四边形轨迹跟踪

表3 四边形期望轨迹参数表

图9 四边形期望轨迹与实际轨迹

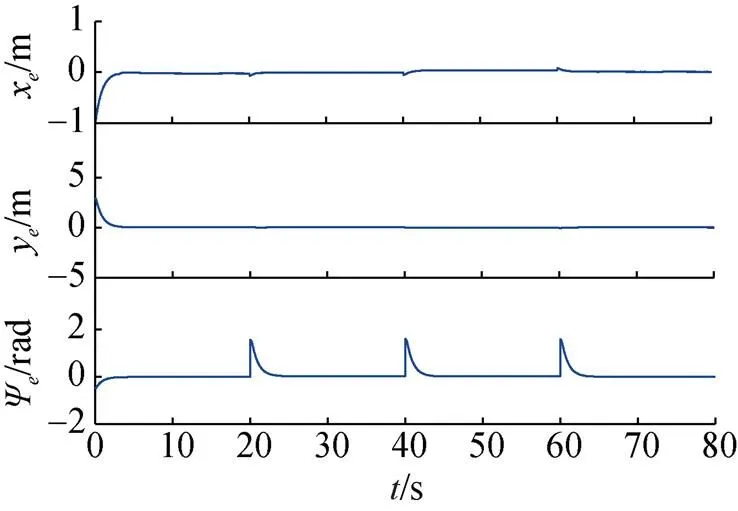
图10 四边形跟踪误差和随时间变化曲线

由图11～图12可知, 对于分段式干扰, 观测器也表现出良好的观测效果, 且观测误差只在分段式干扰交界处出现较大误差, 后续快速收敛于实际干扰。仿真结果验证了观测器的有效性。

图11 分段式实际干扰与观测干扰变化曲线

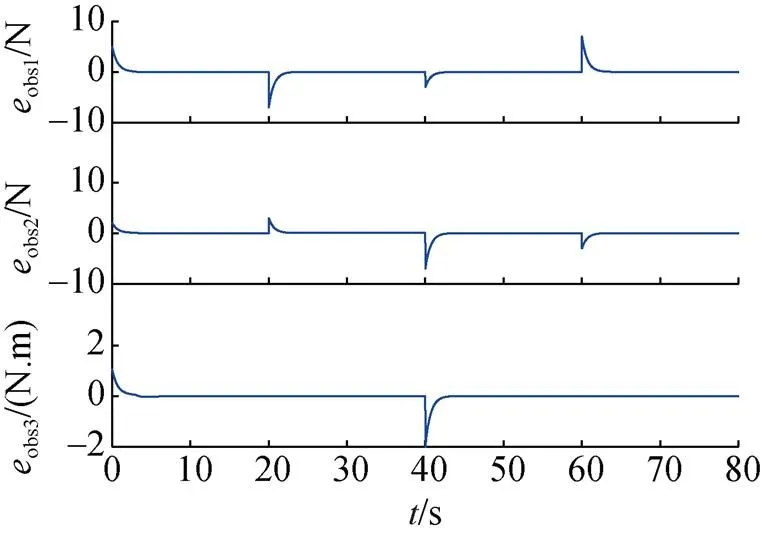
图12 分段式干扰观测误差变化曲线

4 结束语

[1] 黄琰, 李岩, 俞建成, 等.AUV智能化现状与发展趋势[J].机器人, 2020, 42(2): 215-231.

Huang Yan, Li Yan, Yu Jian-cheng, et al.State-of-the-Art and Development Trends of AUV Intelligence[J].Robot, 2020, 42(2): 215-231.

[2] Li S, Wang X.Finite-time Consensus and Collision Avoidance Control Algorithms for Multiple AUVs[J].Automatica, 2013, 49(11): 3359-3367.

[3] Xiang X, Yu C, Zhang Q.Robust Fuzzy 3D Path Following for Autonomous Underwater Vehicle Subject to Uncertainties[J].Computers & Operations Research, 2016, 84: 165-177.

[4] Yu X, Kaynak O.Sliding Mode Control Made Smarter: A Computational Intelligence Perspective[J].IEEE Systems, Man, and Cybernetics Magazine, 2017, 3(2): 31-34.

[5] Zhang G C, Huang H, Qin H D, et al.A Novel Adaptive Second Order Sliding Mode Path Following Control for a Portable AUV[J].Ocean Engineering, 2018, 151: 82-92.

[6] 马利民.欠驱动AUV全局无抖振滑模轨迹跟踪控制[J].智能系统学报, 2016, 11(2): 200-207.

Ma Li-min.Global Chattering-free Sliding Mode Trajectory Tracking Control of Underactuated Autonomous Underwater Vehicles[J].CAAI Transactions on Intelligent Systems, 2016, 11(2): 200-207.

[7] Jiang C M, Wan L, Sun Y S, et al.Design of Novel Sling-mode Controller for High-velocity AUV with Consideration of Residual Dead Load[J].Journal of Central South University, 2018, 25(1): 121-130.

[8] Flavia B, Gianluca I, Sauro L, et al.Advanced Control for Fault-tolerant Dynamic Positioning of an Offshore Supply Vessel[J].Ocean Engineering, 2015, 106: 472-484.

[9] 潘无为, 姜大鹏, 庞永杰, 等.相位耦合振子模型下的AUV自适应编队控制算法[J].哈尔滨工程大学学报, 2017, 38(1): 115-119.

Pan Wu-wei, Jiang Da-peng, Pang Yong-jie, et al.Adaptive Formation Control Algorithm for AUV on the Basis of the Coupled Phase Oscillator Model[J].Journal of Harbin Engineering University, 2017, 38(1): 115-119.

[10] 杨超, 郭佳, 张铭钧.基于RBF神经网络的作业型AUV自适应终端滑模控制方法及实验研究[J].机器人, 2018, 40(3): 336-345.

Yang Chao, Guo Jia, Zhang Ming-jun.Adaptive Terminal Sliding Mode Control Method Based on RBF Neural Network for Operational AUV and Its Experimental Research[J].Robot, 2018, 40(3): 336-345.

[11] Taha E, Mohamed Z, Kamal Y T.Terminal Sliding Mode Control for the Trajectory Tracking of Underactuated Autonomous Underwater Vehicles[J].Ocean Engineering, 2017, 129: 613-625.

[12] Yan Y, Yu X H, Sun C.Quantization Effect on Sliding Mode Control of Uncertain Dynamical Systems[J].Asian Journal of Control, 2016, 18(3): 1142-1146.

[13] Corradini M L, Orlando G.Robust Quantized Feedback Stabilization of Linear Systems[J].Automatica, 2008, 44(9): 2458-2462.

[14] 薛艳梅, 郝立颖.量化参数不匹配的线性系统监督滑模控制设计[J].计算机工程与应用, 2015, 51(15): 22-27.

Xue Yan-mei, Hao Li-ying.Supervisory-based Sliding Mode Control Design for a Class of Linear Systems Subject to Quantization Parameter Mismatch[J].Computer Engineering and Applications, 2015, 51(15): 22-27.

[15] Hao L Y, Yang G H.Robust Fault Tolerant Control Based on Sliding Mode Method for Uncertain Linear Systems with Quantization[J].ISA transactions, 2013, 227(9): 692- 703.

[16] Tabataba’i-Nasab, Fahimeh S, Keymasi K A, et al.Adaptive Nonlinear Control of an Autonomous Underwater Vehicle[J].Transactions of the Institute of Measurement and Control, 2019, 41(11): 3121-3131.

[17] Zheng B C, Yang G H.Quantized Output Feedback Stabilization of Uncertain Systems with Input Nonlin-earities Via Sliding Mode Control[J].International Journal of Robust and Nonlinear Control, 2014, 24(2): 228-246.

[18] Chen W H.Disturbance Observer Based Control for Nonlinear Systems[J].IEEE/ASME Transactions on Mecha- tronics, 2004, 10(4): 706-710.

[19] Utkin V.Variable Structure Systems with Sliding Mod- es[J].IEEE Transactions on Automatic Control, 1977, 22(2): 212-222.

Quantized Feedback Sliding Mode Control for AUV Based on Nonlinear Disturbance Observer

WU Jian-guo1, 2, CHEN Kai1, CHEN Wu-jin1, ZHAO Xiao-yu1, ZHANG Tong-rui2, CHENG Tao3

(1.Hebei University of Technology, Tianjin 300131, China; 2.Tianjin Hanhai Lanfan Marine Technology Co., Ltd., Tianjin 300457, China; 3.Qinhuangdao Yaohua New Materail Co., Ltd., Qinhuangdao 066000, China)