鱼雷湿模态仿真与试验分析
2021-11-08王红瑞单志雄
赵 琪, 郭 君, 曹 栋, 王红瑞, 单志雄
鱼雷湿模态仿真与试验分析
赵 琪1, 郭 君1, 曹 栋2, 王红瑞1, 单志雄1
(1.中国船舶集团有限公司 第705研究所, 陕西 西安, 710077; 2.中国船舶集团有限公司 第12研究所, 陕西 西安, 713100)
以典型鱼雷结构为基础, 首先通过干模态试验与仿真分析, 修正全雷有限元模型, 然后利用LMS Virtual.Lab边界元流固耦合分析方法, 进行全雷湿模态仿真。分析结果表明, 与在空气中相比, 鱼雷结构在水中各阶固有频率均有所降低, 前3阶频率降低量在35%左右。通过全雷干、湿模态仿真分析, 获得解决复杂流固耦合问题的新途径, 为后续进行鱼雷结构优化、减振降噪设计等提供参考。
鱼雷; 干模态; 湿模态; 边界元法; 流固耦合
0 引言
模态分析主要用于确定结构的振动特性(包括固有频率和振型), 是进行其他动力学分析的基础。对结构进行模态分析需要考虑结构所处的环境, 若在空气环境中(即干模态), 由于空气对结构的影响较小, 通常在试验和仿真分析中可忽略; 若在水下环境中(即湿模态), 环境产生的预应力效应和振动时的流固耦合效应会对模态产生影响, 所以结构的湿模态分析就不能忽略流体环境的影响。湿模态在水下航行器的设计中占有较大比重, 近年来日益受到工程界和学术界的重视[1]。
目前, 由于水下试验的准备和实施比较繁琐, 且试验成本高, 对结构湿模态的数据获取多利用仿真分析的方法。王聪等[2]基于流固耦合及模态理论, 对导弹缩比模型进行了干、湿模态的研究, 分析认为附连水质量引起的结构模态质量的增加对结构低阶弯曲模态频率的影响较为显著。黄晓明等[3]对船体结构在无限水域中垂向低阶湿模态特性进行了仿真研究, 发现使用无封盖水域能在合理计算资源下得到精确的计算结果。陈东阳等[4]基于声固耦合模型对考虑水介质、顶张力情况下的立管进行湿模态计算, 结果表明湿模态频率比干模态小, 且随着顶张力的增大而增大, 静水压力和瞬态流场载荷使湿模态频率略微增加。崔高伟等[5]针对液体燃料对火箭结构的模态影响, 基于软件MD.Nastran平台, 利用虚质量法进行模态分析, 研究液体对火箭结构动态特性的影响。何孔德等[6]利用流场中结构模态计算方法, 结合流体力学方程组, 推导出浮筒在水下的虚拟质量矩阵, 实现了考虑水作用的浮筒固有特性分析。
文中的研究对象是典型轻型鱼雷, 通过对鱼雷模拟结构的干模态试验与仿真分析, 修正和验证全雷分析模型, 利用LMS Virtual.Lab中边界元的流固耦合分析方法, 研究鱼雷湿模态特性, 为复杂流固耦合的动力学问题提供新的解决途径。
1 模态分析基本原理
1.1 干模态分析
模态分析是指将线性定常系统的振动微分方程组中的物理坐标转换为模态坐标, 使方程组解耦, 成为一组以模态坐标及模态参数描述的独立方程, 从而求出系统的模态参数。
线性结构系统(一般粘性阻尼系统)的振动微分方程为
对于低阻尼材料, 忽略系统阻尼, 当外部激励力为零时, 可得系统自由振动微分方程为

设式(1)的特解为
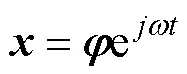
将式(3)代入式(2)得
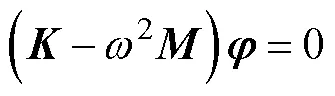
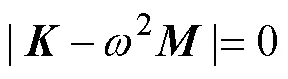
1.2 湿模态分析
鱼雷在水下环境中始终与水接触, 由于受到水压力的作用, 结构的模态会有较大变化。结构与流体的相互作用构成一个流固耦合系统, 在耦合作用下, 结构振动会产生流体负载, 而受到扰动的流体会同时对结构产生一个附加力, 所以必须同时计算结构动力学方程和流体域的波动方程。
根据波动理论, 得到三维波动方程为

利用Galerkin方法, 得出流体域内的方程为
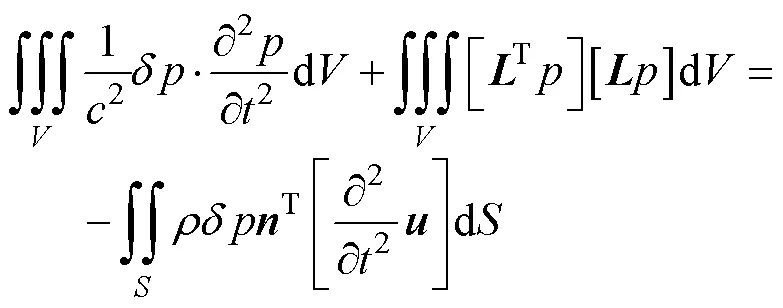
式(7)经离散变换后用矩阵形式表达为
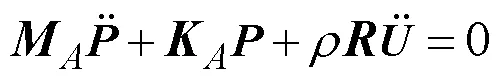
根据Hamilton原理, 结合式(1)可得流体中弹性壳体耦合的动力学方程为
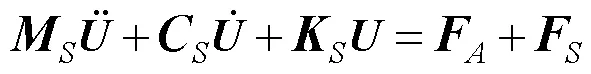
结合式(8)和式(9), 可得流固耦合方程的统一矩阵形式为
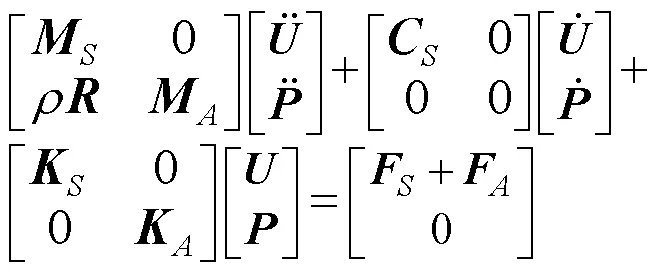
按照对式(1)方法, 对式(10)进行求解, 即可得到系统的耦合模态频率及对应的模态振型。
2 干模态试验及仿真分析
2.1 干模态试验
典型鱼雷模拟结构外径324 mm、长度约3 000 mm, 是由头段、前段、中段、后段及组件模拟件、连接楔环组成的圆柱状结构。干模态试验的目的是测试结构前3阶弯曲模态, 以实验数据验证和修正仿真分析模型, 为后续的结构改进设计提供依据。干模态试验基于LMS动态测试分析系统, 测点布置在雷体正上方母线处(测点A系列)和雷体侧方(测点B系列), 各测点轴向位置保持一致, 具体如图1所示。试验系统在全雷重心位置用弹性橡胶绳悬吊, 预测试橡胶绳悬挂系统的固有频率为1.5 Hz, 支持方式为自由-自由方式。试验中传感器安装如图2所示。
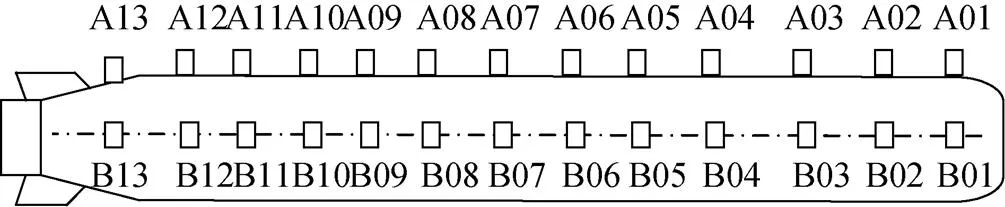
图1 测点分布

图2 干模态试验
模态试验采用单点脉冲击振及时域多自由度模态分析方法。激励位置选在A01点附近, 得到全雷前3阶弯曲模态固有频率如表1所示。从表中可以看出,向和向的弯曲模态频率基本一致, 其对应的模态振型也一致。此处仅列出向对应振型如图3所示。

表1 干模态试验频率
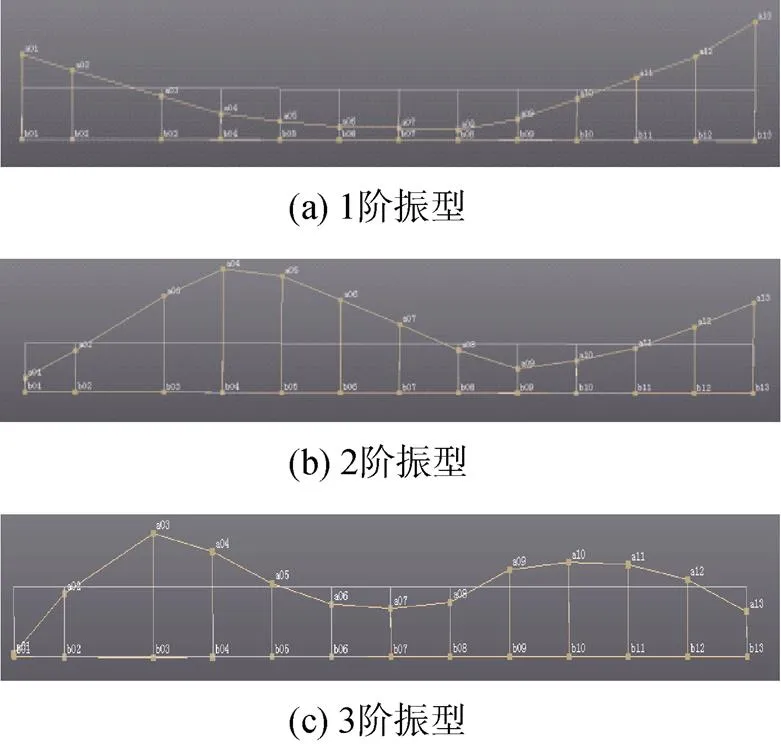
图3 干模态试验前3阶振型
2.2 建立仿真分析模型
以结构模型为基础, 建立鱼雷全尺寸有限元分析模型。在不影响模态计算结果的前提下, 对内部各组件进行简化处理, 简化遵照以下原则:
1) 忽略各组件小开孔、小倒角等不影响模态计算结果的细节特征;
2) 忽略安装螺钉等连接结构;
3) 忽略组件内部结构, 以质量模拟件实体建模;
4) 忽略电缆与接插件等刚度较小的结构;
e) 通过壳体上的开孔及凸台与壳体安装的组件, 其与壳体连接部分通过布尔运算归为壳体组件, 剩余部分归为组件部分。
当完成组件的网格划分后, 对生成的结构化体网格的质量进行检查, 要求网格的雅克比系数大于0.7, 最大角度小于120°, 最小角度大于20°。当网格的质量不满足要求时, 需修改网格划分参数, 重新对组件的网格进行划分直至满足要求。
同时为提高计算效率, 减小局部组件模态对整体模态的影响, 除对舱段刚度影响较大的组件外, 其他组件利用质量单元代替, 质量单元的位置位于该组件的质心位置。
鱼雷各舱段间由楔环连接, 楔环连接形式复杂, 其连接刚度对雷体模态分析的影响较大,参考文献[7]和文献[8]中对鱼雷楔环的处理方式, 在全雷建模时, 在段间连接处用等效刚度的模型进行处理。按照上述方法建立的有限元模型如图4所示。全雷前3阶弯曲模态振型如图5所示。

图4 全雷有限元模型
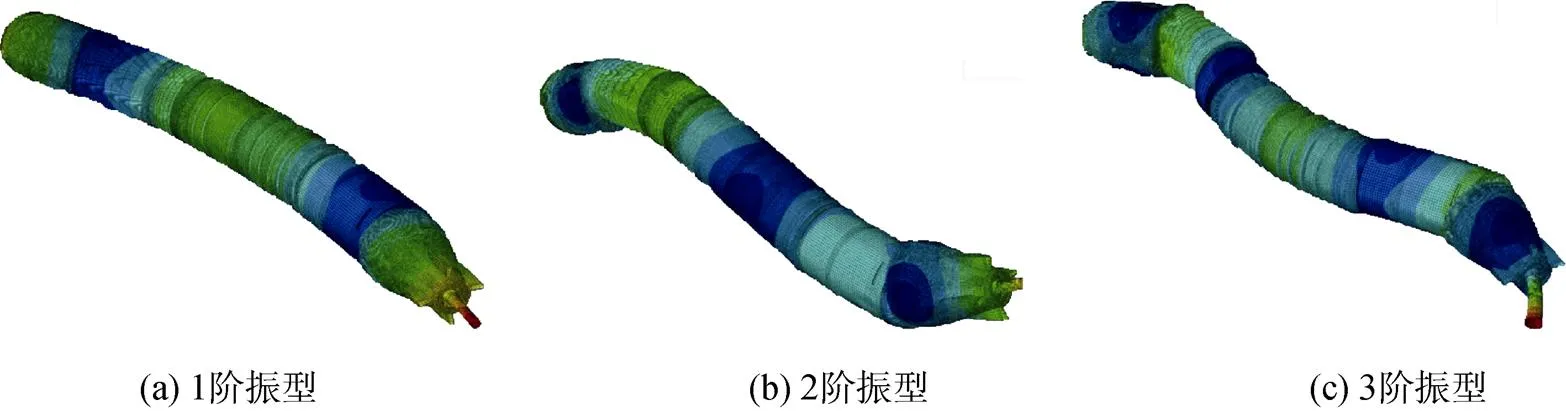
图5 干模态仿真前3阶振型
将仿真计算结果与试验结果相比较, 具体如表2所示。从表中可以看出, 1阶弯曲模态与试验结果非常接近, 2阶弯曲模态结果与试验结果的相对误差为4.8%, 3阶弯曲模态的计算结果的相对误差为12.8%。表明该模型可进一步用于湿模态仿真分析。

表2 干模态试验与仿真结果对比
3 湿模态仿真分析
在进行流固耦合模态分析计算时, 结构与流体拥有各自的网格属性。为了便于计算, 这些网格间通常要转移数据或建立耦合关系, 但是不同网格间的节点和单元通常不是一一对应的, 因此需要定义网格间的映射关系。采用LMS Virtual.Lab分析模块中的耦合模态求解器进行湿模态的求解。在LMS Virtual.Lab中, 使用边界元的方法进行耦合模态计算, 需要先进行干模态分析, 其次要准确提取结构与流体的耦合面, 进行耦合面的网格映射, 结合干模态分析结果与耦合面的映射关系, 进行水下耦合模态的计算。
流固耦合的目的是为了让欧拉网格中定义的材料(流体)与拉格朗日网格定义的材料(结构)发生相互作用。如果不定义耦合关系, 即使拉格朗日单元恰好处在欧拉网格范围内, 也不会对欧拉材料的流动产生任何影响, 同时自身也不会受到来自欧拉材料的力的作用[8]。要在结构与流体之间建立耦合关系, 首先要在结构上定义一层耦合面, 该面是结构与流体之间的相互作用力的传递者。对于流体, 该面可充当流场边界; 同时, 流场的作用力使得有力作用在耦合面上, 引起结构单元的变形。
为建立结构网格与水域网格的耦合关系, 首先需提取雷体表面结构的网格单元, 具体如图6所示。

图6 雷体表面结构网格
其次将提取的结构网格按照耦合映射关系转化为水域边界网格, 如图7所示, 从图中可以看出, 网格数量明显降低。

图7 流固耦合面的网格映射
建立起耦合面的网格映射关系后, 以耦合面网格为中心, 建立水域网格, 如图8所示。在水域中沿结构长度方向的网格数取20~80, 水域径向网格尺度小于结构界面特征尺度的1/2时, 能获得较为精确的计算结果。结构化六面体网格划分方式能获得较高的计算精度。因而对于流固系统, 应优先使用结构化六面体网格划分方法。
基于干模态分析结果, 结合水域耦合关系, 计算全雷水下环境前3阶弯曲模态频率及振型如图9所示。
对比以上干模态、湿模态分析结果, 如表3所示。可以看出, 各阶湿模态频率比干模态频率均有所下降, 频率降低量在35%左右, 该结果与船舶工程领域的经验数据较为接近, 即湿模态比干模态频率下降约30%[9]。

图8 水域网格
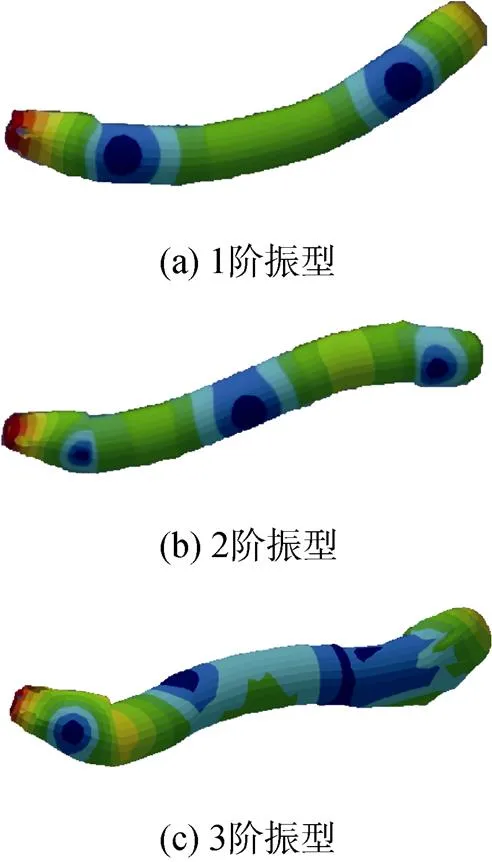
图9 湿模态仿真前3阶振型
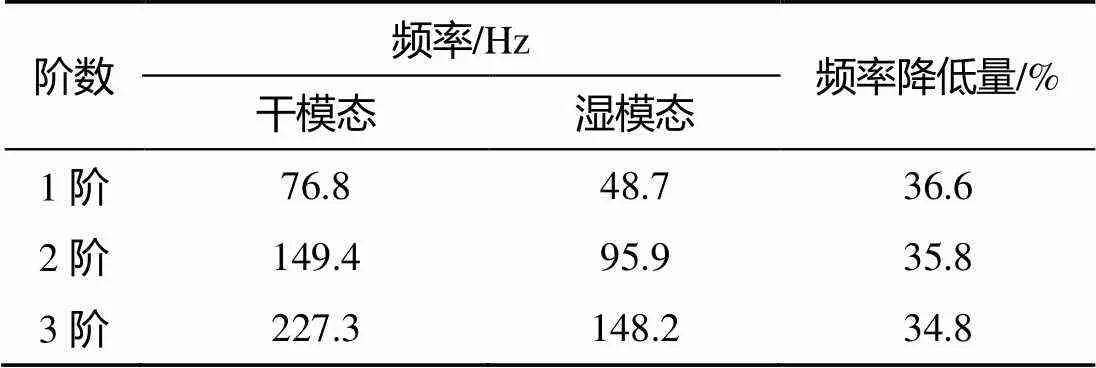
表3 干模态与湿模态仿真结果对比
4 结束语
文中对典型鱼雷结构进行了干模态试验与仿真分析, 得到修正的全雷有限元模型, 再利用LMS Virtual.Lab中边界元的流固耦合分析的方法, 完成了全雷湿模态仿真分析, 得到有参考意义的模态数据。结构在水中与在空气中相比, 各阶固有频率均有所降低, 前3阶频率降低量在35%左右, 说明环境介质对系统的振动频率影响显著。而针对鱼雷湿模态, 文中提出结构-流体组合模型中耦合面的网格映射方式, 为解决流固耦合下的动力学问题, 提出新的解决途径。
全雷结构为复杂装配体, 在后续研究中, 需建立精细化模型, 分析各组件、段间楔环等对全装配结构模态的贡献量。在结构设计时需要考虑由于环境不同而引起的振动特性参数的变化, 这在结构总体系统设计、动力参数设计、减振降噪设计等方面尤为重要。
[1] 胡会朋, 卢丙举, 秦丽萍.预应力和流固耦合效应对水下壳结构振动特性影响研究[J].舰船科学技术, 2017, 39(8): 47-50.
w Hu Hui-peng, Lu Bing-ju, Qin Li-ping.The Study of Effects of Pre-stress and Fluid-solid Interaction Effect on Vibration Properties of Underwater Shell Structures[J].Ship Science and Technology, 2002, 39(8): 47-50.
[2] 王聪, 王莉, 王学孝, 等.导弹模拟件水下动态特性试验研究[J].哈尔滨工业大学学报, 2002, 34(3): 392-395.
Wang Cong, Wang Li, Wang Xue-xiao, et al.Dynamic Characteristics of Model Missile Under Water[J].Journal of Harbin Institute of Technology, 2002, 34(3): 392-395.
[3] 黄晓明, 朱锡, 牟金磊, 等.整体结构模型低阶湿模态仿真计算方法[J].舰船科学技术, 2011, 33(5): 9-12.
Huang Xiao-ming, Zhu Xi, Mu Jin-lei, et al.Simulation and Experimental Investigation on Transverse Lower Order Wet Mode of Whole Structure Model[J].Ship Science and Technology, 2011, 33(5): 9-12.
[4] 陈东阳, Laith K A, 王国平, 等.流场环境对柔性立管湿模态的影响[J].哈尔滨工程大学学报, 2017, 38(10): 1587-1594.
Chen Dong-yang, Laith K A, Wang Guo-ping, et al.Influence of Flow Field Environment on Wet Modal Vibration of Flexible Riser[J].Journal of Harbin Engineering University, 2017, 38(10): 1587-1594.
[5] 崔高伟, 洪良友, 张冬梅.虚拟质量法在运载火箭模态分析中的应用[J].强度与环境, 2013, 40(5): 43-47.
Cui Gao-wei, Hong Liang-you, Zhang Dong-mei.The Application of Virtual Mass Method in Modal Analysis of the Rocket[J].Structure & Environment Engineering, 2013, 40(5): 43-47.
[6] 何孔德, 方子帆, 燕怒, 等.基于虚拟质量法的水下浮筒流固耦合动态特性分析[J].科学技术与工程, 2013, 13(25): 7497-7500.
He Kong-de, Fang Zi-fan, Yan Nu, et al.The Dynamic Response Analysis of Fluid-solid Coupling Properties for Underwater Buoy Based on Virtual Mass[J].Science Technology and Engineeing, 2013, 13(25): 7497-7500.
[7] 刘晓欧, 尹韶平, 严光洪.基于MSC Nastran的水下环肋圆柱壳体振动模态计算方法[J].计算机辅助工程, 2006, 15(z1): 124-127.
Liu Xiao-ou, Yin Shao-ping, Yan Guang-hong.Underwater Vibration Modal Calculation of the Ring-stiffened Cylindrical Shell with MSC Nastran[J].Computer Aided Engineerin, 2006, 15(z1): 124-127.
[8] 马锐磊, 尹韶平, 曹小娟, 等.鱼雷楔环连接结构等效刚度建模与模态分析[J].舰船科学技术, 2014, 32(2): 143-147.
Ma Rui-lei, Yin Shao-ping, Cao Xiao-juan, et al.Research on Finite Element Modeling and Modal Analysis of Torpedo’s Wedged-ring Connection Structure[J].Ship Science and Technology, 2014, 32(2): 143-147.
[9] Everstine F C.A Symmetric Potential Formulation for Fluid-Structure Interaction[J].Journal of Sound and Vibration, 1981, 79(1): 157-160.
Simulation and Test of Wet Modalof a Torpedo
ZHAO Qi1, GUO Jun1, CAO Dong2, WANG Hong-rui1, SHAN Zhi-xiong1
(1.The 705 Research Institute, China State Shipbuilding Corporation Limited, Xi’an 710077, China; 2.The 12 Research Institute, China State Shipbuilding Corporation Limited, Xi’an 713100, China)
The finite element model of a typical torpedo structure is first modified by conducting a dry modal test and simulation analysis.Then, the LMS Virtual Lab boundary element fluid-solid coupling analysis method is used in the wet modal simulation analysis of the entire torpedo.The analysis results show that the inherent frequency of torpedo structure is reduced in all orders in water, with the first 3rd order decreasing by approximately 35% compared to that in air.New methodologies for solving complex fluid-solid coupling problems are achieved through the dry and wet modal simulation analysis, which can be used as a reference for torpedo structure optimization and noise reduction design.
torpedo; dry modal; wet modal; boundary element method; fluid-structure interaction
赵琪, 郭君, 曹栋, 等.鱼雷湿模态仿真与试验分析[J].水下无人系统学报, 2021, 29(5): 550-555.
TJ630.1; TB71.2
A
2096-3920(2021)05-0550-06
10.11993/j.issn.2096-3920.2021.05.006
2020-11-09;
2020-12-18.
赵 琪(1989-), 男, 硕士, 工程师, 主要研究方向为鱼雷总体技术.
(责任编辑: 许 妍)
