基于瑞利-均匀分布的AUV应召搜索目标散布区域估计方法
2021-11-08崔东华纪秀美代志恒王团盟
崔东华, 纪秀美, 代志恒, 王团盟
基于瑞利-均匀分布的AUV应召搜索目标散布区域估计方法
崔东华1, 2, 纪秀美3, 代志恒4, 王团盟5
(1. 中国人民解放军91054部队, 北京, 443500; 2. 北京理工大学 信息与电子学院, 北京, 100081; 3. 中国人民解放军31002部队, 北京, 443500; 4. 中国船舶集团有限公司 第716研究所, 江苏 连云港, 222006; 4. 中国船舶集团有限公司 第705研究所, 陕西 西安, 710077)
在自主水下航行器(AUV)执行应召搜索任务过程中, 目标的散布区域是引导平台对AUV航路规划的重要依据。通过信息搜集的目标初始位置误差散布及其运动参数误差散布导致目标运动过程中任意时刻的位置分布函数表现出非正态分布和非均匀分布的特点, 然而, 现有方法对这一问题的描述往往过于简单甚至不尽合理, 由此在研究类似搜索路径规划和搜索概率计算等问题时造成与实际不相符的现象。为解决AUV应召搜索时目标散布区域的估计问题, 在建立目标初始位置散布区域估计模型的基础上,根据目标速度和航向等运动参数误差散布规律, 建立了目标运动过程中位置散布区域的瑞利-均匀联合估计模型。仿真试验结果表明, 该方法与传统二维正态分布方法相比更为合理实用, 对目标散布位置的估计更为准确, 便于数值分析与工程应用。
自主水下航行器; 应召搜索; 目标散布区域; 瑞利-均匀联合估计
0 引言
利用自主水下航行器(autonomous undersea vehicle, AUV)执行应召搜索任务是指通过获得的目标位置及其运动参数等概略信息, 引导距离目标较远、以水下隐蔽状态航行的AUV航行至目标曾经或将要出现的海域对目标实施搜索发现的任务过程。为了保持自身的隐蔽性, 执行搜索任务时, AUV通常必须以水下航行状态、使用被动方式对目标实施搜索探测。但AUV的搜索速度相对较慢、探测距离相对较小, 这就决定了完成这一任务通常需要一个较长的时间过程[1-4]。
由情报获取的目标初始位置误差散布和其运动参数误差散布的综合影响必然导致任意时刻目标位置呈现一定的分布[5-6], 而且这种分布是遵循一定规律的动态位置分布。在对AUV实施规划时, 如果不能依据这种分布规律规划其搜索路径, 把搜索平台引导到目标散布概率高的区域范围进行搜索, 就会由于目标自身运动而产生的位置变化范围不同而使AUV发现目标的概率大打折扣。
因此, 目标位置和运动参数的不确定性决定了目标散步区域的不确定性, 而目标的散布区域是引导平台对AUV航路规划的重要依据。
当利用统计学方法对目标位置的这种不确定性进行描述时, 必须首先依据目标初始位置和运动参数的散布规律, 估计当前时刻的目标位置散布。但是, 目前在研究搜索路径规划以及搜索效能评估的各种文献中, 普遍存在着对目标位置散布的假设条件不甚合理或过于简单的情况。例如, 在应召搜索的应用中, 往往仅考虑目标以确定的航速航行, 且假设目标的位置在与其速度成比例增长的圆内呈均匀分布[7]; 或在考虑目标以确定的速度航行时, 又简单地假设目标的位置在因应召时间出现的散布圆内呈正态分布[8-9]; 也有的在研究搜索概率时完全不考虑目标初始位置散布的情况。这些处理方法由于与实际目标位置的散布存在较大差距, 必然造成与实际应用不相符的问题。
对此, 文中依据任意时刻目标位置散布规律将受到其初始位置散布和运动参数散布规律联合影响的实际, 在建立目标初始位置散布区域估计模型的基础上, 根据目标速度和航向等运动参数误差散布规律, 研究并建立目标运动过程中其位置散布区域的联合估计模型。以期为执行应召搜索任务的AUV提供更为精准的航路规划信息, 提高应召搜索的发现概率。
1 目标位置动态散布区域建模
在以上应用范畴中, 通常假设目标在水平面内做等速等向运动,0时刻引导平台发现目标处于初始位置(0,0)上, 由于目标初始位置及其运动参数(速度和航向)均存在一定分布规律的误差, 为了将AUV引导到目标附近, 就必须通过目标初始位置及其运动参数误差的分布规律估计未来某时刻目标位置散布, 即目标位置动态散布。
1.1 目标初始位置散布
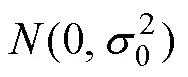
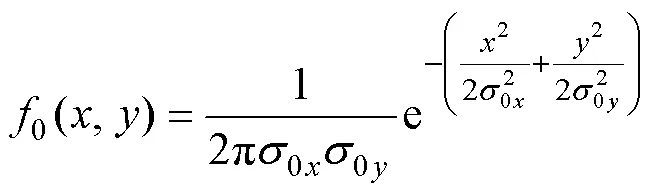
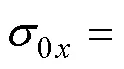
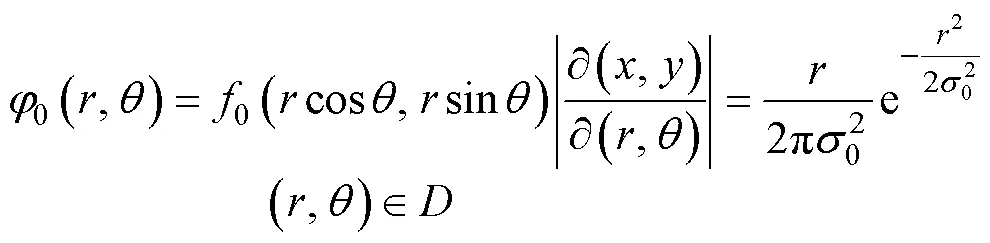
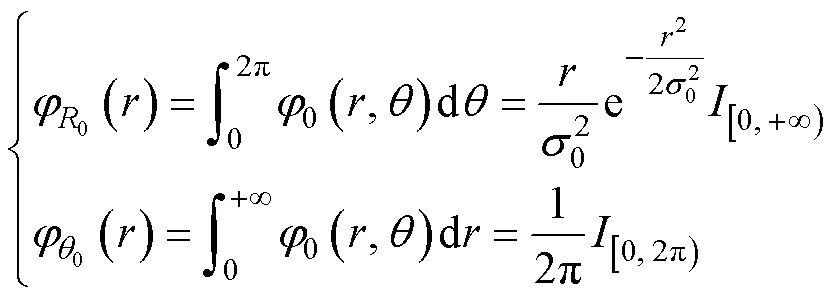
式中,为单位函数。
1.2 目标运动位置散布
除了目标初始位置散布影响之外, 一定时间后, 目标运动参数的不确定性也将使t时刻目标位置呈现随机变化, 进而对目标位置分布产生一定的影响。因此, 目标位置动态散布是由初始位置散布和运动参数散布两部分构成。
以下针对情报获取目标运动参数的3种最常见情况, 研究目标位置动态散布的估计问题。
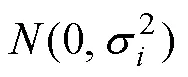
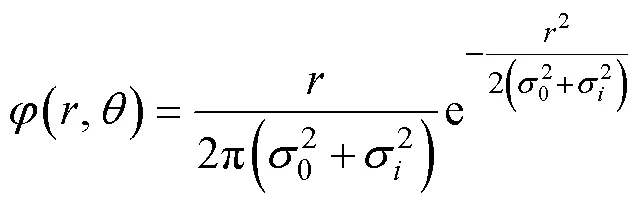
按式(3)可得因目标速度和航向不确定性引起的目标位置散布概率密度函数在极坐标下的表达式为
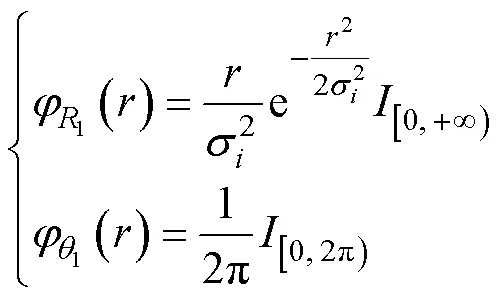
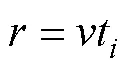
此时, 由式(5)可求得目标速度的概率密度函数为
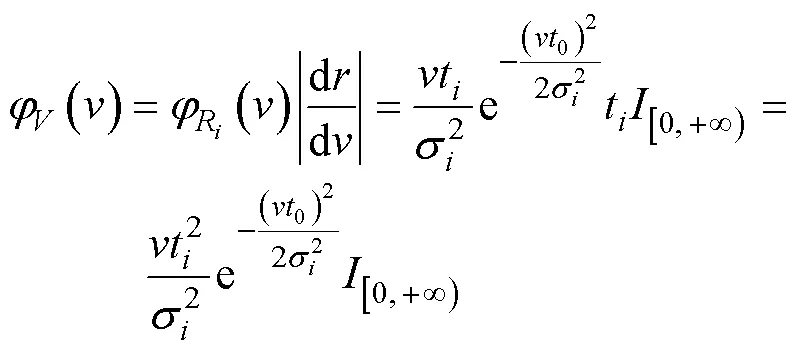
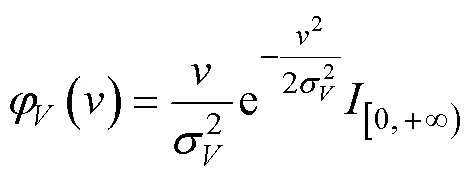
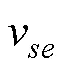
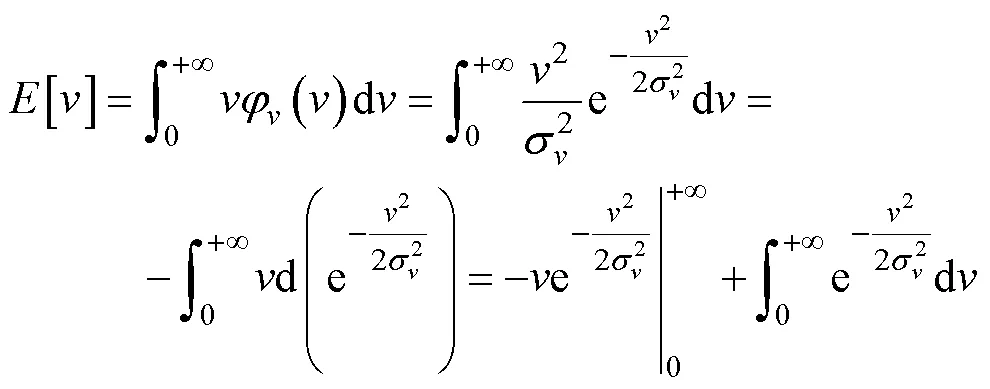
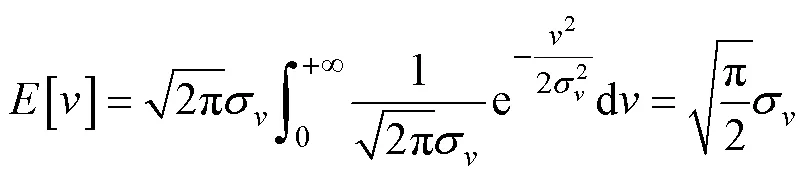
于是
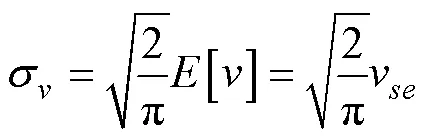
从而
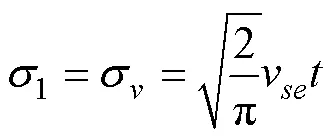
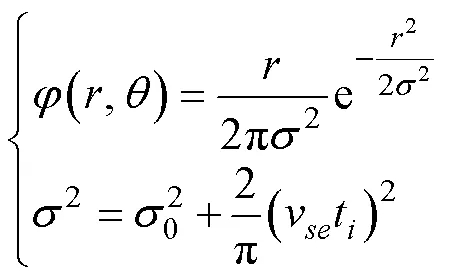
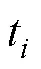
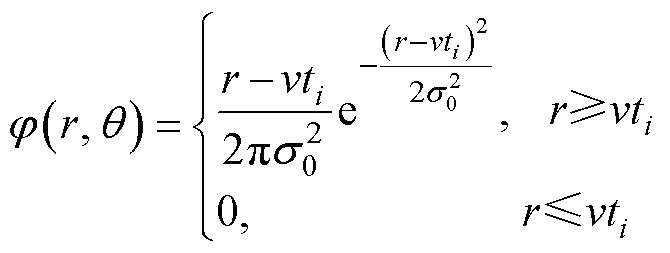
3) 目标速度和概略航向已知
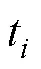
由于目标速度已知, 所以其位置的距离散布概率密度函数同式(13)。


故
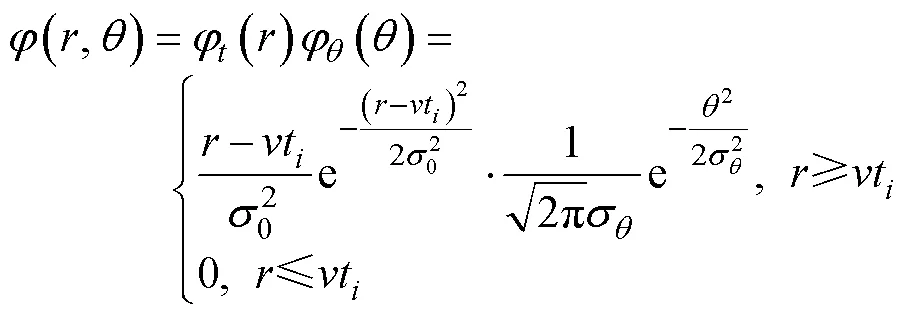
2 实验验证
为了验证上述模型的合理性, 针对既定的典型战场态势, 采用仿真方法分别将文中提出的瑞利-均匀联合分布算法与文献[8]和[9]中提出的联合正态分布算法和蒙特卡洛统计法进行对比, 以验证算法的性能。
2.1 目标初始位置散布
2.2 算法性能对比
1) 目标初始位置估计
目前各种文献假设目标初始和运动过程中的散布均服从直角坐标系下二维正态分布[6,8-9], 按式(1)仿真绘制基于联合正态分布的目标初始位置散布概率密度函数, 如图1所示。
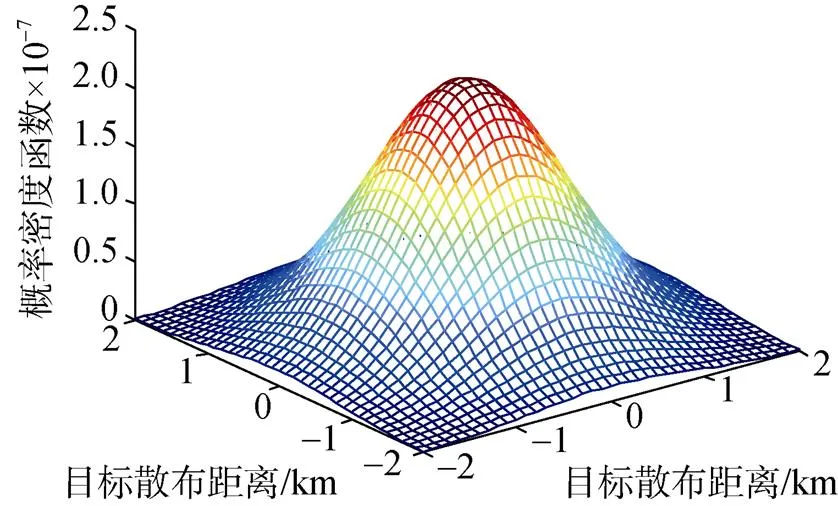
图1 基于二维正态分布的目标初始位置散布概率密度函数
文中在二维联合正态分布的基础上, 推导出目标初始位置散布服从极坐标系下瑞利-均匀分布概率密度函数(式(3))。
为了将二维正态分布与瑞利-均匀分布这2种描述目标散布概率密度函数算法进行比对, 将按概率密度函数生成的目标散布统一在直角坐标系下绘图, 2种方法的仿真结果如图2所示。仿真结果表明2种方法的计算结果一致。
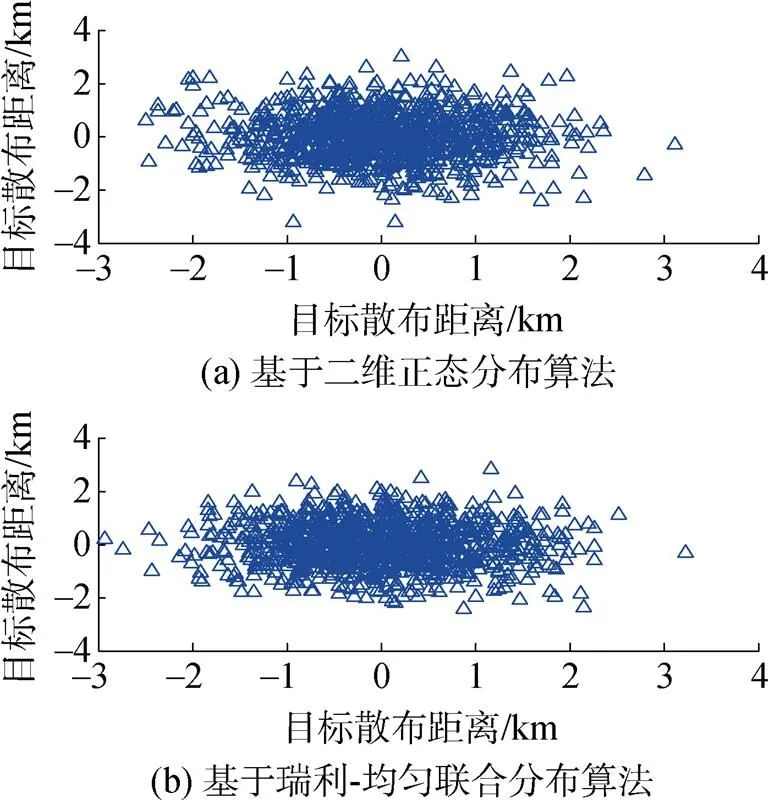
图 2 直角坐标系下目标初始位置散布区域
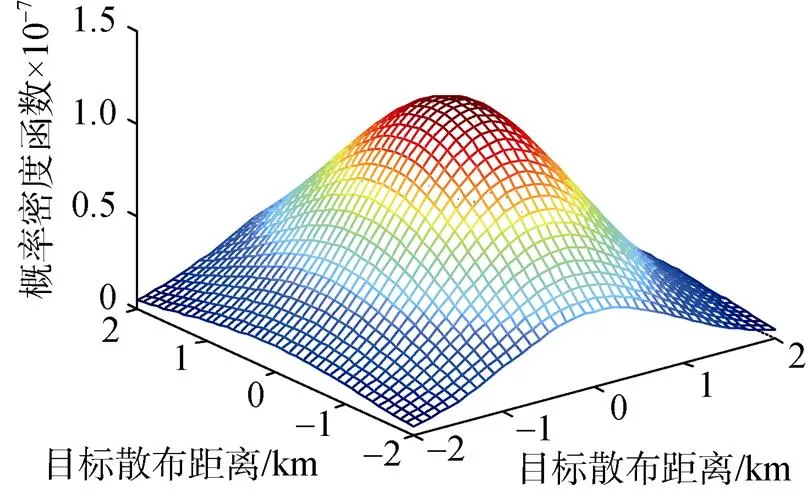
图3 基于二维正态分布的目标瞬时位置散布概率密度函数
基于瑞利-均匀联合分布的目标位置动态散布, 依据对目标速度的概略估计获得方差和概率密度函数。分别根据式(1)和式(7), 在直角坐标系下绘制t=30 min时的目标位置散布如图4所示。
由仿真结果可以看出, 2种算法计算结果不一致。进一步将2种算法仿真结果与蒙特卡洛法统计目标散布规律对比: 基于瑞利-均匀联合分布估计目标瞬时位置的散布区域与蒙特卡洛法统计的目标散布区域近似完全重合; 基于二维联合正态分布估计目标瞬时位置的散布区域不能覆盖蒙特卡洛法统计的目标散布区域。因此可知, 在目标速度、航向均未知的情况下, 基于瑞利-均匀联合分布估计目标瞬时位置的算法更为合理且符合战场实际。

图4 速度和航向未知时2种算法目标散布区域对比
获知目标速度时, 分别根据式(1)和式(8), 在直角坐标系下绘制t=30 min时刻的目标位置散布如图5所示。
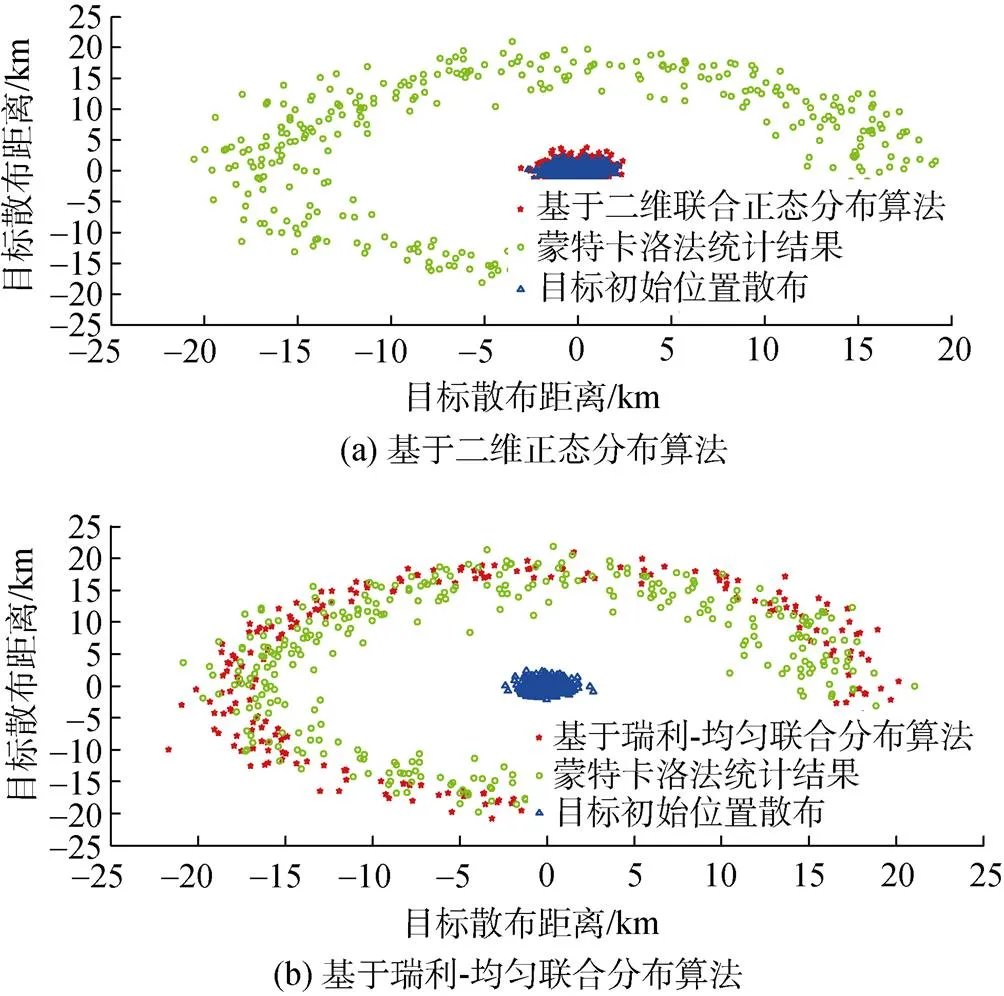
图5 速度已知、航向未知时2种算法目标位置散布区域对比
由仿真结果可以看出, 2种算法计算结果不一致。可知在目标速度已知、航向未知情况下, 基于瑞利-均匀联合分布估计目标瞬时位置的算法更为合理且符合战场实际。
4) 目标速度和航向均已知
获知目标速度和航向时, 分别根据式(1)和式(10), 在直角坐标系下绘制t=30 min时的目标位置散布如图6所示。
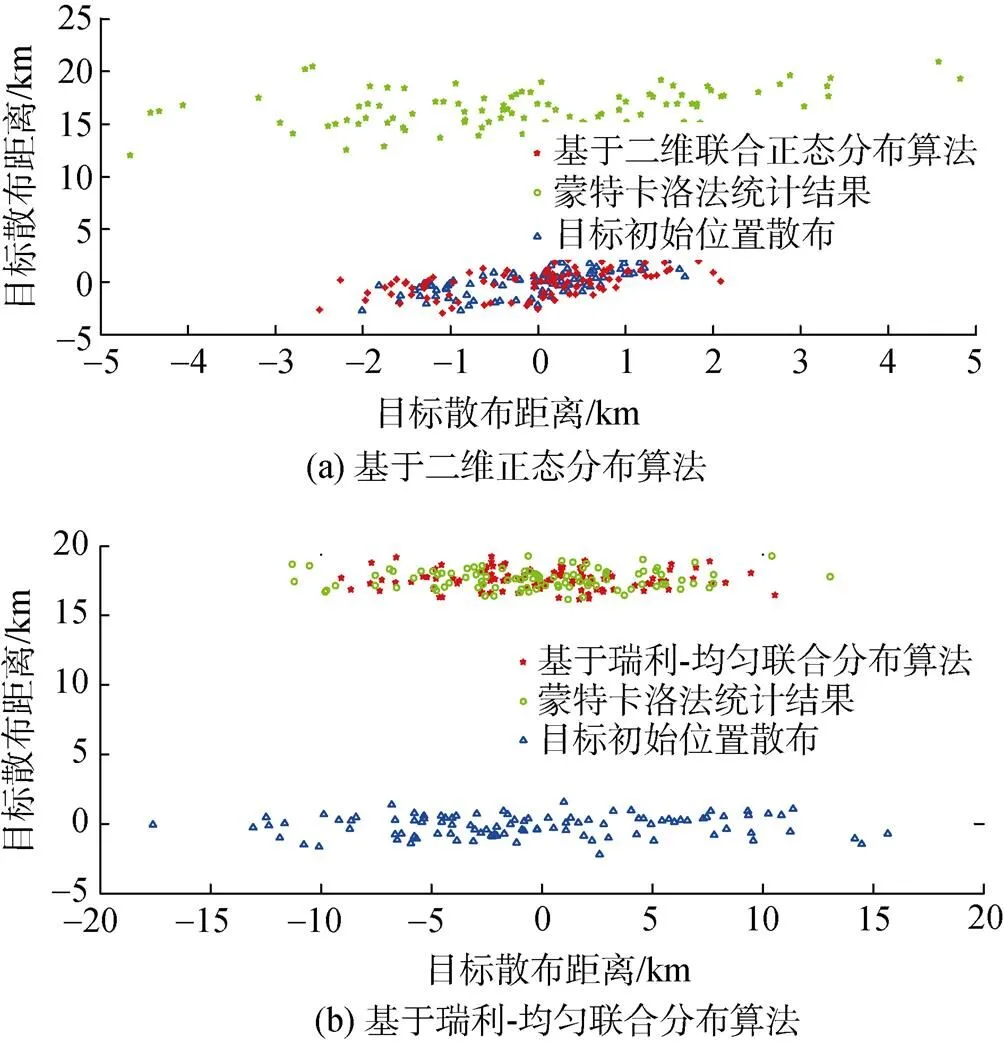
图6 速度和航向已知时2种算法目标位置散布区域对比
由仿真结果可以看出, 2种算法计算结果不一致。可知在目标速度和航向均已知的情况下, 基于瑞利-均匀联合分布估计目标瞬时位置的算法更为合理且符合战场实际。
3 结束语
文中提出了基于瑞利-均匀联合分布的目标散布估计方法, 该方法较目前工程应用中常用的基于二维正态分布的目标散布估计方法, 对运动目标的估计更为准确。
在应用中, 最常见的任务背景是AUV导航和航路规划中已知目标的概略速度和航向, 需估计目标瞬时位置散布的情况, 但目前各种文献提出的估计算法对此未详细分析, 或者是估计目标散布与实际目标散布误差过大, 文中方法在一定程度上填补了此应用情况的空白。
[1] 陈小龙. AUV水下地形匹配辅助导航技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
[2] Nygren I. Terrain Navigation for Underwater Vehicles[D]. Sweden: Signal Processing Stockholm, 2005.
[3] Xie Ying-rong. Terrain and Navigation[D]. Sweden: Sto- ckholm, 2005.
[4] 王汝鹏. 水下地形匹配定位置信区间估计[J]. 武汉大学学报(信息科学版), 2019, 44(6): 830-836.
Wang Ru-peng. Confidence Interval Estimation of Underwater Terrain Aided Position[J]. Geomatics and Infor- mation Science of Wuhan University, 2019, 44(6): 830- 836.
[5] 屈也频. 反潜飞机搜索效能评估与决策建模[M]. 北京: 国防工业出版社, 2010: 32-49.
[6] 徐梁, 牛庆功. 应召搜索中潜艇位置散布分析[J]. 水雷战与舰船防护, 2017, 25(1): 66-68.
Xu Liang, Niu Qing-gong. Analysis on Position Diffusion of Submarine in Call Search[J]. Mine Warfare & Ship Self-Defence, 2017, 25(1): 66-68.
[7] 陆明华, 赵琳. 潜艇指挥决策控制模型及仿真研究[J]. 舰船工程, 2005, 27(3): 60-63.
Lu Ming-hua, Zhao Lin. Submarine Command Decision Control Model and Simulation Research[J]. Ship Engeneering, 2005, 27(3): 60-63.
[8] 黄文斌. 潜艇在水面目标位置散布概率密度的计算方法[J]. 火力指挥与控制, 2013, 38(8): 169-172.
Huang Wen-bin. Calculation Methods for Probability Density of Object Locating of Submarine[J]. 2013, 38(8): 169-172.
[9] 李长军. 基于正态分布的水面目标位置散布分析[J]. 信息工程大学学报. 2012, 13(6): 650-653.
Li Chang-jun. Research on Probability Density of Object Locating Based on Normal Distribution[J]. Journal of Information Engineering University, 2012, 13(6): 650- 653.
Method for Estimating the Target Distribution Area in AUV Call Search Based on a Rayleigh-uniform Distribution
CUI Dong-hua1, 2, JI Xiu-mei3, DAI Zhi-heng4, WANG Tuan-meng5
(1. 91054thUnit, Chinese People’s Liberation Army, Beijing 443500, China; 2. School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China; 3. 31002thUnit, Chinese People’s Liberation Army, Beijing 443500, China; 4. The 716 Research Institute, China State Shipbuilding Corporation Limited, Lianyungang 222006, China; 4. The 705 Research Institute, China State Shipbuilding Corporation Limited, Xi’an 710077, China)
In the process of autonomous undersea vehicle(AUV) call search, the distribution area of the target is an important basis for guiding the platform for AUV path planning. Error distributions produced from the initial position and motion parameters of the target of information acquisition cause the position distribution function of the target to exhibit the characteristics of a non-normal, nonuniform distribution at any moment. However, the existing methods are often considerably simple or even unreasonable for describing the problem, resulting in phenomena that are inconsistent with reality. To solve the problem of estimating the target distribution area in an AUV call search, based on the estimation model of the target initial position distribution area, a Rayleigh-uniform joint estimation model is established according to the error distribution rules, such as target velocity and navigation. The simulation results show that the proposed method is more reasonable and practical than the traditional two-dimensional normal distribution method, providing a more accurate estimation of the target distribution area and facilitating convenient numerical analysis and engineering applications.
autonomous undersea vehicle(AUV); call search; target distribution area; Rayleigh-uniform joint estimation
崔东华, 纪秀美, 代志恒, 等. 基于瑞利-均匀分布的AUV应召搜索目标散布区域估计方法[J]. 水下无人系统学报, 2021, 29(5): 580-585.
P229; TB71.2
A
2096-3920(2021)05-0580-06
10.11993/j.issn.2096-3920.2021.05.010
2020-06-05;
2020-08-18.
崔东华(1970-), 女, 研究员, 主要研究方向为舰载武器系统与运用工程.
(责任编辑: 陈 曦)
