双发回转体水下齐射流体动力特性数值仿真
2021-11-08施瑶,高山,潘光
施 瑶, 高 山, 潘 光
双发回转体水下齐射流体动力特性数值仿真
施 瑶, 高 山, 潘 光
(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 西北工业大学 无人水下运载技术重点实验室, 陕西 西安, 710072)
为研究双发回转体水下齐射过程流体动力演化特性, 基于均质多相流理论、标准RNG-模型、Singhal空化模型以及重叠网格技术, 建立三维双发回转体水下齐射模型, 开展不同发射速度下双发回转体非定常空泡与运动姿态演变过程数值仿真, 分析了典型工况下双发回转体齐射过程流场结构演变、运动特性以及齐射速度对其运动特性的影响。结果表明: 航行前期空泡发展至最大, 随着航行器向自由液面运动,空泡从其末端由下至上逐渐脱落, 并发生了溃灭现象; 由于齐射过程中流动干扰区域的存在, 双发回转体肩部空泡形态演变过程由不对称演变为对称状, 从而导致回转体质心先向内侧偏移, 随后不断向外侧偏移;随着齐射速度的增大, 回转体出筒时刻空泡长度不断增大, 其质心由内侧向外侧偏移的交点向后推迟, 同时偏转角度不断减小。此研究对水下齐射工程技术具有一定的借鉴意义。
双发回转体; 水下齐射; 空泡; 回射流; 水动力特性
0 引言
齐射是指依托水下移动发射平台将两发或多发航行器以一定发射空间间距在极短时间内连续弹射出水的过程。单筒多航行器水下齐射技术因具有储弹量多、攻击扇面大、易于实现饱和攻击等优势, 可极大提高航行器突防概率, 因此受到各军事强国的高度关注。然而, 在水下齐射过程中, 航行器肩部低压区会出现空化, 并伴随着生长、脱落以及溃灭等复杂非定常多相流现象, 加之齐射过程中, 航行器之间会产生较为严重的流动干扰现象, 导致其两侧非定常空化区域不对称演变, 直接影响其运动姿态的稳定性。
水下发射过程常常涉及大尺度空泡群非定常演化, 早期研究的单空泡相关理论成果难以直接应用[1-3]。因此, 国内外相关学者针对回转体水下发射过程非定常空泡特性与运动特性开展了相关研究。Dyment等[4]基于雷诺平均方程(Reynolds averaged Navier-Stokes, RANS)方法和流体体积(volume of fluid, VOF)多相流模型对回转体出水过程的尾空泡进行数值仿真, 仿真结果与相关实验吻合度良好; 王一伟等[5-6]针对回转体水下发射过程中空泡生成、发展、脱落和溃灭等开展了系统研究, 给出了将回射流运动时间与回转体运动时间比值作为空泡稳定性的重要判据; 魏英杰等[7]将质量输运空化模型与混合介质RANS方法相结合, 给出了回转体阻力系数和空化数之间的关系, 分析了肩空泡对回转体流体动力特性的影响。权晓波等[8]采用MIXTURE多相流模型与动网格技术对回转体水下发射过程进行了计算, 获得了尾空泡生成演化的周期性特征, 同时发现了发射水深增加导致尾空泡压力增大的现象。
回转体水下齐射涉及多体间流动干扰的水动力问题, 由于此概念较新, 相关文献较少, 但可以借鉴多体在无固壁干扰条件下相互干扰的相关研究成果[9-10]。何春涛[11]对2个并联圆柱体入水进行了数值仿真, 分析了空泡内部轮廓的演变过程, 给出了双体入水过程中流动干扰消失的临界发射间距。宋武超等[12]基于势流理论和非线性假设, 引入二维轴对称入水空泡计算模型和影响函数, 给出了双体并联入水过程空泡的三维演化特性。Xu等[13]研究了双发回转体以不同时序出水过程, 发现当反向旋转涡对出现时, 对次发回转体的运动姿态产生较大的影响。
综上可知, 关于水下垂直发射过程中非定常空泡演化与出水弹道特性的研究主要集中在单发航行器, 而针对航行器水下齐射过程, 应重点关注流动干扰条件下航行器肩部空泡非定常演化与出水弹道特性, 但目前针对该问题的研究有限。因此, 文中通过开展三维双发回转体水下齐射过程水动力特性数值仿真, 获取非定常空泡脱落及溃灭过程中回转体运动特性的演变规律, 此研究对后续水下齐射工程技术具有一定的借鉴意义。
1 数值计算方法
1.1 控制方程
描述回转体水下垂直发射气液多相流动的基本控制方程包括连续性方程、动量方程和能量方程, 其基本形式如下。
连续性方程
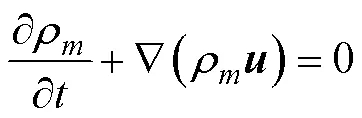
动量方程

能量方程

1.2 湍流方程
采用标准RNG-模型, 通过修正湍流黏度, 并考虑了平均流动中的旋转和旋流流动情况, 能够更好地处理高应变率以及流线弯曲程度较大的流动。
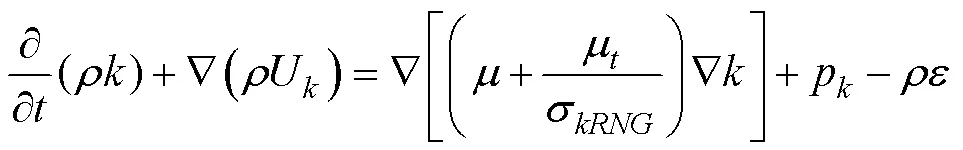

其中, 湍流黏性
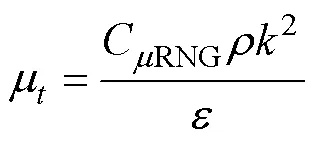
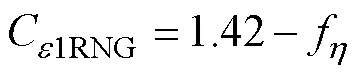
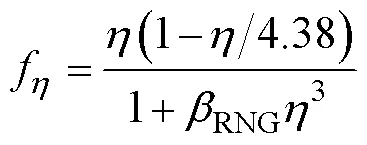
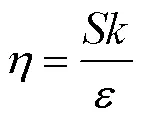

1.3 空化模型
采用Singhal空化模型, 其计算公式如下
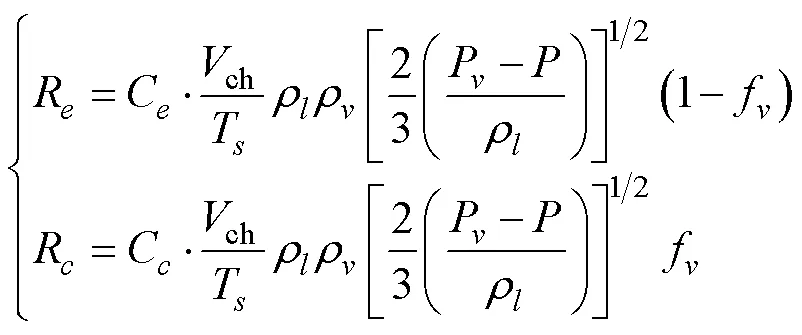
上式包含的假设有:
1) 不考虑韦伯数的变化, 将其视为经验系数;
2) 速度与相变率呈线性关系;
当地压力小于空化压力, 即<p时, 空化率为
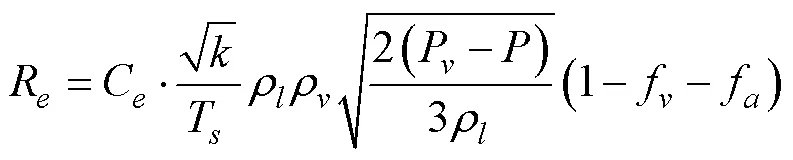
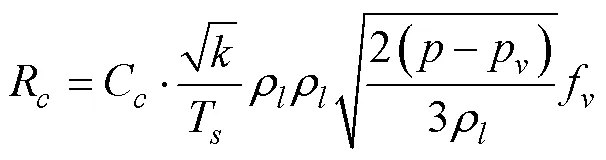
式中, 经验参数取值为C=0.02,C=0.02。
1.4 VOF多相流模型
VOF多相流模型是一种在固定Euler网格下的表面跟踪方法, 它适用于在能够解决混合物各相之间界面的数值网格上模拟多种互不相容流体的流动。文中求解的气-液-汽3相流动问题中, 液相为主相, 其余2相为次相。如图1所示, 若液相体积分数为, 气相体积分数为, 汽相体积分数为, 则混合相体积分数为1---。
1.5 重叠网格技术
重叠网格的节点分为洞内点、计算点和插值点3种。洞内点不参与流场计算, 计算点参与流体计算, 插值点进行流场信息的传递, 3种网格节点在重叠网格分布如图2所示。

图1 VOF模型原理示意图
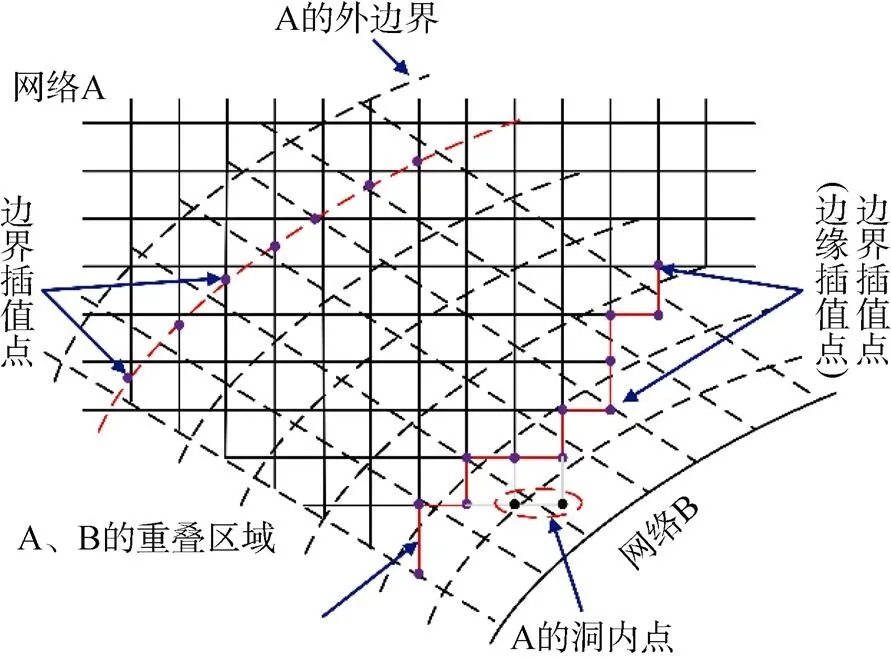
图2 重叠网格示意图
重叠网格技术的基本思想是利用子域网格在重叠区域进行插值处理实现流场信息的实时传递, 解决了传统贴体网格重组过程带来的网格畸变等问题。重叠网格的实现流程包括网格生成、网格装配、数值计算、网格更新直至求解完成全过程, 具体的实现流程如图3所示。
2 数值计算模型
2.1 几何模型与网格划分
首先建立双发回转体水下齐射模型, 其中模型直径=15 mm, 长细比/=10,为回转体长度, 采用半球头型。考虑到文中研究双发回转体水下齐射流动干扰过程, 为了控制计算量和提高计算效率, 截取1/2双发回转体水下齐射流场计算域开展数值计算, 如图4所示。
图5为回转体模型网格划分, 为了更好捕捉回转体周围流场细节演变, 对发射筒口、筒口上方流域以及自由液面进行了局部加密, 其中第1层网格高度为0.045 mm, 所对应的+为40; 为更好地节约计算资源, 在远场设置较大网格尺度。

图5 模型网格划分
2.2 数值算法与网格无关性验证
为了验证数值仿真方法的有效性, 基于上述数值计算方法的建立及边界条件设置, 文中自主设计了回转体水下发射试验装置, 并对单发回转体水下垂直发射过程开展实验与数值计算对比分析。图6所示为回转体水下发射实验平台示意图, 主要由发射系统、控制系统, 高速摄像系统以及防护回收系统组成。发射装置由储气瓶、减速电机、水下导轨、发射筒及各种线路等组成, 通过控制系统调节储气瓶气压大小来使航行器达到所需的出筒速度; 高速摄像系统由控制电脑、Phantom型号高速摄像机及相应线路等组成。调节高速摄像机的白平衡、分辨率(640×1 024)、帧率(3000帧/s)及曝光时间等参数, 以拍到清晰的画面; 实验中选用2盏1 000 W和2盏500 W新闻灯作为背景光源, 以保证摄像视野清晰。防护回收系统由泡沫防护板、起吊装置等组成。实验中采用泡沫防护板来抵消航行器出水惯性载荷的冲击, 既保证了实验人员的安全性, 同时又防止航行器头型损坏。此外, 仿真和实验缩比模型为1:1, 初始条件设置一致。
图7和图8分别给出了仿真计算与试验相图对比和竖直方向位移对比。从图中可以发现, 水下运动阶段, 仿真结果和试验结果数据吻合度较好, 包括尾空泡演变以及数值方向弹道。试验中尾空泡由于发射筒口不均匀气团效应导致回射流产生, 与仿真存在一定的误差, 竖直方向弹道在出水阶段最大有7.2%的误差。误差来源主要是试验数据提取误差以及出水喷溅造成的误差, 可以认为此仿真方法达到了要求的精度。
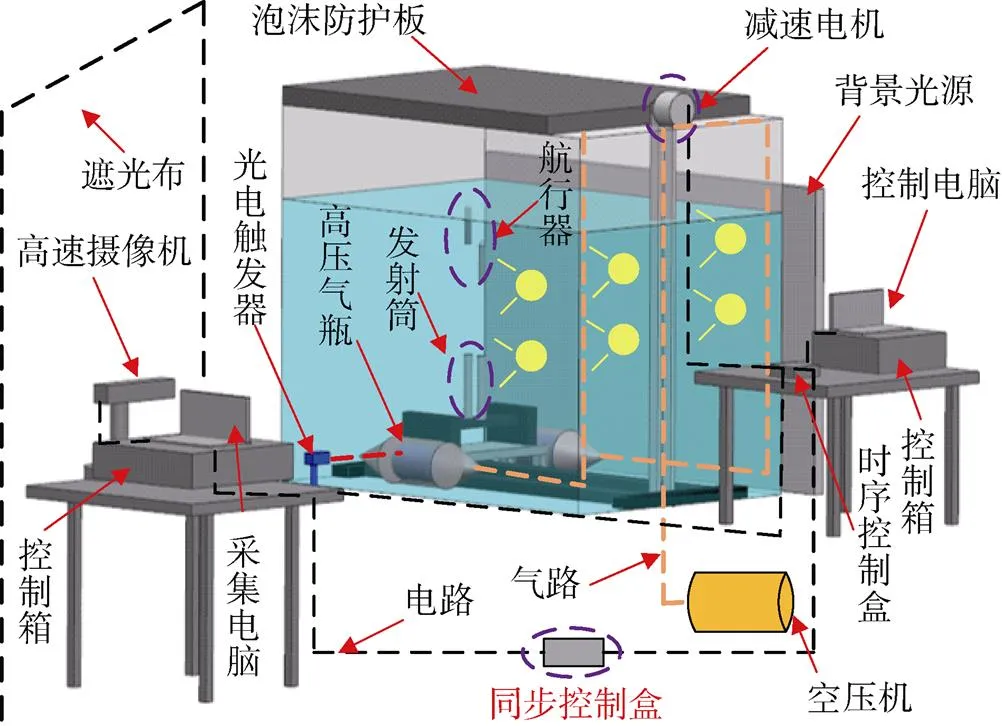
图6 水下垂直发射试验系统示意图

图7 仿真计算与实验相图对比

图8 竖直方向位移对比
针对上述回转体模型, 开展了粗糙尺度网格(2.37×106)、中等尺度网格(4.05×106)与精细尺度网格(6.13×106)计算结果对比, 不同尺度网格计算下回转体竖直方向位移演变如图9所示。
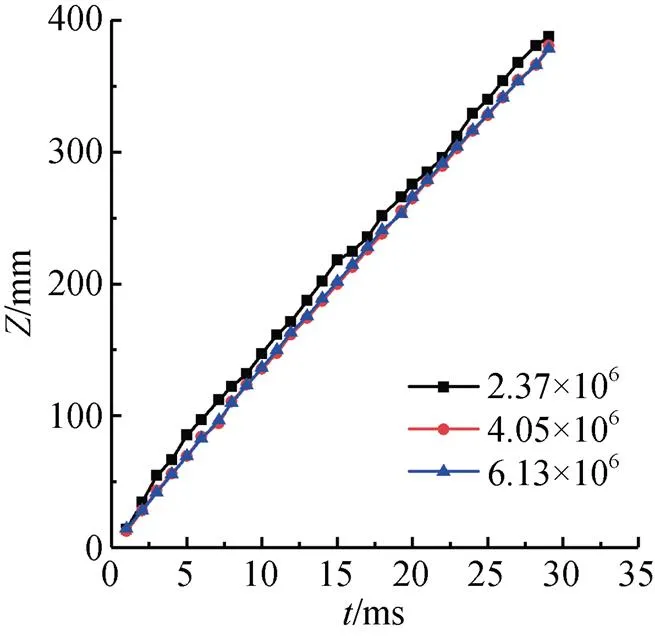
图9 网格无关性验证
从图9中可以看出粗糙尺度网格计算结果与中等、精细尺度网格差异较大, 而中等尺度网格与精细尺度网格计算结果基本一致。考虑到计算成本和效率, 故选取中等尺度网格(4.05×106)开展数值计算, 满足重叠网格计算要求。
3 仿真结果与分析
3.1 流场结构演变
图10为典型工况下速度为18 m/s时双发回转体水下齐射液相体积分数演变云图。由图可知,当回转体尾端完全出筒时, 其速度达到最大值, 此时空化数最小, 回转体肩部低压区空泡发展最长。后期随着回转体不断向自由液面运动, 速度不断减小, 空化数增大, 空泡沿着其末端向回转体头部方向不断脱落直至消失。图11为双发回转体水下齐射压力演变云图。由图可知, 双发回转体附近的压力分布基本一致, 其中回转体对流场压力的影响主要集中在头部和尾部驻点附近的高压区, 其中尾端驻点附近高压区形成主要原因如下: 当周围流体沿回转体头部区域运动至尾端区域时, 由于惯性作用, 运动流体在失去回转体几何表面的约束后, 会呈一定角度向回转体尾端中心线位置靠拢, 此角度与回转体几何形状以及速度密切相关; 当两股流体在尾端汇合时, 速度方向一致的流体分子将会相互叠加, 速度方向相反的流体分子将会发生激烈碰撞, 从而造成尾端驻点高压区的形成。
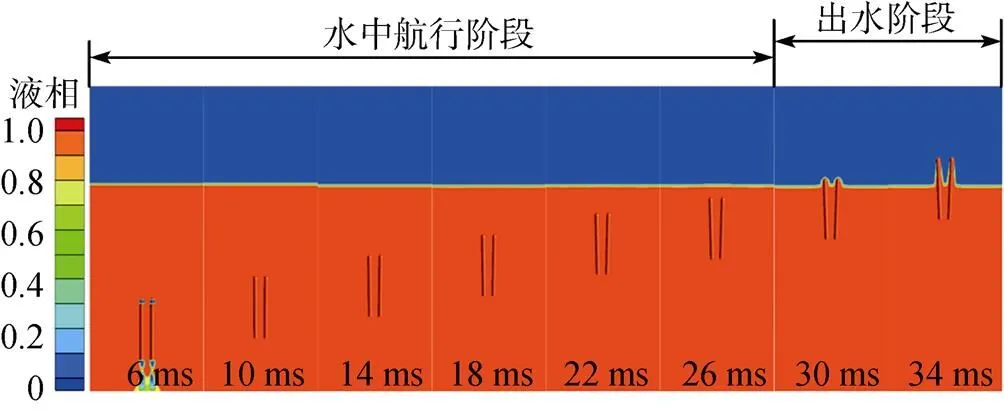
图10 双发回转体水下齐射液相体积分数演变云图
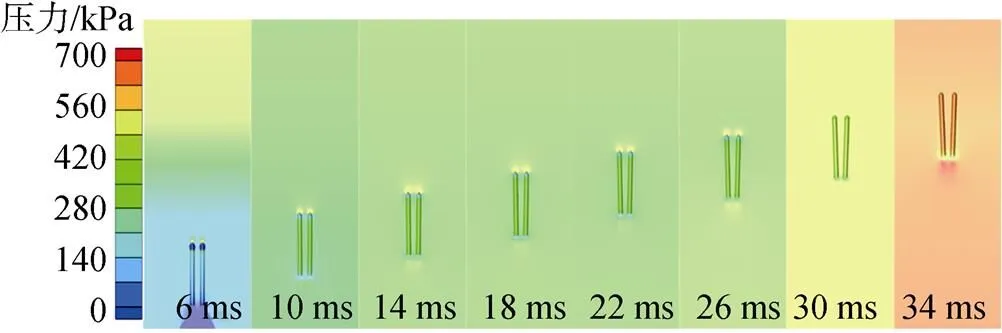
图11 双发回转体水下齐射压力演变云图
图12和图13分别给出了典型时刻回转体空泡压力与形态演变。从图中可以发现, 双发回转体初期空泡末端出现了明显的不对称逆压梯度, 导致空泡末端形态发生不对称演变。由于空泡从其末端开始溃灭, 以致其末端近似驻点位置压力较高, 加之回转体之间流动干扰区域的影响, 空泡末端两侧驻点位置与空泡内部低压区共同形成较高的逆压梯度, 此逆压梯度与航行器轴线之间的夹角小于90°, 形成不对称逆压梯度。同时在不对称逆压梯度的影响下, 产生不对称回射流, 如图14所示为8 ms流线图。

图12 典型时刻回转体空泡压力演变
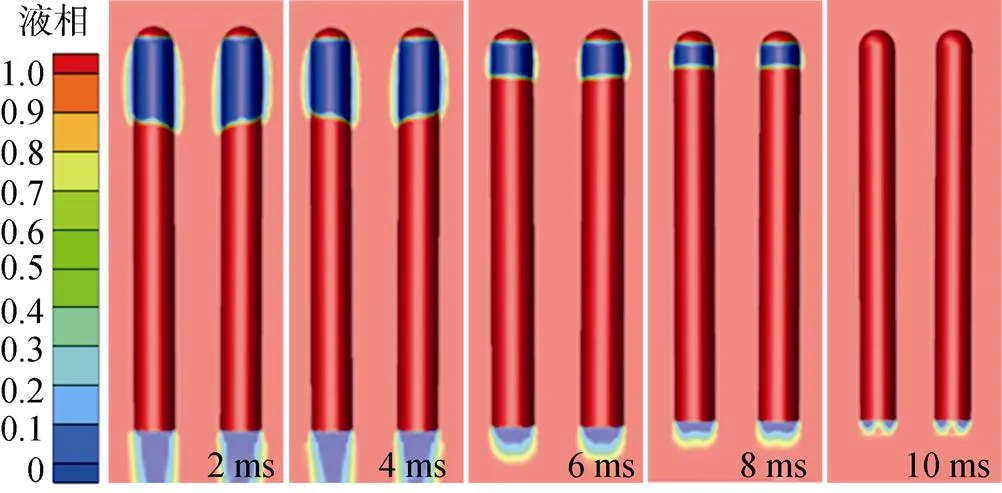
图13 空泡形态演变图
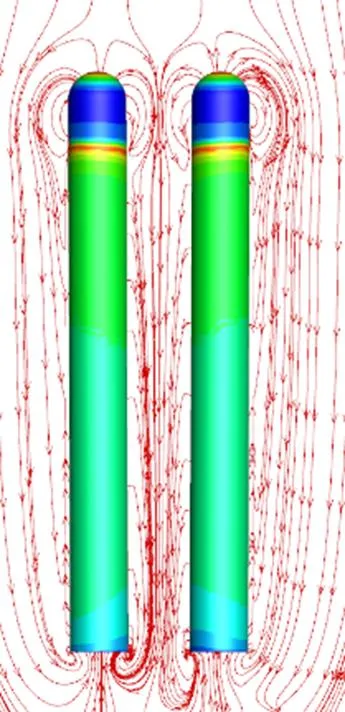
图14 8 ms流线图
随着航行器向自由液面运动, 不对称回射流沿着空泡末端两侧不断向其头部方向运动, 并伴随着空泡脱落及溃灭现象; 整个过程中, 随着航行器运动姿态的演变, 回射流由不对称发展成对称状, 最后空泡发生溃灭现象, 对回转体运动姿态的稳定性产生了较大影响。
3.2 回转体运动特性
定义回转体在水中航行初始状态为0时刻, 偏转角逆时针为正。如图15所示为双发回转体在轴方向上的速度和位移曲线, 可以发现双发回转体运动特性基本一致, 在运动过程中双发回转体质心首先向内侧偏转约0.6 mm, 随后不断向外侧偏转约2 mm。根据速度曲线可知, 双发回转体质心后续相互远离趋势增大。
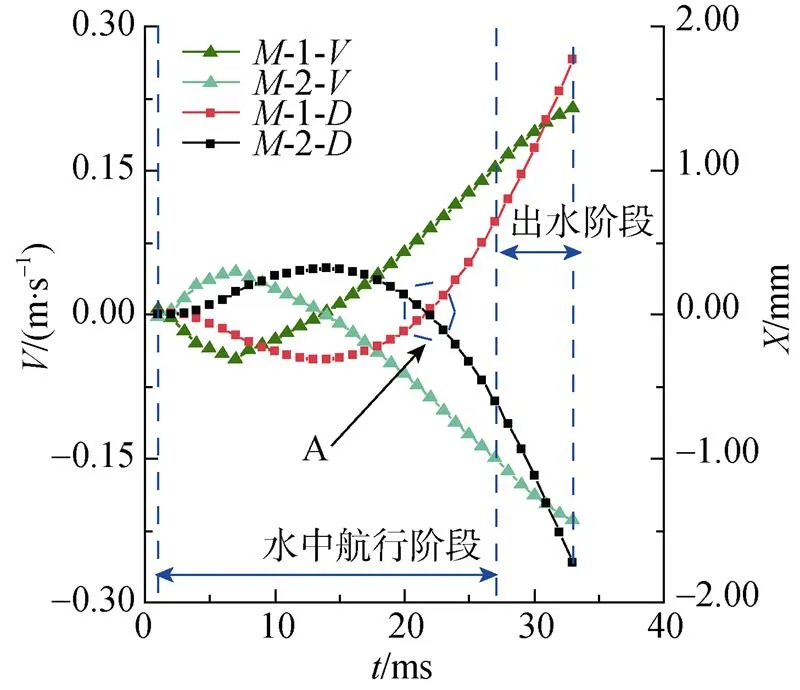
图15 X轴方向速度与位移曲线
航行器水下航行阶段, 局部当地空化数在非定常空泡的演变过程中, 可以表示为
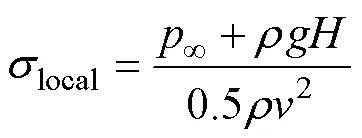
航行器垂直向自由液面运动过程中, 由于空化数与速度的二次方成反比, 如图15所示, 随着航行器速度减小, 空化数急剧增大, 导致航行器末端空泡发生脱落及溃灭现象。基于此, 针对齐射过程航行器肩部空化现象展开数值分析。
图16和17分别为回转体在轴方向上的受力以及沿轴方向的偏转力矩曲线。从图中可知, 在水中航行前期, 左侧回转体所受合力为负, 指向其内侧; 右侧回转体所受合力为正, 也指向其内侧。而左侧回转体偏转力矩为正, 沿逆时针方向; 右侧回转体偏转力矩为负, 沿顺时针方向, 故而回转体此过程中所受的合力作用点在质心以下区域。此外, 双发回转体受到向外侧的合力逐渐减小, 导致其横向速度增大趋势有所减小。但由于此时偏转力矩不断增大, 回转体向外侧偏转的角度不断增大, 伴随着回转体出水, 头部迎流作用消失, 偏转力矩消失, 偏转角度此时达到最大, 如图18所示。
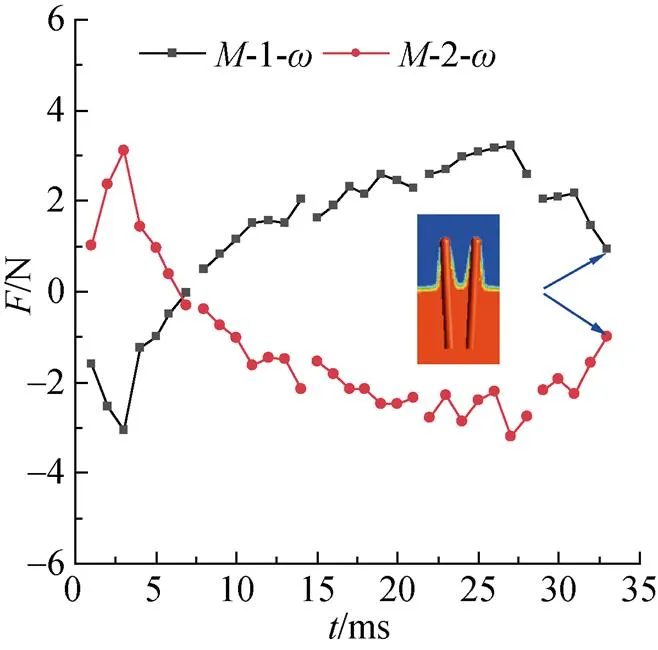
图16 X轴方向受力曲线
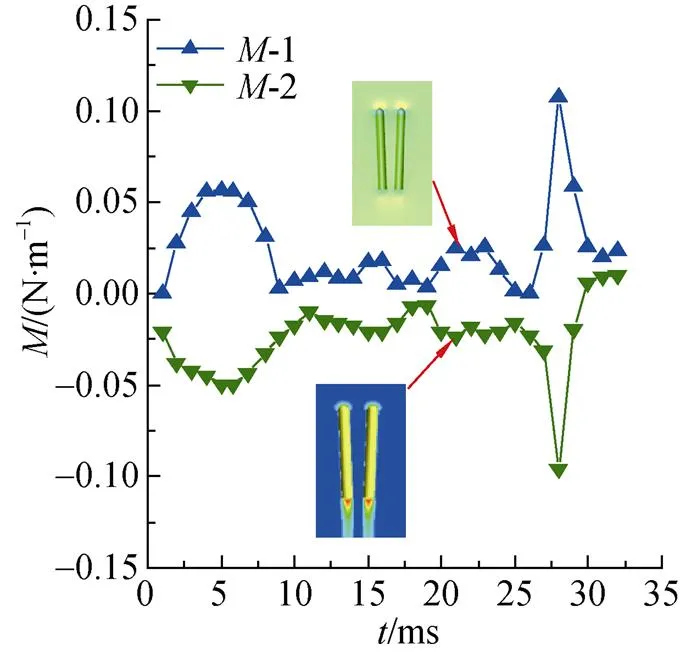
图17 Y轴方向力矩曲线
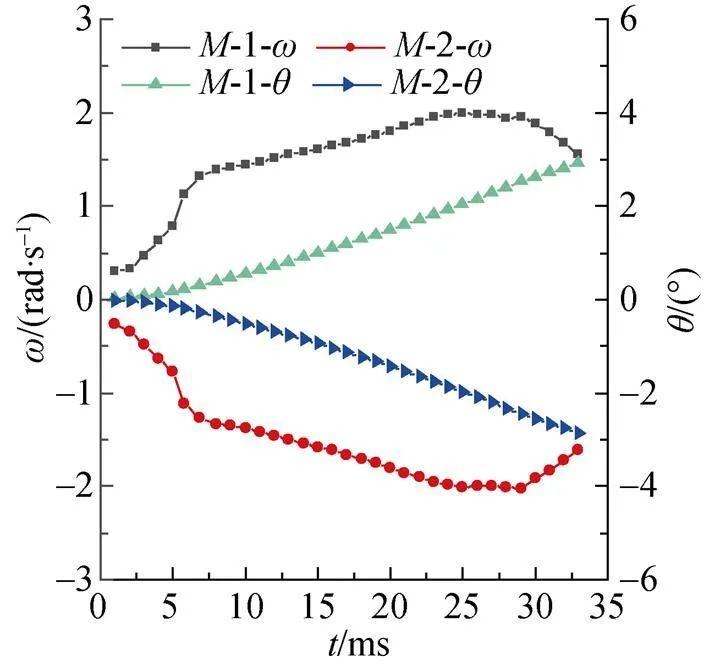
图18 偏转角速度和偏转角曲线
结合回转体空泡形态具体说明, 图19为典型时刻回转体空泡形态与受力图, 由于空泡的不对称性, 导致回转体质心偏上区域外侧沾湿面积较大, 此时均布力所产生的均布力矩M如图所示, 加之合力作用于质心以下, 回转体在此力矩的作用下向外侧偏转, 这与回转体偏转角演变曲线一致。随着双发回转体都不断向外侧偏转, 外侧区域演变为背流侧, 内侧区域演变为迎流侧。因此, 相比回转体背流侧区域, 其迎流侧空泡脱落速度较快, 导致空泡两侧由不对称向对称状转变, 直至发生溃灭现象, 如图20所示。
3.3 发射速度对运动特性影响分析
图21与图22分别为不同发射速度(14、16、18 m/s)下回转体水下齐射弹道及偏转角曲线。由图21可知, 随着发射速度的增加, 双发回转体质心向外侧偏移点不断推迟, 偏转角度不断减小。随着回转体尾端出筒速度的增加, 空化数减小, 空泡发展更长。因此, 齐射速度18 m/s时空泡长度最大, 其空泡溃灭时间相比齐射速度14m/s和16m/s推迟, 导致水中航行阶段横向受力方向由内侧向外侧转变交点推迟。
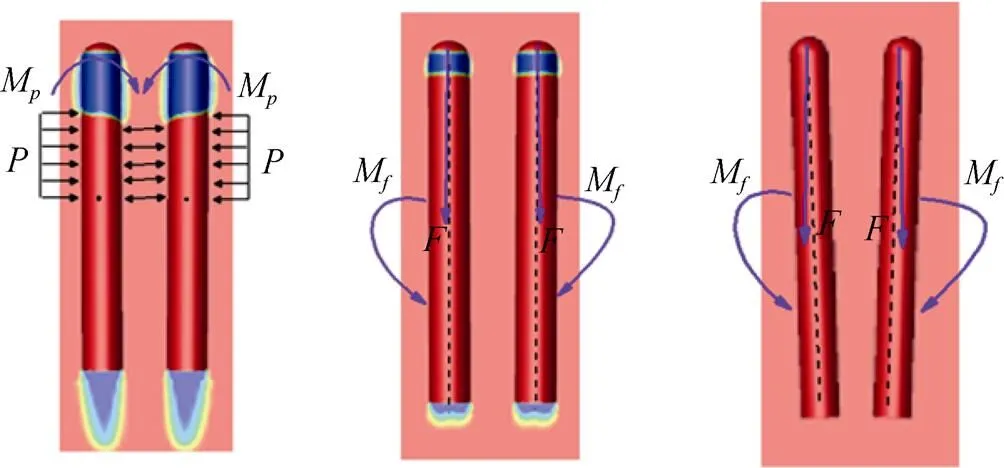
图19 双发回转体空泡演化与受力图
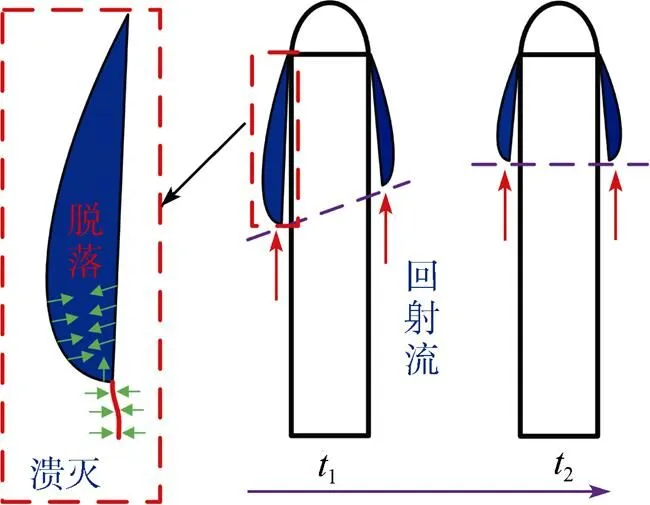
图20 不对称空泡脱落示意图
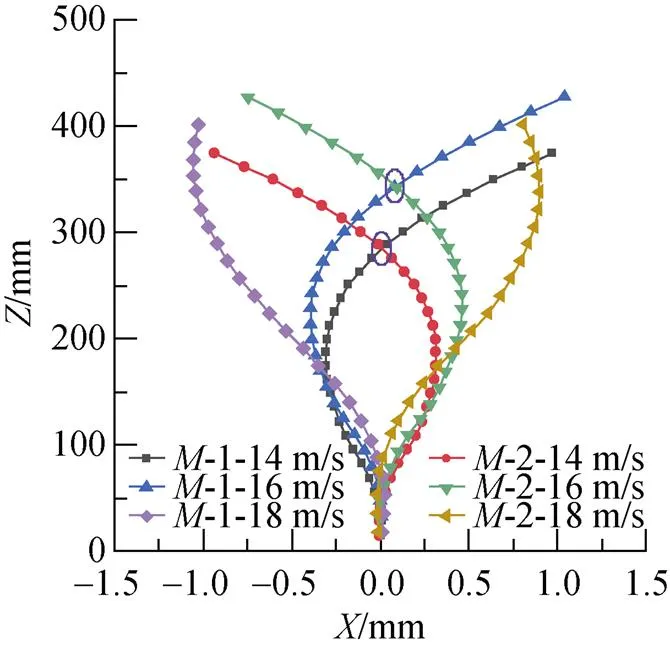
图21 双发回转体水下齐射弹道曲线
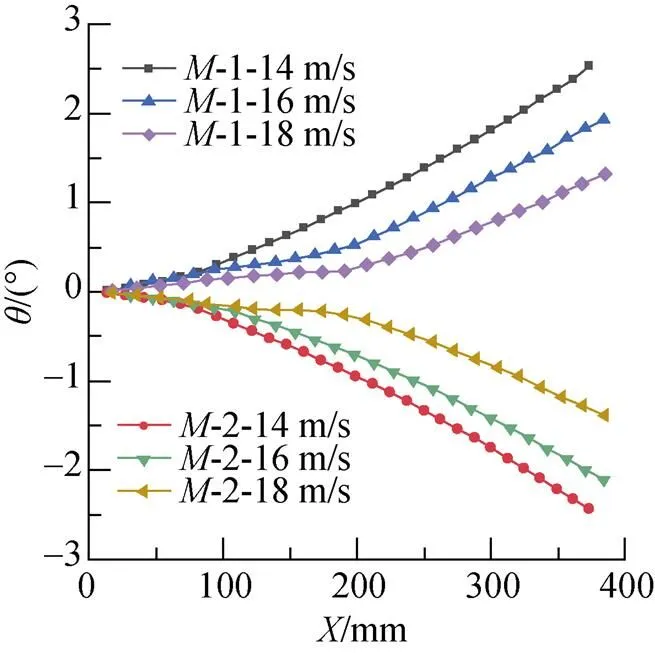
图22 双发回转体偏转角度曲线
此外, 随着发射速度的增加, 回转体在相同水深条件下的航行时间越短, 加之偏转力矩方向不变, 导致偏转角度不断减小, 如图22所示。因此基于上述分析, 可通过流动控制手段, 如被动排气, 来改变航行器肩部附近压力分布特性, 或采用抗空化头型来抑制空化现象的产生, 从而提高航行器运动姿态的稳定性。
4 结论
基于均质多相流理论、标准RNG-模型、Singhal空化模型以及重叠网格技术, 建立了三维双发回转体水下齐射数值计算模型, 模拟了不同齐射速度下回转体运动特性演变过程, 获得以下结论。
1) 回转体出筒时刻, 其发射速度达到最大值, 空化数最小, 导致空泡长度最大; 随着回转体不断向自由液面运动, 其肩部空泡在回射流的作用下从其末端由下至上逐渐脱落, 并发生溃灭现象。
2) 水中航行阶段, 由于齐射过程狭长流动干扰区域的存在, 双发回转体肩部空泡形态从不对称状演变为对称状, 导致双发回转体横向受力在航行初期方向发生变化, 偏转力矩方向不变, 从而其质心先向内偏移随后向外偏移。
3) 回转体齐射速度越大, 出筒时刻空泡长度越长, 其质心由内侧向外侧偏移的交点越向后推迟; 而回转体所受偏转力矩方向不变, 导致偏转角度不断减小。
[1] Plesset M S, Chapman R B. Collapse of an Initially Spherical Vapour Cavity in the Neighbourhood of a Solid Boundary[J]. Journal of Fluid Mechanics, 1971, 47(2): 283-290.
[2] Plesset M S, Prosperetti A. Bubble Dynamics and Cavitation[J]. Annual Review of Fluid Mechanics, 1977, 9(1): 145-185.
[3] Brennen C E. Cavitation and Bubble Dynamics[M]. Oxford, UK: Oxford University Press, 1995.
[4] Dyment A, Flodrops J P, Paquet J B, et al. Gaseous Cavity at the Base of an Underwater Projectile[J]. Aerospace ence & Technology, 1998, 2(8): 489-504.
[5] 王一伟, 黄晨光, 吴小翠, 等. 航行体水下垂直发射空泡脱落条件研究[J]. 工程力学, 2015, 32(11): 33-39.
Wang Yi-wei, Huang Chen-guang, Wu Xiao-cui, et al. Investigation of Cavities Shedding Condition on Underwater Vehicles in the Vertical Launch Process[J]. Engineering Mechanics, 2015, 32(4): 544-550.
[6] 王一伟, 黄晨光, 杜特专, 等. 航行体垂直出水载荷与空泡溃灭机理分析[J]. 力学学报, 2012, 44(1): 39-48.
Wang Yi-wei, Huang Chen-guang, Du Te-zhuan, et al. Mechanism Analysis about Cavitation collapse Load of Underwater Vehicles in a Vertical Launching Process[J]. Chinese Journal of Theoretical and Applied Mechanics. 2012, 44(1): 39-48.
[7] 魏英杰, 闵景新, 王聪, 等. 潜射导弹垂直发射过程空化特性研究[J]. 工程力学, 2009, 26(7): 251-256.
Wei Ying-jie, Min Jing-xin, Wang Cong, et al. Research on Cavitation of Vertical Launch Submarine Missile[J]. Engineering Mechanics, 2009, 26(7): 251-256.
[8] 权晓波, 燕国军, 李岩, 等. 水下航行体垂直发射尾空泡生成演化过程三维数值研究[J]. 船舶力学, 2014(7): 739-745.
Quan Xiao-bo, Yan Guo-jun, Li Yan, et al. Three-dimensional Numerical Study on the Evolution Process of Tail Bubble of Underwater Vehicle Vertical Launching[J]. Journal of Ship Mechanics, 2014(7): 739-745.
[9] 程丽, 张亮, 吴德铭, 等. 无升力双体水动力干扰计算[J]. 哈尔滨工程大学学报, 2005, 26(1): 1-6.
Cheng Li, Zhang Liang, Wu De-ming, et al. Hydrodynamic Interactions between Two Underwater Non-lifting Bodies[J]. Journal of Harbin Engineering University, 2005, 26(1): 1-6.
[10] 金大桥, 王聪, 魏英杰, 等. 水下轴向串列双圆柱体带空泡绕流研究[J]. 哈尔滨工程大学学报, 2010, 31(10): 1329-1334.
Jin Da-qiao, Wang Cong, Wei Ying-jie, et al. Cavitating Flow Study of an Underwater Two Axial Circular Cylinder in Tandem Arrangement[J]. Journal of Harbin Engineering University, 2010, 31(10): 1329-1334.
[11] 何春涛. 典型运动体入水过程多相流动特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
[12] 宋武超, 魏英杰, 路丽睿, 等. 基于势流理论的回转体并联入水双空泡演化动力学研究[J]. 物理学报, 2018, 67(22): 240-256.
Song Wu-chao, Wei Ying-jie, Lu Li-rui, et al. Dynamic Characteristics of Parallel Water-entry Cavity Based on Potential Flow Theory[J]. Acta Physica Sinica, 2018, 67(22): 240-256.
[13] Xu H, Wei Y, Wang C, et al. On Wake Vortex Encounter of Axial-symmetric Projectiles Launched Successively Underwater[J]. Ocean Engineering, 2019, 189: 106382.1- 106382.11.
Numerical Simulation of Hydrodynamic Characteristics of Double-Revolving Bodies in Underwater Salvo
SHI Yao, GAO Shan, PAN Guang
(1. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China; 2. Key Laboratory of Unmanned Underwater Vehicle Technology of Ministry of Industry and Information Technology, Xi’an 710072, China)
To study hydrodynamic characteristics in the underwater salvo process of double-revolving bodies, a three-dimensional underwater salvo model is built in this study based on the homogeneous multiphase flow theory, standard RNG-model, Singhal cavitation model, and overlapping mesh technique. Numerical simulations of the evolution of an unsteady cavity are conducted to determine themovement attitudes of double-revolving bodies at different launching velocities. The flow structure evolution, motion characteristics, and salvo velocity during the salvo process under a typical condition are analyzed. The results show that the maximum development of the cavity is observed during the early stage of water navigation. As the revolving bodies move towards the free surface, the cavity gradually sheds from its end towards its top. The structure collapses owing to a flow interference region in the salvo process, because the evolution of the cavity in the shoulder of the double-revolving bodies is from asymmetric to symmetric, causing mass center deflection of the revolving bodies from the inside to the outside. As the salvo velocity increases, the length of the cavity increases at the outlet of the tube moment, the intersection point of the deflection of the center of mass from the inside to the outside is delayed backward, and the angle of deflection decreases.
double-revolving bodies; underwater salvo; cavity; hydrodynamic characteristic
施瑶, 高山, 潘光. 双发回转体水下齐射流体动力特性数值仿真[J]. 水下无人系统学报, 2021, 29(5): 524-532.
TJ630.1; O351.2
A
2096-3920(2021)05-0524-09
10.11993/j.issn.2096-3920.2021.05.003
2020-11-05;
2020-12-09.
国家自然科学基金(52172324); 中央高校基本科研业务费(3102019JC006).
施 瑶(1988-), 男, 博士, 副研究员, 主要研究方向为水下发射水动力学.
(责任编辑: 许 妍)
